半解析衛星軌道不確定性快速估計方法

于彥君，岳程斐，李化義，陳雪芹，劉培

（1.哈爾濱工業大學衛星技術研究所，哈爾濱 150001；2.哈爾濱工業大學（深圳）空間科學與應用技術研究院，深圳 518055；3.上海衛星工程研究所，上海 710119）

0 引言

軌道不確定性傳播是指在給定軌道初始狀態及其相關不確定性的基礎上，預測未來的軌道狀態及其統計特性。軌道不確定性傳播在空間態勢感知與決策等相關任務中起著重要作用，例如軌跡跟蹤、碰撞概率分析、傳感器資源管理和異常檢測等［1］。對于航天器而言，其軌道狀態矢量的真值是無法確切知道的，當存在測量信息時，軌道狀態誤差可以通過濾波算法［2］進行估計，該過程通常是收斂的；當不存在測量信息時，可利用濾波算法的預測步驟進行不確定性估計，即進行軌道不確定性傳播，該過程通常是發散的。在軌道不確定性傳播問題中，初始軌道不確定性在任何坐標系中都不是絕對高斯的，但目前通常采用高斯假設。高斯誤差超橢圓體隨著傳播時間的增加而放大和旋轉，并且由于動力學的非線性性質而逐漸變為非高斯的。在笛卡爾坐標系中，非高斯軌道不確定性通常位于“香蕉型”弧線上，該弧線沿航天器的標稱軌跡彎曲［3］。軌道不確定性的典型傳播過程如圖1所示。

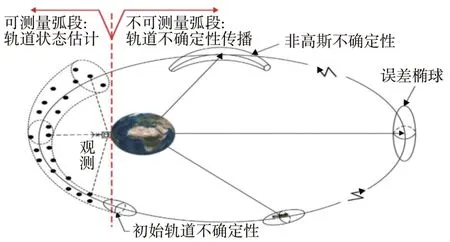
圖1 軌道不確定性傳播示意圖［1］Fig.1 Illustration of uncertainty propagation process［1］

軌道不確定性傳播方法包含局部線性化方法和蒙特卡洛法（Monte Carlo method，MC）等［4-5］。然而，由于軌道動力學的非線性特質，局部線性化方法過低的精度和蒙特卡洛方法的高計算量極大地阻礙了這2種方法的應用。為了在降低計算量的同時保證合適的精度，針對不同場景，學者們提出了多種適用于非線性軌道不確定性傳播的方法，例如高斯和模型（Gaussian mixture model，GMM）［6-7］、無跡變換法（Unscented transformation，UT）［8］、狀態轉移張量法［9］、微分代數法［10］、多項式展開法［11］、坐標轉換法［12-13］以及將上述方法相互結合的混合方法等［14-17］。在這些方法中，UT法［18］解決了線性化方法和蒙特卡洛法不能兼顧計算效率和精度這一難題。其通過非線性積分從初始分布中確定性地選擇樣本來近似未來時間的概率分布以取代復雜的高階分析。這一過程中，通過近似概率分布代替近似非線性變換，提高了計算精度；通過較少的樣本計算代替MC 法中的大樣本計算，提高了計算效率。坐標轉換法則通過選擇在非線性較弱的坐標系中建立動力學模型，在相同計算量條件下，達到大幅延長不確定性真實度（Uncertainty realism，UR）［19］保持時間的效果。坐標轉換法與UT 法相結合可用于軌道不確定性的傳播，如文獻［20］和［21］。

隨著低軌巨型衛星星座的發展，衛星間碰撞概率顯著增加，尤其當單顆衛星同時面臨與多個衛星碰撞的風險時，快速估計分析軌道不確定性傳播結果并評估碰撞風險成為亟待突破的問題。特別是考慮星上有限計算能力條件下，在確保不確定性估計精度的基礎上，快速獲得某一特定時刻或時段內的軌道狀態及其統計特性具有重要的應用價值。

針對這一問題，本文提出了一種基于半解析法的軌道不確定性估計方法。該方法是一種混合方法，具體特點如下：首先選擇在軌道要素坐標系中進行不確定性傳播，延長UR 的保持時間，跟蹤笛卡爾坐標系中非高斯形式的軌道不確定性。其次，采用解析模型結合迭代法實現對任意時刻的軌道要素的快速計算，并將該方法應用于軌道不確定性估計，大幅提升計算效率。此外，采用球形單邊采樣策略而非目前常用的對稱采樣策略，進一步降低由采樣點數量帶來的計算量，并結合球形單邊采樣策略特性和高斯攝動方程對采樣點進行修正，再估計傳播后的軌道不確定性，以彌補采用解析模型傳播樣本點導致的精度降低。最后，將提出的算法與高斯和模型相結合，進一步改善軌道不確定性估計精度。

1 基于半解析法的軌道要素快速計算方法

不確定性傳播算法的有效性可以通過使用非線性程度較低的坐標系得到顯著提高。例如，相較于笛卡爾坐標系中的衛星軌道動力學，采用軌道要素作為動力學模型能夠吸收非線性動力學中最主要的項（即引力中的r-2項），使得軌道要素空間的高斯分布能夠更準確地捕捉到在笛卡爾空間中經常觀察到的非高斯行為，并能夠更長時間地保持UR［22］。本文采用經典軌道要素進行軌道不確定性傳播，針對低軌衛星給出了考慮J2 攝動與大氣阻力攝動的軌道要素模型和解析解。

1.1 軌道要素長期項與周期項建模

瞬時軌道要素通常可分為長期項、長周期項和短周期項。而上述長期項和周期項可以基于高斯攝動方程［23］（Gauss variational equations，GVE）進行推導。本文采用NTW坐標系下的描述形式。NTW坐標系以航天器為中心，T軸與軌道相切，以速度矢量所指方向為正方向；W軸沿角動量矢量方向；N軸垂直于T軸和W軸，方向由右手定則確定。當0 ＜e＜1，i≠0，i≠180°時，對應GVE為：

令參數向量α?[a，e，i，Ω，ω，M]T，則在考慮J2攝動和指數模型大氣阻力的影響下，長期項的時間導數［24］為：

式中：ρ0為軌道半徑r0處的大氣密度；K2=(CDS2/m)，K1=(CDS1/m)Q；H為標高；Q=(1 -rPωe；S1和S2分別是垂直于T軸和N軸方向 的橫截面積；rP和vP分別代表近地點半徑和近地點速度；ωe=7.292 115 855 3 × 10-5rad·s-1為地球角速度，RE為地球半徑。

類比文獻［26］中的推導方式，將文獻［24］中給出的大氣阻力長周期項遞推方程進一步推導，可得大氣阻力攝動長周期項解析解αdl（α）為：

式中：ni和nω分別為軌道傾角和近心點角的平均變化率，近似為：

J2 攝動影響下的一階長周期項αl（α）、短周期項αs（α）和大氣阻力攝動影響下的短周期項αds（α）在參考文獻［24-25］中已給出，在此不再贅述。

1.2 任意時刻軌道要素快速計算方法

假設初始時刻為t0，需要獲取t時刻的瞬時軌道要素。一般情況下，可通過數值方法，如龍格庫塔法對式（1）直接進行積分獲取。該方式需要從t0時刻逐步積分到t時刻。然而，在實際情況下，通常只對未來某一時刻或時段內的軌道要素感興趣。例如，在進行碰撞概率計算時，在整個軌道周期內計算碰撞概率顯然是不必要的，通常需要首先進行碰撞時間區間估計，隨后僅在該時間區間內進行碰撞分析［27］。

基于軌道要素長期項和周期項模型能夠快速計算任意時刻軌道要素。在1.1節中將瞬時軌道要素分解為長期項，長周期項和短周期項。由于長期項是線性項，t時刻的軌道要素長期項，即t時刻平均軌道要素約為：

其中，上標表示對應時刻，αˉt0可通過下式獲得：

對于軌道要素周期項的解析解，需要采用瞬時軌道要素作為自變量，而式（8）給出的是t時刻平均軌道要素。因此為了提高精度，t時刻瞬時軌道要素可通過迭代法求解，其步驟為：

1）依據t時刻平均軌道要素計算瞬時軌道要素初值：

2 軌道不確定性半解析快速估計方法

在第1節中給出了快速計算任意時刻軌道要素的方法。因此，在給定t0時刻瞬時軌道要素的均值和協方差后（假設為高斯噪聲），即可選取特定的西格瑪點，通過改進UT 變換進行軌道不確定性傳播。方便起見，將上述算法稱為改進半解析無跡變換（Improved semianalytical unscented transformation，ISUT）軌道不確定性估計方法；ISUT 算法與GMM 結合能夠進一步提高精度，將該算法稱為GMMISUT算法。

2.1 球形單邊采樣策略

目前采用UT 法進行軌道不確定性傳播的文獻通常采用傳統對稱采樣策略，即對于一個ns維空間，需要選擇2ns+1 個西格瑪點。考慮到UT 的計算成本與使用的西格瑪點數成正比，對于高維問題，最小化西格瑪點的數量可以最小化計算成本。文獻［18，28］中給出了球形單邊采樣策略，它僅需ns+2個西格瑪點即可捕獲與傳統對稱采樣策略相當的分布信息，達到與截斷二階濾波器相同的預測能力。因此，本文采用球形單邊采樣策略進行西格瑪點的選取。球形單邊采樣方法通過迭代的方式獲得采樣點，其步驟可總結如下：

1）選擇位于原點（ι=0）和以原點為中心的超球體（ι≠0）上的采樣點權重：

2）使用比例無跡變換調整權重：

式中：比例因子σ∈（0，1］。

3）定義各個采樣點權重：

式中：β是影響第0采樣點協方差權重的參數。

4）當維數大于1 維時，通過式（14）迭代獲得采樣點：

其中，各個向量序列初值為：

2.2 ISUT方法

根據2.1小節中的球形單邊采樣策略獲得采樣點后，選擇初始西格瑪點集：

采用1.2節中的任意時刻軌道要素快速計算方法傳播初始西格瑪點集，可獲得t時刻的西格瑪點集xι（t）。由于該方法計算西格瑪點集所采用的動力學基于GVE 的解析解，存在一定的截斷誤差。為了使得計算結果更接近于GVE 的結果，需要對xι（t）的分布進行調整，即對采樣點進行修正。

由式（14）和式（16）可知，位于超球體原點的第0 西格瑪點x0(t0)=為不確定性分布的均值。而其余ns+1 個西格瑪點位于以原點為中心的超球體上。因此，可通過軌道遞推獲得GVE 動力學對應的t時刻的第0 西格瑪點，計算其與x0（t）的差值Δx，并依據軌道要素間的關系對解析方式獲得的西格瑪點集xι（t）進行修正，從而減小誤差。

本文所采用的動力學模型中平近點角M為快變量，其余5 個軌道要素為慢變量。在進行不確定性傳播時，M發散速度較快，其余5 變量發散速度較慢。因此，對于各西格瑪點的前5個軌道要素，采用依據差值Δx進行平移的修正策略，即：

對于發散較快的M，設計如下修正策略進行補償：

基于修正后的西格瑪點集，t時刻的瞬時軌道要素均值和誤差協方差矩陣為：

則ISUT 軌道不確定性估計算法的流程如圖2所示。

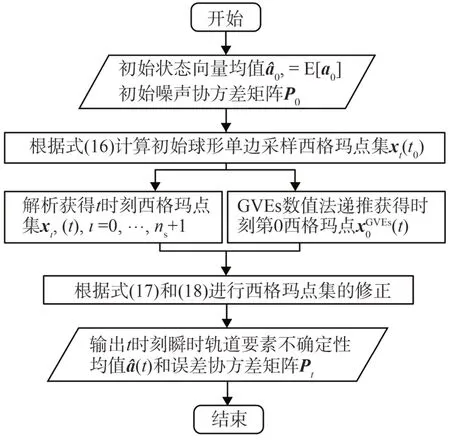
圖2 ISUT軌道不確定性估計算法框圖Fig.2 Diagram of ISUT uncertainty propagation algorithm

最終輸出的t時刻瞬時軌道要素均值和誤差協方差矩陣將用于構建t時刻軌道不確定性的概率密度函數（Probability density function，PDF），即：

式中：N（x；μU，PU）表示正態分布；x，μU=和PU=Pt分別表示輸入變量、均值和誤差協方差矩陣。

2.3 GMMISUT方法

根據式（20）可知，ISUT 法傳播的不確定性PDF是高斯形式的，即僅能夠傳播前2階統計矩（均值與方差）。對于非線性系統，在進行不確定性傳播時，不確定性通常會呈現出非線性特性，即包含了高階統計矩，如峰度和偏度。因此，為了能夠進一步提高半解析法的估計精度，可在初始時刻將高斯形式的不確定性近似為GMM。GMM 是對高斯PDF 的直接拓展，其形式為多個高斯PDF的加權總和：

式中：p（x）為待分解的PDF為p（x）的GMM 近似；ηG，μG，PG分別表示第G分量的權重、均值和協方差。NGM表示GMM 組件的數量。為了確保PDF 的非負性，并確保PDF 曲線下的總面積為1，權重必須是非負的，且總和為1，即：

采用GMM 方法對PDF 進行描述在保留高斯PDF 特性的同時擴展了高斯PDF 的適用性。GMM可以近似多種多樣的PDF，文獻［29］中證明了采用GMM 對PDF 進行近似時，當GMM 組件數量趨向無窮大時均勻收斂。這是一個非常直觀的結果，因為隨著組件協方差趨近于零，GMM 的每個組件都趨向于脈沖函數。因此，通過減小組件的協方差、增加組件的數量，并適當分布組件的均值，可以輕松地近似大部分PDF，且在進行不確定傳播時能夠同時傳播低階和高階統計矩，進一步提升不確定性估計精度。

目前，拆分高斯PDF 有2 種方法，第1 種為在多個方向進行拆分，第2 種為使用單變量拆分庫在一個特定的方向進行拆分［30］。采用第1種方法通常需要求解L2 最小化優化問題，會引入額外的計算量。因此，本文采用第2種方法，將多變量高斯PDF在其最大特征值方向進行拆分，步驟如下：

1）將標準正態分布p（x；0，1）拆分為NGM個均質高斯分布組件：

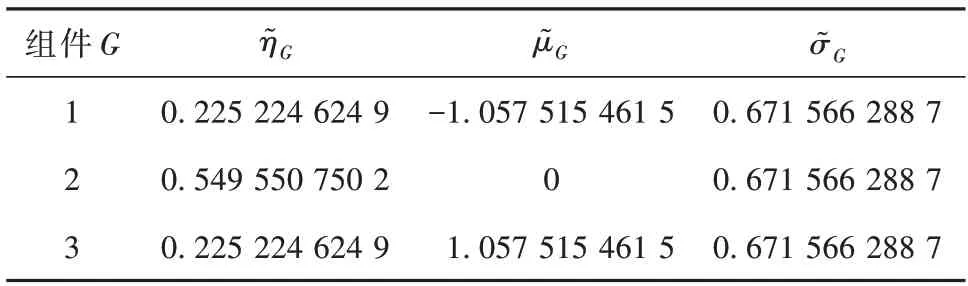
表1 3組件拆分庫Table 1 Three-component splitting library

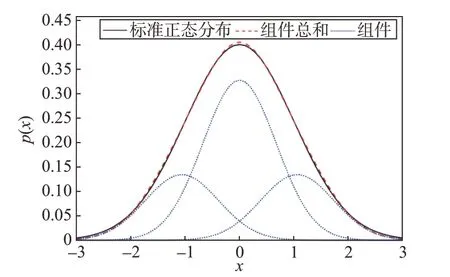
圖3 3組件拆分庫組件及其總和與標準高斯分布的比較Fig.3 Components of the 3-component splitting libraries and their sum as compared with the standard Gaussian distribution

2）采用譜分解將協方差矩陣PU分解為：

式中：Λ是PU的特征值矩陣，λk是第k大的特征值。選擇沿第k個特征向量的方向分解p（x；μU，PU），則式（21）中的參數計算方法為：

式中：υk是PU的第k個特征向量。對于每個GMM 組件，均采用ISUT算法進行傳播，即構成GMMISUT 方法。在應用GMMISUT 實現不確定性傳播的過程中，應合理選擇NGM從而平衡計算效率與精度。

3 數值仿真

3.1 軌道不確定性真實度的似然一致性度量

似然一致性度量L 描述了2 個PDF 之間的重疊程度，對于彼此更一致的PDF來說，L會更大。在將數據點樣本與PDF進行比較的情況下，2個PDF之間的似然一致性度量［32］（Likelihood agreement measure，LAM）定義為：

由于需要分析軌道不確定性PDF 與蒙特卡洛法生成的樣本的一致性，可假設q(x)由狄拉克模型（Dirac mixture model，DMM）給出：

式中：δ(x-μj)是以μj為中心的Dirac-δ分布，權重γj=K-1。若p（x）為高斯PDF，將式（20）和式（27）代入式（26），可得：

若p（x）為GMM的PDF，將式（21）和式（27）代入式（26），可得：

因此，通過DMM 給定1 組樣本點，并與高斯/高斯和模型進行比較，DMM 與高斯/高斯和模型具有相同分布的可能性可以分別通過式（28）和式（29）計算。LAM的值越高，則給定的高斯/高斯和模型更有可能生成DMM。該方法允許將多個高斯/高斯和模型與1 組DMM 進行比較。其中最準確的高斯/高斯和模型具有最高的LAM值。

3.2 初始條件和參數設置

衛星的傳感器通常能夠提供衛星的瞬時位置、速度和時間信息，且無需處理原始偽距或載波信息。為了更貼近真實情況，在地心慣性坐標系中給出衛星初始測量誤差協方差及衛星位置速度均值。假設地心慣性坐標系中衛星的三軸位置和速度誤差標準差分別為100 m 和1 m/s。位置均值rECI=［2 505.35 -6 439.95 1 857.00］ km，速度均值vECI=［2.81 -0.96 -6.84］ km/s。選取樣本點數目為MC=10 000，通過坐標轉換［22］，可得初始瞬時軌道要素的均值和誤差協方差如表2所示。

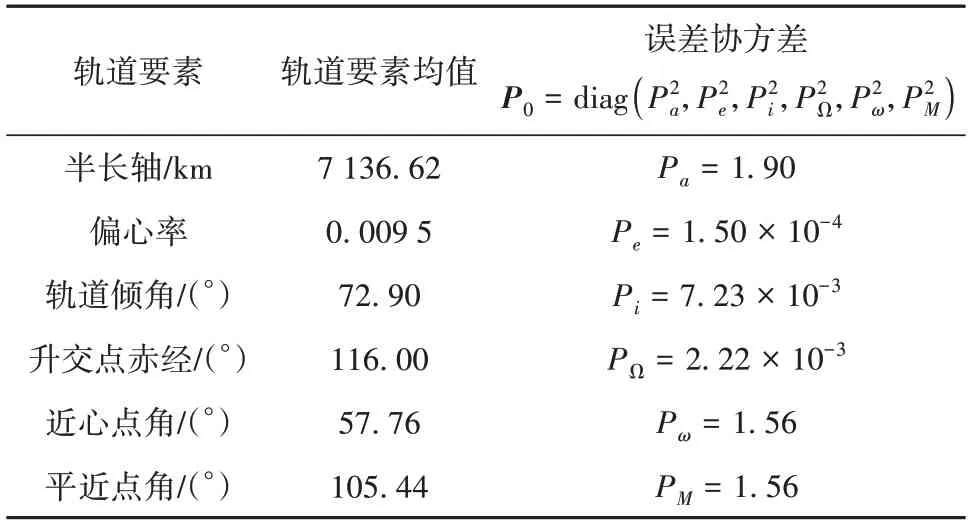
表2 瞬時軌道要素的初始均值與協方差Table 2 Initial mean and covariance of osculating orbital elements

假設初始大氣密度ρ0=2.34 × 10-13kg/m3，密度標高H=68.7 km，阻力系數CD=2.2。航天器垂直于切線方向截面積S1=0.2 m2，垂直于次法線方向的截面積S2=0.2 m2，航天器質量m=10 kg。其他參數：σ=1，β=2，W0=0.25。

3.3 仿真結果與分析

為了比較UT、ISUT和GMMISUT法的計算效率，定義UT 法和ISUT 法的計算消耗時間之比εT（t）、UT法和GMMISUT法的計算消耗時間之比εTG（t）為：

式中：τUT（t）為采用UT算法獲取t時刻軌道不確定性所需的時間，τISUT（t）為采用ISUT 法獲取t時刻軌道不確定性所需的時間，τGMMISUT（t）為采用GMMISUT法獲取t時刻軌道不確定性所需的時間。顯然，當εT(t) ＞1時，ISUT 法的計算效率高于UT法，當εTG(t) ＞1時，GMMISUT法的計算效率高于UT法。

采用ODE45 方法執行UT 法的積分步驟，并與ISUT 法和GMMISUT 法進行比較，結果如圖4 所示。從圖4 中可以看出，當t＜1d時，所需獲取的軌道不確定性所在時刻t越大，ISUT 算法和GMMISUT 算法的計算效率相較于UT算法越高。當t≥1d后，εT（t）和εTG（t）趨于穩定，ISUT 法的計算效率約為UT 法的7.9倍，GMMISUT法的計算效率約為UT法的2.6倍。本文中對比分析所采用的UT 法采用了單邊球形采樣策略，采樣點數目為8個，均需進行積分；對于ISUT法，采樣點數目為8個，需對其中1 個采樣點進行積分；對于GMMISUT法，采樣點數目為24個，需對其中3 個采樣點進行積分。因此可知，上述算法的計算負擔大小主要取決于需要進行積分的采樣點數目。采用ISUT法和GMMISUT 法能夠減小需要數值積分計算的點的數目，因此計算效率更高。

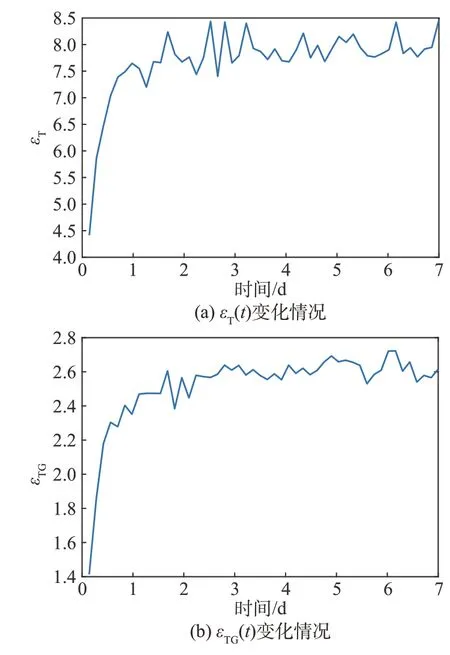
圖4 εT（t）和εTG（t）變化情況Fig.4 The variation of εT（t）and εTG（t）

為了分析采用UT、SUT、ISUT 和GMMISUT 法進行軌道不確定性傳播的精度，根據3.1 小節中給出的LAM 計算方法，分別計算4種算法的LAM 值。在對比分析UT法，SUT 法和ISUT 法時，以ISUT 法的LAM 值為標準進行歸一化，則3 種算法的歸一化LAM 值隨時間變化情況如圖5 所示。可以看出，沒有進行修正的SUT 法的歸一化LAM 值始終較低，對于軌道不確定性跟蹤效果較差。在第1 天內，ISUT法的精度與UT 法相近，甚至整體略優于UT 法。而在第2天之后，ISUT法的精度相較于UT法有顯著的降低。ISUT 算法的誤差大于UT 算法主要是由計算解析解過程中的截斷引起的。相較于SUT法，ISUT法的采樣點修正過程彌補了一部分解析計算造成的精度降低。

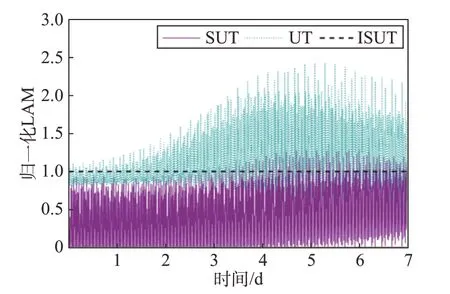
圖5 UT、SUT和ISUT法的歸一化LAM隨時間變化情況Fig.5 Normalized LAM of UT method，SUT method and ISUT method over time

在對比分析UT、ISUT 和GMMISUT 法時，以UT法的LAM 值為標準進行歸一化，則3 種算法的歸一化LAM 值隨時間變化情況如圖6 所示。可以看出，在第1 天內，ISUT 法與GMMISUT 法效果相近，GMMISUT 法的精度略微高于ISUT 法。第2 天之后，GMMISUT 法的精度相較于ISUT 法有顯著提升，且逐漸優于UT 法。這是由于GMM 法的引入使得ISUT 法的精度得以提升。基于GMM 方法的性能與每個組件的協方差有關，協方差越小，結果越好。這一結論具有直觀意義，因為當GMM 中每個分量的協方差趨于零時，每個分量就會變得越來越像脈沖函數。從而更輕松地近似各種PDF。結合圖4 和圖6 可知，GMMISUT 法在計算效率優于UT 法的同時，在大部分時段給出了優于UT法的結果。

圖6 UT、ISUT和GMMISUT法的歸一化LAM變化情況Fig.6 Normalized LAM of UT method，ISUT method and GMMISUT method over time

4 結論

對于軌道不確定性傳播問題，提出基于半解析法和球形單邊采樣無跡變換的軌道不確定性快速估計方法。該方法的特色為采用球形單邊采樣無跡變換結合高斯攝動方程及其解析解進行采樣點的傳播和修正，從而實現軌道不確定性快速估計。其中解析解考慮了J2 攝動和大氣阻力攝動的解析形式，被用于實現樣本點的快速傳播，加快計算效率；球形單邊采樣在保證二階精度的同時進一步降低計算量；基于高斯攝動方程和采樣點特性的采樣點修正緩解了由采用解析解進行樣本點傳播導致的精度降低問題。將該方法與GMM 結合能夠進一步提高精度。仿真分析表明，所提算法在保證合理精度的同時，大幅提升了不確定性估計的效率，適用于在軌不確定性快速傳播，可為在軌避障分析等提供初始輸入。