單噴嘴模型火箭發動機中高頻不穩定燃燒的預測

王治宇，陳朋，林偉，仝毅恒，郭康康，黃衛東，聶萬勝

（航天工程大學宇航科學與技術系，北京 101416）

0 引言

高頻不穩定燃燒問題在液體火箭發動機、固體火箭發動機、燃氣輪機等熱力裝置中廣泛存在［1-2］。其誘發原因是非定常熱釋放與燃燒室內聲波的相互耦合。高頻不穩定燃燒會引發高幅值周期性壓力振蕩和熱負荷急劇增加，對燃燒室造成巨大破壞。不穩定燃燒問題的發生涉及湍流燃燒和傳熱、化學反應、火焰和聲波的相互作用等［3-4］，而這些過程又有著不同的時間尺度。因此，長久以來并沒有普適的數學物理模型將其徹底描述清楚。在液體火箭發動機中，工程上采用隔板、聲腔等被動控制裝置對不穩定燃燒進行抑制。但這通常以犧牲燃燒效率、增加燃燒室重量和結構復雜性為代價，甚至需要進行多次全尺寸試車才能確定被動控制裝置的有效性。主動控制技術則是通過傳感器和控制機構等，對推進劑流量等變量進行控制，避免不穩定燃燒的發生。不穩定燃燒的“早期辨識”和“提前預測”可為未來在液體火箭發動機中發展主動控制提供技術支撐。近年來，基于數據驅動的不穩定燃燒早期辨識與預測越來越具備可行性［5-7］。

分析燃燒過程的混沌動力學特性變化是研究不穩定燃燒早期辨識和預測的可行途徑。高頻不穩定燃燒的發展過程通常表現為從燃燒噪聲到熱聲耦合極限環振蕩的演變［8］，該過程伴隨著非線性混沌動力學特性的變化。文獻［9］表明，燃燒噪聲階段往往體現了較強的混沌特性，而不穩定燃燒的發展階段則經歷了混沌特性的減弱。燃燒噪聲階段的壓力擾動是非周期性的，在經過Hopf 分岔后，將演變為等振幅的極限環震蕩［10］。Murayama等［11］和Gotoda等［12］指出，燃燒噪聲階段的混沌動力學特性能預測燃燒系統后續的重要變化。為此，Kasthuri等［13］基于普渡大學的矩形發動機試驗數據，利用遞歸定量分析和多重分形理論等，研究了多種非線性特征在熱聲耦合早期辨識中的可行性。Lyu等［14］采用統計學指標和人工神經網絡對環形燃燒器的熱聲耦合預測問題進行了研究。然而，上述研究主要采用單次試驗數據進行驗證，較難考察這些方法的泛化能力。采用的指標較為單一，這在一定程度上限制了模型非線性特征的表達能力和通用性。單一的指標難以刻畫燃燒室內動力學特征的非線性，導致無法細致區分不同燃燒狀態。這些指標往往與燃燒室幾何構型、推進劑組合等因素密切相關，開展早期辨識或預測時采用的閾值也隨之變化，嚴重限制了模型的通用性。比如，當改變燃燒室幾何構型后，原先適用的閾值和指標可能不再適用。

高頻不穩定燃燒預測的兩個挑戰是早期辨識的有效性和預測模型的魯棒性。早期辨識的有效性是指不穩定燃燒尚處于發展階段時的預測。液體火箭發動機可在極短的時間內（100 ms）［1］從穩定運行狀態發展出高頻不穩定燃燒。在如此短的時間內捕捉熱聲振蕩的相關特征并進行預測是極大的挑戰。預測模型的魯棒性指深度學習模型的泛化能力。比如，燃燒室幾何構型調整后預測模型的可應用性。

為應對這兩個挑戰，引入機器學習模型建立預測模型。這既能增強模型對燃燒信號中非線性特征的刻畫能力，又便于建立更為通用的不穩定燃燒預測框架。Sarkar等［15］針對高速攝影的圖片序列，基于深度學習開展了燃燒不穩定性的實時診斷。Kobayashi等［16］研究了利用壓力信號和釋熱速率等信息來開展燃燒不穩定性預測的可行性。Cellier等［5］基于旋流燃燒器的試驗數據，開展了基于深度學習的燃燒不穩定性預測，取得了較好的效果。Lyu等［6］利用長短時神經網絡對環形燃燒室的聲壓進行了預測，實現了不穩定燃燒的早期辨識，證明了該方法提前預測熱聲耦合的有效性。

上述研究表明，燃燒室的動態壓力信號、釋熱信號等，能揭示燃燒噪聲的非線性動力學特征，具備開展燃燒不穩定性預測的潛力。注意到，相比于原始信號，遞歸矩陣［13］中包含了豐富的混沌動力學特征，且便于與深度學習模型相結合進行特征的提取與計算。因此，本文提出采用遞歸矩陣作為深度學習模型的前處理步驟，利用深度學習模型對這些矩陣特征進行訓練，基于大量的熱試車試驗數據開展有監督學習，從而對高頻不穩定燃燒進行提前預測。為驗證早期辨識的有效性和預測框架的魯棒性，采用包含不同運行工況和燃燒室幾何構型的熱試車試驗數據進行訓練和預測［17］，既能考察早期辨識的有效性，又能對預測模型的泛化能力進行驗證。

1 試驗裝置和試驗數據

單噴嘴火箭模型發動機采用的推進劑為氧氣/甲烷，實物圖如圖1 所示［17］。發動機結構的細節尺寸如圖2 所示，其中氧噴嘴總長度70 mm，靠近氧腔的上游部分內徑為9.6 mm，靠近燃燒室的下游部分內徑為8 mm，甲烷環縫寬度為1 mm，噴嘴縮進長度為2 mm。該發動機采用同軸剪切式噴嘴，氧氣經由氧腔沿軸向通過氧噴嘴進入燃燒室，甲烷通過8 個徑向孔進入噴嘴環縫，氧氣和甲烷在噴嘴縮進室發生最初的相互作用，之后進入燃燒室。燃燒室為圓柱形燃燒室，直徑35 mm，可變長度在180 mm到452 mm 之間。噴管內型面為帶有收縮和擴張段的拉瓦爾噴管，噴管喉部直徑21 mm，擴張比為2.7。發動機采用火花塞點火方案，火花塞安裝在燃燒室側壁，距離噴注面60 mm，單次點火能量2 J，點火頻率50 Hz。發動機熱試車試驗過程中的動態壓力測量主要通過安裝在燃燒室側壁面的壓電式動態壓力傳感器實現。該傳感器型號為Kistler 6043A，量程為±10 MPa，數據采樣頻率為100 kHz。兩支動態壓力傳感器的安裝位置分別為距離噴注面37 mm處和距離燃燒室尾部端面37 mm 處。熱試車試驗中，獲得的高頻燃燒不穩定性類型包括一階和二階縱向不穩定。采用高頻壓力傳感器能完整捕捉到燃燒室內動力學系統的變化。因此，高頻動態壓力信號可作為預測框架的輸入信號。

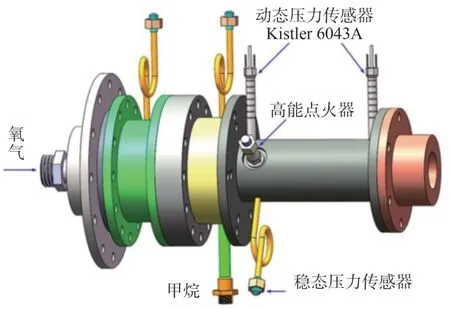
圖1 氣氧甲烷單噴嘴火箭模型發動機［17］Fig.1 O2/CH4 single-injector model rocket combustor［17］

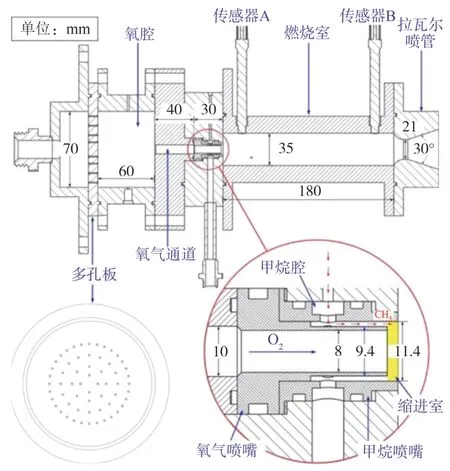
圖2 發動機結構示意圖［17］Fig.2 Structure schematic of the rocket combustor［17］

圖3 為高頻不穩定燃燒的試驗數據結果，其中圖3（a）為靠近燃燒室頭部的高頻壓力傳感器記錄的壓力-時間軌跡，在等幅振蕩階段，壓力振蕩峰-峰值約為0.25 MPa，占比平均室壓25%。圖3（b）為圖3（a）中壓力信號的時頻譜圖。時頻譜圖中，短時傅里葉變換的每個計算窗口大小為4 096 個數據樣本，重疊數據樣本為2 048個。由于采用的是火花塞點火，圖中所出現的壓力峰為點火壓力峰。大約經過50 ms后，燃燒室發展為典型的熱聲不穩定燃燒。

圖3 前三組熱試車試驗的動態壓力及對應時頻譜圖Fig.3 Dynamic pressure signals and corresponding spectrogram of the first three groups of hot tests

標準運行工況條件下，氧氣和甲烷處于室溫（約為295 K），流量分別為0.17 kg/s 和0.08 kg/s。通過熱力計算程序CEA（Chemical equilibrium with applications）計算可得燃燒室壓力為1.225 MPa，燃燒室溫度為2 692 K。氧氣和甲烷流量通過推進劑供應管路中的音速噴嘴控制。試驗時控制系統根據設定時序，控制電磁閥和火花塞的開關來控制發動機點火和熄火，并采用富氧點火和富燃關機方案，燃燒室采用熱沉冷卻，因此每次試驗點火時間較短。25 組試驗中均發生了明顯的熱聲耦合不穩定。如表1所示，不同熱試車試驗之間，幾何構型和運行工況略有變化，因此高頻不穩定燃燒的主頻和振型也會相應發生變化。試驗過程中一共出現了兩種高頻燃燒不穩定性，分別對應一階縱向和二階縱向模態。二階縱向模態都出現在燃燒室長度為316.5 mm的試驗中，其余均為一階縱向模態。

表1 各組試驗操作設置情況Table 1 Overview of used test runs

2 預測模型

2.1 預測框架構建

模型的訓練和預測都基于滑動窗口的形式，如圖4 所示。若當前時間窗動態壓力的振蕩峰-峰值低于平均室壓的10%，則認為該時間窗樣本是穩定燃燒樣本，否則為不穩定燃燒樣本。樣本的標簽為：若下個滑動時間窗樣本為不穩定燃燒，則當前時間窗標記為陽性（positive），否則為陰性（negative）。據此對剩下25 組試驗數據進行滑動窗口劃分和標簽的標定。采用交叉驗證的方式來評估模型泛化能力。以第一組試驗數據作為測試組為例，使用剩下的24 組試驗數據進行訓練。輸入信號為各個組動態壓力時序的時間窗樣本，輸出為陰性或陽性的二進制標簽，即二分類的輸出。為評估模型的準確率，采用若干評價指標，包括準確率、受試者工作特性（Receiver operating characteristic，ROC）曲線等［7］。

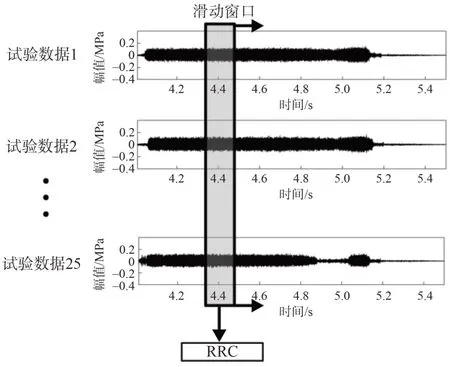
圖4 通過時間切片的滑動窗口對不同試驗樣本進行操作Fig.4 Manipulating different experimental samples through sliding windows of time slicing

總體框架如圖5 所示，包括兩大部分。第一部分是基于混沌動力學分析的前處理，通過混沌分析將壓力時序轉化為遞歸矩陣（Recurrence matrix），從而提取壓力信號的非線性特征。第二部分是基于深度學習的預測計算模塊［18］。骨架網絡為ResNet-18模型和CBAM（Convolutional block attention module）注意力模塊［19］。其中，Resnet-18 模型的主干網絡由18層網絡組成，包括多種卷積層（Convolution）、池化層（Maxpooling）、歸一化層等。ResNet-18 模型是深度學習領域代表性的模型，可用于提取遞歸矩陣的特征。CBAM 注意力模塊為嵌入式模塊，用于提升網絡模型的準確率。預測框架的輸入信號為傳感器記錄的高頻動態壓力。輸出變量為：0 表示穩定燃燒（陰性），而1 表示不穩定燃燒（陽性）。為便于分析，將該框架記為RRC。

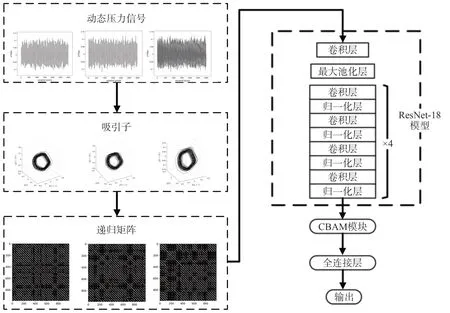
圖5 RRC模型的燃燒不穩定預測總體框架Fig.5 The technical framework of the RRC model for combustion instability prediction

2.2 遞歸矩陣

相空間重構計算遞歸矩陣的第一步，通過將壓力振蕩信號組成的時間序列拓展到高維空間，在一定程度上恢復吸引子結構，從而獲得系統的非線性特征。根據Takens 定理［20］，對于N個離散數據對應的一維壓力時間序列{p'(i)|i=1，2，…，N}，引入延遲時間τ和適當的嵌入維度m可構建相空間矢量：

式中：t=1，2，…，N-(m-1)τ。

根據Takens 的理論，時間延遲和嵌入維數是互不相關的，因此可以對其獨立求解。本文采用自相關函數法對時間延遲進行計算［21］，采用Cao 方法計算嵌入維數［22］。確定了最佳時間延遲和嵌入維數后，可計算相應的遞歸矩陣［20］。

首先進行相空間重構，得到維度為m，時間延遲為τ的時間序列。按照式（2）計算重構時間序列中第i向量、第j向量的距離：

進一步根據式（3）計算遞歸矩陣：

式中：ε是閾值常數，H1為Heaviside函數。

3 結果與討論

3.1 模型訓練過程

基于滑動窗口劃分，得到所有試驗數據集對應的遞歸矩陣即可完成深度學習模型的前處理。隨機抽取80%的數據集作為訓練集，開展深度學習模型訓練。其余為驗證集，以監測訓練過程。訓練環境為搭載Nvidia 3080 顯卡的Cuda 11.2，并在該環境下基于Pytorch搭建深度學習框架。

3.2 模型預測結果與討論

標簽集由0 和1 組成，分別表示陰性（穩定燃燒）和陽性（不穩定燃燒）。將測試集輸入到訓練好的模型后，輸出的是0 到1 之間的概率，即表示在下一個時間窗口內發生不穩定燃燒的概率。輸出與標簽集之間的誤差則用于評估模型預測的準確性。當模型輸出超過0.5，表明下個時間窗內會發生燃燒不穩定，反之則不發生燃燒不穩定。準確率指標a定義為：

式中：NS表示需要測試的數據總量；ni表示其中第i條數據的準確率，具體計算方式如下：

式中：H2為Heaviside函數為RRC的決策值，y為真實的標簽值。

以第一組熱試車數據為例時，在交叉驗證過程中，使用剩下的24組數據對預測模型進行訓練。以訓練后的模型對第一組試驗數據進行測試，與真實標簽值對比后得到準確率。進行驗證測試的試驗數據對預測模型而言是未知的，可以較好地驗證模型的泛化能力。特別是，25 組試驗中包含了不同燃燒室幾何構型和運行工況的數據，這更加考驗模型的泛化能力。完成交叉驗證后，得到25組測試的準確率，如圖6所示。可以看到，所有測試評估組的準確率都穩定在95%以上，且其中大部分組的準確率超過了98%。因此，交叉驗證的準確率結果較好地驗證了預測模型的有效性和泛化能力。

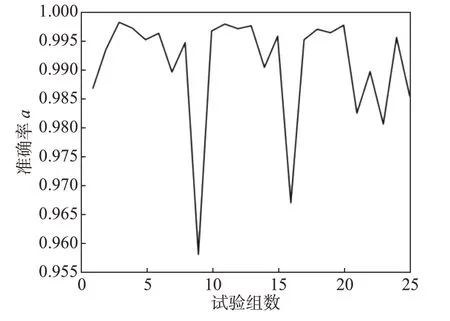
圖6 交叉測試組的準確率結果Fig.6 Accuracy results of the cross testing group

注意到試驗數據集陰性和陽性的樣本分布是不平衡的。在不穩定燃燒的預測中，最重要的是盡可能辨識到那些可能發生燃燒不穩定的樣本，從而采取相關控制措施提前避免。因此，為進一步刻畫預測模型在不同標簽數據下的表現，引入混淆矩陣對陰性和陽性樣本進行量化分析。該矩陣可描述預測類別和實際類別之間的差異。對于二分類的模型，結果可分為以下4 種。真陽性樣本（True positive，sTP）：模型預測為發生不穩定燃燒的樣本，實際也為不穩定燃燒；假陽性樣本（False positive，sFP）：模型預測為發生不穩定燃燒，但實際情況是穩定燃燒的；真陰性樣本（True negative，sTN）：模型預測為穩定燃燒，實際情況也是如此；假陰性樣本（False negative，sFN）：模型預測為穩定燃燒，但實際情況中卻發生了不穩定燃燒。

當模型預測樣本為陽性，即發生不穩定燃燒時，只有相對較少的一部分屬于誤判。這意味著預測模型應用在實際發動機中時，做出陽性決策的可信度比較高。可以用精確率φ來表示預測結果為陽性的樣本中正確預測的比例：φ=sTP(sTP+sFP)。

精確率越高，模型的陽性預測的可信度也越高。前4 組數據測試后的精確率分別為：92.00%，100%，92.51%，99.65%，這表明了預測模型辨識不穩定燃燒的可信度是非常高的。另一個指標是假陽性率φfpr，可以形象地理解為誤診率，即錯誤地將原本屬于穩定燃燒的樣本誤判為發生不穩定燃燒，計算方式為：φfpr=sFP(sFP+sTN)。

前4 組數據試驗測試后的假陽性率分別為14%，0.00%，16%，0.78%。可見第二組和第四組的假陽性率非常低，而第一組和第三組相對更高。這意味著在第一組和第三組中，有一部分穩定的樣本被模型誤判為會發生不穩定燃燒。從不穩定燃燒的實際意義來分析，更為關鍵的是不能丟失對不穩定燃燒樣本的預測，所以假陽性率偏高依然是可以接受的。此外，引入召回率η來表征模型對所有陽性樣本的識別成功率。計算方式為：η=sTP(sTP+sFN)。

召回率的現實意義在于預測模型有多大的概率預測出全部的不穩定燃燒樣本。當沒有成功預測出后續發生的不穩定燃燒時，發動機將面臨不穩定燃燒的危害。因此預測模型應追求更高的召回率，從而避免在預測中出現不穩定燃燒樣本的丟失。經計算，前4 組試驗數據測試后的召回率分別為100.00%，96.66%，100.00%，96.56%。由此可見，預測模型對不穩定燃燒（陽性樣本）的預測成功率非常高，其中只有很少一部分陽性樣本被誤判為了穩定燃燒樣本。在不穩定燃燒的預測中，為捕捉到更多的不穩定燃燒樣本，即追求更高的召回率，可以犧牲一定的假陽性率為代價，這可以通過降低一定的預測閾值來實現。此時模型將更加傾向于將樣本預測為不穩定燃燒，從而采取主動控制措施以避免不穩定燃燒。在實際發動機中，假陽性率偏高的代價是模型會錯誤地將穩定樣本也預測為不穩定燃燒。召回率偏低則表明許多實際發生了不穩定燃燒的樣本并沒有被成功預測，導致系統并未對不穩定燃燒采取措施。因此相對而言，召回率偏低的代價會造成更顯著的危害。由此可見，以假陽性率為代價換更高的召回率，通常是可行的。

召回率又被稱之為真陽性率φtpr，與假陽性率φfpr組合后可進行ROC曲線的計算［5］，能很好地刻畫非平衡樣本中模型的分類性能。假陽性率為ROC曲線的x軸，真陽性率為y軸。通過調整模型的閾值可獲得不同的φtpr/φfpr數據坐標點，也就是模型對應的ROC曲線［5］。

ROC 曲線可以動態評估預測模型將以多大的誤判代價來實現不穩定燃燒樣本的成功預測。當假陽性率很低時，性能優秀的模型仍能保持較高的真陽性率。因此性能越好的模型，對應的ROC 曲線應更逼近ROC圖中的左上方。以前4組試驗數據為例，計算ROC曲線，如圖7所示。

李庚先生自幼喜愛中國古典文學藝術，對繪畫更加癡迷，秉承其父李可染訓教，鉆研水墨，取得了豐碩成果，在國際上聲譽日隆。清華大學教授、李可染畫院副院長王魯湘贊其“血液中流淌著父親李可染先生對神秘崇高的宇宙精神悠然神往的可貴品質。他對自然神性有一種發自靈府的會意……山水風云的無言大美，水墨語言的玄化鴻蒙，在他看來都是道通天地的律動，他所做的就是‘從而和之’，讓氣韻發自筆端。李庚的水墨畫把父親早年的墨戲和晚年的抽象推到了一個風神飄舉的境界，其繪畫作品玄韻淡泊，情思淹濟，風氣韻度似父親而更恣縱邁達”。

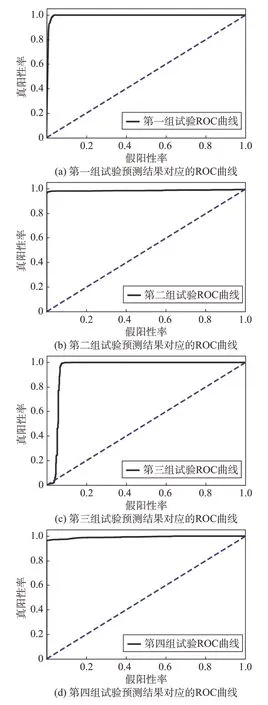
圖7 前4組熱試車試驗數據預測結果的ROC曲線Fig.7 ROC curves of the first four hot-fire tests

進一步分析圖7，注意到所有的ROC 曲線都經過坐標點（0，0）和坐標點（1，1）。當閾值設定為最高時，所有預測結果都為陰性，偽陽性率φfpr和真陽性率φfpr都為0，此時對應坐標點（0，0）。當閾值設定為最低時，所有預測結果都為陽性，此時偽陽性率和真陽性率都為1，對應了ROC 曲線的坐標點（1，1）。圖中的虛線表示隨機模型的ROC曲線。

圖7中，4 組試驗數據的ROC 曲線體現了非常理想的預測結果。為進一步考察預測模型在不穩定燃燒發展過程中早期辨識的能力，以這4 組試驗數據為例，將不穩定燃燒發展過程中模型的決策函數和實時壓力數據進行對比，如圖8所示。

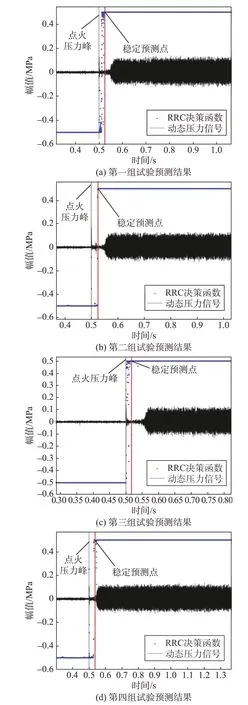
圖8 前4組的壓力信號與對應的RRC模型預測結果對比Fig.8 Dynamic pressure signals of the first four verified groups and corresponding prediction results obtained by RRC model

熱試車試驗中，高頻不穩定燃燒發展速度極快，只需要100 ms 左右的時間。對早期辨識的準確性和有效性提出了較高的要求。圖8中的預測點表示RRC 模型的實時預測值，而黑色實線為實時動態壓力信號。為方便與壓力信號進行對比，將輸出值閾值從0.5 調整為0。低于閾值的輸出表示下一個時間窗口內不會出現不穩定燃燒，反之則表示會發生不穩定燃燒。

在0.5 s出現的點火壓力峰之前，模型的預測穩定維持在閾值下方。發動機未點火啟動之前，傳感器所測的系統噪聲與后續是否發生不穩定燃燒是無關的。但預測模型也需要能夠對這一過程的物理信號進行辨識和預測，以保證預測運行的連續性。燃燒室內點火后形成了極高的壓力峰，壓力的劇烈振蕩改變了燃燒室的動力學特性。預測模型的輸出值也隨之產生變化，在閾值下方產生了逐漸增加的趨勢。但由于此時模型仍然無法判斷系統后續是否會發生不穩定燃燒，一段時間內仍處于閾值以下。隨著時間窗口繼續滑動，預測系統采集到更多的動力學特征，此時的預測值超過了閾值，表明下個時間窗內發生不穩定燃燒的概率超過了0.5。

在閾值附近區域振蕩一段時間后，最終穩定在閾值上方的水平。此時表明了預測系統判斷下一個時間窗內發生不穩定燃燒的概率非常大。而在之后的不穩定燃燒階段，模型輸出值一直穩定保持在閾值上方的水平。這是因為發生了不穩定燃燒后，動力學特征容易區分和預測。由此可見，燃燒狀態監測的實現是簡單且穩定的，較難預測的是由穩定燃燒噪聲階段到熱聲耦合階段發展的過程。

在不穩定發展階段（從點火后到熱聲振蕩階段），當預測的輸出值穩定在最大值附近時，認為模型已完成熱聲耦合動力學特征的早期辨識，實現了不穩定燃燒的提前預測。將這一時間節點稱為穩定預測點，如圖8 所示。穩定預測點到最終試驗中發展出不穩定燃燒的時間，是模型預測該組試驗不穩定燃燒的提前時間。4 組的預測提前時間分別為：31.52 ms、34.58 ms、47.16 ms、20.15 ms。這4 組熱試車的平均提前預測時間為33.35 ms。經計算25組預測結果后，平均提前時間為35.28 ms。

綜上，基于前4 組試驗數據對預測框架進行了有效性和泛化能力的評估，考察了預測準確率、精確率和ROC 等指標，并分析了各組的提前預測時間，可為主動控制系統提供一定時間裕度。

4 結論

本文提出了一種較為通用的高頻不穩定燃燒早期辨識和預測分析框架。該框架融合了遞歸矩陣和深度學習模型。遞歸矩陣作為ResNet-18 深度學習模型的前處理，可提供關于燃燒噪聲的非線性動力學特征。ResNet-18 模型可基于遞歸矩陣進行大量試驗數據的有監督學習，從而對未知的熱試車試驗進行燃燒不穩定性的早期辨識和預測。基于25 組熱試車試驗的交叉驗證，評估了預測框架的有效性和魯棒性。結果表明，本文提出的高頻不穩定燃燒預測框架可實現熱聲耦合的早期辨識和預測，平均提前時間為35.28 ms。