融合演化動力和網絡結構的供應鏈生態系統韌性評估研究

陳洪業

（湖南工業大學商學院， 湖南 株洲 412007）

0 引言

我國“十四五”規劃提出“增強制造業競爭優勢，提升產業鏈供應鏈現代化水平；促進數字技術與實體經濟深度融合，賦能傳統產業轉型升級”。制造業供應鏈生態系統韌性評估和韌性提升對策的提出能為產業行動方案的制定提供重要理論基礎，也能有效支撐制造業供應鏈的長足發展，引起了學界的持續關注與討論。株洲市作為湖南省唯一的全國首批產業鏈供應鏈生態體系建設試點城市，力圖推動優勢產業鏈供應鏈韌性和安全水平提升，為建設制造強國貢獻株洲智慧和力量。然而，目前株洲市制造業供應鏈生態系統建設仍處于起步階段，還存在整體運作效率不高、數智基礎薄弱、敏捷性和柔性有待加強等問題，難以應對突發風險。因此，如何提升株洲市制造業供應鏈的韌性成為了亟待解決的問題。本研究以株洲市為例，綜合運用復雜網絡理論、生態系統理論等，構建韌性評估模型，并根據評估結果提出韌性提升對策，為供應鏈生態系統韌性評估與提升研究提供理論依據。

1 研究方法及數據來源

1.1 社會網絡分析

社會網絡分析（SNA）方法是以節點及連邊構成的互相關聯的網絡作為研究對象[1]，依據節點之間的聯系狀況對其網絡的拓撲結構進行量化分析的一種關鍵分析方法。隨著區域經濟理論等交叉學科的不斷發展，越來越多的學者將社會網絡分析方法運用于供應鏈網絡來進行研究[2]。據此，本研究從節點、連邊及網絡整體三個方面選取多個特征指標（見表1），從網絡拓撲結構的角度對株洲市供應鏈生態系統韌性進行評估。

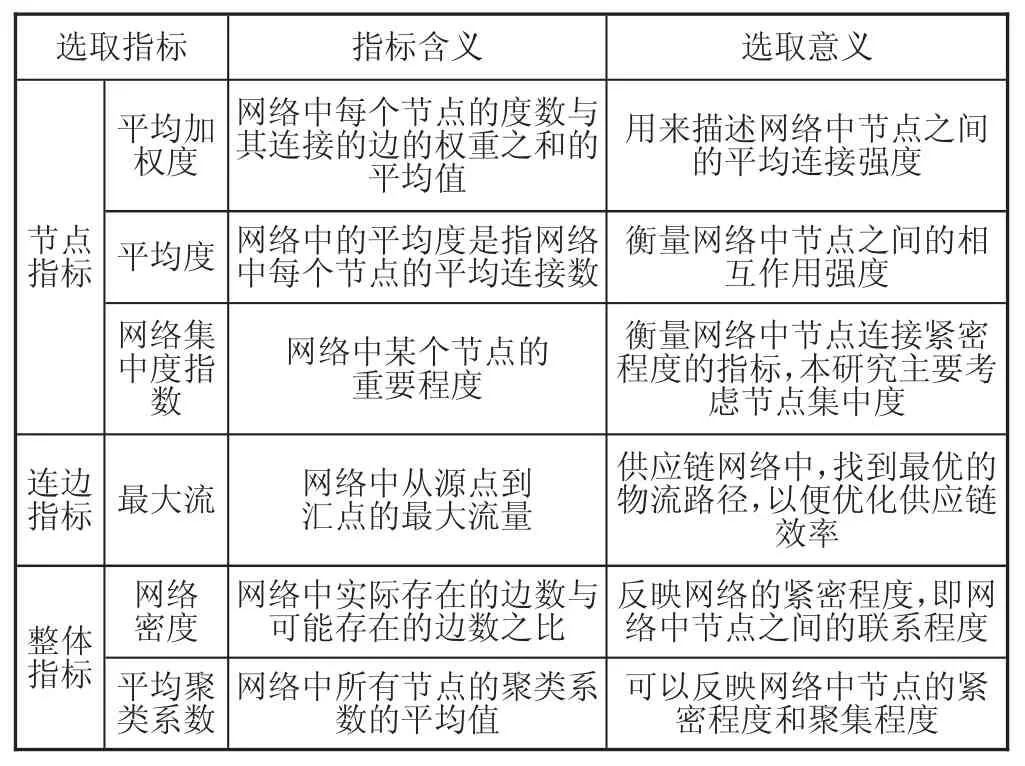
表1 本研究所選取的網絡結構指標

1.2 模糊物元及復合模糊物元

模糊物元方法由于能夠處理不確定和模糊性問題，應用廣泛，在韌性評估的研究上已取得了一定的進展[3-4]。但是，鮮有研究針對供應鏈韌性進行評估研究，尤其是供應鏈生態系統錯綜復雜、相互依賴、關聯互動、共生共存[5]，則需要從生態系統的演化動力及其網絡化結構兩方面著手，而模糊物元能夠靈活地處理輸入變量和輸出變量之間的非線性關系，進而對供應鏈生態系統的韌性進行評估與分析。

1.2.1 模糊物元模型

1）模糊物元及復合模糊物元。在進行物元分析時，待評價的事物M及其所包含的特征指標C與其對應的量化值x組成物元模型（R（R=（M，C，x）或R=（M，C，C，（M））），此時若具有模糊屬性，則可以將其為模糊物元模型。

假設對株洲市M個年份的供應鏈生態系統進行韌性評估，每個年份選取n個指標，每個指標C都有與其對應的值x，那么就可以構建M個年份的n維復合模糊物元矩陣Rmn，即：

式中：Rmn為M個年份的n個模糊指標的復合物元；Mi為第i個年份（i=1，2，…，m）；Cj為第j個指標（j=1，2，…，n）；xij為第i個年份第j個指標對應的模糊量值。

2）從優隸屬度模糊物元。從優隸屬度指的是各指標值從屬于標準值所對應的模糊值的隸屬程度。本研究所構建的供應鏈生態系統韌性評估指標體系中，所選擇的指標均為正向指標，即指標對評估結果均為促進作用，且均為正向值，因此，可稱其為從優隸屬度原則，其計算公式如下：

3）標準模糊物元與差平方復合模糊物元。標準模糊物元R0n指的是從優隸屬度模糊物元中各項評價指標的從優隸屬度的最優最大項，由于在本研究中選取正值，且越大越好，因此選取最大值為最優項，即各指標從優隸屬度μ0j=1。

然后，以Δij（i=1，2，…，n；j=1，2，…，m）表示標準模糊物元R0n與復合從優隸屬度模糊物元中各項差的平方，構建出差平方復合模糊物元矩陣RΔ，即Δij=（μ0j-μij）2，其計算公式為：

1.2.2 熵權法確定權重系數

熵權法來確定指標的權重系數是一種操作簡單的客觀賦權法，熵權的概念由香農引入信息論，由于其可操作性強的優點，已在多個學科及領域得到了廣泛的應用。

熵權系數的確定步驟如下所示：

1）原始矩陣構建。構建M個年份的n個評價指標的原始矩陣R：

式中：xij為第j個年份在第i個指標上的值，xij∈[0，1]。

2）歸一化處理。主要思想是對原始矩陣進行歸一化處理，得到判別矩陣B，方便后續的計算與結果分析；根據供應鏈生態系統韌性評估指標的特征，對于越大越優的指標而言，采取如下最大最小的歸一化方法：

3）熵值定義與計算。根據熵的定義，可以確定熵的計算公式為：

4）供應鏈生態系統韌性評估指標熵權w計算：

1.2.3 貼近度和綜合評價

貼近度指的是待評價值與標準值之間的遠近程度，數值越大表示距離越近，數值越小表示距離越遠[6]。因此貼近度的大小可以用來判斷各年份下供應鏈生態系統韌性的變化情況。

考慮到在供應鏈生態系統韌性評估中各個指標的實際意義，本研究采用歐氏貼近度ρHj來對最終的評估做出計算：

式中：ρHj為各年份下的歐式貼近度。

1.3 數據來源及預處理

本研究的數據分為兩部分，其一是演化動力指標的數據，來源于《株洲市統計年鑒》；其二是網絡結構數據，采集快遞100[7]（https：//www.kuaidi100.com/）的株洲市下屬各區縣物流網點的數據。其中，數據缺失的部分利用插值法補齊。

2 實驗結果與分析

2.1 基于復雜網絡的供應鏈生態系統構建

獲取了株洲市快遞100 的數據后，根據改進的引力模型公式[8]，計算兩兩區域間的網點引力。

式中：Gij為兩個區域節點i和j之間聯系的強度；Zi和Zj分別為區域i和j的網點個數；rij為兩個區域i和j間的距離（在百度地圖上搜索連區域間的距離，以最短距離作為兩個區域間的距離rij）；e為自然對數的底數。

隨后，基于兩兩區域間的網點引力，可以構建2012 年、2016 年及2020 年三年的基于無向復雜網絡的供應鏈生態系統（見圖1）。

圖1 2012 年、2016 年及2020 年株洲市基于復雜網絡的供應鏈生態系統結構

分析可知，這三年來，從網絡整體來分析，網絡的密度越來越大，由0.328 提升到0.660，其中，天元區與石峰區的聯系越來越密切；從網絡連邊視角來分析，平均最大流不斷增大，說明各區域之間的供應聯系越來越強；從網絡節點視角來分析，在不斷的聯系演化下，天元區在網絡中的位置日益凸顯了出來，成為了網絡中最具影響力的節點，其發展速度在全市也是保持的最大增長幅度，到2020 年時，節點的加權度值已經達到了24.107 提升到了32.143。

2.2 供應鏈生態系統韌性評估指標體系構建

在梳理相關文獻的基礎上，根據株洲市供應鏈生態系統的演化發展特點和發展現狀，初步提出供應鏈生態系統韌性評估指標，最終分別從供應鏈生態系統演化動力和系統網絡結構兩個維度，構建出包含三級指標的供應鏈生態系統韌性評估指標體系，包括一級指標2 項、二級指標5 項、三級指標16 項（見表2）。

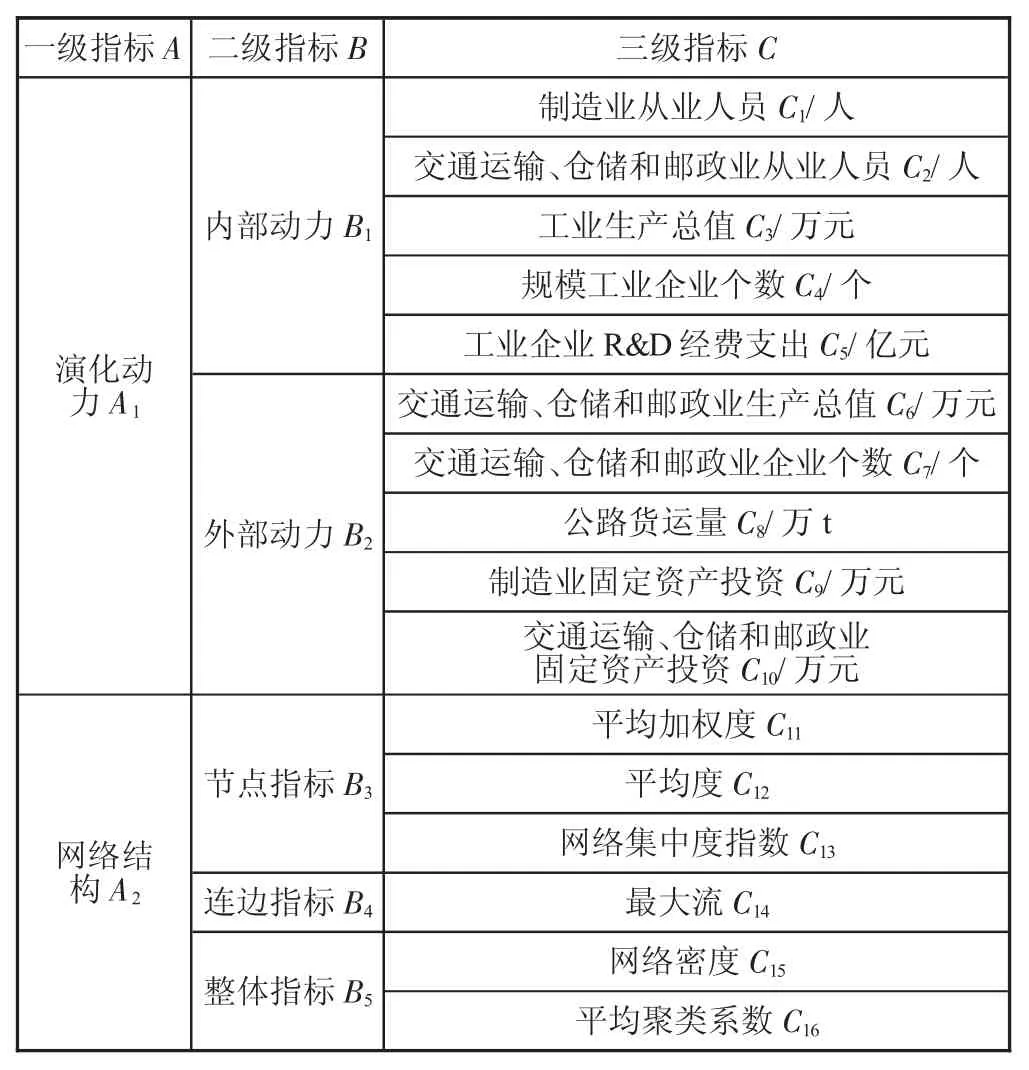
表2 供應鏈生態系統韌性評估指標體系

2.3 評價模型構建及結果計算

根據前述的模糊物元法，構建株洲市供應鏈生態系統韌性評估模型：

1）依據公式（1），對株洲市2012 年、2016 年及2020 年的供應鏈生態系統韌性進行評估，構建3 個年份下16 個指標的矩陣Rmn；

2）依據公式（2）（3）及從優隸屬度原則構建矩陣；

3）依據公式（4）構建矩陣RΔ；

4）依據公式（6）構建歸一化矩陣B，并依據公式（7）—（9）計算，并得到演化動力及網絡結構的各評估指標的熵和熵權（見表3）；

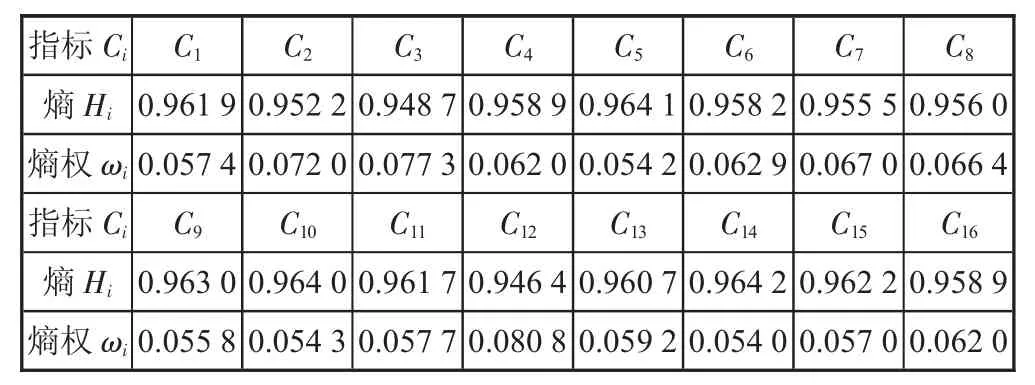
表3 供應鏈生態系統韌性評估指標權重

5）計算貼近度。根據公式計算得出株洲市3 年的供應鏈生態系統韌性的綜合歐式貼近度ρHj。

三年來，株洲市供應鏈生態系統的韌性不斷提高，各項指標數據也都保持增長的態勢，但從事交通運輸、倉儲和郵政業的物流作業人員在下降，同時這一方面的固定資產投資則保持著不斷上漲的態勢，分析可能是由于智能化賦能產業升級，解放了過多的勞動力成本；從制造業來看，制造業從業人員逐年增加，規模工業企業個數也不斷增加，為了獲取更大的市場份額，各工業企業在研發支出上不斷增加。

3 結語與建議

本研究從內外兩方面探究株洲市制造業供應鏈生態系統演化動力，以尋找適配于株洲市自身發展情況的網絡韌性指標和演化動力因素，確定韌性評估指標體系并構建韌性評估模型，從而對系統韌性進行評估與分析，最后根據分析的結果，提出韌性提升對策：

1）生態系統演化動力方面。要促進供應鏈系統演化的動力，需要從系統的內外兩個方面出發，從內部而言，要發掘人才，興辦實體制造業，并加強生產制造的配套的物流企業；從外部而言，要加強道路建設，聯通企業與企業，城市與城市。

2）生態系統網絡結構方面。要建設區域性的大企業，加強節點企業的規模大小，促進企業間的密切貿易供應關系，同時通過招商引資，多引入外省乃至外資制造業落戶本地，增大網絡密度。