控制工程中MATLAB 的時域分析與根軌跡繪制應用探究

吳 理， 李自成，2， 羅敬崴， 劉曾杉， 申啟俊

（1.成都理工大學工程技術學院， 四川 樂山 614000； 2.核工業西南物理研究院， 四川 成都 610000）

0 引言

時域分析法利用對系統的微分方程式及時間傳遞函數，進行拉普拉斯轉換求得系統實際輸出的表達式。根據給出的信息可以計算得出控制器的時間響應,然后再利用響應圖來解析控制器的特性。但是在這中間的處理過程中需要較大的運算量，而且既耗時又費腦。根軌跡分析法理解控制系統的圖解方法更加便捷，于是就需要利用MATLAB 軟件分析控制的性能指標，并通過繪制系統的階躍信號響應曲線圖與根軌跡簡潔直觀的顯示出來。使用SimuLink 對系統進行建模與仿真避免在實際工程應用中產生問題。

1 線性定常系統的時域響應

線性系統的時域分析法在自動控制系統中，對于線性定常控制系統，根據系統的運動規律與特點，可利用時域分析法去分析控制系統的性能。通過微分方程便可以求出系統的動態性能指標。

數學模型對任何系統進行分析都需要先進行建立，系統數學模型是針對各變量間相互作用和變化規律的數學描述。在自動控制系統中，建立這種模型是系統分析的基礎。MATLAB 提供了多種工具和函數，用于創建控制系統的數學模型，包括傳遞函數、零極點增益和狀態空間模型。這些模型有助于理解系統特性，選擇合適的控制策略，并優化系統性能。

本文只對傳遞函數模型進行研究，某輸入輸出分別用U（t）、Y（t）來表示，并且它是單輸入單輸出系統，其線性系統的傳遞函數模型則為：

MATLAB 控制工具箱中提供了tf（）函數，該函數允許使用多項式系數來表示分子和分母，從而建立傳遞函數。這個功能有助于快速構建控制系統模型，以便進行進一步的分析和設計，其常用的調用格式為：

用MTALB 表示傳遞函數：

根據多項式系數求出傳遞函數模型的程序如下：

運行結果如下：

二階控制系統是以二階微分方程表示的控制系統，其中包括二個儲能單元。電能在二個單元間傳遞，使其產生來回振蕩的趨勢。當阻尼值比較小時，系統就產生振蕩特性。因此二階系統在控制工程中運用很普遍，如電磁技術中的RLC 控制系統、機械系統中的彈簧、質量、阻尼系統，同時，在一定條件下的許多高階系統，可以類似為二階系統來研究。因此本文選擇二階系統展開研究。

以二階系統為例介紹動態性能指標，二階系統的動態性能指標主要有：上升時間tr、峰值時間tp、最大超調量Mp，延遲時間td、、調節時間ts。

典型二階系統的結構圖如圖1 所示。

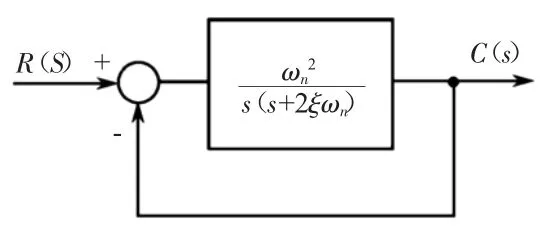
圖1 典型二階系統的結構

其閉環傳遞函數為：

式中：ξ為系統的阻尼比；ωn為系統的無阻尼自然振蕩角頻率為系統振蕩周期。

使用MATLAB 繪制出頻率ωn=3，阻尼比ξ=0，0.2，0.4，…，1.0，2.0 時的單位階躍響應曲線圖，程序如下：

如圖2 所示，從圖中分析可以得出：

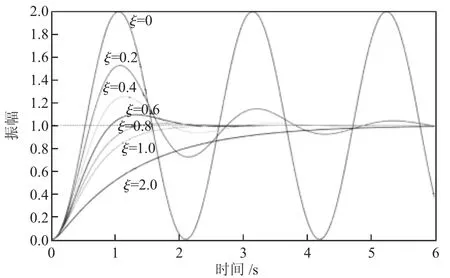
圖2 不同阻尼的階躍響應曲線圖

ξ=0 時，系統為無阻尼狀態，響應曲線等幅振蕩。

0＜ξ＜1 時，系統為欠阻尼狀態，阻尼比越大，響應曲線振蕩減小，超調量也呈減小趨勢，系統的穩定性也越好。

ξ=1 時，系統為臨界阻尼狀態，響應曲線呈單調上升趨勢，沒有超調量。系統穩定性好

ξ＞1 時，系統為過阻尼狀態，響應曲線呈緩慢上升趨勢，沒有超調量。系統穩定性好。

2 線性定常系統的穩定性

負半平面左側全是該系統的微分方程的特征方程的根，或者系統的傳遞函數的極點都不位于右半平面，是一個線性控制系統保持穩定的充要條件。

已知系統的傳遞函數為：

在MATLAB 控制工具箱中提供了roots()函數，可用于直接計算多項式根，其常用的調用格式為：

應用roots()函數求解特征根時，如果特征多項式中缺少某次冪的項，那么在使用這個函數時，需要在對應的位置添加上系數0。

根據特征多項式，判斷系統的穩定性需要求其特征根。程序如下：

運行后，其特征根如下：

通過上面的特征根的值可以看出只有負實部的特征根，故此系統是穩定的。

MATLAB 除了利用上面的求出特征根的方式來判斷系統的穩定性還可以使用零極點圖來判斷系統的穩定性。

程序如下：

運行后，零極點即增益的值如下：

零極點如圖3 所示。

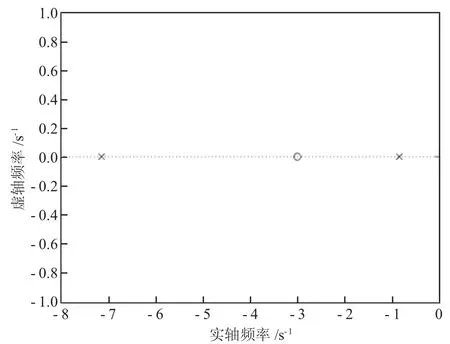
圖3 零極點圖

3 控制系統時域響應的性能指標

已知系統的傳遞函數：

對于這個二階系統的節約響應進行評估，使用MATLAB LTI Viewer 工具箱可以便于直觀地研究系統性能指標，具體操作步驟如下。

在MATLAB 程序中建立二階系統閉環傳遞函數模型G。

在MATLAB 控制工具箱中提供了step()函數，可用于直接繪制動態系統的階躍響應圖，其常用的調用格式如下：

完整程序代碼如下：

在命令行界面輸入ltiview，即可啟動LTI Viewer工具箱。

在“File”菜單中，選擇“Import”，然后再導入系統數據對話框中[2]，將上面創建的傳遞函數模型導入工作區域，從而獲得系統單位階躍響應曲線，如圖展示。

在”File”的下拉菜單中選擇“Page Setup”選項，可以對系統仿真時的打印輸出和顯示界面進行設置。

從圖4 中可以得出在2.21 s 時，響應曲線達到頂峰，隨后時間延長，曲線逐漸下降。繼續增加時間，曲線呈現波動上升和下降的趨勢，最終在3.4 s 時穩定。通過在曲線上右鍵單擊，可以獲得系統的性能指標：上升時間為tr=1.04 s，峰值時間為tp=2.21 s，ts=3.4 s。這表明，利用MATLAB 可以迅速、準確地從響應曲線中提取性能指標。

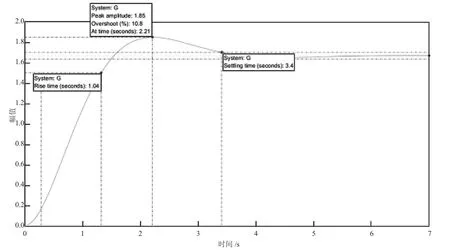
圖4 階躍響應曲線

4 Simulink 建模與仿真

Simulink 是MATLAB 核心組件之一，它能提供動態系統建模、仿真及進行分析。無需人來編寫大量代碼，只需要使用鼠標的操作，便可輕松地構建出復雜的系統。

Simulink 具有廣泛的應用范圍，其結構和流程清晰，仿真精確并且符合現實規律，具有高效能和敏捷性等優點。因此，Simulink 已在控制理論復雜仿真和設計中得到廣泛應用。同時，Simulink 可以和許多第三方軟件和硬件配合使用

用MATLAB 仿真與分析控制系統的步驟如下：

1）建立模型并確定仿真的輸入輸出參數；

2）設置仿真參數；

3）進行動態仿真并檢查輸出結果。

在此，使用Step 模塊產生單位階躍信號，比較環節采用Sum 求和模塊，使用TransferFun 模塊構造雙擊模塊打開對話框設置Numerator 分子參數［35］，Denominator 分母參數［1 2 0］，校正環節也使用TransferFun 模塊進行相對應的設置，使用Bus Creator 模塊將三個輸出信號合并成一個信號這樣就可以在一個圖像下顯示出三個信號，方便進行比較觀察，輸出階躍響應用Scope 示波器模塊，仿真模型如圖5 所示。

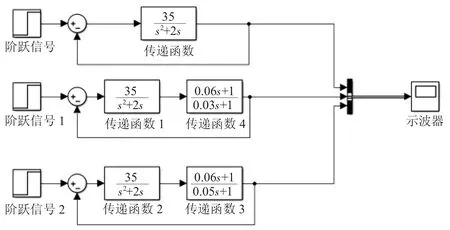
圖5 SimuLink 仿真圖

運行仿真前需要設置好仿真參數，顯示系統的單位階躍響應曲線需要雙擊Scope 模塊。如圖6 所示。

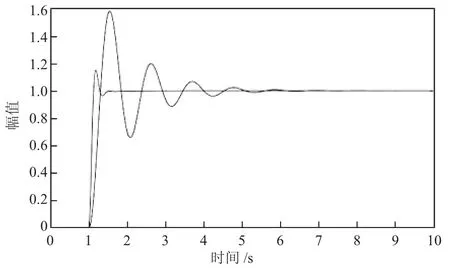
圖6 Scope 顯示波形圖

5 根軌跡分析

控制系統的快速性、準確性、穩定性等問題，主要根據s 平面上系統的特征根的分布情況來判定，但是直接求取高階系統的開環零極點很不容易，根軌跡法作為一種圖解法，它不直接求解[1]。

閉環控制系統的準確性和穩定性主要取決于系統的閉環極點在s 平面上的分布。然而，對于高階系統，特別是在系統分析和設計時，確定閉環極點是一個具有挑戰性的任務，尤其是在系統分析或設計時，特征根的變化受到某些參數的影響，采用直接求根的方法就顯得十分繁瑣，難以實際應用。繪制系統的根軌跡可以通過自動控制原理的基本規則來進行粗略的繪制。

繪制根軌跡步驟如下：極點和零點；起點和重點；實軸區域的根軌跡；漸近線；分離點；入射角和出射角；虛軸交點。

上述幾條規則雖然是人工繪制根軌跡的繪制步驟，但是人工繪圖極為麻煩，正確率差，計算步驟較多，計算量大。并且在傳遞函數中的零極點如果發生改變，根軌跡的圖也會隨之改變，又得重新繪制圖形。此時直接在MATLAB 軟件的命令行中輸入系統的傳遞函數，使用MATLAB 控制工具箱中的rlocus()函數，只需要編寫幾行代碼繪制出根軌跡圖的優勢就凸顯出來了[3]。其常用的調用格式如下：

已知系統的傳遞函數為：

用MATLAB 繪制系統的根軌跡圖。

完整的程序代碼如下：

運行結果如圖7 所示。

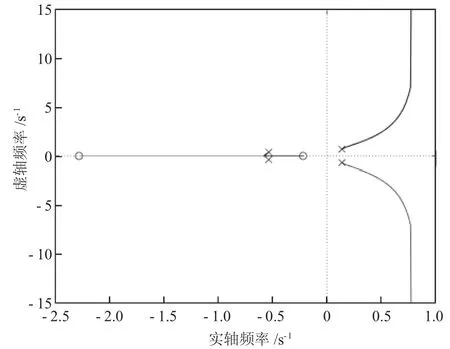
圖7 根軌跡圖

6 結語

傳統的人工計算方法求解階躍信號響應，穩定性、性能指標、穩態誤差等這些問題計算非常的繁瑣，本文根據系統的傳遞函數編寫MATLAB 程序，便可以非常簡單得到系統的階躍響應圖形，利用函數不需要人來進行計算便能判斷出系統的穩定性，并根據圖形分析控制系統的性能順便得到系統的性能指標，使用Simulink 建模與仿真不需要實物，在系統中直接使用拖放式操作，方便簡單地建立起直觀的仿真模型。直接在電腦上就能進行分析，還可以看出利用Matlab可以更加形象生動的表現了系統的各種特性，并且加快了分析速度。