核心素養(yǎng)視域下“5E”學(xué)習(xí)環(huán)在數(shù)學(xué)教學(xué)中的應(yīng)用研究

牛偉琪

［摘? 要］ 核心素養(yǎng)視域下的數(shù)學(xué)教學(xué)，如何利用好“5E”學(xué)習(xí)環(huán)提高教學(xué)效率，促使學(xué)生深度學(xué)習(xí)的發(fā)生呢？研究者從“5E”學(xué)習(xí)環(huán)的概述出發(fā)，以“平行四邊形的面積”教學(xué)為例，分別從課堂的“借助情境，引入新知”“呈現(xiàn)任務(wù)，探索新知”“成果展示，解釋新知”“練習(xí)拓展，遷移新知”“多元評價，完善新知”等環(huán)節(jié)開展教學(xué)與思考，與同行交流。

［關(guān)鍵詞］ “5E”學(xué)習(xí)環(huán)；核心素養(yǎng)；探究

實踐證明，將“5E”學(xué)習(xí)環(huán)模式應(yīng)用到小學(xué)數(shù)學(xué)教學(xué)中，不僅能幫助學(xué)生掌握好“四基與四能”，還能發(fā)展其“三會”能力，有效促進(jìn)其數(shù)學(xué)核心素養(yǎng)的發(fā)展。因此，筆者以“平行四邊形的面積”教學(xué)為例，具體談?wù)勅绾螒?yīng)用“5E”學(xué)習(xí)環(huán)提升教學(xué)效率和發(fā)展學(xué)生核心素養(yǎng)。

一、“5E”學(xué)習(xí)環(huán)的概述

“5E”學(xué)習(xí)環(huán)是一種以“概念轉(zhuǎn)變理論、建構(gòu)主義理論、探究式教學(xué)”為理論基礎(chǔ)自然發(fā)展起來的產(chǎn)物，對理科教學(xué)有著重要價值與指導(dǎo)意義。如表1，“5E”學(xué)習(xí)環(huán)由“引入、探究、解釋、遷移、評價”五個環(huán)節(jié)組成，每個環(huán)節(jié)對應(yīng)不一樣的教學(xué)目標(biāo)，對教師與學(xué)生分別提出不同的要求。

二、具體措施

1. 借助情境，引入新知

課堂伊始，教師首先要思考如何調(diào)動學(xué)生學(xué)習(xí)的積極性與主動性？創(chuàng)設(shè)豐富的教學(xué)情境往往能快速吸引學(xué)生的注意力，激發(fā)學(xué)習(xí)的內(nèi)驅(qū)力，為后續(xù)的探究活動奠定基礎(chǔ)。實踐證明，有效的情境不僅能引發(fā)學(xué)生的好奇心，激發(fā)認(rèn)知沖突，還能讓學(xué)生在“憤、悱”的狀態(tài)下調(diào)動學(xué)習(xí)積極性。

本節(jié)課，應(yīng)用“5E”學(xué)習(xí)環(huán)模式執(zhí)教“平行四邊形的面積”，教師要在“5E”的“引入”環(huán)節(jié)結(jié)合學(xué)生認(rèn)知特征與興趣點創(chuàng)設(shè)能激趣啟思的教學(xué)情境，以揭示新知，為后續(xù)的探究活動奠定基礎(chǔ)。

“吸管”是學(xué)生經(jīng)常接觸的生活用品，教師可在引入環(huán)節(jié)借助吸管這個生活實際物品創(chuàng)設(shè)情境：用吸管制作長方形，通過對長方形的拉動，引起學(xué)生的視覺沖突。

師：觀察發(fā)現(xiàn)，因吸管制作的長方形經(jīng)過輕輕拉動就變成了一個平行四邊形，你們覺得拉動前后兩個圖形的面積一樣嗎？

面對這個問題，學(xué)生呈現(xiàn)出不一樣的答案。顯然，這個情境成功引發(fā)了學(xué)生的認(rèn)知沖突，有效激發(fā)了學(xué)生的探索欲。

師：變形前后兩個圖形的面積之間存在什么關(guān)系嗎？如果要計算平行四邊形的面積，該怎么辦呢？

在問題的啟發(fā)下，學(xué)生表現(xiàn)出濃厚的探索興趣，教師可趁機引出本節(jié)課的教學(xué)主題——平行四邊形的面積。由此可見，情境引入具有激趣與揭示教學(xué)主題的作用，對增強教學(xué)效果具有重要意義。

2. 呈現(xiàn)任務(wù)，探索新知

在探究環(huán)節(jié)，教師的任務(wù)是提出探究任務(wù)并為學(xué)生提供充足的探索空間；學(xué)生的任務(wù)是把握住探究的機會，充分發(fā)揮學(xué)習(xí)的主觀能動性，通過對系列探究活動的分析與思考自主提出新的想法，同時將已有的認(rèn)知遷移到探究過程中，為構(gòu)建新知奠定基礎(chǔ)。在此過程中，教師應(yīng)關(guān)注學(xué)生在課堂中的一言一行，做好引導(dǎo)與點撥工作，讓探究活動順利進(jìn)行。

“讓學(xué)生親歷平行四邊面積公式的推導(dǎo)過程”為本節(jié)課教學(xué)的重點與難點，也是探究的核心。因此，筆者提出三個探究任務(wù)。

探究1：在學(xué)生獨立思考的基礎(chǔ)上進(jìn)行小組合作學(xué)習(xí)，分析任意一個平行四邊形可轉(zhuǎn)化成什么圖形？

學(xué)生從自身原有的認(rèn)知結(jié)構(gòu)出發(fā)，結(jié)合平行四邊形的性質(zhì)與特點進(jìn)行圖形轉(zhuǎn)化，然后與同伴分享自己的想法。互動中，學(xué)生各抒己見，探索氛圍和諧、民主。

探究2：學(xué)生根據(jù)自己的想法，以動手操作的方式將一個平行四邊形轉(zhuǎn)化為一個長方形。

學(xué)生取出課前用卡紙自制的平行四邊形，通過畫、剪、拼等方式進(jìn)行圖形的轉(zhuǎn)化。（教師巡視）

探究3：雖然學(xué)生轉(zhuǎn)化圖形的方法各異，但是都成功了。將轉(zhuǎn)化前后的兩個圖形放在一起進(jìn)行對比，它們之間有什么關(guān)系？

學(xué)生思考并交流，各組學(xué)生通過對轉(zhuǎn)化前后圖形的觀察、對比、分析，逐步獲得統(tǒng)一的結(jié)論。隨著一個個探究任務(wù)的提出，學(xué)生積極思考，經(jīng)過“做中學(xué)”，親歷了圖形轉(zhuǎn)化的過程，有效提升了動手操作能力、直觀想象能力、抽象能力等。探究活動基本遵循了先獨立分析、后合作交流的模式，學(xué)生將個人的智慧融入集體中，在通力合作中協(xié)同共進(jìn)。

3. 成果展示，解釋新知

此為“5E”學(xué)習(xí)環(huán)的中間環(huán)節(jié)，著重關(guān)注學(xué)生規(guī)范、科學(xué)的理解與解釋新知的情況。教師在此環(huán)節(jié)要為學(xué)生提供充足的時間與空間，為學(xué)生的思維搭建“腳手架”，鼓勵學(xué)生將探究結(jié)論展示出來，并盡可能應(yīng)用規(guī)范、完整的數(shù)學(xué)語言來解釋與描述；同時，教師要有針對性地對學(xué)生的解釋加以點撥與引導(dǎo)，讓學(xué)生從真正意義上掌握新知，夯實探究成果。

當(dāng)學(xué)生順利完成三個探究任務(wù)后，教師可鼓勵學(xué)生自主將組內(nèi)探究成果借助多媒體設(shè)備進(jìn)行投影展示，各小組呈現(xiàn)的方法不一樣。

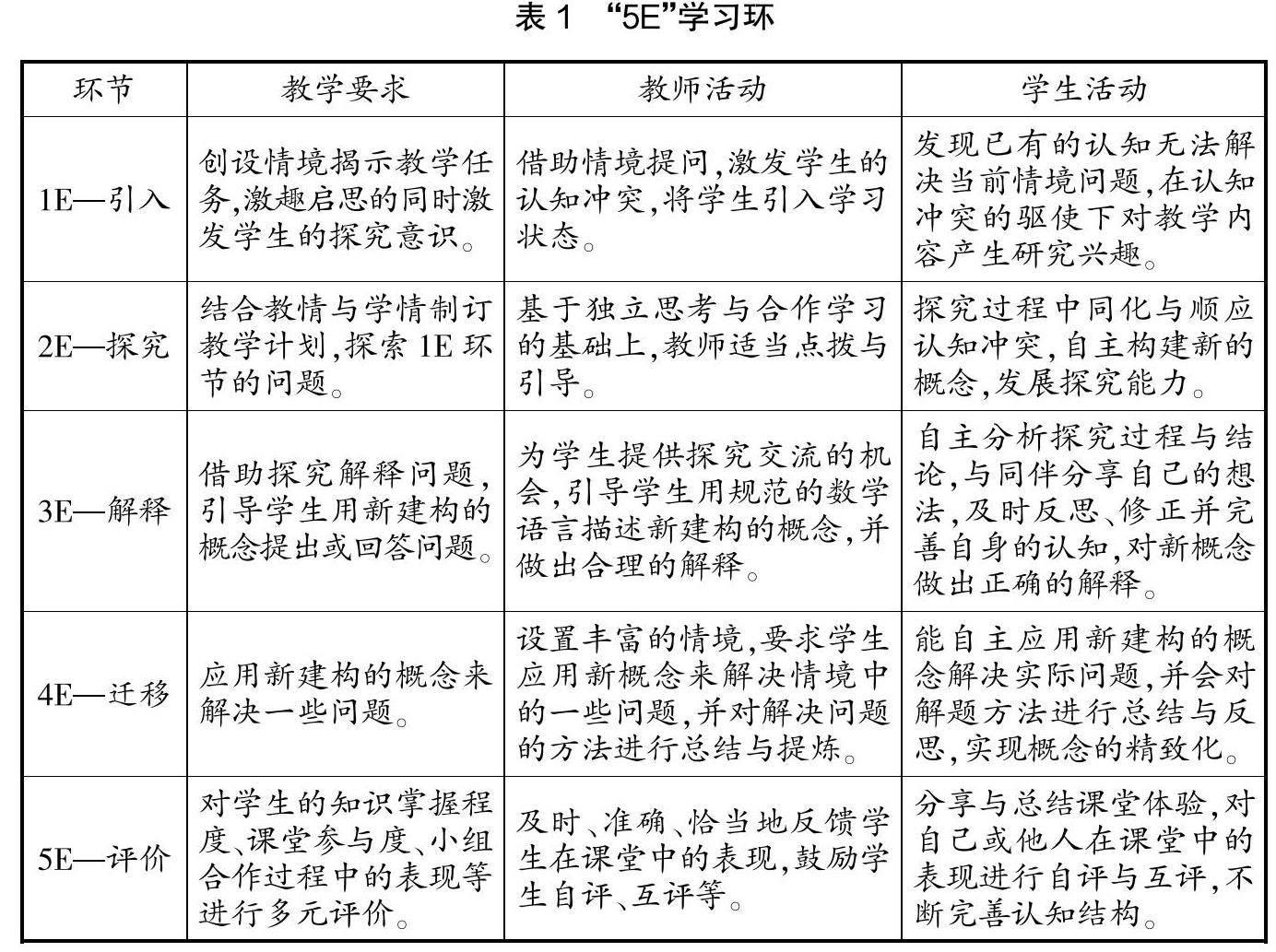
方法1：剪下過平行四邊形頂點的高（見圖1），把剪下的直角三角形和直角梯形拼接到一起，形成長方形。

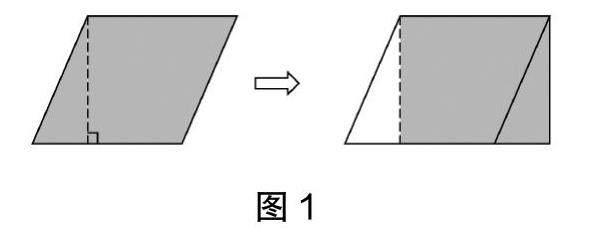
方法2：如圖2，剪下平行四邊形的任意高，將獲得的兩個直角梯形進(jìn)行拼接形成長方形。

方法3：剪下過平行四邊形斜邊中點的高（見圖3），將獲得的兩個小直角三角形拼接到剩下的圖形上，形成長方形。

師：觀察這三種拼接方法，可見轉(zhuǎn)化前后的圖形之間有哪些條件發(fā)生了改變，哪些條件沒有發(fā)生變化？

生：圖形形狀都由平行四邊形轉(zhuǎn)化成了長方形，即形狀發(fā)生了改變，但不論用哪種剪拼方式，圖形的面積是恒定不變的。

“變與不變”的原理在學(xué)生的自主操作中自然生成，據(jù)此師生共同推導(dǎo)出平行四邊形的面積計算公式。此過程，學(xué)生通過動手操作、動腦思考，由淺入深地掌握了平行四邊形的面積計算公式，并提煉出一種重要的數(shù)學(xué)思想——轉(zhuǎn)化思想。此過程可發(fā)展學(xué)生語言表達(dá)能力和邏輯推理能力等。

4. 練習(xí)拓展，遷移新知

該環(huán)節(jié)的關(guān)鍵在于讓學(xué)生通過解決問題來實現(xiàn)知識的遷移，不斷鞏固對新知的認(rèn)識。教師可根據(jù)學(xué)生的認(rèn)知水平來組織課堂練習(xí)，帶領(lǐng)學(xué)生結(jié)合知識間的聯(lián)系進(jìn)行知識的拓展與研究，達(dá)到遷移新知與強化認(rèn)知的效果。

練習(xí)訓(xùn)練是遷移新知的重要途徑之一。隨著系列探究活動的開展，學(xué)生獲得的體驗各不一樣，因此對新知也會形成不同程度的認(rèn)識。學(xué)生的個體差異是教師設(shè)計練習(xí)的主要依據(jù)，教師可結(jié)合學(xué)情設(shè)計分層練習(xí)，讓每個學(xué)生都擁有思維訓(xùn)練的機會。本節(jié)課，筆者設(shè)計了基礎(chǔ)練習(xí)、提高練習(xí)和拓展練習(xí)。

（1）基礎(chǔ)練習(xí)

如圖4，請分別計算圖中兩個平行四邊形的面積。

（2）提高練習(xí)

校園內(nèi)有一個平行四邊形的花圃，其面積為36m2，高為6m，求該花圃的底邊長度。

（3）拓展練習(xí)

如圖5，為了便于小區(qū)內(nèi)人員的出行，物業(yè)中心準(zhǔn)備在小區(qū)綠化帶中鋪設(shè)一條平行四邊形的鵝卵石小路，施工單位提供了三種鋪設(shè)方案，哪種方案用到的鵝卵石數(shù)量最少？

以上三個由淺入深的問題，為每個學(xué)生提供了思考的機會，學(xué)生嘗試應(yīng)用剛建構(gòu)的新知來解決這些問題。學(xué)生解題后，教師可擇取一些具有代表意義的結(jié)論進(jìn)行展示交流。

此過程，學(xué)生不僅學(xué)會了應(yīng)用新知解決問題，實現(xiàn)了知識的遷移，還深化了對平行四邊形面積的理解，訓(xùn)練了思維。尤其是后兩個問題，對發(fā)展學(xué)生的“三會”能力具有重要意義。

5. 多元評價，完善新知

評價貫穿課堂教學(xué)的每個環(huán)節(jié)。在教學(xué)中教師一直在與學(xué)生積極互動、交流，其中不乏各種評價與鼓勵。恰到好處的課堂反饋與評價是引發(fā)學(xué)生積極思考、助推探究行為的催化劑，對發(fā)展學(xué)生的數(shù)學(xué)核心素養(yǎng)具有重要價值。

本節(jié)課，教師立足于學(xué)情，進(jìn)行了客觀、積極的評價。在課堂巡視時，教師充分關(guān)注了學(xué)生的思維狀況、動手能力等，并以此為依據(jù)提出相應(yīng)的問題，讓教學(xué)評價滲透在教學(xué)的每個環(huán)節(jié)。比如，為了了解學(xué)情，教師提出：“你們覺得平行四邊形的面積可能跟哪些因素有關(guān)？”“平行四邊形的高越高，它的面積就越大，對不對？”

從學(xué)生提供的結(jié)論，教師可初步判斷學(xué)生的認(rèn)知水平，并據(jù)此調(diào)整教學(xué)方案，想方設(shè)法發(fā)展學(xué)生的“四基與四能”和鞏固其認(rèn)知，為完善其認(rèn)知結(jié)構(gòu)服務(wù)。而學(xué)生在多元化評價的課堂中積極探究、樂于解釋，收獲滿滿。

三、結(jié)語

“5E”學(xué)習(xí)環(huán)的“引入—探究—解釋—遷移—評價”各個環(huán)節(jié)既獨立，又具有一定的聯(lián)系，其中評價貫穿整個教學(xué)的始末。如圖6，此為一個閉環(huán)，引入環(huán)節(jié)借助情境吸引學(xué)生的注意力，讓學(xué)生積極參與到探究中來；探究環(huán)節(jié)為解釋環(huán)節(jié)提供思路，可發(fā)展學(xué)生的創(chuàng)造意識；解釋環(huán)節(jié)進(jìn)一步完善學(xué)生對新知的理解，為知識的遷移應(yīng)用作鋪墊；遷移環(huán)節(jié)對提升學(xué)生的應(yīng)用意識與推理能力具有重要價值；評價則滲透于每個環(huán)節(jié)中。

實際教學(xué)時，教師不一定要嚴(yán)格按照各個步驟按部就班地依次進(jìn)行，可結(jié)合實際教情與學(xué)情，擇優(yōu)選擇更科學(xué)的方法促使“5E”的流動，以發(fā)展學(xué)生的數(shù)學(xué)核心素養(yǎng)。

新課改強調(diào)數(shù)學(xué)教學(xué)要關(guān)注教學(xué)理念、方法與模式的創(chuàng)新，教師應(yīng)與時俱進(jìn)加強學(xué)習(xí)，不斷積累教學(xué)經(jīng)驗，提高教學(xué)實效。“5E”學(xué)習(xí)環(huán)是一種利于學(xué)生長久發(fā)展的教學(xué)方式，與新課改發(fā)展數(shù)學(xué)核心素養(yǎng)的目標(biāo)一致，值得廣大教師去探索研究。