幾何直觀:實現小學數學深度學習的有效路徑
黃旭


[摘? 要] 充分利用幾何直觀教學可以展示知識的抽象過程,實現學生深度學習。在教學中,教師可以用幾何直觀呈現學生易犯錯誤,促進新知理解;用幾何直觀搭建思維階梯,完成釋疑解惑;用幾何直觀揭示知識聯結,建構知識網絡。
[關鍵詞] 幾何直觀;深度學習;課堂教學
幾何直觀由于具有直觀性的特征,可以很好地溝通抽象思維與信息思維、抽象的數學知識與直觀的圖形語言,可以很好地打開學生的思維閘門,促進學生對知識的深度理解。這就需要教師在實際教學中,巧妙運用幾何直觀教學引領學生自然而然地開展深度學習,從而更好地發展其數學核心素養。
一、用幾何直觀呈現易犯錯誤,促進新知理解
對數學學習而言,學生犯錯是必然的。因此在教學的過程中,教師應從具體的教學內容出發,精心設計教學過程,并借助幾何直觀呈現學生易犯的錯誤,讓學生去觀察、分析、對比和辨析,從中探尋錯因、明晰方法、領悟本質,從而促進其對新知的理解和內化數學本質。
案例1? 兩位數乘兩位數的橫式筆算
計算:14×12。
師:在學習新課之前,你們能先試著計算嗎?(在教師的鼓勵下,學生大膽嘗試,教師巡視)
師:誰愿意展示自己的方法?
生1:我是這樣計算的。首先,將14看作10與4,將12看作10與2;然后,計算4×2=8,10×10=100;最后,計算8+100=108。(出示圖1所示的方法)
師:生1的方法正確嗎?
生2:我覺得是錯誤的。
師:錯在哪里?(學生面面相覷,不知如何回答)
師:那我們就先把這個問題放一放,來學習今天的新知吧。
師:經過剛才一系列探索,我們得出了圖2所示的計算過程及結果。現在再回到學習前的問題,現在是否有了新的思路?生1,有沒有發現你錯在哪里?
生1(撓了撓頭):在計算時我僅計算了8與100這兩個部分,而40與20這兩個部分遺漏了。
生2:只要再添上10×4=40和10×2=20即可。
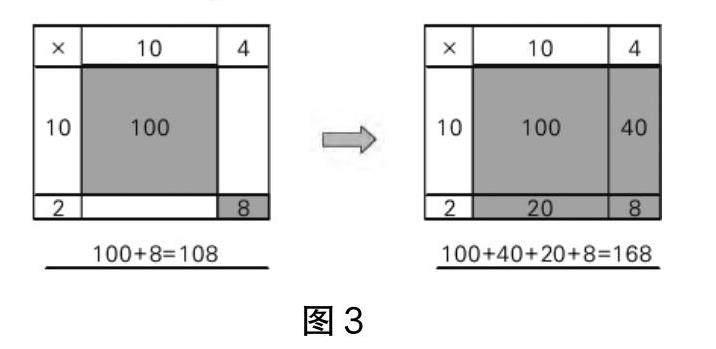
師:非常棒,你們通過觀察得到了結果,下面我們一起回顧一下(課件呈現圖3)。
以上案例中,教師利用“錯誤”這一可生成性資源,立足幾何直觀,牢牢抓住“兩位數乘兩位數的筆算”的算理,引導學生在觀察、辨析和比較的過程中經歷“犯錯—剖析—糾錯—內化”的過程,讓學生直觀地感知計算兩位數乘兩位數需包含的四個部分,從而更好地內化認識。這樣的教學過程不僅為學生進一步的探究和學習打下了基礎,還培養了學生透過想象找尋數學本質的能力。
二、用幾何直觀搭建思維階梯,完成釋疑解惑
小學生的思維呈現具體形象的特征,而數學知識的抽象性時常讓學生產生困惑。建構主義認為,數學學習不是簡單的知識傳遞,而是學生自己建構的過程。因此,教師不能直接將結果拋給學生,而應借助幾何直觀為抽象性思維薄弱的小學生搭建思維階梯,促進學生在親歷知識形成和發展的過程中逐一突破困惑,最終實現釋疑解惑,真正理解知識。
案例2? 小數乘法
師:經過剛才的計算,你認為一個乘數不變,另一乘數發生變化時積有何變化?請試著通過列舉法驗證你發現的規律。(經過探索,大部分學生有了一定的認識,但仍然有部分學生產生了疑問)
生1:從之前學習的整數乘法可以得出,積一定會等于或大于乘數。而這里的小數乘法卻有了積比乘數小的情況。比如:1.5×0.8=1.2,1.8×0.55=0.99,這是什么原因?
師:這是為什么呢?下面,請圍繞算式進行小組合作探索:1.5×1,1.5×1.4,1.5×0.8。
(學生合作學習,教師巡視)
生2:乘法的意義角度:1.5×1表示1個1.5,得到積1.5;相較于1個1.5,1.5×1.4得數大一些;相較于1個1.5,1.5×0.8得數小一些。
生3:我覺得還可以借助圖形呈現積的變化規律。
師:可以具體說一說嗎?
生3:如圖4,1.5×1=1.5可這樣表示。
師:1.5×1.4的積與乘數1.5相比如何呢?
生3:進一步作圖,該長方形的長不變,還是1.5,寬增加到1.4,可看作1和0.4的和。如圖5,將它的面積分為兩個部分,據圖可列出算式1.5×1.4=1.5×1+1.5×0.4,從而得出“其積比乘數1.5大”的結果。
師:進一步地,1.5×0.8的積與乘數1.5相比如何呢?
生3:繼續作圖探尋結果,如圖6:長不變,還是1.5,寬變成了0.8。經過思考長方形面積可用1.5×0.8表示,相較于圖4的長方形減少“1.5×0.2”,從而列式1.5×0.8=1.5×1-1.5×0.2,得數也比1.5小了。
師:看來無論是圖形構造或是計算,我們都能得出相同的結論。
生4:我們小組作出了圖7,也有了發現。
師:結合圖形得出結論,非常棒!其他組可有其他說理的方法?
生5:我們組是借助一個生活例子解釋的……
以上案例中,學生借助幾何直觀開展數學探索,通過圖形揭示知識本質,讓原本模糊的知識清晰化,讓原本抽象的道理形象化,加深了對新知的理解,也深化了自身的數學思維。
三、用幾何直觀揭示知識聯結,建構知識網絡
數學的邏輯性決定了知識間的縱橫交錯,而學生由于自身的思維特征很難融會貫通地理解知識。這就需要教師在教學過程中充分利用幾何直觀溝通新舊知識的聯系,揭示知識聯結,促進學生在深度學習中建構系統的、完善的知識網絡。
案例3? 乘法分配律
師:事實上,乘法分配律在我們學習筆算乘法時已有接觸。請試著結合乘法分配律描述圖8中豎式計算的奧秘。
生1:首先,把12看作2與10的和;然后,求得2個15是30,10個15是150;最后,求得30與150的和是180。
生2:可以先算15×2=30(2行點子數),后算15×10=150(10行點子數),最后相加即可。
師:那這個過程是否可以利用橫式表示呢?
生3:先將12行分為2行與10行;再將2與10分別去乘15,得出2行的點子數和10行的點子數;最后將這些點子數相加。事實上,不管是橫式還豎式,計算道理都是一樣,即乘法分配律。(教師出示圖9)
實踐證明,利用圖形不僅豐富了學生的認識,還深化了學生對乘法分配律內涵的理解,更幫助學生架構起多位數乘法與乘法分配律的橋梁,最終實現了新知的完整建構,發展了數學思維能力。
總之,幾何直觀可以讓復雜的問題變得形象具體,教師運用幾何直觀進行數學教學要適應小學生的思維特征。在數學教學中,教師有必要利用幾何直觀呈現學生易犯的錯誤,搭建思維階梯,揭示知識聯結,從而助力學生的深度學習,讓學生在數與形的完美統一下感悟數學思想方法,更深刻地理解數學知識內涵和發展數學思維能力。

