新黎曼理論及其應用

［摘要］新黎曼理論作為分析近現代音樂的重要方法之一，對其研究具有一定意義。本文第一部分簡要介紹了“維茲曼域”和喬茲的七和弦轉換模型，第二部分運用PLR變換模型并結合前文介紹的兩種轉換方式來分析肖邦《前奏曲Op28 No9》，并從新黎曼理論視角闡釋和弦的相互關系。在分析過程中，筆者還嘗試仿照“維茲曼域”構建減三和弦的轉換路徑并分析作品片段，試圖豐富新黎曼理論分析模型。

［關鍵詞］新黎曼理論;和弦轉換;

［中圖分類號］J614.1［文獻標識碼］A［文章編號］1007-2233（2024）04-0116-03

［收稿日期］2023-11-01

［作者簡介］（朱越（2001—），女，安徽師范大學作曲技術理論方向碩士研究生。（蕪湖241000） ）

一、理論介紹

新黎曼理論是一種用數學模型模擬和弦關系的轉換方法，源于大衛·列文（David Lewin）的《一種形式化的廣義調性功能理論》，該理論最重要的內容即PLR轉換模型和音網，具體內容此處不再贅述，本文將介紹在此理論上衍生的兩個概念。

（一）維茲曼域

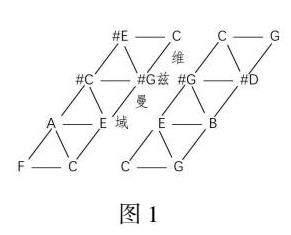
1853年，卡爾·維茲曼（Carl Weitzmann）對增三和弦作出了系統解釋。他認為有16 種通過聲部間的半音將一個增三和弦與大三或小三和弦連接起來的方式。在此基礎上，理查德·科恩根據增三和弦可以將八度均等劃分以及可以通過“最儉省的聲部進行”產生多個協和三和弦的性質將“維茲曼域”作為構建三和弦轉換關系的重要基礎。這一理念的提出，將增三和弦納入新黎曼理論的討論范圍，擴充了該理論的模型。由于音網的右斜方向是按大三度排列的，所以每一條右斜方向的線條都能夠構成增三和弦，將這條邊拉開，便形成增三和弦的空間，也就是科恩文中提到的“維茲曼域”（見圖1），該區域只需變動一個音即可實現三和弦的轉換。

（二）艾德里安·喬茲七和弦模型

艾德里安·喬茲（Adrian Childs）在《Moving beyond Neo-Ｒiemannian Triads： Exploring a Transformational Model for Seventh Chords》中提出了大小七和弦以及半減七和弦的轉換模型，在這個模型中喬茲列舉出了4-27集合級之間所有可能的兩音變動也就是P2（Perturb）關系。

喬茲規定了兩種變換系統S（Similar）和C（Contrary），如譜例1所示。S指保留和弦中的兩個音，另兩個音做同向半音運動，因此以Similar為名，縮寫為S。在S的右下方標有數字，前一個數字表示保持音之間的音程級（interval class），后一個括號中的數字表示攝動兩音之間的音程級。C指保留和弦中的兩個音，另兩個音做反向半音運動，因此以Contrary為名，縮寫為C。其數字標記和S同理。在P2關系中，根據排列組合原理，C轉換應當和S轉換一樣有6種，但是有些組合在C轉換后不能構成三度疊置的七和弦，所以不計入該轉換系統內。

2譜例1中，“＋”代表大小七和弦，“－”代表半減七和弦，字母即和弦根音，例如“F＋”即為F大小七和弦，“F－”即為F半減七和弦。空心音符代表被保持，實心音符代表被彈奏。通過譜例1可以看出，S轉換改變和弦性質，C轉換保持和弦性質。除此之外，S轉換還有著和PLR轉換共同的特點——對合性。

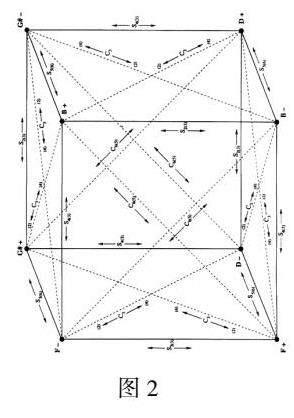
這種轉換也可以形成類似三和弦音網的轉換網絡，如圖2所示。圖中是一個三維立方體轉換模型，立方體的八個頂點分別代表一個4—27的集合成員，這八個和弦的音屬于同一個八聲音階音集。棱長和面對角線代表轉換路徑，其中棱長涉及三種S轉換，面對角線（虛線）涉及三種C轉換，通過這些轉換，每個和弦可以直接與除自身外的六個和弦形成聯系，也就是說只有一個和弦不能同原和弦形成直接轉換，這個和弦與原和弦所在的頂點相對，兩頂點相連即為立方體的體對角線（例如“F－”頂點與“D＋”頂點）。 這個模型中可以形成兩個循環，S2（3）、S5（6）循環和S4（3）、S5（6）循環，這兩個循環包含了模型中所有八個和弦。

二、實例分析

這一部分，筆者將用上述PLR轉換概念對肖邦《前奏曲Op28 No9》進行分析和總結其在新黎曼三和弦轉換理論視角下的特點。此外，筆者還嘗試模仿增三和弦“維茲曼域”構建減三和弦分析路徑并通過實例分析驗證其可行性。

肖邦《前奏曲Op28 No9》為簡單的一部曲式，劃分為三個樂句，曲式結構如圖3所示。

（一）RL/LR鏈的局部運用

RL循環為RL的復合，這種轉換需通過十二次可以形成一次循環，每次轉換不改變和弦性質。在這部作品中，出現了不完整的RL和LR鏈，分別在作品的第1、2、3、10小節。

譜例2為作品的前三小節，其和弦標記在譜例下方。第一小節后三拍的和弦B＋、E＋、A＋形成連續的RL轉換，連續上四度移位，將剛剛確立的調性模糊。

第二至第三小節的#G－、#C－、#F－、B＋屬于連續的LR轉換但略有不同。前三個和弦之間的轉換關系均為LR，如果第三個和弦到第四個和弦也是LR的話，最后一個和弦應該是B－，但是在譜例中是B＋，說明最后兩個和弦#F－與B＋的轉換在LR的基礎上復合了P轉換（在LR前后均可）。

（二）調性布局的PL鏈

正如調性關系是高一級的和弦關系一樣，三和弦轉換的循環原理在更高一級的調性層面上也是適用的，如上圖所示，該作品的調性布局為E—C—bA—E—F—E，F大調所處的位置類似E大調之間的輔助性調性，在分析時忽略不計，這樣就只剩下了E—C—bA—E，這種連續下行大三度的調性布局形成一個循環，這正是上文提到的增三和弦的特質，也屬于童忠良老師在《近現代和聲的功能網》中提到的大三度循環。當我們采用新黎曼三和弦轉換理論來分析，該作品的調性布局構成了PL循環，該循環在音網中形成的空間如圖4所示。

PL循環由PL兩個變換復合而成，其循環周期為三次，產生三個同性質的三和弦，相鄰之間為T4移位關系，若將PL拆開來看，PL的交替式變換要經過六次才能完成一次循環，每次變換產生的和弦性質都不同。上例中提到的E＋、C＋、bA＋、E＋正屬于PL循環關系，這種循環在保持一個共同音的情況下，另兩個聲部均做半音運動，這個模型解釋了浪漫主義時期半音化和聲，轉換形成的根音關系也與浪漫主義時期作曲家偏愛三度關系契合。

（三）七和弦之間的轉換

作品第四小節后兩拍的兩個和弦分別是#D半減七和弦以及B大小七和弦（見譜例3），從調性和聲角度解釋二者分別為E大調導七和弦與屬七和弦。而這兩種和弦剛好屬于上文介紹的艾德里安·喬茲七和弦模型，下面筆者將嘗試用這個模型分析聲部的運動軌跡。

通過喬茲的模型可以了解到，S和C都是以保留兩個共同音為前提的轉換，譜例中的兩個和弦有三個共同音，那么參照PLR復合鏈，可以推測應該是采用了復合轉換。上文中還提到，S轉換改變和弦性質、C轉換不改變和弦性質，而譜例中的兩個和弦性質不同，由此可以排除只含有C轉換的復合轉換。經過嘗試，筆者找出這兩個和弦在此模型下的轉換方式為S3（4）·C3（4）（見圖5），#D半減七和弦先通過S3（4）保持#D、#F兩音，A與#C下行半音到bA和C，過渡到bA（#G）大小七和弦，然后通過C3（4）保持#D、#F兩音，bA和C做反向半音運動分別到A、B兩音到達B大小七和弦。與功能和聲的解釋相比，用這種模型解釋好像麻煩許多，由于這種模型只適用于半減七和弦和大小七和弦之間的轉換，筆者目前沒有找到合適的譜例，今后筆者會繼續尋找適合的譜例。

（四）對減三和弦的界定

在這部作品中出現的七和弦有三類：一類是大小七和弦，在分析時將七音省略把其當成大三和弦看待；還有兩類是減七和弦和半減七和弦，不管省略哪個音，都會簡化成減三和弦。從筆者目前掌握的資料來看，減三和弦在新黎曼三和弦轉化體系中似乎未曾提及。受上文中“維茲曼域”的啟發，筆者嘗試仿照增三和弦的“維茲曼域”，試圖為減三和弦的轉化找到較為合理的解釋。

之所以仿照“維茲曼域”，是因為音網的構造。在音網中，右斜方向的連續大三度構成增三和弦，相應地，左斜方向的連續小三度構成了減七和弦，而且減七和弦有著和增三和弦一樣的八度均分特質，只不過減七和弦把八度均分成四份。在三和弦轉換網絡中，我們不得不將減七和弦簡化成減三和弦，通過觀察可以發現，減三和弦在音網中也可以作為中心構成儉省聲部進行或者起到過渡的作用。在保持兩個音的情況下，減三和弦有四種轉換的可能，有的移動半音，有的移動全音。例如C減三和弦，若保持C和bE兩音可以通過bG音移高全音和移低半音轉換到bA大三和弦和C小三和弦，保持bE和bG兩音則可以通過C音移低半音和移低全音轉換到bC大三和弦和bE小三和弦。

作品第7小節屬于穿越減三和弦區域的運動（見譜例4），第一拍和第三拍的和弦A＋與bB－之間為#C減七和弦，我們可以把這個和弦簡化為bB（#A）減三和弦。在音網中，A＋和bB－分別處于bB（#A）減三和弦構成的區域兩側，這兩個和弦在保持共同音的基礎上通過bB（#A）減三和弦連接，如圖6所示。

圖中左側是常規的音網，右側是將簡化后的#C減七和弦所在的左斜線條拉開后的音網，中間的區域便是減三和弦的地帶。通過音網可以清晰地觀察到，若將第二拍的減七和弦忽略，那么A＋與bB－的轉換則屬于上文中提到的保留一個共同音的PL關系，即以#C（bD）為倒影軸的轉換。當我們把減三和弦列入考慮范圍時可以發現，從A＋到#A減三和弦的轉換為保持兩個共同音，另外一個音A做上行半音運動到#A。從bB（#A）減三和弦到bB－的轉換同樣是保持兩個共同音，另一個音E上行半音到F，整個運動都屬于儉省聲部進行。不難發現，第二種解釋方式的半音運動更多，保持了更多的共同音，更加平滑，因此驗證了減三和弦加入新黎曼三和弦的轉換可行性。

結語

本文在PLR轉換模型基礎上介紹了“維茲曼域”和喬茲的七和弦轉換模型，并嘗試用其進行分析譜例。通過分析不難發現，該理論在解釋浪漫主義時期調性擴張高度半音化的作品有著突出的優勢。然而，這種分析理論的使用范圍有一定局限性，例如PLR轉換只限于大小三和弦，盡管“維茲曼域”將增三和弦納入和弦轉換的范圍，但是仍無法解釋三和弦與七和弦的轉化，在分析譜例時，七和弦都要省略某個不重要的音，將其轉換成三和弦才能進行分析，但這種分析難免會以偏概全，在面對這樣的情況時，應該與其他分析理論相結合，在最大限度地保留作品完整性的前提下進行分析。

參考文獻：

[1］理查德·科恩.唐小波，高拂曉.“新里曼”理論導論： 一次調查與一次歷史的縱覽[J.中央音樂學院學報，2017（1）：125-135.

[2］譚森.三和弦變換之視角及其技術探析[J.天津音樂學院學報，2022（1）：74-88.

[3］高暢.新里曼理論三和弦轉換的基本模式及其擴展[J.音樂探索，2015（4）：53-65.

[4］李天然.論新里曼分析法在音樂分析中的實踐意義——以勃拉姆斯《第二交響曲》第一樂章為例[J.黃鐘（武漢音樂學院學報），2022（4）：95-107;166.

[5］譚森，賈達群.三和弦變換及其結構組織手法——新里曼理論視域下的舒伯特《降E大調鋼琴三重奏》第一樂章探究[J.北方音樂，2023（2）：72-85.

[6］高暢.三和弦的逆行倒影鏈和移位鏈操作及不同轉換模式的循環[J.星海音樂學院學報，2016（2）：92-105.

[7］Adrian P. Childs，Moving beyond Neo-Riemannian Triads： Exploring a Transformational Model for Seventh Chords. Journal of Music Theory. 1998，Vol. 42，No. 2，pp. 182．

[8］COHN R Neo-Riemanninan Operations，Parsimonious Trichords，and Their Tonnetz Representations［J］. Journal of Music Theory. 1997， 41（1）：1-66.

[9］COHN R Weitzmanns Regions，My Cycles，and Douthetts Dancing Cubes［J］. Music Theory Spectrum，2000，22（1）：90.

[10］COHN R，Maximally Smooth Cycles，Hexatonic Systems，and the Analysis of Late-Romantic Triadic Progressions［J］. Music Analysis ，1996，15（1）：10.）

（責任編輯：王肖茜）