一種改進(jìn)的鯨魚優(yōu)化算法在工程上的應(yīng)用

摘要：針對(duì)鯨魚優(yōu)化算法存在收斂速度慢、易于陷入局部最優(yōu)、收斂精度不高等問題，提出一種混合策略的改進(jìn) 鯨魚優(yōu)化算法（LWWOA）.首先在全局搜索階段引入萊維飛行，然后在螺旋更新階段加入一個(gè)隨機(jī)調(diào)整的慣性 權(quán)重，最后將改進(jìn)的鯨魚優(yōu)化算法應(yīng)用于實(shí)際工程的優(yōu)化設(shè)計(jì)問題，應(yīng)用場(chǎng)景包括三桿桁架設(shè)計(jì)和壓力彈簧的 設(shè)計(jì).仿真結(jié)果表明，LWWOA具有較快的收斂速度和較優(yōu)的收斂精度，對(duì)實(shí)際工程的設(shè)計(jì)具有指導(dǎo)意義，并 能拓展到其他領(lǐng)域.

關(guān)鍵詞：鯨魚優(yōu)化算法；萊維飛行；慣性權(quán)重策略；三桿桁架；壓力彈簧

中圖分類號(hào)：TP391.4

文獻(xiàn)標(biāo)志碼：A

Application of an Improved Whale Optimization Algorithm in Engineering

LIN Heng-qing

（College of Mechanical and Intelligent Manufacturing，

Fujian Chuanzheng Communications College， Fuzhou 350007， China）

Abstract： The Whale Optimization Algorithm is a newly proposed population intelligence algorithm in recent years， which has problems such as slow convergence speed， easy to fall into local optima， and low convergence accuracy. In response to the above issues， this article proposes a hybrid strategy based improved whale optimization algorithm （LWWOA）， which first introduces Levy flight in the global search phase， and then adds a randomly adjusted inertia weight in the spiral update phase， at last， applies the improved whale optimization algorithm to practical engineering optimization design problems， including the design of three bar trusses and the design of pressure springs. The simulation results show that LWWOA has a fast convergence speed and excellent convergence accuracy， which has guiding significance for practical engineering design and can be extended to other fields.

Key words： Whale Optimization Algorithm; Levy Flight; inertia weight strategy; three bar truss; compression spring

0引言

群智能優(yōu)化算法作為人工智能最為熱門的研 究?jī)?nèi)容之一，已經(jīng)在學(xué)術(shù)界、工業(yè)界得到了廣泛的 應(yīng)用和實(shí)踐.過去的幾十年，受到自然現(xiàn)象的啟發(fā)，研究者們提出了各種群智能優(yōu)化算法，如黏菌 算法[1]（Slime Moudl algorithm，SMA）、人工蜂 群算法[2]（Artificial Bee Colony Algorithm， ABC）和蝗蟲優(yōu)化算法[3]（Grasshopper Optimisa- tion Algorithm，GOA），還有基于數(shù)學(xué)函數(shù)的黃金正弦算法[4]（Golden Sine Algorithm，GSA）等， 為解決復(fù)雜的優(yōu)化問題提供了強(qiáng)有力支持.

鯨魚優(yōu)化算法（WOA）是一種全新的元啟發(fā)式優(yōu)化算法，它是由Seyedali Mirjalili等[]受到 座頭鯨狩獵行為的啟發(fā)于2016年提出的.該算法模擬鯨魚尋找獵物、包圍獵物和氣泡網(wǎng)攻擊獵物 等捕食行為而達(dá)到優(yōu)化搜索的目的[6].

1標(biāo)準(zhǔn)鯨魚算法

1.1包圍捕獵方式

在狩獵過程中鯨魚能夠識(shí)別獵物的位置并將 其包圍.由于最優(yōu)設(shè)計(jì)在搜索中的位置不是先驗(yàn) 已知的，因此WOA算法假定當(dāng)前最優(yōu)鯨魚個(gè)體 的位置是目標(biāo)獵物位置或接近最優(yōu)解.在定義了 最佳搜索代理（鯨魚）之后，其他搜索代理（鯨魚） 將嘗試向最優(yōu)鯨魚位置靠近包圍來更新它們的位 置，這一行為可表示為：

其中，0.05≤x1≤2；0.25≤x2≤1.3；2≤x3≤15.

4實(shí)驗(yàn)結(jié)果與分析

4.1實(shí)驗(yàn)環(huán)境

本文的仿真實(shí)驗(yàn)環(huán)境為：Windows10操作系統(tǒng)；Intel（R）Core（TM）I5處理器3.2GHz、8GB內(nèi)存；GTX1050顯卡，軟件環(huán)境使用Python 語言編程開發(fā).

4.2數(shù)據(jù)預(yù)處理

本文將所提出的改進(jìn)算法LWWOA與人工 蜂群算法（ABC）、蝗蟲優(yōu)化算法（GOA）和黏菌算法（SMA）進(jìn)行測(cè)試對(duì)比.為了能夠客觀反映實(shí)驗(yàn) 結(jié)果，統(tǒng)一設(shè)置各算法種群數(shù)量為30，最大迭代 次數(shù)設(shè)為100，每種算法在兩個(gè)場(chǎng)景中分別進(jìn)行 30次獨(dú)立實(shí)驗(yàn).

場(chǎng)景1下的實(shí)驗(yàn)結(jié)果如圖3所示.LW-WOA、SMA、GOA、ABC算法分別對(duì)應(yīng)不同線 形.從圖中可以看出，幾種算法的適應(yīng)度函數(shù)值不 斷減小，最終輸出了一組滿足約束條件的參數(shù)，幾 種算法的最終輸出值相差不大，相比之下LW-WOA算法得出的值最小，更加接近最優(yōu)解.雖然 在開始搜索階段LWWOA的初始值比其他算法更遠(yuǎn)離最優(yōu)值，但是它收斂速度最快，經(jīng)過20次 左右的迭代收斂到極值.

場(chǎng)景1的30次實(shí)驗(yàn)對(duì)比結(jié)果如表1所列，表 中列舉了30次實(shí)驗(yàn)的最小值、最大值、平均值及 標(biāo)準(zhǔn)差，用以分析算法的優(yōu)劣.從表1中看出，在場(chǎng)景1中LWWOA無論是在尋優(yōu)精度還是算法 穩(wěn)定性方面相比其他3種智能算法表現(xiàn)更好.

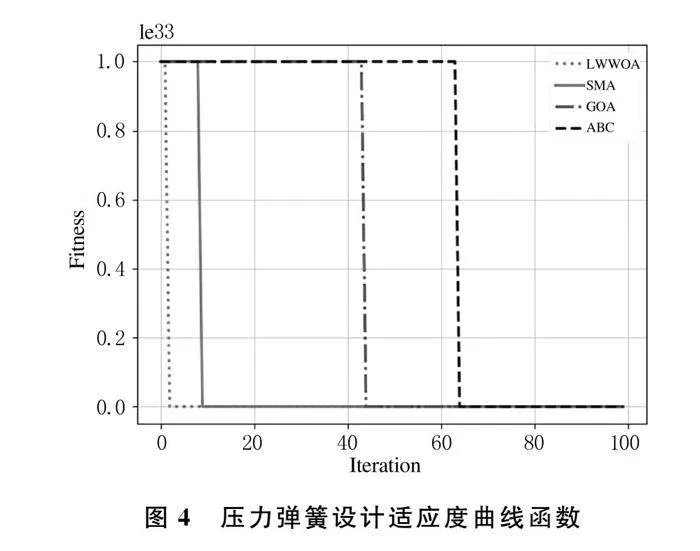
場(chǎng)景2下的實(shí)驗(yàn)結(jié)果如圖4所示.從圖中可 以看出，幾種算法的適應(yīng)度函數(shù)值迅速下降，收斂 曲線的斜率近乎垂直，最終輸出了一組滿足約束 條件的參數(shù).通過對(duì)比幾種算法的最終適應(yīng)度值 幾乎相同，但是在收斂速度上LWWOA算法更 勝一籌.

從以上兩個(gè)實(shí)際工程的應(yīng)用可以看出，與其 他智能優(yōu)化算法相比，結(jié)合了Levy Flight和隨機(jī) 調(diào)整的慣性權(quán)重的鯨魚算法尋優(yōu)性能更佳，在全 局搜索階段引入Levy Flight進(jìn)行優(yōu)化，提升了全 局搜索能力，加快了收斂速度[10].在局部搜索階 段引入隨機(jī)調(diào)整慣性權(quán)重，由于較大和較小權(quán)重 都隨機(jī)出現(xiàn)，有利于局部和全局搜索的平衡，更容 易找到最優(yōu)解.

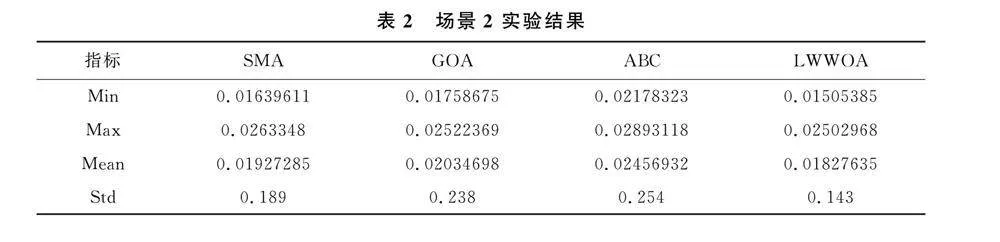
場(chǎng)景2的30次實(shí)驗(yàn)結(jié)果對(duì)比情況如表2所 列，表中列舉了30次實(shí)驗(yàn)的最小值、最大值、平 均值及標(biāo)準(zhǔn)差用以分析算法的優(yōu)劣.從表2中看出，在場(chǎng)景2中LWWOA無論是在尋優(yōu)的精度 還是算法的穩(wěn)定性方面要優(yōu)于其他3種智能算 法.

5結(jié)語

鯨魚優(yōu)化算法是一種基于自然界中鯨魚群體 行為的優(yōu)化算法，標(biāo)準(zhǔn)鯨魚算法存在諸如收斂速 度慢、易于陷入局部最優(yōu)、收斂精度不高等一些問 題，本文提出了具有萊維飛行和隨機(jī)調(diào)整的慣性 權(quán)重策略融合的鯨魚優(yōu)化算法（LWWOA）.經(jīng)過仿真實(shí)驗(yàn)可以看出，LWWOA可以應(yīng)用于實(shí)際工 作中的優(yōu)化設(shè)計(jì)，算法性能優(yōu)于其他幾種算法，有 助于提高工程項(xiàng)目的效率和性能.LWWOA具有 很大的應(yīng)用前景，可以進(jìn)一步拓展到更多的領(lǐng)域.

參考文獻(xiàn)：

[1] LI S M，CHEN H L，WANG M J，et al. Slime mould algorithem：a new method for stochastic optimization [J]. Future Generation Computer Sysetems， 2020，111：300-323.

[2] KARABOGA D， BASTURK B. A powerful and efficient algorithm for numerical function optimization： artificial bee colony （ABC） algorithm [J]. Journal of

Global Optimization，2007，39（3）：459-471.

[3] SAREMI S， MIRJALILI S， LEWIS A. Grashopper optimisaton algoritm： theory and application[J]. Advances in Engineering Software，2017，105：33-47.

[4] TANYILDIZI E， DEMIR G. Golden sine algoritm： a novel math-ispired algorithm[J]. Advances Electrial amp;. Computer Engineering，2017，17（2）：71-78.

[5] SEYEDALI M，ANDREW L. The whale optimization algorithm [J]. Advances in Engineering Software，2016，95：51-67.

[6]李鑫.改進(jìn)的鯨魚優(yōu)化算法研究[D].阜新：遼寧工程 技術(shù)大學(xué)，2021.

[7]徐航，張達(dá)敏，王依柔，等.混合策略改進(jìn)鯨魚優(yōu)化算 法[J].計(jì)算機(jī)工程與設(shè)計(jì)，2020，41（12）：3397-3404.

[8]周歡.基于改進(jìn)布谷鳥算法的電子商務(wù)配送中心選址研究[D].鄭州：河南大學(xué)，2016.

[9]汪逸暉，高亮.烏鴉搜索算法的改進(jìn)及其在工程約束 優(yōu)化問題中的應(yīng)用[J].計(jì)算機(jī)集成制造系統(tǒng)，2021（7）：1871-1883.

[10]李建偉，于廣濱.改進(jìn)麻雀搜索算法的輪轂減速器優(yōu) 化設(shè)計(jì)[J].哈爾濱理工大學(xué)學(xué)報(bào)，2022（5）：56-63.

[責(zé)任編輯：李嵐]