電連接器用聚氨酯膠密封件貯存可靠性統(tǒng)計模型的加速試驗驗證與評估

錢萍 陳馳 陳文華 吳山奇 郭明達

摘要：

針對電連接器用聚氨酯膠密封件在長貯條件下的壽命評估問題，從機理層面分析了聚氨酯膠密封件內(nèi)聚破壞和邊界破壞導致性能下降的原因。依據(jù)從機理層面建立的電連接器用聚氨酯膠密封件貯存可靠性統(tǒng)計模型，利用聚氨酯膠密封件溫濕度綜合應力加速退化試驗數(shù)據(jù)，綜合應用粒子群優(yōu)化算法和回歸分析、AD檢驗及擬合優(yōu)度等檢驗方法，從數(shù)據(jù)統(tǒng)計層面驗證了電連接器用聚氨酯膠密封件失效物理方程和退化軌跡模型的合理性。利用掃描電鏡和能譜分析驗證了失效機理分析的正確性。最后，利用所建模型評估了電連接器用聚氨酯膠密封件在貯存環(huán)境下的可靠壽命。

關(guān)鍵詞：電連接器；密封失效機理；加速試驗；統(tǒng)計檢驗；可靠性評估

中圖分類號：V442；TB114

DOI：10.3969/j.issn.1004132X.2024.05.014

開放科學（資源服務(wù)）標識碼（OSID）：

Accelerated Test Verification and Evaluation of Storage Reliability Statistical

Model of Polyurethane Sealing Elements for Electrical Connectors

QIAN Ping? CHEN Chi? CHEN Wenhua? WU Shanqi? GUO Mingda

Zhejiang Provinces Key Laboratory of Reliability Technology for Mechanical and Electrical Product，

Zhejiang Sci-Tech University，Hangzhou，310018

Abstract： In order to address the issues of life evaluation for polyurethane sealing elements used in electrical connectors during prolonged storage conditions， the underlying mechanism behind cohesion failure and boundary failure that contributed to performance degradation of these seals was analyzed. The reliability statistical model of polyurethane sealing elements for electrical connectors， established at the mechanism level， was validated at a statistical level by comprehensively applying particle swarm optimization algorithm and regression analysis， AD test and goodness of fit test methods to the comprehensive stress accelerated degradation data of temperature and humidity on polyurethane sealing elements. The validity of the failure mechanism analysis was confirmed through SEM and EDS techniques. Ultimately， the developed model was employed to assess the reliable lifespan of polyurethane adhesive seals for electrical connectors under the? storage environment.

Key words： electrical connector; seal failure mechanism; accelerated test; statistical test; reliability evaluation

收稿日期：20231230

基金項目：浙江省重點研發(fā)計劃（2021C01133）

0? 引言

長期貯存、一次使用的型號裝備在服役后絕大部分時間處于貯存狀態(tài)，電連接器作為一種基礎(chǔ)機電元件，是型號裝備的電氣系統(tǒng)中傳遞電能和信號必不可少的關(guān)鍵元器件，其貯存可靠性對型號系統(tǒng)的壽命影響很大。

目前對電連接器貯存可靠性的研究主要集中在接觸性能［1-3］和絕緣性能［4-6］。密封件作為電連接器中的核心組件之一，其主要功能是保護電連接器的內(nèi)部結(jié)構(gòu)，實現(xiàn)電連接器內(nèi)外空間的隔離。密封件在貯存環(huán)境的長期作用下，其性能會逐漸下降，從而影響接觸性能和絕緣性能，造成內(nèi)部電路的損壞［7］。

目前國內(nèi)外對密封件模型的研究主要集中在工作環(huán)境下性能變化的模型研究［8-9］和設(shè)計參數(shù)對密封性能影響的模型研究［10-11］，通過以上模型可以很好地反映密封件在工作環(huán)境下的性能變化情況，為密封件的設(shè)計提供參考。對于貯存狀態(tài)下密封件的可靠性模型，目前已有的研究報道尚少，主要為基于數(shù)據(jù)的可靠性模型［12-13］研究以及少量的機理層面模型［14］研究，然而上述研究所采用的模型是否能確切描述密封件性能在貯存環(huán)境下的演變規(guī)律，并未經(jīng)過嚴格驗證，模型的偏差將導致密封件可靠性評估產(chǎn)生較大誤差，因此有必要通過實施加速試驗，從統(tǒng)計角度對失效機理層面建立的密封件可靠性統(tǒng)計模型進行驗證，以獲得較高的估計精度。

目前，對可靠性模型的驗證主要從退化量分布檢驗［15］、退化軌跡模型檢驗［16］和失效物理方程檢驗［17］等角度展開，并根據(jù)模型的種類選擇合適的角度進行模型驗證。本文所驗證的可靠性模型為基于失效機理的貯存環(huán)境應力下密封件的可靠性模型，包含退化量分布、退化軌跡模型以及失效物理方程三個方面的內(nèi)容，因此有必要從上述三個角度對模型進行驗證，以保證模型的正確性。

本文以電連接器常用的聚氨酯膠密封件為對象，基于失效機理層面建立的性能退化模型和加速模型，通過實施溫濕度綜合應力加速試驗，利用試驗數(shù)據(jù)和統(tǒng)計檢驗方法對所建模型的合理性和正確性進行驗證；進一步地，基于檢驗后的模型評估電連接器用聚氨酯膠密封件在實際貯存環(huán)境下的可靠壽命。

1? 電連接器用聚氨酯膠密封件在溫濕度綜合應力作用下的可靠性統(tǒng)計模型

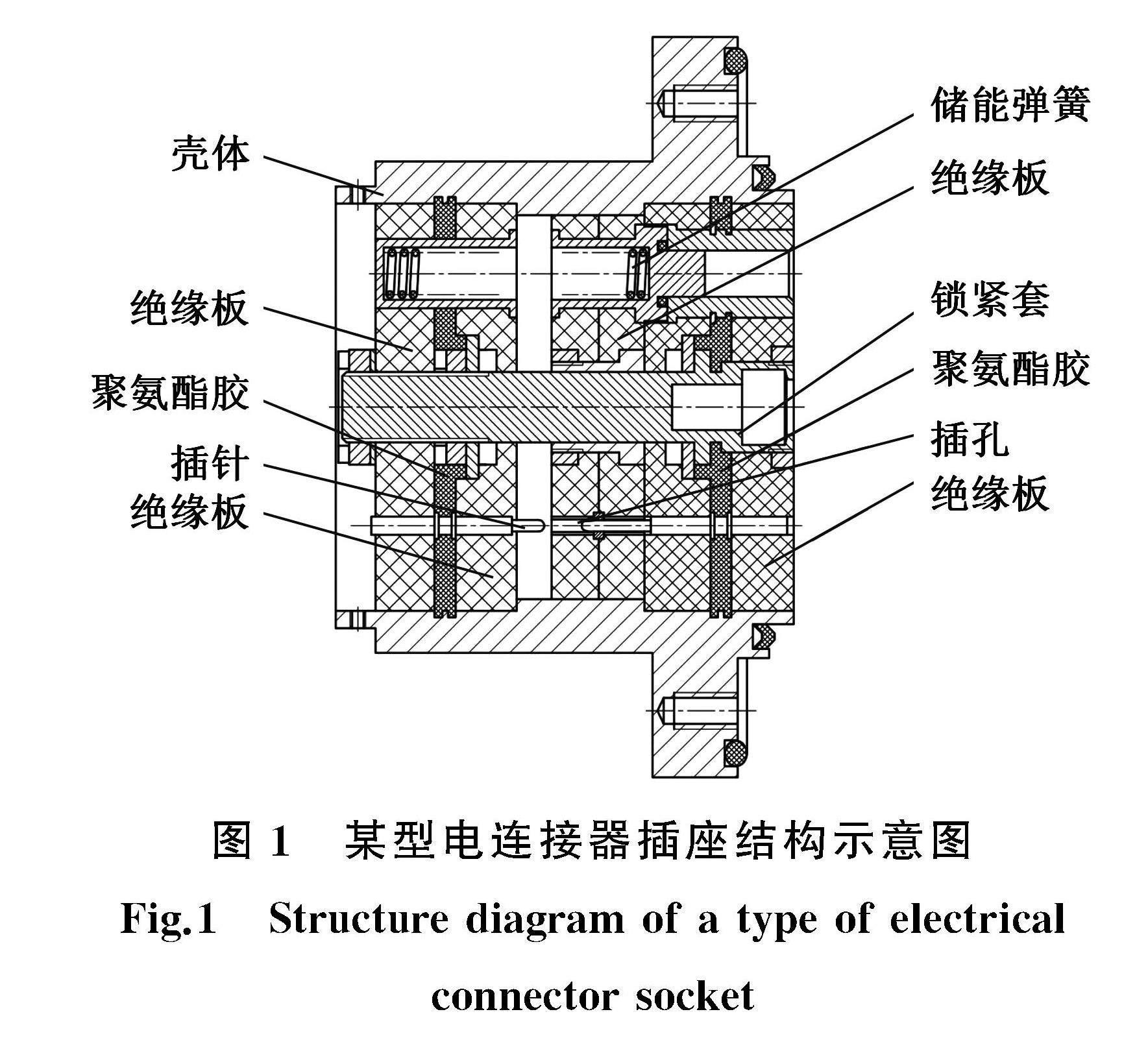
電連接器用聚氨酯膠密封件是一種通過混合JA-2S和MOCA固化劑并在制膠工藝后注入電連接器中形成的一層密封層，通常灌裝在兩層絕緣板之間，如圖1所示，能夠?qū)崿F(xiàn)電連接器內(nèi)外空間的隔離，阻止有害物質(zhì)進入到電連接器內(nèi)部，避免由于密封問題導致的電連接器失效。

1.1? 失效機理

聚氨酯膠密封件中含有大量的醚基、氨基甲酸酯和脲基基團［18］，在溫度和濕度應力的綜合作用下，電連接器用聚氨酯膠密封件會發(fā)生氧化和水解反應［19-20］，主要表現(xiàn)為醚基與空氣中氧氣的氧化反應以及氨基甲酸酯和脲基與空氣中水分的水解反應，導致聚氨酯膠中醚基、氨基甲酸酯和脲基基團化學鍵斷裂，造成聚氨酯膠密封件致密度下降和邊界吸附能力降低，從而導致電連接器用聚氨酯膠密封件發(fā)生內(nèi)聚破壞和邊界破壞［21-22］，造成密封性能的下降。

在貯存環(huán)境下，電連接器用聚氨酯膠密封件受到溫度和濕度的共同作用而發(fā)生氧化和水解并且兩個反應過程相互促進。溫度升高不僅加快氧化速率，還使得水解反應分子的活性增強，從而促進水解反應過程的進行；濕度提高，水解反應速率加快，更易引起致密度下降，導致內(nèi)部孔隙產(chǎn)生，使得氧氣更容易接觸到聚氨酯膠內(nèi)部，促進氧化反應的進行。

隨著時間的推移，在氧化和水解反應的共同作用下，密封件的致密度和分子吸附能力逐漸下降，內(nèi)聚破壞和邊界破壞的程度逐漸加劇，加速了聚氨酯膠密封件的老化過程，導致密封件的密封性能越來越差。

1.2? 失效物理方程

貯存環(huán)境下，聚氨酯膠密封件中的醚基與空氣中的氧氣發(fā)生反應，其化學反應式為

（CH2）4O（CH2）4+O2→（CH2）3COOH（CH2）4OH

該反應導致醚基發(fā)生斷鍵造成孔洞數(shù)量增加，醚基消耗越多，密封性能下降越明顯。根據(jù)質(zhì)量作用定律［23］，由醚基氧化導致的表征密封件內(nèi)部孔洞變化的性能退化參數(shù)GT可表示為

GT=Aexp（－EaKBT）C（CH2）4O（CH2）4CO2t（1）

式中，A為活化分子碰撞數(shù)；Ea為活化能，eV；KB為玻爾茲曼常數(shù)，J/K;T為絕對溫度，K；C（CH2）4O（CH2）4為醚基的濃度；CO2為氧氣的濃度；t為時間，h。

在濕度應力下，聚氨酯膠中的氨基甲酯和脲基會同時與空氣中的水發(fā)生反應，其化學反應方程式分別為

RNHCOOR+H2O→RNHCOOH+ROH

RNHCONHR+H2O→RNHCOOH+H2NR

以上反應將導致聚氨酯膠中的氨基甲酯和脲基發(fā)生降解斷鍵，造成孔洞數(shù)量增加，引起密封性能下降，氨基甲酯和脲基降解越多，密封性能下降越明顯。根據(jù)質(zhì)量作用定律，由氨基甲酯和脲基水解導致的表征密封件內(nèi)部孔洞變化的性能退化參數(shù)GRH可表示為

GRH=k1k2CRNHCOORCRNHCONHRC2RHt（2）

式中，k1為氨基甲酯的水解速率常數(shù)；k2為脲基的水解速率常數(shù)；CRH為環(huán)境濕度；CRNHCOOR為氨基甲酯的濃度；CRNHCONHR為脲基的濃度。

在貯存環(huán)境溫濕度的作用下，聚氨酯膠的氧化和水解反應同時進行且相互促進，令G表征由氧化和水解反應共同引起的密封件內(nèi)部孔洞變化的性能退化參數(shù)，由式（1）和式（2）可知，它與溫濕度之間的關(guān)系可表示為［14］

G=GTGRH=Z1C2RHexp（－EaKBT）t2（3）

Z1=Ak1k2C（CH2）4O（CH2）4CO2CRNHCOORCRNHCONHR

1.3? 退化軌跡模型

聚氨酯膠密封件的內(nèi)聚破壞主要是由于聚氨酯膠材料的氧化水解造成聚氨酯膠密封件內(nèi)部孔隙數(shù)目增加以及孔隙尺寸增大。由內(nèi)聚破壞引起的氣體泄漏率主要與內(nèi)外兩側(cè)壓強差Δp、橫截面積S以及聚氨酯膠密封件的厚度w有關(guān)，其表達式［14］為

Q1=Gγp-SΔp4ηw（4）

式中，Q1為由內(nèi)聚破壞導致的氣體泄漏率，Pa·m3/s；γ為氣體擴散隨機系數(shù)，γ～N（μγ，σγ），μγ、σγ分別為γ的均值和標準差；p-為孔隙內(nèi)平均壓力，Pa；η為氣體黏度，Pa·s。

邊界破壞主要是由于聚氨酯膠表面吸附能力降低造成聚氨酯膠與接觸件和殼體粘接界面的粘接力減小。根據(jù)Roth密封理論［24］，密封件的邊界破壞引起的氣體泄漏率主要與氣體溫度T0、單個氣體分子質(zhì)量m0、接觸面粗糙度H、接觸周長L、密封件厚度w、表面密封系數(shù)RS、內(nèi)外兩側(cè)壓強差Δp以及作用在密封件表面的應力σn有關(guān)，其表達式［14］為

Q2=8KBT0πm0H2LwΔpexp（－3σnRS）（5）

式中，Q2為由邊界破壞導致的氣體泄漏率，Pa·m3/s；L～N（μL，σL），μL、σL分別為L的均值和標準差。

根據(jù)Morse吸附理論［25］和Maxwell模型［26］，可確定密封件表面的應力σn為

σn=Z3（exp（2Z2G）－exp（Z2G））+σ0exp（－tE0χ）（6）

式中，Z2、Z3為待估參數(shù)；σ0為密封件灌裝在絕緣板之間的初始彈性應力，MPa；E0為聚氨酯膠的彈性模量，MPa；χ為聚氨酯膠的黏度系數(shù)，Pa·s。

電連接器用聚氨酯膠密封件的泄漏率由內(nèi)聚破壞泄漏率和邊界破壞泄漏率組成，依據(jù)未知內(nèi)聚破壞和邊界破壞的所占比例，引入比例系數(shù)Z4、Z5，則電連接器用聚氨酯膠密封件的泄漏率退化軌跡模型為

Qt=Q0+Z4Gγp-SΔp4ηw+

Z58KBT0πm0H2LwΔpexp（－3σnRS）（7）

式中，Q0為聚氨酯膠密封件氣體泄漏率初值，Pa·m3/s；Qt為在t時刻下聚氨酯膠密封件氣體泄漏率，Pa·m3/s。

1.4? 可靠性統(tǒng)計模型

在長期貯存過程中，電連接器聚氨酯膠密封件的性能會逐漸退化，其氣體泄漏率值將逐漸增大。當泄漏率達到失效閾值QD時電連接器會發(fā)生密封失效，此時對應的壽命te的數(shù)學表達式如下：

te=inf{t：Qt>QD}（8）

由于氣體擴散隨機系數(shù)γ和接觸周長L服從正態(tài)分布，故t時刻下聚氨酯膠密封件的氣體泄漏率Qt服從正態(tài)分布，分布函數(shù)為

FQt（X）=∫X012πσQtexp（－（Qt－μQt）22σ2Qt）dQt（9）

式中，X為隨機變量；FQt（X）表示Qt≤X的概率；μQt為Qt的均值；σQt為Qt的標準差。

在貯存時間t時刻下，電連接器用聚氨酯膠密封件的可靠度函數(shù)為

R（t）=P（Qt≤QD）=

∫QD012πσQtexp（－（Qt－μQt）22σ2Qt）dQt（10）

2? 溫濕度綜合應力加速試驗方案的確定

2.1? 試驗應力水平和截尾時間

根據(jù)聚氨酯膠材質(zhì)特性，聚氨酯膠密封件的最高耐受溫度為85 ℃，為保證聚氨酯膠密封件在加速試驗過程中的失效機理不變，將試驗的最高溫度應力水平設(shè)定為75 ℃，同時為保證試驗具有一定的加速性，其余溫度設(shè)置為55 ℃和65 ℃。結(jié)合試驗設(shè)備的可行域，本文將濕度應力設(shè)置為96%RH、84%RH 和72%RH 。根據(jù)國家標準GB/T 2689.1—1981中的有關(guān)要求［27］，為保證試驗評估精度，每個應力水平下投放12個樣品。

考慮到統(tǒng)計精度和模型驗證的要求，基于中心復合設(shè)計法可以挖掘出因素與響應值之間的關(guān)系并且具有延順性的特點［28］，選取其中5組溫濕度應力水平組合開展試驗。由于聚氨酯膠密封件在不同應力水平組合下的退化速率不同，為了獲取盡可能多的試驗數(shù)據(jù)，確定（55 ℃，72%RH）、（65 ℃，96%RH）、（65 ℃，84%RH）水平組截尾時間為1500 h，（75 ℃，96%RH）、（75 ℃，72%RH）水平組截尾時間為1000 h，測試間隔均為336 h。具體試驗方案如表1所示。

2.2? 失效判據(jù)及試樣制備

為保證試驗樣品能夠真實反映聚氨酯膠密封件在電連接器中的實際狀態(tài)，同時考慮到節(jié)約人力和物料資源，制備圖2所示的試驗樣品，其中密封件材料為聚氨酯膠，上下用絕緣板固定，絕緣板中間安裝10根插針。

根據(jù)聚氨酯膠密封件性能退化模型，確定試驗測試參數(shù)為氣體泄漏率，測試時按GJB1217—1991［29］規(guī)范進行測試，測試儀器為VSBR152型號氦氣質(zhì)譜檢漏儀，其主要技術(shù)指標如表2所示。

依據(jù)GJB 142—1986［30］，確定電連接器用聚氨酯膠密封件的氣體泄漏率失效閾值為1×10－6 Pa·m3/s。

3? 加速試驗數(shù)據(jù)統(tǒng)計分析與模型驗證

按照表1所示的試驗方案，對聚氨酯膠密封件實施5組溫濕度綜合應力下的加速退化試驗，

截止到規(guī)定的試驗時間，所有樣品均未發(fā)生密封失效，各組試驗應力水平下聚氨酯膠密封件的退化軌跡如圖3所示。

3.1? 模型參數(shù)估計

根據(jù)聚氨酯膠密封件的材料、結(jié)構(gòu)和加速試驗的相關(guān)參數(shù)，可確定退化模型中的部分參數(shù)值如表3所示，模型中的隨機參數(shù)Z1、Z2、Z3，比例系數(shù)Z4、Z5，接觸周長的均值μL和標準差σL，擴散系數(shù)的均值μγ和標準差σγ，初始彈性應力σ0，黏度系數(shù)χ，密封性能參數(shù)RS以及活化能Ea為待估參數(shù)。

基于粒子群算法精度高、優(yōu)化速度快等優(yōu)點［31］，此處采用粒子群算法對模型參數(shù)進行估計。首先，建立一個適應度函數(shù)為

Ffit=∑Ni=1（yi－y^i）2N（11）

式中，yi（i=1，2，…，N）為樣品在第i次測試時的實測值均值；y^i為樣品在第i次測試時的氣體泄漏率擬合值；N為樣品測試次數(shù)。

將試驗數(shù)據(jù)和模型代入下式所示的粒子群算法中［32］進行運算：

v（m+1）kd=v（m）kd+c1Vrand（pkd－x（m）kd）+

c2Vrand（pgk－x（m）kd）

x（m+1）kd=x（m）kd+v（m+1）kd（12）

式中，x（m）kd為第m次迭代后參數(shù)k粒子群中粒子d的估計結(jié)果；v（m）kd為第m次迭代時參數(shù)k粒子群中粒子d的數(shù)值變化量；c1、c2為加速因子；Vrand為0～1之間的隨機數(shù)； pkd為參數(shù)k粒子群中粒子d搜索到的最優(yōu)值； pgk為參數(shù)k粒子群中所有粒子搜索到的最優(yōu)值。

求得待估參數(shù)后，分別單獨對每個樣品進行參數(shù)估計并得到對應的L和γ值，根據(jù)下式即可得到接觸周長和擴散系數(shù)的標準差σL和σγ：

σ2=1n∑nr=1（xr－μ）2（13）

式中，n為樣品的數(shù)量；xr為第r個樣品的參數(shù)估計值;μ為參數(shù)估計值的均值。

經(jīng)過多輪迭代即可估算出所需未知參數(shù)的值，如表4所示。

3.2? 失效物理方程的驗證

失效物理方程的驗證，即驗證該方程能否準確描述產(chǎn)品性能退化參數(shù)在試驗應力下的變化規(guī)律。為了驗證表征電連接器用聚氨酯膠密封件性能退化參數(shù)G與溫濕度之間的數(shù)學關(guān)系失效物理方程（式（3））的合理性，對式（3）兩邊取對數(shù)，令z=ln G，x=1/T，y=ln CRH，可將式（3）轉(zhuǎn)換為z關(guān)于x和y的線性方程。在三維空間內(nèi)，若不同應力水平下的三維空間點（x，y，z）在一個平面內(nèi)則可證明式（3）成立，否則不成立。采用回歸分析法對5組應力水平組合下的各點（xj，yj）（j=1，2，3，4，5）對應的zj共面性進行檢驗，建立如下二元線性回歸模型：

zj=γ0+γ1xj+γ2yj（14）

其中，zj=ln Gj，可根據(jù)某一時刻下的氣體泄漏率和式（7）所示的退化軌跡模型確定；xj=1/Tj；yj=ln CRHj；γ0、γ1、γ2為回歸模型的待估參數(shù)。

取5組應力水平的共同測試點t=1008 h，利用此時刻下的氣體泄漏率數(shù)據(jù)點代入式（7）可計算出對應的zj；利用最小二乘法對參數(shù)γ0、γ1、γ2進行估計，得到對應的估計值依次為γ^0=－6.48，γ^1=－18 916，γ^2=2。

三維空間點（xj，yj，zj）和擬合平面z^j=γ^0+γ^1xj+γ^2yj在三維空間內(nèi)的位置如圖4所示。

為了進一步定量檢驗失效物理方程是否準確，采用基于反映二元線性回歸模型（式（14））和試驗數(shù)據(jù)擬合程度的方差分析法來構(gòu)造檢驗統(tǒng)計量，具體表達式如下［33］：

FH（M，K-M-1）=（VSS-VSSE）/MVSSE/（K-M-1）（15）

VSSE=∑Kj=1（z^j－zj）2（16）

VSS=∑Kj=1（zj－z-）2（17）

z-=1K∑Kj=1zj（18）

式中，VSS為回歸平方和；VSSE為殘差平方和；z^j為對應溫濕度下的回歸模型擬合值，z-為K組zj值的平均值；M為應力的個數(shù)，此處取M=2；K為應力水平的數(shù)目，此處取K=5。

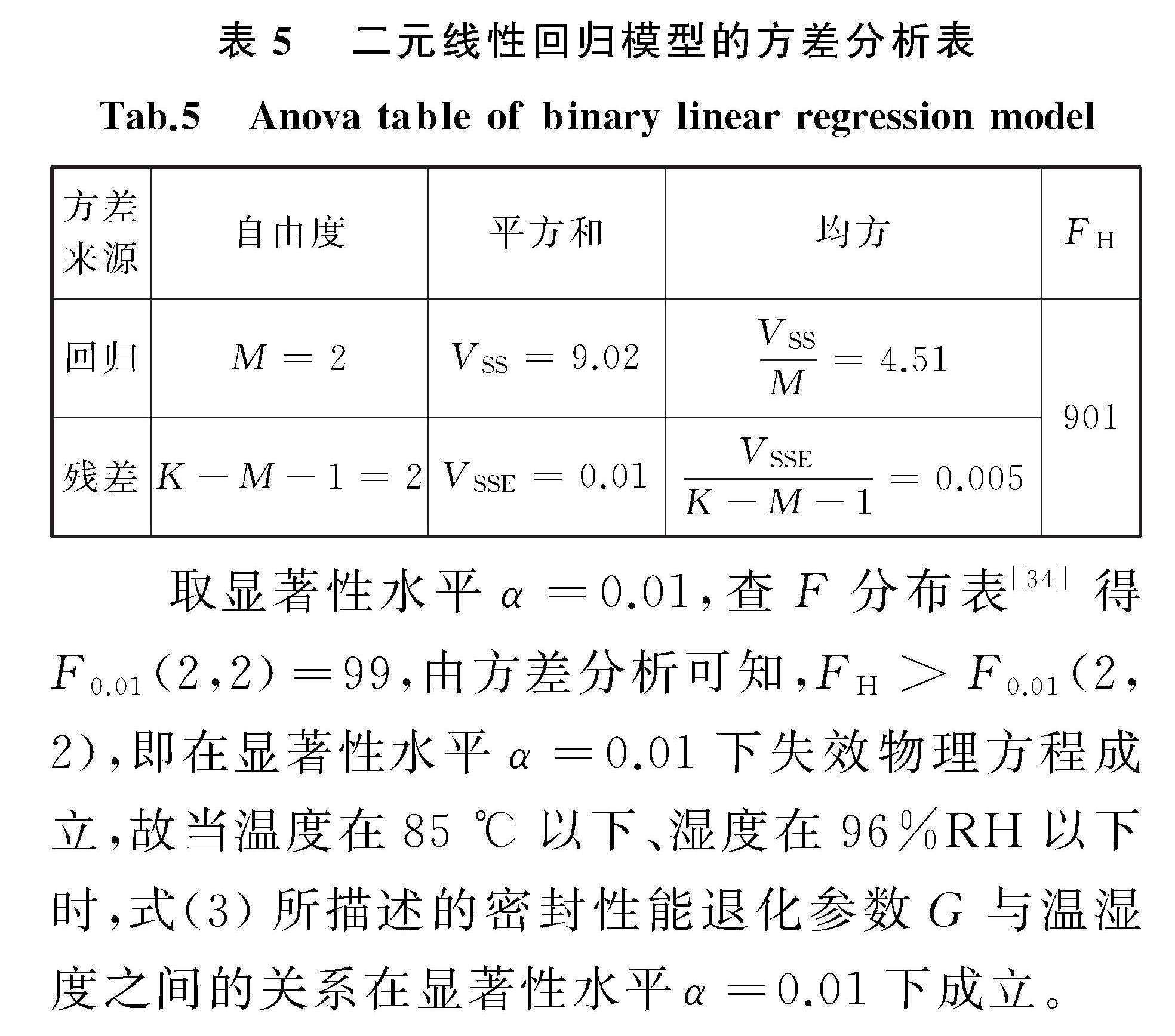
基于式（15）～式（18），二元線性回歸模型的方差分析結(jié)果如表5所示。

取顯著性水平α=0.01，查F分布表［34］得F0.01（2，2）=99，由方差分析可知，F(xiàn)H>F0.01（2，2），即在顯著性水平α=0.01下失效物理方程成立，故當溫度在85 ℃以下、濕度在96%RH以下時，式（3）所描述的密封性能退化參數(shù)G與溫濕度之間的關(guān)系在顯著性水平α=0.01下成立。

3.3? 退化量分布的驗證

為了驗證模型中關(guān)于電連接器用聚氨酯膠密封件的氣體泄漏率服從正態(tài)分布的假設(shè)，采用A-D檢驗法［35］，取顯著性水平α=0.05，若根據(jù)A-D統(tǒng)計量分布計算出的P值大于0.05，則接受氣體泄漏率服從正態(tài)分布的假設(shè)。對5組試驗樣品在不同檢測時間點的氣體泄漏率進行正態(tài)性檢驗，檢驗結(jié)果如表6所示。

從表6中可以看出，5組樣品在各個時刻下退化量的正態(tài)性檢驗結(jié)果P值均大于0.05，可在95%置信度認為聚氨酯膠密封件的氣體泄漏率服從正態(tài)分布，驗證了所建模型中退化量服從正態(tài)分布假設(shè)的正確性。

3.4? ?退化軌跡模型的驗證

由于電連接器用聚氨酯膠密封件性能退化軌跡模型為非線性模型，基于RNL擬合優(yōu)度的靈敏度和分辨率較高且可以用于檢驗非線性軌跡模型［36］，故此處采用RNL表示曲線模型的擬合優(yōu)度，則RNL的表達式為

RNL=1－∑Ni=1（yi－y^i）2∑Ni=1y2i（19）

其中，RNL的取值范圍為（0，1），該值越接近于1，表明模型的擬合程度越高，5組試驗的擬合優(yōu)度RNL計算結(jié)果如表7所示。

由表7可知，5組試驗的RNL計算結(jié)果均大于0.95，表明電連接器用聚氨酯膠密封件的退化軌跡模型能較好地擬合試驗數(shù)據(jù)，驗證了聚氨酯膠密封件退化軌跡模型的正確性，從而驗證了所建的聚氨酯膠密封件貯存可靠性模型的合理性。

3.5? 貯存可靠壽命估計

基于驗證后的電連接器用聚氨酯膠密封件的性能退化軌跡模型、失效物理方程和可靠性統(tǒng)計模型，利用最小二乘估計和極大似然估計法計算得到25 ℃、50%RH貯存環(huán)境下密封件的可靠壽命，如表8所示。

4? 失效機理驗證

為了驗證電連接器用聚氨酯膠密封件在貯存狀態(tài)下失效機理分析的正確性，利用掃描電子顯微鏡對試驗后的聚氨酯膠密封件的形貌進行掃描，結(jié)果如圖5所示，可以看出聚氨酯膠內(nèi)部產(chǎn)生了孔洞和塌陷，可認為內(nèi)聚破壞是密封性能下降的主要原因之一。

通過對聚氨酯膠密封件與鋁合金殼體、接觸件接觸處的粘接面進行能譜分析，如圖6所示，發(fā)現(xiàn)在粘接面處未出現(xiàn)鋁元素和金元素，故可認為聚氨酯膠未與鋁和金發(fā)生反應產(chǎn)生化學鍵連接，其連接主要依靠聚氨酯膠的物理吸附力和彈性力。根據(jù)極性相似原則［37］，吸附力由聚氨酯膠中的分子基團提供，故可判定密封件發(fā)生邊界破壞是由分子基團氧化水解引起的，從而驗證了失效機理分析的正確性。

5? 結(jié)論

本文利用加速退化試驗對從失效機理層面建立的電連接器用聚氨酯膠密封件失效物理方程、密封性能退化軌跡模型和可靠性統(tǒng)計分布模型進行了驗證，并評估了聚氨酯膠密封件在貯存環(huán)境下的可靠壽命，主要結(jié)論如下：

（1）通過開展5組溫濕度綜合應力下加速試驗，獲得了聚氨酯膠密封件在不同溫濕度應力下的性能退化數(shù)據(jù)，利用粒子群算法對模型參數(shù)進行估計，聯(lián)合回歸分析法、AD檢驗法和RNL擬合優(yōu)度等統(tǒng)計檢驗法驗證了所建模型的正確性，給出了實際貯存環(huán)境下電連接器用聚氨酯膠密封件的貯存可靠壽命。

（2）對試驗后的樣品進行電鏡掃描和能譜分析，驗證了電連接器用聚氨酯膠密封件的失效機理分析的正確性。

參考文獻：

［1］? 林敏. 收口量與鍍金層厚度對接觸件貯存壽命影響規(guī)律的研究［D］. 杭州：浙江理工大學， 2023.

LIN Min. Study on the Influence of Closing Quantity and Plating Thickness on the Storage Life of Contact Parts［D］. Hangzhou：Zhejiang Sci-tech University， 2023.

［2］? 梁淑雅. 簧絲傾角對電連接器接觸件可靠性影響規(guī)律的研究［D］. 杭州：浙江理工大學， 2022.

LIANG Shuya. Research on the Effects of Wire-Spring Angle on the Reliability of Electrical Connector Contacts［D］. Hangzhou：Zhejiang Sci-tech University， 2022.

［3］? 劉娟. 電連接器步進應力加速退化試驗技術(shù)的研究［D］. 杭州：浙江大學， 2013.

LIU Juan. Research on Step-stress Accelerated Degradation Test Technology of Electrical Connector［D］. Hangzhou：Zhejiang University， 2013.

［4］? ZHANG Xinxi， LI Kun， XU Jun. The Research of Insulation Failure on Signals Transmission in Electrical Connector［C］∥2011 Second International Conference on Mechanic Automation and Control Engineering. Inner Mongolia：IEEE， 2011：1797-1799.

［5］? 蔣海濤. 環(huán)境溫度及絕緣材料對電連接器絕緣電阻的影響［J］. 電子技術(shù)與軟件工程， 2021（10）：222-223.

JIANG Haitao. Influence of Ambient Temperature and Insulation Materials on Insulation Resistance of Electrical Connectors［J］. Electronic Technology & Software Engineering， 2021（10）：222-223.

［6］? 王友維. 電連接器用G100硅橡膠絕緣件可靠性建模與試驗評估的研究［D］. 杭州：浙江理工大學， 2023.

WANG Youwei. Study on Reliability Modeling and Test Evaluation of G100 Silicone Rubber Insulator for Electrical Connectors［D］. Hangzhou：Zhejiang Sci-tech University， 2023.

［7］? HU Yujing， HU Wei， YANG Wen， et al. The Corrosion Analysis and Prevention of Secondary Cable Joints Used in Outdoor Terminal Boxes of Substation in Humid Environment［C］∥2020 5th International Conference on Renewable Energy and Environmental Protection， ICREEP 2020. Shenzhen：IOP Publishing Ltd.， 2021：1-7.

［8］? 顧志威， 郭飛， 譚桂斌， 等. 基于流固耦合的橡膠O形圈老化對密封性能的影響研究［J］. 潤滑與密封， 2023， 48（7）：21-26.

GU Zhiwei， GUO Fei， TAN Guibin， et al. Research on the Influence of Rubber O-ring Aging on Sealing Performance Based on Fluid-solid Coupling［J］. Lubrication Engineering， 2023，48（7）：21-26.

［9］? 趙勇. 往復運動下泛塞封密封性能仿真分析與試驗研究［D］. 無錫：江南大學， 2023.

ZHAO Yong. Simulation Analysis and Experimental Study of the Spring Energized Seal Ring Performance Under Reciprocating Motion［D］.Wuxi：Jiangnan University， 2023.

［10］? 梁鶴， 王騰飛， 王文中， 等. 表面粗糙度對橡塑O形圈往復密封性能的影響［J］. 潤滑與密封， 2024， 49（2）：26-35.

LIANG He， WANG Tengfei， WANG Wenzhong， et al. Effect of Surface Roughness on Reciprocating Sealing Performance of Rubber O-ring［J］. Lubrication Engineering， 2024， 49（2）：26-35.

［11］? 閆曉亮， 杜曉瓊， 常凱，等. 表面粗糙度對航空液壓作動器密封性能的影響［J］. 航空工程進展， 2020， 11（5）：738-745.

YAN Xiaoliang， DU Xiaoqiong， CHANG Kai，et al. Influence of Surface Roughness on Seal Property of Aircraft Actuator［J］. Advances in Aeronautical Science and Engineering，2020，11（5）：738-745.

［12］? 史艷玲， 李丹， 朱艷紅， 等. 核泵橡膠密封圈貯存期的預測［J］. 特種橡膠制品， 2021， 42（6）：52-55.

SHI Yanling， LI Dan， ZHU Yanhong， et al. Prediction of Storage Life of Rubber Sealing Ring of Nuclear Pump［J］. Special Purpose Rubber Products， 2021， 42（6）：52-55.

［13］? LIU Jie， LI Xiangbo， XU Likun， et al. Service Lifetime Estimation of EPDM Rubber Based on Accelerated Aging Tests［J］. Journal of Materials Engineering and Performance， 2017， 26（4）：1735-1740.

［14］? 郭明達. 電連接器用聚氨酯膠密封件性能退化建模與試驗評估研究［D］. 杭州：浙江理工大學， 2022.

GUO Mingda. A Study on Modeling， Testing and Evaluation of Performance Degradation of Polyurethane Sealing Elements for Electrical Connectors［D］. Hangzhou：Zhejiang Sci-tech University， 2022.

［15］? 潘駿， 張雯， 張利彬， 等. 電連接器接觸件振動可靠性試驗評估［J］. 機械工程學報， 2021， 57（10）：257-266.

PAN Jun， ZHANG Wen， ZHANG Libin， et al. Vibration Reliability Test Assessment of Electrical Connector Contacts［J］. Journal of Mechanical Engineering， 2021， 57（10）：257-266.

［16］? 崔昌， 石偉偉， 胡珊珊， 等. 基于磨損量正態(tài)分布刀具可靠性模型及驗證［J］. 廣西大學學報（自然科學版）， 2020， 45（6）：1378-1385.

CUI Chang， SHI Weiwei， HU Shanshan， et al. Reliability Analysis of Diamond Drills Based on Distribution of Wear Degradation［J］. Journal of Guangxi University（Natural Science Edition）， 2020， 45（6）：1378-1385.

［17］? 錢萍， 陳文華， 高亮， 等. 航天電連接器綜合應力可靠性統(tǒng)計模型的驗證［J］. 中國機械工程， 2011， 22（3）：257-261.

QIAN Ping， CHEN Wenhua， GAO Liang， et al. Reliability Statistical Model Verification of Aerospace Electrical Connectors under Multiple Stresses［J］. China Mechanical Engineering， 2011， 22（3）：257-261.

［18］? 劉涼冰. 聚氨酯的化學降解［J］. 彈性體， 2003（1）：53-56.

LIU Liangbing. The Chemical Degradation of Polyurethane［J］. China Elastomerics， 2003（1）：53-56.

［19］? 虎龍， 李宗家， 陳虹， 等. 聚醚聚氨酯膠黏劑濕熱老化機制研究［J］. 合成纖維， 2023， 52（5）：6-11.

HU Long， LI Zongjia， CHEN Hong， et al. Mechanism of Wet Heat Aging of Polyether Polyurethane Adhesive［J］. Synthetic Fiber in China， 2023， 52（5）：6-11.

［20］? ZAIN N M， AHMAD S H， ALI E S. Durability of Green Polyurethane Adhesive Bonded Aluminum Alloy in Dry and Hydrothermal Ageing Conditions［J］. Journal of Applied Polymer Science， 2014， 131（23）：41151.

［21］? LIN Y， LIN Y F， HSIAO C. Evaluation of Bond Quality at the Interface between Steel Bar and Concrete Using the Small-dimension Break-off Test［J］. Materials and Structures， 2010， 43（5）：583-595.

［22］? WANG Xiaowei， REN Jiaxing， HU Xinyu， et al. Meso-scale Adhesive/Cohesive Failure Behaviors of Porous Asphalt Mixtures Considering Random Inhomogeneous Distribution of Binder［J］. Construction and Building Materials， 2023， 403：133097.

［23］? 戴樹森. 可靠性試驗及其統(tǒng)計分析［M］. 北京：國防工業(yè)出版社，1984.

DAI Shusen. Reliability Test and Statistical Analysis［M］. Beijing：National Defense Industry Press， 1984.

［24］? 王波， 矯桂瓊， 賴東方， 等. 真空結(jié)構(gòu)橡膠密封圈的泄漏率分析［J］. 西北工業(yè)大學學報， 2010， 28（1）：129-133.

WANG Bo， JIAO Guiqiong， LAI Dongfang， et al. Applying Roth Theory to Calculating Leak Rate of Rubber Gasket of Structure in Vacuum［J］. Journal of Northwestern Polytechnical University， 2010， 28（1）：129-133.

［25］? 錢夢騄， 王浩. 粘接界面的氫鍵模型與彈簧邊界條件［C］∥中國聲學學會2006年全國聲學學術(shù)會議論文集. 廈門， 2006：2.

QIAN Menglu， WANG Hao. Hydrogen Bonds and Spring Boundary Conditions at Bonding Interface［C］∥ Proceedings of the 2006 National Acoustical Conference of the Acoustical Society of China. Xiamen：2006：2.

［26］? 王建華， 賴益梁， 袁燕， 等. 基于橡膠瀝青粘彈試驗測定模型參數(shù)優(yōu)化研究［J］. 粘接， 2023， 50（7）：59-63.

WANG Jianhua， LAI Yiliang， YUAN Yan， et al. Parameter Optimization Study on Determining Model Based on Viscoelastic Test of a Asphalt Rubber［J］. Adhesion， 2023， 50（7）：59-63.

［27］? 中華人民共和國第四機械工業(yè)部. 恒定應力壽命試驗和加速壽命試驗方法總則：GB 2689.1—1981［S］. 北京：國家標準總局，1981：10.

The Fourth Ministry of Machinery Industry of the Peoples Republic of China. General Rules for Constant Stress Life Test and Accelerated Life Test：GB 2689.1—1981［S］. Beijing：State Administration of Standards，1981：10.

［28］? 李莉， 張賽， 何強， 等. 響應面法在試驗設(shè)計與優(yōu)化中的應用［J］. 實驗室研究與探索， 2015， 34（8）：41-45.

LI Li， ZHANG Sai， HE Qiang， et al.Application of Response Surface Methodology in Experiment Design and Optimization［J］. Research and Exploration in Laboratory， 2015， 34（8）：41-45.

［29］? 中華人民共和國機械電子工業(yè)部. 電連接器試驗方法：GJB 1217—1991［S］. 北京：國防科學技術(shù)工業(yè)委員會，1991：10.

Ministry of Machinery and Electronics Industry of the Peoples Republic of China. Test Methods for Electrical Connectors：GJB 1217—1991［S］. Beijing：Commission of Science， 1991：10.

［30］? 中華人民共和國電子工業(yè)部. D系列矩形連接器總規(guī)范：GJB 142—1986［S］. 北京：國防科學技術(shù)工業(yè)委員會，1986：10.

Ministry of Electronics Industry of the Peoples Republic of China. General Specification of D Series Rectangular Connectors：GJB 142—1986［S］. Beijing：Commission of Science， 1986：10.

［31］? 王沿朝， 陳清軍. 基于粒子群優(yōu)化算法的軟土場地Davidenkov模型參數(shù)擬合與應用［J］. 振動與沖擊， 2019， 38（17）：8-16.

WANG Yanchao， CHEN Qingjun. Parametric Fitting of Soft Soil Sites Davidenkov Model Based on PSO Algorithm and Its Application［J］. Journal of Vibration and Shock， 2019， 38（17）：8-16.

［32］? 紀震. 粒子群算法及應用［M］. 北京：科學出版社，2009：19.

JI Zhen. Particle Swarm Optimization Algorithm and Its Applications［M］. Beijing：Science Press， 2009：19.

［33］? 梅長林，周家良. 實用統(tǒng)計方法［M］. 北京：科學出版社， 2002：1-18.

MEI Changlin， ZHOU Jialiang. Practical Statistical Method［M］. Beijing：Science Press， 2002：1-18.

［34］? 汪榮鑫. 數(shù)理統(tǒng)計［M］. 西安：西安交通大學出版社，1986：266-280.

WANG Rongxin. Mathematical Statistics［M］. Xian：Xian Jiaotong University Press，1986：266-280.

［35］? 蔡花， 王惠民， 賈心緣， 等. AD正態(tài)性檢驗在HBsAg內(nèi)部質(zhì)量控制中的應用［J］. 現(xiàn)代預防醫(yī)學， 2016， 43（23）：4373-4377.

CAI Hua， WANG Huimin， JIA Xinyuan， et al. AD Normality Test in Internal Quality Control of HBsAg［J］. Modern Preventive Medicine， 2016， 43（23）：4373-4377.

［36］? 張世強. 曲線回歸的擬合優(yōu)度指標的探討［J］. 中國衛(wèi)生統(tǒng)計， 2002（1）：9-11.

ZHANG Shiqiang. Discussion on Goodness of Fit Index of Curve Regression［J］. Chinese Journal of Health Statistics， 2002（1）：9-11.

［37］? 沈鶴飛， 韓曉輝， 尹承澤， 等. 聚氨酯膠與玻璃界面粘接分子動力學研究［J］. 中國膠粘劑， 2023， 32（6）：26-31.

SHEN Hefei， HAN Xiaohui， YIN Chenze， et al. Molecular Dynamics Study on the Bonding of Polyurethane Sealant to Glass Interface［J］. China Adhesives， 2023， 32（6）：26-31.

（編輯? 胡佳慧）

作者簡介：

錢? 萍， 女， 1983 年生，副教授。研究方向為可靠性試驗與統(tǒng)計分析。E-mail： qianping@zstu.edu.cn。