喀斯特山區TRMM降水數據降尺度研究

謝伊娜 張洪波 張潤云 孔功 趙孝席

摘 要：獲取高精度的衛星降水數據，為喀斯特區域旱澇災害評估、水文預報等各研究領域提供數據基礎。以熱帶降雨衛星（tropical rainfall measuring mission，TRMM）為數據源，采用多元線性回歸法（ordinary least square，OLS）和地理加權回歸法（geographically weighted regression，GWR），綜合考慮高程、坡度、坡向、經緯度和歸一化植被指數（normalized difference vegetation index，NDVI）等6個因子構建OLS和GWR降尺度模型進行年降尺度研究，并比較OLS和GWR兩種降尺度模型在喀斯特山區的適用性。結果表明：1）TRMM數據與站點觀測數據之間精度較好；2）降尺度后數據空間分辨率提升到1 km，GWR降尺度年降水量在多數年份比原始TRMM數據更接近實測值，高估現象得到改善；與OLS降尺度數據相比，其三項指標表現更好；3）單站點中，OLS降尺度數據在高程和NDVI突變區域易出現假性更優相關性。綜合多指標評價，GWR降尺度數據在喀斯特山區總體精度更高。后續可通過劃分植被區、巖溶區、增加環境因子、校正等使降水更貼合實測值。

關鍵詞：TRMM 3B43；降尺度；GWR模型；喀斯特山區

中圖分類號：P426.6；P333

文獻標志碼：A

降水是全球水文循環的重要部分，已成為與氣候分析、水資源評價、水循環和水文模型等相關研究中不可或缺的關鍵參數［1］，其精度和時空分辨率決定以上研究過程分析的準確性［2］。傳統降水數據資料多基于氣象站點觀測，通過點插值成面來獲取［3］，在站點稀疏、地形復雜的山區，插值結果往往誤差很大［4］。獲取高空間分辨率和高精度的降水資料對于干旱監測、水土防治和水資源規劃等具有重要的現實意義［5］。

遙感衛星類降水數據觀測范圍廣、時空連續性好、不受地形和氣候條件局限，在獲取降水數據的時空分布方面具有明顯的優勢［2］，其中熱帶降雨衛星（tropical rainfall measuring mission，TRMM）在干旱監測［6］、洪水預報［7］、水文模型［8］等方面都得到了廣泛應用，但在區域降水高分辨率時空變異特征研究需求不斷提升的背景下，TRMM數據0.25°的空間分辨率略顯粗糙［9］。近年來，IMMERZEEL等［10］首次將歸一化植被指數（normalized difference vegetation index，NDVI）作為單一輔助變量，對TRMM數據進行降尺度，獲得了較為可靠的結果。JIA等［11］同時考慮了高程（digital elevation model，DEM）和NDVI，構建與降水的多元線性回歸（ordinary least square，OLS）模型，對TRMM降尺度后精度顯著提升。XU等［12］基于空間異質性的地理加權回歸模型（geographically weighted regression，GWR），將DEM和NDVI作為輔助變量成功將TRMM降尺度至1 km。總結發現，多元回歸模型OLS和考慮空間異質性的GWR模型均能不同程度地提高TRMM的空間分辨率，且降尺度研究趨于綜合考慮更多環境因子。

西南喀斯特山區是長江和珠江上游生態屏障的重要組成部分，其地形和氣候復雜，水土流失嚴重，洪水和干旱頻發，獲取其準確且高精度的降雨格局對喀斯特山區生態環境恢復至關重要［13］。國內外對TRMM數據的降尺度研究多在地勢平坦的平原、盆地以及西北部等地區，而對于西南部的喀斯特山區針對性研究較少［10-12］。貴州省是西南喀斯特山區中唯一一個沒有平原支撐的省份［14］，在貴州省開展TRMM降尺度研究具有典型性。曾業隆等［15］考慮了地形起伏度這單一輔助變量對TRMM構建GWR降尺度模型，發現背風坡地形起伏對降水的積極關系可能不存在；姬世保等［16］對TRMM降尺度到0.05°，未考慮DEM對降水的影響；吳健等［17］構建了降水與DEM、坡度、坡向和經緯度等地形因子的多元線性回歸模型來降尺度，未考慮植被的影響。降水的空間分布與地理位置、地形、植被等因素都息息相關，目前在喀斯特山區TRMM降尺度研究輔助變量的選取都只考慮了植被因子或者部分地形因子，同時直觀比較線性回歸方法和GWR方法降尺度效果的較少。

本研究將以喀斯特山區發育的貴州省作為研究區，同時引入NDVI、DEM、坡度、坡向、經度和緯度等植被和地理地形輔助變量，借助能綜合考慮多因素的多元線性回歸模型（OLS）以及能考慮降水與影響因子間非平穩關系的GWR模型ADDIN[18]，對TRMM降尺度到1 km，并對比兩種降尺度方法在研究區的適用性，以期為今后獲取喀斯特山區高空間分辨率降水提供方法借鑒，并為區內降水分布、水土保持、干旱監測等研究提供數據支撐。

1 研究區概況

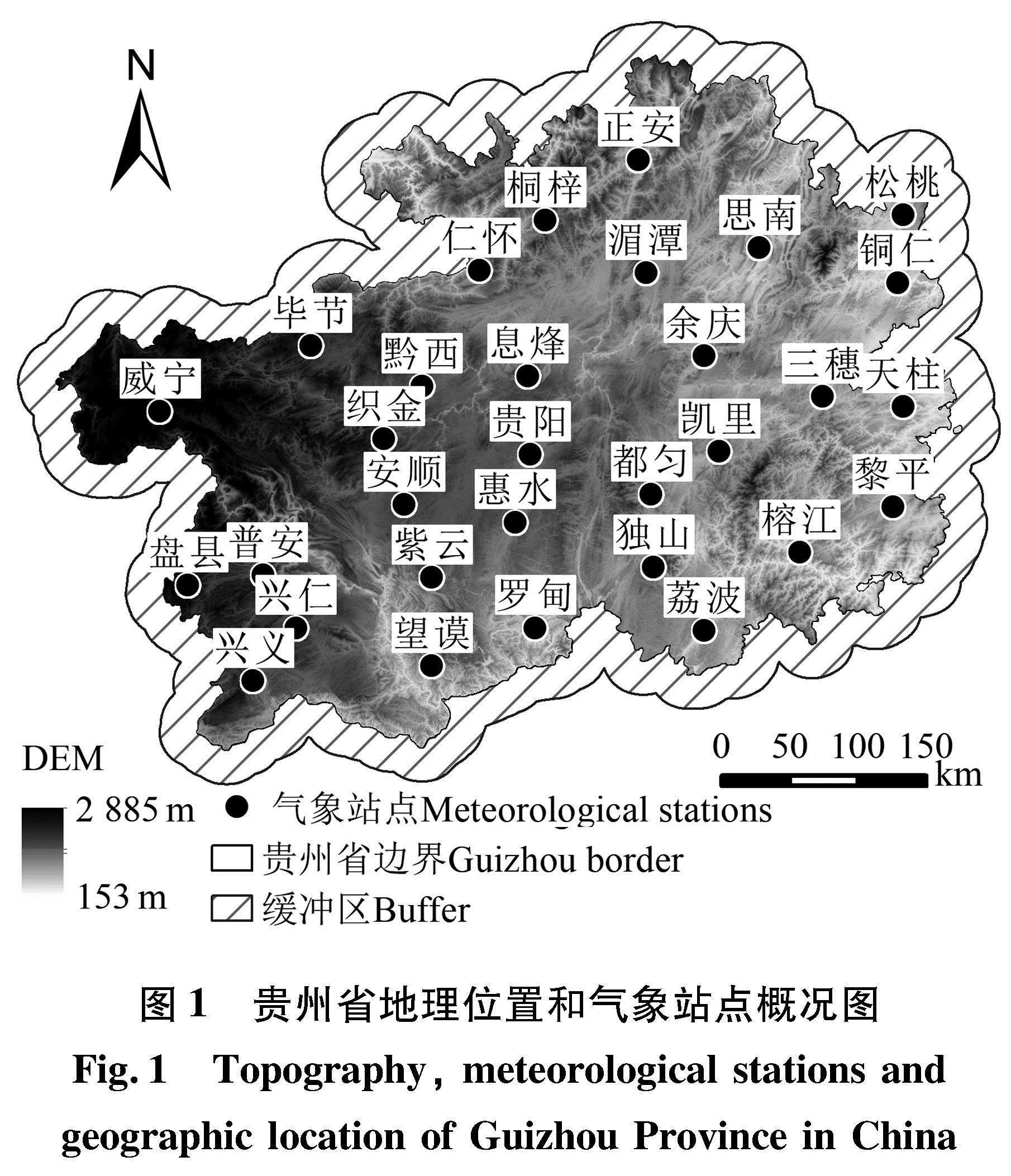
貴州省位于我國西南地區，介于東經103°36′～109°35′、北緯24°37′～29°13′之間，是世界上最大的喀斯特地貌集中分布區，全省面積1.761×105 km2，喀斯特地貌占73.8%，構成獨特的巖溶生態系統［19］。貴州地處云貴高原東側、青藏高原東南坡，平均海拔1 100 m左右，地勢西高東低，92.5%為山地和丘陵，有大婁山、苗嶺、武陵山和烏蒙山，地形地勢復雜。主要為亞熱帶濕潤季風氣候，年平均氣溫15 ℃，年降水量約1 300 mm，集中在4—9月，氣候呈多樣性，降水量時空分布復雜［20］。為提高降尺度處理過程中的精度，對研究區邊界向外做一個TRMM像元（25 km）的緩沖區進行分析（圖1）。

2 數據與研究方法

2.1 數據

2.1.1 地面氣象站點數據

本研究使用的2008—2019年31個地面氣象站點實測降水日值數據集來源于國家氣象科學數據中心（http：//data.cma.cn/），站點分布見圖1。

2.1.2 遙感數據

TRMM是美國宇航局和日本宇宙航空研究開發機構的一個聯合項目，提供了一系列具有不同空間和時間分辨率的降水數據集［12］。本研究采用2008—2019年TRMM 3B43 最新版本（V7）逐月降水資料，空間分辨率為0.25°×0.25°（約25 km×25 km），來源于NASA網站（http：//mirador.gsfc.nasa.gov/）。

NDVI數據來自TERRA衛星上中分辨率成像光譜儀傳感器的MODIS 13A3 V006版本產品（https：//lasweb.modaps.eosdis.nasa.gov/），空間分辨率為1 km×1 km的逐月合成數據，選取2008—2019年。

DEM數據來源于中國科學院資源環境科學與數據中心（https：//www.resdc.cn/），是美國航空航天局和國家測繪局聯合測量的SRTM數據集，考慮到本研究的空間尺度，下載空間分辨率為90 m和1 km的DEM柵格數據，坡度、坡向和經緯度從中提取。

2.1.3 數據預處理

地面氣象站點日值數據利用MATLAB單位轉換和累加求和，獲得31個站點實測年降水數據；對TRMM降水數據利用ENVI和ArcGIS軟件經過波段提取、旋轉、添加地圖信息、投影轉換、單位轉換、提取多值到點和累加求和獲得年尺度的原始TRMM降水數據；MODIS 13A3數據進行波段提取、投影轉換、鑲嵌、裁剪、去負值和無效值剔除，并通過對每年的月值柵格數據集求平均得到年平均NDVI數據，坡度、坡向從DEM數據中提取。

2.2 研究方法

2.2.1 普通最小二乘法

普通最小二乘法［21］（OLS）屬于全局多元線性回歸方法，對相關變量進行數學擬合、最小化誤差平方和后得出估計值，其中，相關解釋變量對因變量的作用程度在研究區域一致，公式［22］為

式中：i=1，2，…，N，N和i分別為像元數量和自變量個數；yi為第i像元的因變量；xij為第i像元的第j個解釋變量（坡度、坡向、海拔、經緯度和NDVI）；β0是回歸參數常數項；εi是第i像元的回歸殘差估計值，對應變量的系數在整個研究區內一致；βj為第j個解釋變量的回歸系數。

2.2.2 地理加權回歸模型

地理加權回歸模型（GWR）是一種能反映空間變化異質性的局部加權回歸模型［18，23］，將空間權重引入地理位置函數，以表征變量之間的空間依賴度，遵循Tobler“地理學第一定律”［24］，即空間距離越近相關性越大。采用Akaike準則（Akaike information criterion，AIC）確定最優帶寬，將每個目標要素最優帶寬范圍內的因變量和解釋變量進行整合，從而對研究范圍內任意位置空間格點相關變量進行局部擬合，每個格點自變量回歸系數不一致，基本模型［25］為

式中：（ui，vi）是第i像元中心點的經緯度，考慮模型需求，采用Albers投影坐標；β0（ui，vi）是第i像元基于位置函數的回歸參數常數項；ε（ui，vi）是第i像元基于位置函數的殘差估計值；βj（ui，vi）為第j個影響因子對第i像元的線性回歸參數。回歸參數

式中：dij是像元i和j之間的距離；b為自適應帶寬大小，即最優帶寬。

2.2.3 降尺度方法

基于GWR和OLS模型，建立TRMM 3B43降水數據與解釋因子之間的函數關系來進行降尺度：

1）數據集準備：從原始TRMM數據中提取每個像元的經緯度（ui，vi）和降水值yL，i（L表示0.25°低分辨率數據，H表示1 km高分辨率數據），將解釋因子xij分別重采樣至0.25°（xL，ij）和1 km（xH，ij）；

2）建立回歸關系：將步驟1）中的低分辨率數據集分別輸入兩個模型，建立0.25°分辨率下TRMM 數據yL，i與xL，ij的回歸關系，得到低空間分辨率下自變量的系數βL，j、常數項βL，0和殘差項εL；

3）數據柵格化：將0.25°空間分辨率的系數βL，j、常數項βL，0等點轉面，分別重采樣至1 km高分辨率的βH，j和βH，0， OLS為全局回歸模型，遂βH，j和βH，0與低分辨率下保持一致，對兩種模型的εL通過簡單克里金插值［25］，得到高分辨率的殘差值εH；

4）回代模型：基于GWR和OLS模型，將研究區高分辨率下所有像元的βH，j、βH，0、εH和xH，ij回代第2步中，得到空間分辨率為1 km的降尺度降水數據。

2.2.4 精度評價指標

以實測站點數據為真值，選擇皮爾遜相關系數（Pearson correlation coefficient，CC）、相對誤差（relative error，RE）和均方根誤差（root mean square error，RMSE）3個統計指標，對降尺度前后TRMM衛星降水數據進行精度驗證，公式［26］為：

相關系數：

式中：Tt為TRMM降水產品降水量；t為TRMM降水產品降水量均值；Pt為實測站點降水量，t為實測站點降水量均值；M為樣本數。

3 結果與分析

3.1 原始TRMM數據適用性分析

原始TRMM數據相對于氣象站點實測數據在時空分布上存在一定偏差，對其進行適用性分析是降尺度結果具有可靠性的前提。在年時間尺度上，以2008—2019年31個地面站點年實測數據為自變量，對應時間序列的TRMM 3B43降水數據為因變量構建一元線性函數。由圖2可知，相關系數為0.763 9，其通過P<0.000 1的顯著性檢驗，相對誤差為3.50%，均方根誤差為179.397 mm，TRMM數據年降水量在一定程度上比實測數據稍微偏大，與站點觀測數據在年尺度上整體存在明顯的相關性且適用性較高。

整體相關性程度表征不出單站點精度高低，對研究區31個氣象站點下TRMM和年實測數據之間的CC構建泰勒多邊形（圖3）。從圖3可看出，所有站點的CC都在0.6以上，最高達0.95左右，且有一半站點的CC大于0.8，西南部相關系數整體優于東北部，31個站點都通過了0.05的顯著性檢驗，其中研究區26個地面氣象站在P<0.01水平下顯著，說明在各站點下兩種數據也具有較好的相關性，精度較高，總體滿足TRMM年數據降尺度研究的需要。

3.2 TRMM降尺度結果及驗證

3.2.1 年降水量降尺度結果及驗證

利用GWR和OLS兩種降尺度模型將空間分辨率為0.25°的TRMM衛星降水數據成功降尺度到1 km，將2008—2019年的原始TRMM 3B43年降水數據、GWR模型降尺度后年降水數據和OLS模型降尺度后年降水數據求平均，得到多年平均降水量（圖4）。可知：1）降尺度后的TRMM空間分辨率提升到1 km，空間細節表現增強，邊緣過渡較平滑； 2）GWR降尺度的降水量在數值上更接近原始TRMM，OLS降尺度后的降水量最高值遠大于降尺度前，這是由于OLS將各輔助變量影響程度整體化平均化，易出現局部異常；3）整體上，GWR得到的降水量在空間格局上更能反映原始TRMM降水，兩者在空間分布上趨向一致，自西北向東南逐漸增加，東南部為多雨區，西北部偏少，與實際降水分布情況一致。而多雨區形成的主要原因是貴州省東部易受到印度季風槽前西南暖濕氣流東擴影響，同時北高南低的傾斜地形對偏南暖濕氣流有抬升作用［27］。OLS降尺度模型得到的降水量在研究區內沒有明顯降水分區。

對2008—2019年GWR和OLS模型降尺度后的數據進行年相關性分析（表1），GWR降尺度數據的CC為0.716，OLS為0.528，都通過了0.000 1的顯著性檢驗，前者較后者CC提高了0.188，RE降低了23.80%，RMSE減少了261.839 mm；與原始TRMM相比，GWR數據的相關系數略低，相對誤差更接近0。GWR模型降尺度的年降水精度整體高于OLS降尺度的年降水，主要是由于OLS為全局回歸模型，認為對應解釋變量對降水的影響作用在研究區一致，未考慮空間異質性，易產生偏差。

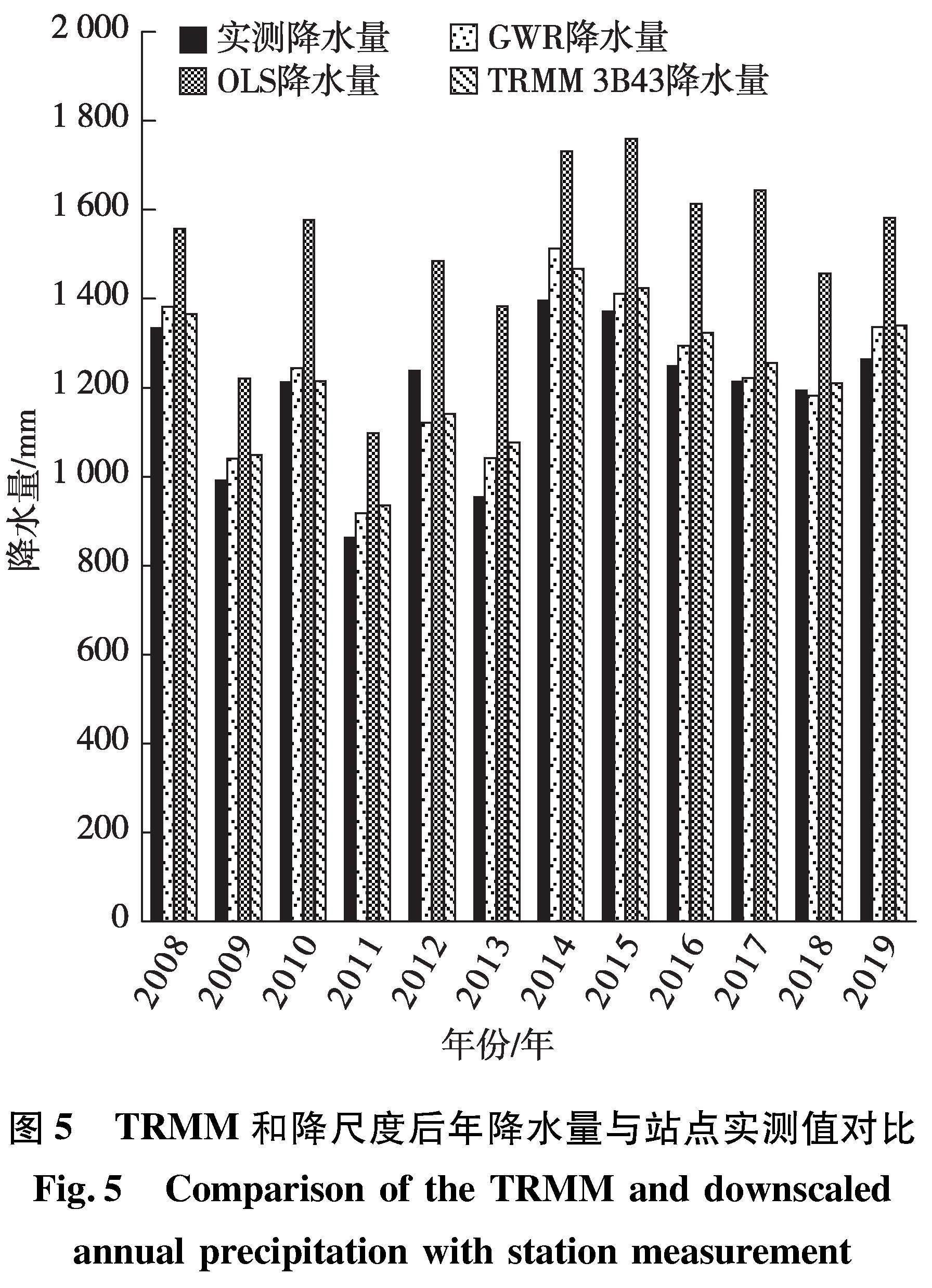
另外發現（圖5），研究區近12年降尺度前后和實測降水數據變化趨勢基本一致。與實測數據相比，OLS模型降水普遍存在大幅度高估，特別是2017年高于實測值429.256 mm；原始TRMM降水數據2010年與實測數據基本持平，2012年小于實測值，其他年份小幅度高于實測降水；經GWR模型降尺度后的降水估算值在TRMM降水易發生高估的多數年份里（2009、2011、2013、2015、2016、2017、2019）更接近實測值，減小了偏離程度。

3.2.2 單站點降水量降尺度結果及驗證

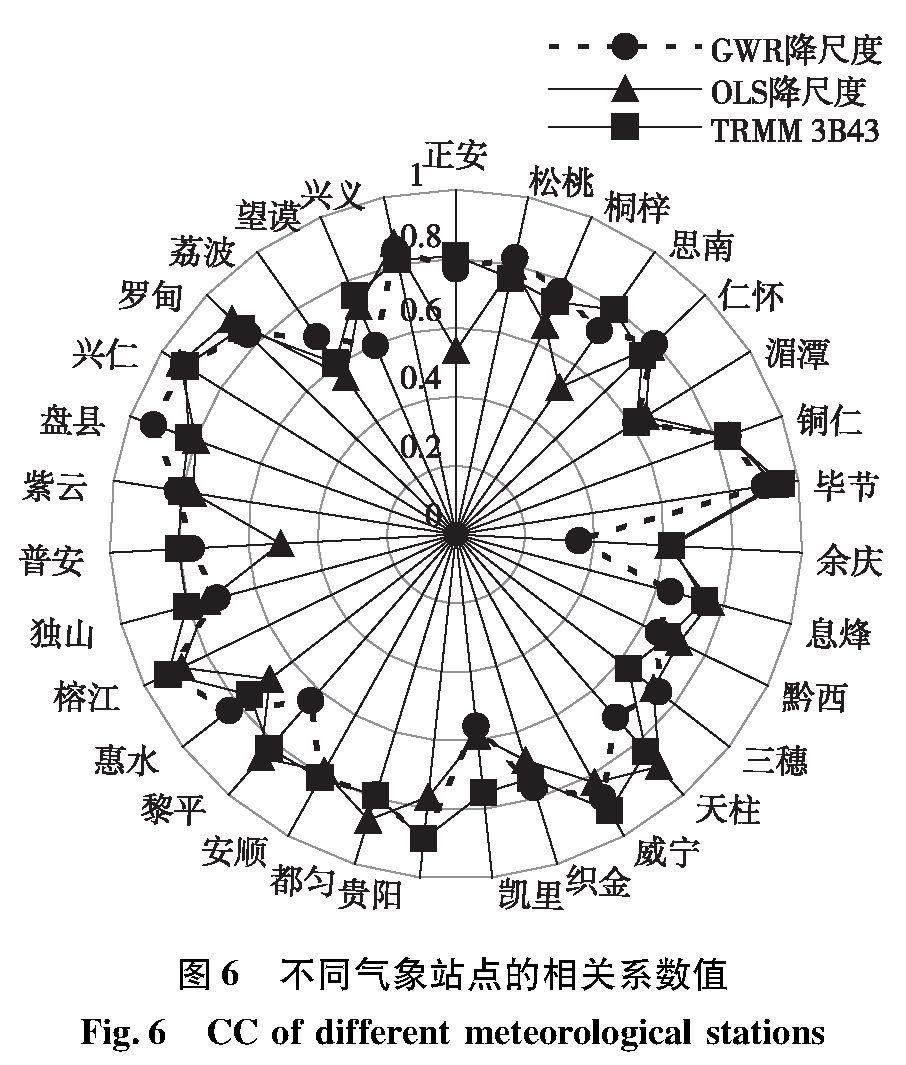
分別對貴州省近12年的GWR和OLS模型降尺度年數據、原始TRMM降水年數據按站點進行精度驗證。從皮爾遜相關系數指標看（圖6），三種降水數據相關系數值在各站點整體較高，原始TRMM和降尺度后CC都大于0.7的有16個站點，其中銅仁、畢節、威寧、榕江、興仁、羅甸和興義高于0.8，畢節和興仁在0.9以上；GWR降尺度后余慶較其他站點更低，松桃、桐梓、仁懷、銅仁、三穗、織金、惠水、紫云、盤縣、荔波和興義等11個站點較原始TRMM 3B43均有所提高，其中盤縣從0.81提高到0.93；OLS降尺度后松桃、湄潭、仁懷等12個站點比降尺度前略高，普安站較降尺度前降低了0.3，提高幅度普遍小于GWR數據。

降尺度前后大部分站點降水量存在高估現象（圖7），OLS數據高估程度尤為明顯，27個站點相對誤差值都大于GWR降尺度數據和原始TRMM數據；GWR降尺度數據接近一半站點RE值小于原始TRMM數據，高估現象在一定程度上得到了改善。原始TRMM數據與GWR數據的均方根誤差大多介于100～300 mm之間（圖8），OLS數據的RMSE變化波動較大，正安站高達1 276.8 mm。基于GWR模型降尺度后，思南、三穗、貴陽、惠水、荔波、興義等站點的RMSE均有所減小。

值得關注的是，DEM和NDVI突變區域（DEM變化絕對值在200～330 m左右，NDVI變化絕對值在0.2～0.4左右）內的15個站點（按站點順序湄潭—黔西、天柱、凱里、都勻、黎平、興仁、羅甸、望謨、興義）降尺度數據中，相比GWR降尺度得到的降水數據，OLS降尺度數據的RE和RMSE更大，但在相關系數這一指標上表現更優。這可能是由于OLS的全局平穩性會掩蓋地形和植被突然變化所產生的影響，將其平均化，從而出現假性的更優相關性，累積誤差和相對誤差實際卻更大，甚至遠超GWR降尺度數據的誤差。說明比較降尺度算法時，若只看相對系數這單一評價指標，可能會出現假性更優，因此需多指標綜合驗證。

4 結論與討論

4.1 結論

1）與實測站點觀測降水比較，TRMM 3B43衛星年降水量相對誤差在0.03左右，相關系數為0.764，一半以上站點CC大于0.8，在貴州省有較好的精度，表現出一定適用性。

2）經OLS和GWR模型降尺度后的數據，空間分辨率大幅提高，細節增多。相比OLS降尺度數據，考慮了空間異質性的GWR模型降尺度數據空間分布與原始TRMM更趨于一致，降水量與實測情況相符，呈現自東南向西北遞減的分布特征。

3）在年尺度上，相比于OLS降尺度數據，GWR降尺度模型得到的年降水在原始TRMM降水易發生高估的多數年份里更能刻畫真實降水，偏離程度更小，并且在三種評價指標上都更優。

4）單氣象站點，降尺度后的相關系數大多在0.7～0.97之間，OLS降尺度數據的相對誤差和均方根誤差多數大于GWR降尺度降水，其中正安站均方根誤差高1 110 mm左右，但若只看相對系數這單一評價指標可能會出現假性更優。

4.2 討論

基于GWR和OLS模型，綜合考慮了植被、地理和地形因子的降尺度數據，空間分辨率得到了極大的提升，細節刻畫能力增強，這與竇世卿等［28］結合多元輔助變量對TRMM降尺度研究的結果一致。兩種降尺度模型綜合從評價指標和與實測降水量的變化趨勢來看，GWR模型對TRMM的降尺度效果優于OLS模型，更能反映真實的降水信息，提高分辨率的同時較好地保證了數據精度。在年尺度和31個單站點降尺度方面，GWR降尺度后的個別指標，相較原始TRMM數據有略微降低，這與竇世卿和李豪等［28-29］在長江流域和四川省的年降尺度評估結果相似。從根本上來說，本研究的降尺度方法是一種圖像超分辨率處理，處理后的圖像會有不同程度的細節失真［29］。技術方面，TRMM遙感反演降水受下墊面復雜度和對降水靈敏度的影響［15］，其反演準確性存在空間差異，原始TRMM數據的精度也是降尺度誤差來源之一，加上重采樣和殘差插值也存在不可避免的誤差。同時，降水、植被和地形之間復雜關系的構建，實測雨量站點的分布、密度和數量也會影響降尺度評估的結果。但降尺度并不說明相關系數一定要高于原始TRMM數據，它的最終目的是在提高降水空間分辨率的同時獲得相當的降水精度來滿足實際應用研究［29］。

貴州省喀斯特復雜地形的巖石裂隙發育程度、石漠化分布和部分降水快速補給地下溶洞的情況異于其他山區，同時年尺度上植被主要集中于東南部。針對上述特征，可以在區域上劃分是否是植被區和是否是溶洞、暗河出露區、引入與降水相關的解釋變量（如表征干旱的指數）、結合氣象站點觀測數據校正降尺度數據等來進一步提高降水精度，使其更貼合實測值。

參考文獻：

[1]NING S， ZHOU H W， ZHANG Z Y， et al. Precipitation scale effect of the TRMM satellite in Tianshan， China［J］. Journal of Mountain Science， 2023， 20（5）： 1349-1368.

［2］ 寧珊， 張正勇， 劉琳， 等. TRMM偏最小二乘降尺度降水模型在新疆不同地貌的適應性［J］. 農業工程學報， 2020， 36（12）： 99-109.

［3］ 嵇濤， 劉睿， 楊華， 等. 多源遙感數據的降水空間降尺度研究：以川渝地區為例［J］. 地球信息科學學報， 2015， 17（1）： 108-117.

［4］ 譚偉偉. 長江經濟帶衛星遙感降水數據空間降尺度研究［D］. 武漢： 武漢大學， 2020.

［5］ 金彩平. TRMM衛星降雨數據空間降尺度校準及應用研究［D］. 南寧： 廣西大學， 2018.

［6］ 胡鵬飛， 李凈， 王丹， 等. 基于MODIS和TRMM數據的黃土高原農業干旱監測［J］. 干旱區地理， 2019， 42（1）： 172-179.

［7］ LI L， HONG Y， WANG J，et al. Correction to： evaluation of the real-time TRMM-based multi-satellite precipitation analysis for an operational flood prediction system in Nzoia Basin， Lake Victoria， Africa［J］. Natural Hazards， 2017， 89（3）： 1495.

［8］ 范田億， 張翔， 黃兵， 等. TRMM衛星降水產品降尺度及其在湘江流域水文模擬中的應用［J］. 農業工程學報， 2021， 37（15）： 179-188.

［9］ 趙澤宇， 秦福瑩， 那音太， 等. 基于GWR模型降尺度模擬蒙古高原地區TRMM降水數據［J］. 中國農業氣象， 2023， 44（3）： 182-192.

［10］IMMERZEEL W W， RUTTEN M M， DROOGERS P. Spatial downscaling of TRMM precipitation using vegetative response on the Iberian Peninsula［J］. Remote Sensing of Environment， 2009，113（2）：362-370.

［11］JIA S， ZHU W， LV A， et al. A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and DEM in the Qaidam Basin of China［J］. Remote Sensing of Environment， 2011，115（12）：3069-3079.

［12］XU S， WU C， WANG L， et al. A new satellite-based monthly precipitation downscaling algorithm with non-stationary relationship between precipitation and land surface characteristics［J］. Remote Sensing of Environment， 2015，162：119-140.

［13］胡實， 韓建， 占車生， 等. 基于地理加權回歸模型的典型山地衛星反演降水產品降尺度研究［J］. 山地學報， 2019，37（3）：451-461.

［14］李威， 蔣平， 趙衛權， 等. TRMM衛星降水數據在喀斯特山區的適用性分析：以貴州省為例［J］. 水土保持研究， 2016， 23（1）： 97-102.

［15］曾業隆， 譚偉， 王超， 等. 基于GWR模型的貴州喀斯特山區TRMM 3B43降水資料降尺度分析［J］. 干旱氣象， 2018， 36（3）： 405-414.

［16］姬世保， 杜軍凱， 仇亞琴， 等. 基于星地融合數據的黔桂喀斯特山地降水時空分布［J］. 南水北調與水利科技， 2019， 17（6）： 28-36.

［17］吳健， 周秋文， 韋小茶， 等. TRMM降水產品在喀斯特地區的空間降尺度研究：以貴州省為例［J］. 人民珠江， 2019，40（6）：20-26.

［18］MC MILLEN D P. Geographically weighted regression： the analysis of spatially varying relationships［J］. American Journal of Agricultural Economics， 2004， 86（2）：554-556.

［19］吳小飄， 周忠發， 朱孟， 等. 典型喀斯特聚集區不同地貌類型干旱時空特征［J］. 水土保持研究， 2023， 30（1）： 336-347.

［20］丁立國. 貴州山地復雜地形下暴雨洪澇災害風險研究［D］. 南京：南京信息工程大學， 2022.

［21］冀曉娜， 徐金秀. 寧城縣旅游氣候舒適度評價及基于客流量的評價模型優化［J］. 內蒙古氣象， 2021（6）：28-32.

［22］曾禮， 高艷紅， 蔣盈沙， 等. 地形因子對華東地區降水影響的尺度效應研究［J］. 地球科學進展， 2022， 37（5）： 535-548.

［23］OSHAN T， LI Z， KANG W，et al. MGWR： a python implementation of multiscale geographically weighted regression for investigating process spatial heterogeneity and scale［J］. ISPRS International Journal of Geo-Information， 2019，8（6）： 269.

［24］TOBLER W R. A computer movie simulating urban growth in the Detroit region［J］. Economic Geography， 2016， 46： 234-240.

［25］ARSHAD A， ZHANG W， ZHANG Z，et al. Reconstructing high-resolution gridded precipitation data using an improved downscaling approach over the high altitude mountain regions of upper Indus Basin （UIB）［J］. Science of the Total Environment， 2021， 784： 147140.1-147140.18.

［26］曠蘭， 田茂舉， 李強， 等. 多源降水融合分析產品在重慶復雜地形下的精度評價［J］. 中國農業氣象， 2023，44（1）：71-81.

［27］羅寧， 許炳南， 文繼芬， 等. 貴州大氣降水的時空分布規律研究［J］. 貴州氣象， 2006（4）： 3-7.

［28］張寒博， 徐勇， 竇世卿， 等. 基于GWR模型的長江流域TRMM數據降尺度［J］. 水土保持研究， 2021，28（3）：149-155.

［29］李豪， 雷苑. 復雜地形下TRMM降水數據的降尺度研究：以四川省為例［J］. 中國農業氣象， 2019，40（10）：607-619.

Spatial Downscaling of TRMM Precipitation Data

in Karst Mountainous Area

Abstract：

This study obtains high-resolution satellite precipitation data to provide a data base for various research fields in karst regions such as drought and flood disaster assessment and hydrological forecasting. Taking tropical rainfall measuring mission as the data source， using the ordinary least square and geographic weighted regression， this study constructed downscaling model of precipitation with elevation， slope， aspect， longitude， latitude and normalized difference vegetation index for annual downscaling research. And the applicability of OLS and GWR downscaling methods in the karstic mountainous areas of Guizhou province was compared. The results were as follows. 1） The accuracy between TRMM data and station observations was good. 2） The spatial resolution of the downscaling data was greatly improved to 1 km. The GWR model downscaling annual precipitation was closer to the measured value of meteorological stations than the original TRMM data in most years， and the overestimation phenomenon was ameliorated. Compared with the OLS downscaling annual data， the three indicators of GWR downscaling data performed better. 3） At single station， OLS downscaling data tended to have spurious better correlations in cases where elevation and NDVI value changed suddenly. Based on comprehensive evaluation of multiple indicators， the accuracy of GWR downscaling data was generally higher in karst mountainous areas. The subsequent research can get the precipitation data closer with the measured data by dividing vegetation areas and karst areas， adding environmental factor， calibrating downscaling precipitation， and so on.

Key words：

TRMM 3B43; downscaling; GWR model; karst mountainous