例析數學思想方法在求解數列問題中的運用

王偉慧

數列是高考的一個重要考點，這部分內容主要以客觀題的方式呈現，或與函數、不等式等內容相結合，以綜合題的方式呈現.不過無論以哪種方式呈現，其中都蘊涵豐富的數學思想方法，因此在數列問題求解教學中，教師應重視學生數學思想方法的培養，讓學生可以站在更高的視角思考和解決問題，提高學生數學能力與素養.本文結合具體實例談談數學思想方法在數列中的運用，以期引起師生對數學思想方法的重視.

1.函數與方程思想的運用

數列是特殊的函數，因此在解決數列問題時，可以利用函數的一些知識、經驗、方法來研究.

例1 已知等差數列an的前n項和為Sn，且S10=100，S100=10.

（1）求S110；（2）當n取何值時，Sn有最大值？

評注：本題求解主要是將數列問題轉化為方程或函數問題，問題迎刃而解.在解題時，切勿盲目地套用，應關注已知和所求之間的內在聯系，運用合適的數學思想方法將其建立聯系，從而找到合適的切入點，快速地解決問題.

2.數形結合思想的運用

數形結合思想在解題中有著廣泛的應用，通過“數”與“形”的結合可以將問題向直觀化、簡單化轉化.

例2 已知an是等差數列，bn是等比數列，公比q>1且bi>0（i=1，2，3，…），若a1=b1，a9=b9，則a5與b5的大小關系是.

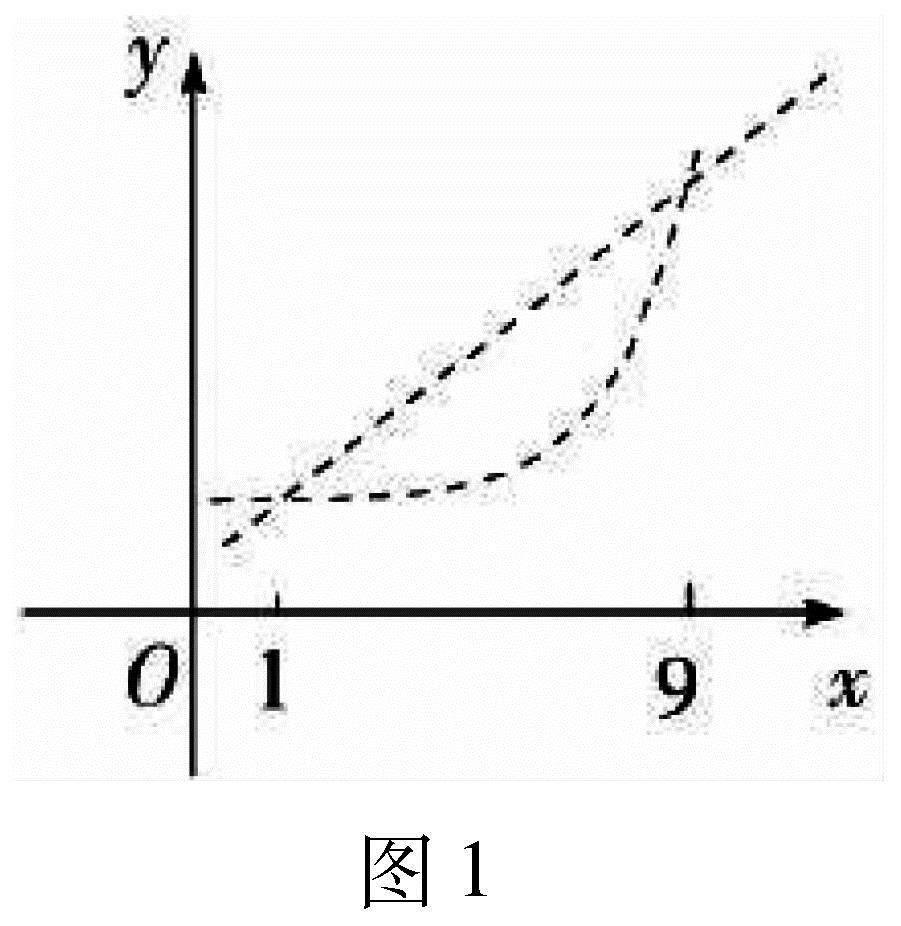
析解：從函數的視角出發，等差數列各項可以看作對應直線上一系列散點的縱坐標，而等比數列的各項可以看作是指數型函數圖象上一系列散點的縱坐標，這樣結合已知條件可以得到如圖1所示的圖形.根據圖形可知a5>b5.

評注：對比兩種解法不難發現，運用數形結合思想方法解題更高效.在平時教學中，教師應有意識地引導學生應用數形結合思想方法分析問題，由此提升學生數形結合意識.

3.分類討論思想的運用

分類討論是一種數學思想方法，也是一種解題策略，其在解題中有著重要的應用.

評注：在解題的過程中，經常會遇到由于存在不確定因素而需要分類的情況，如本題中的（－1）n，由于不確定n是奇數還是偶數而需要分類討論.若學生具有良好的分類討論意識，能夠靈活運用化特殊為一般的思想方法來分析問題，問題即可迎刃而解.

4.化歸思想的運用

化歸思想無處不在，它是分析和解決問題的有效路徑，是最基本、最常用、最重要的思想方法.在解題的過程中，通常會采用某些手段將陌生的、復雜的問題轉化為熟悉的、簡單的問題，從而快速地找到解題的突破口.

例4 設等差數列an的公差為d，點（an，bn）（n∈N*）在函數f（x）=2x的圖象上.

（1）若a1=－2，點（a8，4b7）在函數f（x）的圖象上，求數列an的前n項和Sn；

評注：轉化思想既是一種重要的數學思想方法，也是最重要的解題意識.在實際教學中，要重視這一重要數學思想方法的培養，從而逐步發展學生的數學核心素養.

5.整體思想的運用

在解題的過程中，將整體思想運用其中，可以起到降低解題難度，提升解題效率和解題準確率的作用.整體思想是從整體出發，充分挖掘題中各個條件之間的內在聯系，將那些看似無關而實質上有聯系的量看成一個整體，從而將復雜的題目簡單化，抽象的條件具體化，提高解題效率.

例5 在等比數列an中，S8=30，S16=150，求S20.

評注：本題求解中從整體視角出發，通過整體代入有效地優化了運算過程，有利于提升解題效率和解題準確率.

總之，數學思想方法是數學的靈魂，在日常教學中要不失時機地進行滲透，并創造機會讓學生去領會和感悟，以此讓學生可以獲得更高層次的理解，提升學生分析和解決問題的能力，提升學生數學核心素養.