解題教學中培養(yǎng)學生數學核心素養(yǎng)的實踐與思考

葉曉珍

眾所周知，數學核心素養(yǎng)是數學課程目標的重要組成部分.那么如何在課堂解題教學中既能讓學生有效地掌握教學內容，發(fā)展數學思維、提高能力，又能滲透各種核心素養(yǎng)的培養(yǎng)，便成了一種值得探究的問題.本文筆者通過自己開設的一節(jié)高三習題課就此問題談些不成熟的看法.

1 案例展示

在高三年級的一節(jié)研究性學習課上，筆者提出了一個問題，要求學生先自主探索再小組討論，并要求他們把解題中的思維過程真實的記錄下來，并在幻燈片給予展示，同時要求解題者加以解說.

幾分鐘之后，先后有幾個小組的同學舉手要求發(fā)言.

教師發(fā)現，有很多同學點頭表示贊同，但也有同學要求發(fā)言.

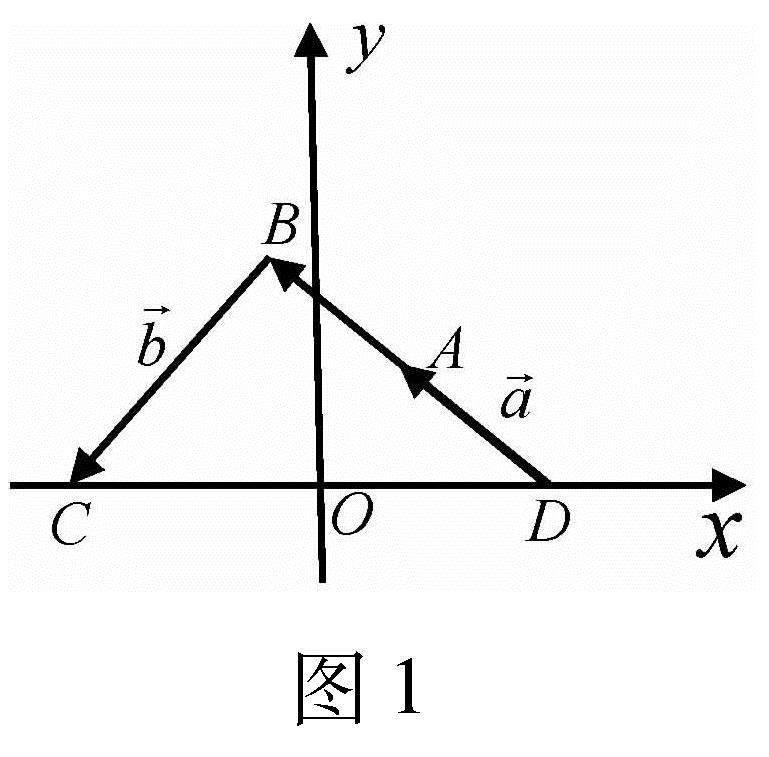
生2：我們組有同學在印象中接觸過類似的問題，具體思路如下：

師：現在出現了兩種不同的思路與解法，大家可以分組交流一下，然后進行適時評價.

經過幾分鐘交流之后，有幾個小組要求發(fā)言.

師：我觀察到很多同學在點頭表示贊成生3所在小組的觀點，但正如生3所言：我們既然知道這一漏洞，怎么去彌補呢？

師：很棒.生4所在小組發(fā)現了問題的關鍵點和突破口，那后續(xù)我們怎么利用這一個契機呢？

生5：我們小組想出來了一種后續(xù)的思路，具體如下：

也即利用cosθ≤1這一特性，從而求出了的正確范圍，因為最后答案與生2所在小組是一樣的，所以我們認為它是正確的.

同學們仔細檢查了以上解法，最后均表示沒有問題，并且鼓掌通過，然后教師讓同學們對以上解題情況加以總結.

生1：經過老師和同學們對我們解法的糾錯過程，我們小組認為：我們在解題中不能忽視數學知識或對象之間的相互聯(lián)系，否則解題就不可能獲得成功！

師：說的很好.我們每位同學在面對相同的數學問題時，頭腦中往往呈現出不同的解題策略.所以可能有些同學的想法不一樣，那么我們對上面這一問題還有其它解法嗎？

生6：我們小組想到可以利用數形結合思想來

師生一起仔細檢查了以上兩種解法，最后沒有發(fā)現問題.

師：很好.當然有些小組還沒有上來展示，可能是解法與上面的相同或類似，或者碰到了一些困難.下面請大家對以上的方法進行比較，談一下自己的感想.

生8：我們小組認為生2所在小組的方法更加簡單、實用;其次是生6與生7所在小組的方法，但這兩種解法要通過構造圖形來解決問題，有一定的思維難度;而生1所在小組的方法要得到正確答案的話，解題過程有點復雜且難以想到，感覺不是很好.

（教師看到有大多數的同學點頭贊成生8的觀點，少數沒有表示的同學也沒有發(fā)言）

師：很好.雖然我們經常說簡單就是美，簡潔美是數學美的主要特征之一，但是對于問題解決而言，首先是要解決問題，其次再追求解決過程及方法的簡潔化.故老師并不完全贊同生8所代表的部分同學的看法：即解題過程簡單就是最好的.

（教師看到大多數的同學點頭贊成，順勢提出下面的問題）

師：同學們，我們可以高屋建瓴看一下，上面的解法運用了哪些數學思想方法？

生9：生1與生2所在小組的解法主要利用了方程思想與三角函數法，生6與生7所在小組主要分別利用了坐標法與構圖解題法，這些實際上是用了轉化思想和數形結合思想.

師：好的，上面同學講的方法非常細到.固然，各個解法中并非絕對只用了某一種數學思想方法，它們之間有時也是相互滲透的.另外，老師想問一下：我們在以前多次提到數學核心素養(yǎng)，那么上面解法主要能夠培養(yǎng)我們同學哪幾種核心素養(yǎng)呢？

生10：由于老師以前給我們看過有關核心素養(yǎng)方面的講義，也上過有關這方面的選修課.所以我們還是有一定印象的.我們認為：顯然，數學抽象、邏輯推理與數學運算這三個核心素養(yǎng)肯定是滲透在課堂里面的，而最后兩種解法又凸顯出直觀想象核心素養(yǎng)，其它核心素養(yǎng)體現的不是非常明顯.”

師：看樣子我們在上課中或在課外時間接觸過核心素養(yǎng)的有關知識，其效果還是非常明顯的，同學從開始時的茫然不知到現在的娓娓到來，很棒！另外，將問題進行改編是我們研究數學問題經常運用的方法，下面請大家思考一下，能否把上面問題改編？

（改編數學問題同學們也并不陌生，花了一些時間就陸續(xù)展示了以下的部分若干成果）

師：很棒.由于時間關系，前面可能有些同學可以還沒有改編好，那么沒有改編好的問題請大家課外再加以解決.

（這節(jié)課的時間已到，老師布置了作業(yè)，宣布下課）

2 教學思考

2.1 解題教學是知識的不確定性到知識的確定性的漸進過程

教學應當是一種由知識的不確定性到知識的確定性的漸進過程.知識的不確定性階段是指提出問題和判斷問題，證偽在這一階段伴演著重要角色；知識的確定性階段是對知識的確認，證實在這一階段起著重要作用.證實性知識與證偽性知識相結合，是實現知識遷移和知識創(chuàng)新的必然選擇.以上面課例中的生1所在小組的解法為例，通過生3與生4這兩個小組的反思、生5這個小組的后續(xù)補充、再加上教師的適當評價，完成了這道解法的“證偽”過程.而生2、生6與生7這三個小組的解法展示與分析，也就從多個角度完成了對這道問題的“確認”過程：它適及到向量、三角、圓以及不等式等有關知識，當然也可以繼續(xù)進行知識延伸.

2.2 解題教學也是歸類分析、一題多解到一題多變的漸進過程

已有的研究表明：一個數學問題在同一個體的思維中完全可能具有多種不同的心理表征，它們分別突出了對象的某些（而不是全部）性質，而且，在不同的時刻或場合，所得到“激活”的通常又只是這些不同心理表征中的某一個.這說明主體在解題活動中可以利用模式識別策略根據具體情況，進行兩次甚至于多次問題歸類、調節(jié)，從而達到解題目的.

在本課例的教學中通過一題多變的教學手段，能使學生吃透知識的外延與內涵，讓他們掌握其內涵發(fā)展與外延變換，使其對知識能融會貫通，從而培養(yǎng)學生思維的深刻性，提高他們的分析問題、解決問題的能力.通過課例中的問題改編，層層推進，使學生對高中數學的認識和理解呈螺旋式上升，從而對知識的理解更加深刻，培養(yǎng)了學生思維的深刻性.一題多解、一題多變不僅增強了例題的使用價值，同時培養(yǎng)了學生的發(fā)散思維能力，挖掘出學生的創(chuàng)新潛力，形成探究意識，從而達到以一勝多的功效.

2.3 解題教學更應是指向核心素養(yǎng)發(fā)展的漸進過程

指向核心素養(yǎng)發(fā)展的教學，就是要摒棄單純的知識結果教學格式，將知識的產生和發(fā)展過程嵌入教學的過程之中，過程與結果相互整合、相得益彰.

在傳統(tǒng)的教學過程中，學生的思維極具定向性、專一性.而通過“歸類分析——一題多解——一題多變”的訓練，完成知識的不確定性到知識的確定性的過程，這樣恰好可以很好地克服學生的思維定式，同時也發(fā)散了學生的思維，是滲透數學核心素養(yǎng)的有效方法和途徑之一.在以上的問題情境中，我們可以看出：通過這種方式的解題教學，可以培養(yǎng)學生深入研究，交匯拓展，從多角度、多途徑、多知識點等方而尋求解決問題的思路與方法，真正達到開拓解題思路，提升解題能力，增強思維品質，促進深度學習，進而在解決問題的過程中才能逐步形成與發(fā)展、進而提升數學核心素養(yǎng).

當然，指向核心素養(yǎng)發(fā)展的數學課，顯然不能一蹴而就，而是應當將“核心素養(yǎng)”的種子落地生根在學生可以接受的肥沃的土壤上，然后循序漸進、層層深入，這樣才能真正包攬千里之外無限風光，完成既定的教學目標.