例談用一元二次方程求根公式解難題

袁祖軍

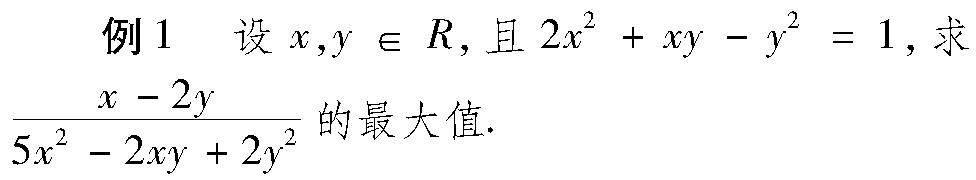
求根公式解含參一元二次方程，結果一般都比較繁（兩個根都是二次根式代數式），用于計算會更繁，往往被認為是笨拙的解法而不被看好，特別是難題，一般都不考慮用求根公式解決，其實，有些難題用求根公式解并不難，本文通過兩個例說明.

本題是一類常見的二元函數t=G（x，y）（F（x，y）=0）最值問題，通常的解法是技巧性很強的基本不等式法，即下面的解法1和解法2.

評注：上述解法1既有不好想的平方齊次化和“1”的巧代換，還有不好想的配湊均值不等式，更有取等條件的艱難確定，運算也未見簡單；解法2直接換元，消元化為一元顯函數，再換元化為簡單函數求最值，思路自然，但也不簡單.本題的自然直接的解法是用求根公式在約束條件方程中解出一元代入目標消元化為一元顯函數求最值，即下面的解法3.

評注：解法3是最自然（好想）的方法（直接在約束條件方程中用一元二次方程求根公式解出一元代入目標消元化為一元顯函數求最值，只要約束條件方程是可化為可解的二次方程（一次方程更不必說），在有導數知識下就總是可行的解法），且是本文三種方法中最簡單的.

例2 已知實數x，y滿足x2+2y2－xy=8，求x2+y2+xy的最大值.

用一元二次方程求根公式自然，簡單.

總之，二次方程總是可用求根公式（配方法結果）解的，判別式和基本不等式（均值不等式，柯西不等式，權方和不等式）都是x2≥0（x∈R）產生的（文［1］），所以，用求根公式解決二次方程問題是自然的，不一定是很繁的 ，有時還是最簡單的（文［2］），當技巧性的方法難想時，不妨先試試這個自然的方法.

參考文獻

［1］熊福州.再探一新母不等式的普遍意義與應用［J］，河北理科教學研究，2020（04）10-11.

［2］熊福州.也談解題應追求簡單、自然［J］，河北理科教學研究，2005（03）3-5.