基于ARIMA和LSTM的新能源汽車銷量預(yù)測研究

張鈺妍 張馨予

摘要：隨著全球能源結(jié)構(gòu)的轉(zhuǎn)變和環(huán)保意識的提升，新能源汽車行業(yè)迅速發(fā)展，銷量預(yù)測對于市場布局、生產(chǎn)及供應(yīng)鏈管理至關(guān)重要。然而，銷量預(yù)測受多種因素影響，具有復(fù)雜性和非線性特征，傳統(tǒng)的時間序列預(yù)測方法如ARIMA模型在處理這些特征時存在局限性。為克服這些問題，提出了一種創(chuàng)新的組合模型算法，該算法融合了ARIMA模型在捕捉線性趨勢方面的優(yōu)勢以及LSTM模型在捕捉非線性特征和時間依賴性方面的強大能力。利用選取的2021年1月—2023年9月每月新能源汽車銷售數(shù)據(jù)，驗證了該組合模型在預(yù)測未來一年內(nèi)兩個品牌新能源汽車銷量方面的準(zhǔn)確性和可靠性。研究結(jié)果表明，該組合模型相較于單一模型在預(yù)測精度上有所提升，RMSE下降約20%，為新能源汽車市場的戰(zhàn)略規(guī)劃提供了有價值的決策支持。

關(guān)鍵詞：ARIMA；LSTM；預(yù)測；新能源汽車

中圖分類號：U469.7? 收稿日期：2024-02-23

DOI：1019999/jcnki1004-0226202406007

1 前言

隨著全球能源結(jié)構(gòu)的轉(zhuǎn)變和環(huán)境保護(hù)意識的提高，新能源汽車行業(yè)迅速崛起，成為汽車市場的重要發(fā)展方向[1]。準(zhǔn)確的銷量預(yù)測對于新能源汽車企業(yè)的市場布局、生產(chǎn)計劃以及供應(yīng)鏈管理具有至關(guān)重要的意義。然而，新能源汽車銷量受到多種復(fù)雜因素的影響，如政策導(dǎo)向、技術(shù)進(jìn)步、消費者偏好以及市場競爭態(tài)勢等，從而使銷量預(yù)測成為一項極具挑戰(zhàn)性的任務(wù)。

在銷量預(yù)測領(lǐng)域，研究者已經(jīng)提出了多種方法。桂思思等[2]在2021年使用傳統(tǒng)的時間序列預(yù)測即ARIMA（自回歸積分滑動平均模型），有效地捕捉數(shù)據(jù)的線性趨勢，陳科秀等[3]在2022年使用同樣的方法對黑貓新能源汽車的銷量進(jìn)行研究，有效地捕捉了銷量的線性變化特征，并得出了有價值的預(yù)測結(jié)果。但隨著市場環(huán)境的不斷變化和消費者需求的多樣化，新能源汽車銷量的變化可能逐漸變得復(fù)雜，這使得單一的ARIMA模型無法處理這種非線性特征[4-5]。2023年陳尚林[6]利用長短期記憶網(wǎng)絡(luò)（LSTM）神經(jīng)網(wǎng)絡(luò)對比亞迪銷量進(jìn)行預(yù)測，在短期預(yù)測中取得了很好的效果，但處理長時間序列數(shù)據(jù)時可能存在梯度消失或梯度爆炸等問題。

本文在綜合分析現(xiàn)有研究的基礎(chǔ)上，提出了一種ARIMA和LSTM組合模型的算法。該算法旨在結(jié)合ARIMA模型在捕捉線性趨勢方面的優(yōu)勢和LSTM模型在處理非線性特征和時間依賴性方面的優(yōu)勢，以更準(zhǔn)確地預(yù)測新能源汽車未來一年的銷量。通過這種方法，本文期望能夠克服單一模型的局限性，提高銷量預(yù)測的準(zhǔn)確性。

2 模型與方法

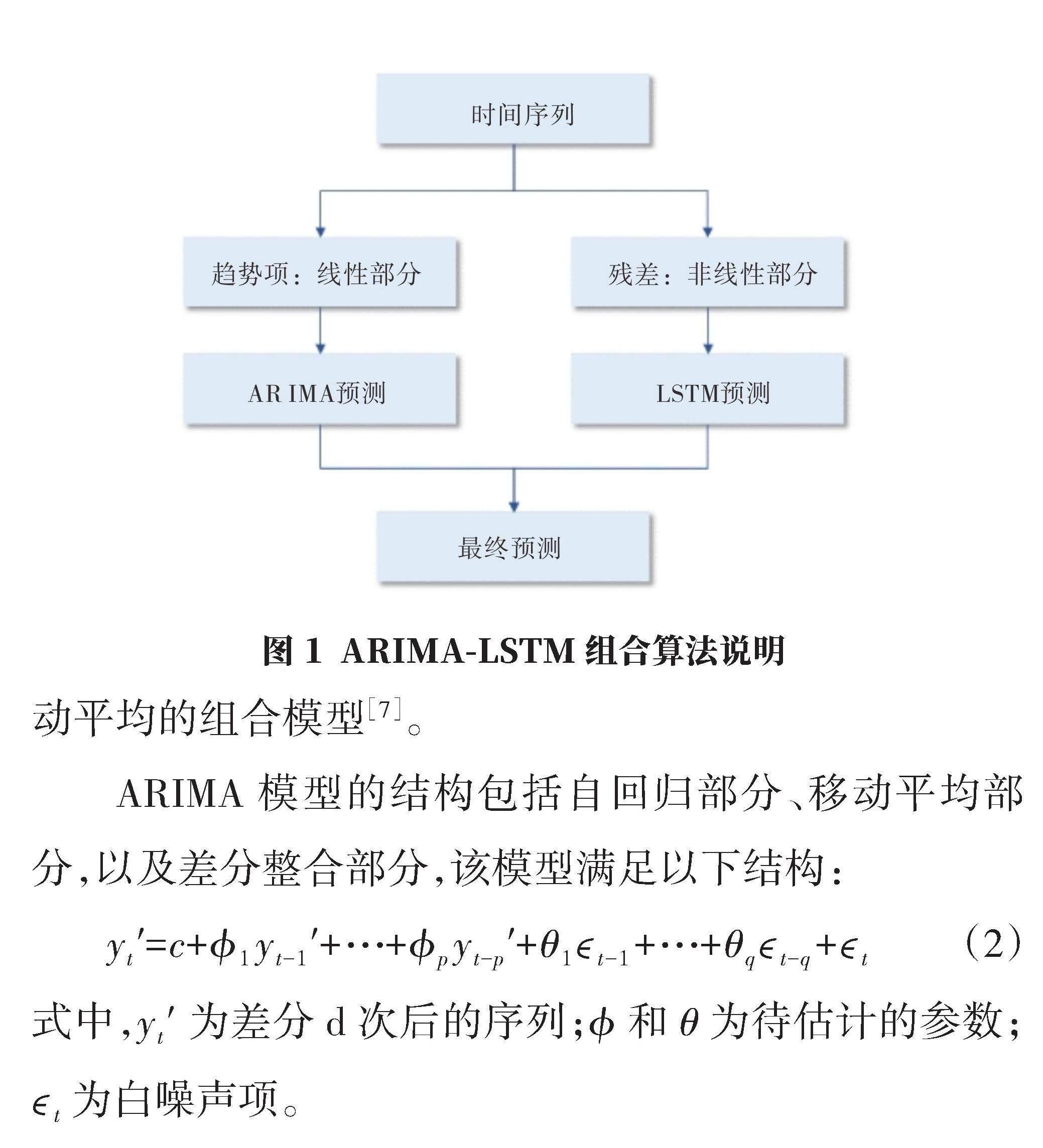
針對時間序列預(yù)測以及傳統(tǒng)神經(jīng)網(wǎng)絡(luò)預(yù)測模型的不足之處，本文提出了一種基于ARIMA和LSTM組合模型的算法，如圖1所示。該算法結(jié)合了ARIMA模型在時間序列線性趨勢預(yù)測方面的優(yōu)勢和LSTM模型在非線性特征捕捉方面的強大能力，使用ARIMA進(jìn)行趨勢項主體預(yù)測，使用LSTM對ARIMA回歸殘差進(jìn)行預(yù)測，充分利用了二者的優(yōu)勢，其模型如下：

[Yt=Yt，ARIMA+Yt，LSTM-residual]???????????????????? （1）

式中，[Yt]為組合模型在時間[t]的預(yù)測值，[Yt，ARIMA]為ARIMA模型在時間t的預(yù)測值，[Yt，LSTM-residual]為LSTM模型對時間[t]的殘差的預(yù)測值。

21 ARIMA部分

ARIMA（自回歸積分滑動平均模型）是一種強大的統(tǒng)計工具，專門用于分析非平穩(wěn)時間序列數(shù)據(jù)。該模型的核心在于，它首先通過差分技術(shù)將原始非平穩(wěn)序列轉(zhuǎn)換為平穩(wěn)序列，然后在這個平穩(wěn)序列上建立自回歸和移動平均的組合模型[7]。

ARIMA模型的結(jié)構(gòu)包括自回歸部分、移動平均部分，以及差分整合部分，該模型滿足以下結(jié)構(gòu)：

[yt'=c+?1yt?1'+…+?pyt?p'+θ1?t?1+…+θq?t?q+?t]???????? （2）

式中，[yt']為差分d次后的序列；[?]和[θ]為待估計的參數(shù)；[?t]為白噪聲項。

22 LSTM部分

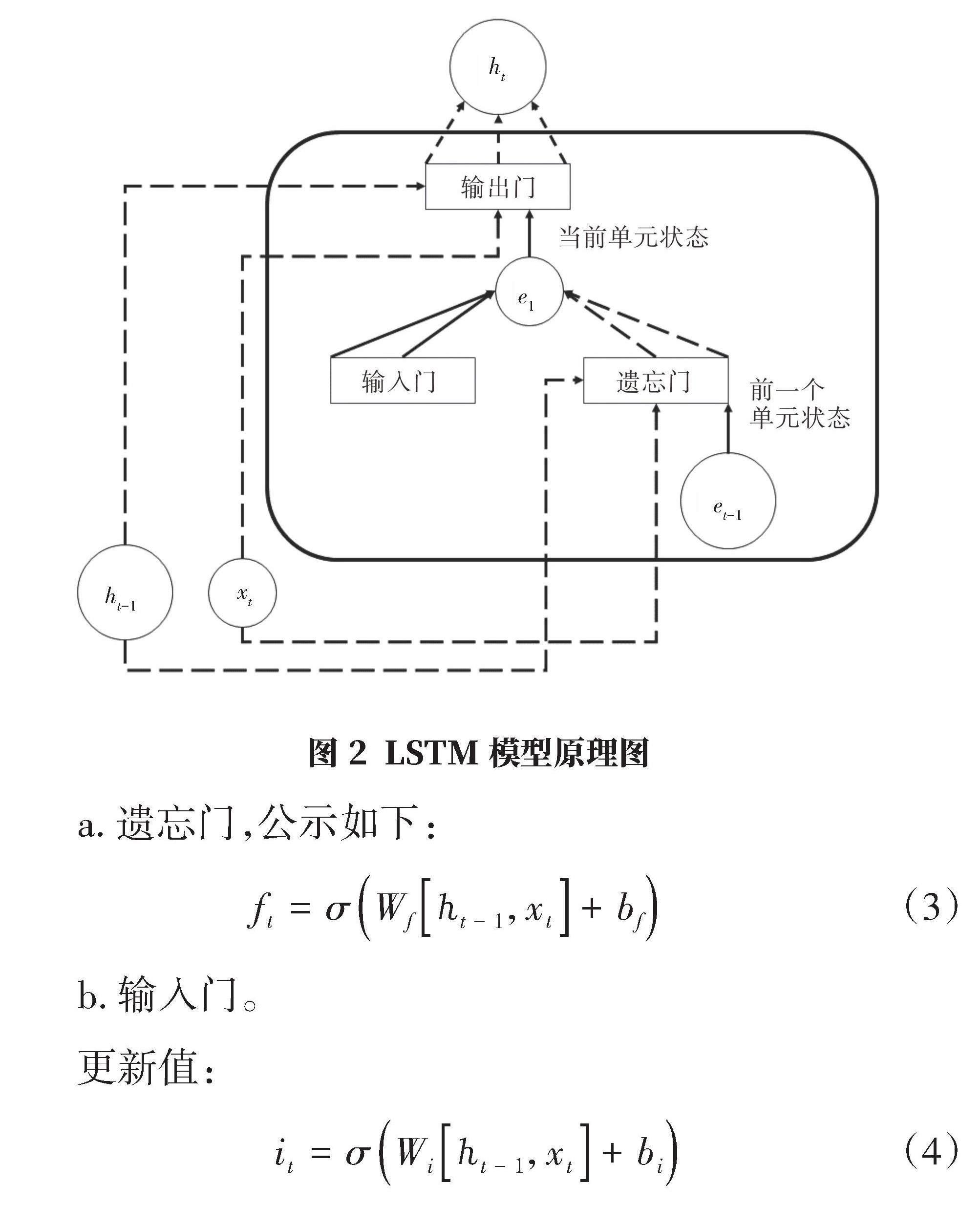
本文采用LSTM進(jìn)行非線性預(yù)測。LSTM模型的原理如圖2所示，它能夠捕捉到時間序列數(shù)據(jù)中的長期依賴關(guān)系，這一特性在銷量預(yù)測問題中至關(guān)重要。由于銷量數(shù)據(jù)常常受到過去事件的影響，LSTM模型能夠有效學(xué)習(xí)并應(yīng)用這種歷史信息來預(yù)測未來的銷售趨勢[8]。LSTM的核心是如何更新和計算細(xì)胞狀態(tài)[Ct]和隱狀態(tài)[?t]，下面給出具體公式。

[e1][ht][et-1][ht-1][xt]

a.遺忘門，公示如下：

[ft=σWf?t?1，xt+bf]??????????????????????? （3）

b.輸入門。

更新值：

[it=σWi?t?1，xt+bi]????????????????????? （4）

候選值：

[Ct=tanhWCht?1，xt+bC]??? ?????????????（5）

細(xì)胞狀態(tài)更新：

[Ct=tanhWC?t?1，xt+bC]?????????????? （6）

c.輸出門。

輸出值：

[ot=σWo?t?1，xt+bo]???????????????????????? （7）

隱狀態(tài)更新：

[?t=ottanhCt]????????????????????????????? （8）

3 實驗設(shè)計

31 數(shù)據(jù)獲取

華東地區(qū)作為中國經(jīng)濟的重要引擎，其新能源汽車市場發(fā)展迅速，消費者接受度高，且競爭態(tài)勢激烈。因此，選擇華東地區(qū)作為研究范圍具有代表性和實際意義。

在眾多新能源汽車品牌中，特斯拉與比亞迪憑借其卓越的技術(shù)實力、市場布局和品牌影響力，成為市場的領(lǐng)導(dǎo)者。特斯拉以其創(chuàng)新的電池技術(shù)、智能駕駛功能和獨特的營銷策略贏得了消費者的青睞；比亞迪則以其豐富的產(chǎn)品線、穩(wěn)定的性能和良好的性價比在市場上占據(jù)了一席之地。選擇這兩個品牌進(jìn)行研究，不僅有助于了解新能源汽車市場的發(fā)展趨勢，還能為其他品牌提供有益的參考和借鑒，因此本文選擇了華東地區(qū)特斯拉以及比亞迪電車的銷量數(shù)據(jù)進(jìn)行分析。

32 實驗步驟

本文將采用分別使用ARIMA、LSTM，以及兩者組合模型根據(jù)現(xiàn)有數(shù)據(jù)劃分訓(xùn)練集和測試集，比較組合模型和單一使用兩種模型時預(yù)測的RMSE。接著將對數(shù)據(jù)進(jìn)行處理，將原始數(shù)據(jù)隨機選取數(shù)據(jù)進(jìn)行調(diào)整，作為缺失值或異常值，再次進(jìn)行訓(xùn)練，模擬現(xiàn)實中可能存在的統(tǒng)計錯誤的情況。最后比較三個模型的靈敏度和魯棒性。

4 實驗結(jié)果分析

41 數(shù)據(jù)分析

首先對已有的數(shù)據(jù)進(jìn)行平穩(wěn)性檢驗，以便后續(xù)使用ARIMA。

在本次研究中，采用了單位根檢驗來對華東地區(qū)特斯拉與比亞迪兩個品牌的新能源汽車銷售數(shù)據(jù)進(jìn)行平穩(wěn)性檢驗，結(jié)果如表1所示。

由結(jié)果顯示，原始的新能源汽車銷售數(shù)據(jù)并不平穩(wěn)。因此采用一階差分進(jìn)行分析。一階差分是一種常用的時間序列數(shù)據(jù)平穩(wěn)化方法，它通過計算相鄰時間點的數(shù)據(jù)差值來消除數(shù)據(jù)中的趨勢和季節(jié)性波動。一階差分后，再次對數(shù)據(jù)進(jìn)行單位根檢驗，驗證其具有平穩(wěn)性。圖3所示為特斯拉華東地區(qū)銷量一階差分?jǐn)?shù)據(jù)。

a.比亞迪銷量一階差分后的數(shù)據(jù)

b.特斯拉銷量一階差分后的數(shù)據(jù)

由于差分階數(shù)越高會造成越多的數(shù)據(jù)特征損失，這里不在考慮更高階的差分。

42 預(yù)測性能

在ARIMA模型中，[p]和[q]分別代表自回歸項（AR）和移動平均項（MA）的階數(shù)。具體來說，[p]代表自回歸的階數(shù)，即要用到過去多少個時間點的數(shù)據(jù)來預(yù)測當(dāng)前時間點的值；[q]代表移動平均的階數(shù)，即要用到過去多少個白噪聲誤差項來預(yù)測當(dāng)前時間點的值。本文首先通過繪制一階差分?jǐn)?shù)據(jù)ACP圖和PACP圖來確定ARIMA模型中的[p、q]參數(shù)的值（圖4）。

對一階差分后的序列進(jìn)行自相關(guān)和偏相關(guān)判斷如圖4所示，從自相關(guān)圖和偏自相關(guān)圖可以看出，ACF和PACF均為一階截尾，因此可以確定模型中[p、q]的值均為1。因此，本文建立[ARIMA（1，1，1）]模型。

將已有的數(shù)據(jù)按照10∶1的比例劃分訓(xùn)練集和測試集，使用訓(xùn)練集訓(xùn)練模型并用測試集檢驗?zāi)Ｐ蜏?zhǔn)確性，最大迭代500次，模型在200次左右收斂，誤差達(dá)到穩(wěn)定。根據(jù)上述模型本文預(yù)測了未來一年兩種新能源汽車的銷量。

計算組合模型的RMSE與兩個單一模型分別預(yù)測時的RMSE，對比單一模型與組合模型預(yù)測性能，對比結(jié)果見表2。

可以看出，組合模型的預(yù)測效果明顯優(yōu)于單一模型的預(yù)測效果，預(yù)測的精度有明顯提升，能夠?qū)π履茉雌囦N量的趨勢進(jìn)行準(zhǔn)確的預(yù)測和跟蹤。相較于ARIMA和LSTM單一模型，組合模型具有更好的預(yù)測性能。

43 靈敏度檢驗

為了全面評估本文所采用的算法在處理實際數(shù)據(jù)中的缺失值和異常值時的穩(wěn)定性和魯棒性，本文進(jìn)行了靈敏度檢驗。本文隨機選擇了不同城市的數(shù)據(jù)，并針對每個城市隨機抽取了兩個月的數(shù)據(jù)進(jìn)行特殊處理：將其中一個月的數(shù)據(jù)設(shè)置為缺失值，以模擬實際數(shù)據(jù)中可能出現(xiàn)的缺失情況；而將另一個月的數(shù)據(jù)設(shè)置為異常值，以檢驗算法在面對極端或偏離常態(tài)的數(shù)據(jù)時的表現(xiàn)。

在數(shù)據(jù)預(yù)處理階段，本文采用了插值方法來補全缺失值。然后本文用三個模型分別進(jìn)行預(yù)測，并比較三種方法的RMSE，結(jié)果如表3所示。

通過表3可以看出，ARIMA-LSTM組合模型的RMSE明顯小于單獨使用兩個模型，因此可以看出組合模型有良好的穩(wěn)定性和魯棒性，可以很好地適應(yīng)實際情況。

5 結(jié)語

本文從新能源汽車的銷量出發(fā)，建立了ARIMA-LSTM組合模型，組合模型展現(xiàn)出了更優(yōu)異的預(yù)測性能。這一研究不僅提升了銷量預(yù)測的精度，也為企業(yè)的戰(zhàn)略決策提供了有力支持。

對于企業(yè)而言，通過精確的銷量預(yù)測能夠合理制定生產(chǎn)計劃、優(yōu)化庫存管理、降低運營成本，進(jìn)而提升市場競爭力。通過深入分析銷量背后的因素，企業(yè)可以更有針對性地調(diào)整產(chǎn)品策略和市場布局。本文的研究成果能夠為新能源汽車行業(yè)的發(fā)展提供有益的參考和啟示，并期待在未來的研究中繼續(xù)拓展和深化相關(guān)領(lǐng)域的探索。

參考文獻(xiàn)：

[1]廖榮洋，計春雷，任菊慧，等一種基于小波分析和ARIMA-LSTM的汽車銷量預(yù)測方法[P]中國專利：CN115564474A，2023-01-03.

[2]桂思思，孫偉，徐曉鋒基于ARIMA與線性回歸組合模型的汽車銷量預(yù)測分析[J]計算機與數(shù)字工程，2021，49（8）：1719-1723.

[3]陳科秀，劉娟基于ARIMA模型的歐拉黑貓新能源汽車銷量預(yù)測[J]現(xiàn)代工業(yè)經(jīng)濟和信息化，2022，12（3）：169-171.

[4]Agbessi A P，Salami A A，Agbosse K，et al.Peak Electrical Energy Consumption Prediction by ARIMA，LSTM，GRU，ARIMA-LSTM and ARIMA-GRU Approaches[J]Energies，2023，16（12）：4739.

[5]張怡基于ARIMA-LSTM混合模型的時間序列分析研究與應(yīng)用[D]荊州：長江大學(xué)，2023.

[6]陳尚林基于LSTM神經(jīng)網(wǎng)絡(luò)和百度指數(shù)的新能源汽車銷量預(yù)測——以比亞迪為例[D]武漢：湖北大學(xué)，2023.

[7]呼雄偉基于ARIMA-LSTM組合模型在鋼瓶銷量預(yù)測中的研究與應(yīng)用[D]上海：上海第二工業(yè)大學(xué)，2022.

[8]劉麗佳，李曉雪，王海濱，等考慮節(jié)假日的ARIMA模型在酸奶銷量預(yù)測中的應(yīng)用[J]計算機科學(xué)與應(yīng)用，2023（12）：2172-2179.

作者簡介：

張鈺妍，女，2003年生，本科在讀，研究方向為管理科學(xué)與工程。