機器人學基礎課程軌跡規劃仿真教學研究

李壯 方貞琪 王興宇 唐樂 陳章寶

【摘?? 要】?? 機器人軌跡規劃技術是機器人學基礎課程中的核心內容，是研究機器人、機械臂等系統的重要理論基礎，課程體現了較強的實踐性，理論知識涉及三維空間，公式推導過程較為復雜、抽象。應用MATLAB中強大的數值計算和可視化功能，結合軌跡規劃中理論公式對機器人軌跡進行規劃、分析。通過數值仿真對機器人笛卡爾空間、關節空間的軌跡進行規劃，讓學生直觀地學到軌跡規劃理論，掌握從公式推理到數值仿真的實踐過程，增強學生對軌跡規劃的理解，提高學生的專業知識能力，提升教學效果。

【關鍵詞】?? 軌跡規劃；MATLAB；關節空間；笛卡爾空間；數值仿真

Research on Simulation Teaching of Trajectory

Planning of Basic Course of Robotics

Li Zhuang， Fang Zhenqi， Wang Xingyu， Tang Le， Chen Zhangbao

（Bengbu College， Bengbu 233030， China）

【Abstract】??? Robot trajectory planning technology is the key chapter in the basic course of robotics， and it is an important theoretical basis for the research of robot for robot arm and other systems. The course embodies strong practicality， its theoretical knowledge involves three-dimensional space， the theory is relatively complex and abstract， the formula derivation process also is complex. The powerful numerical calculation and visualization functions in MATLAB are applied to plan and analyze the trajectory of the robot in combination with the theoretical formulas in trajectory planning. Through numerical simulation， the trajectory planning of robot cartesian space and joint space is carried out， so that students can intuitively learn the trajectory planning theory， master the practical process from formula reasoning to numerical simulation， enhance students' understanding of trajectory planning， improve their professional knowledge and ability， and enhance the teaching effect.

【Key words】???? trajectory planning; MATLAB; joint space; cartesian space; numerical simulation

〔中圖分類號〕 TP242.6????????????? ?????? ????? ???〔文獻標識碼〕? A????? ???????????? 〔文章編號〕 1674 - 3229（2024）02- 0107 - 07

[收稿日期]?? 2023-11-13

[基金項目]?? 安徽省高等學校省級質量工程項目“機器人工程新建專業質量提升項目” （2022xjzlts025）；校級教研項目“新工科背景下‘機器人學基礎課程教學與實踐能力培養探索與實踐”（2023jyxm16）；國家級大學生創新創業訓練計劃項目“疫情下一種只能送餐送藥機器人”（20221135007）

[作者簡介]?? 李壯（1994- ），男，碩士，蚌埠學院電子與電氣工程學院助教，研究方向：分布式模型預測控制、多智能體協同。

0???? 問題提出

機器人的軌跡規劃是機器人學基礎課程中重難點知識，也是機器人運動學的重要基礎理論，其對機器人控制起到重要作用。機器人的空間軌跡包括位置、速度以及加速度等基本物理量，其包括笛卡爾空間路徑規劃和關節空間路徑規劃［1-2］。機器人進行軌跡規劃的主要目的是在于已知機器人初、末狀態位置時，機器人如何實現從初始位置平穩地達到終點位置。軌跡規劃包括多種方式，在軌跡中存在奇異位置，靠近其位形時，關節速度會趨于無窮大，應避免此類情況出現；軌跡規劃過程中，位置、速度以及加速度等變量需要滿足基本約束條件和自由度參數，因此機器人的軌跡規劃過程就顯得十分重要［3-4］。

針對軌跡規劃問題，眾多學者開展了不同的研究。文獻［5］根據不同類型的軌跡規劃方法展開研究；文獻［6］針對工業機器人應用不同的軌跡方法進行設計仿真，總結相關特點；文獻［7］介紹了軌跡規劃中多項式插值方法和笛卡爾空間軌跡規劃方法，并針對能量、時間等參數進行研究分析、歸納。文獻［8］就如何提高實驗操作的可行性和課程教學提出了相關措施方法。

機器人學基礎課程中詳細闡述了笛卡爾空間規劃和關節空間規劃，其中關節空間規劃包括多項式路徑規劃、拋物線擬合線性插值路徑規劃等；笛卡爾空間路徑規劃包括空間直線位置插值、空間圓弧位置插值以及姿態插值等［9-10］。本文將對上述兩種方式進行理論分析、推導和數值仿真，最后對路徑規劃內容進行總結。

機器人工程專業涉及專業知識較多，尤其是數學計算與推導部分，成為了眾多學生的難題，單純的理論計算在一定程度上削弱了學生的實踐能力，進而影響到專業的發展［11］。本文就機器人學基礎課程建設問題在課程中融入實例仿真，同時結合工業機器人設備和視覺搬運機器人開展實踐操作與學習，進一步提升學生的專業素質能力和綜合實踐能力。

1???? 關節空間路徑規劃

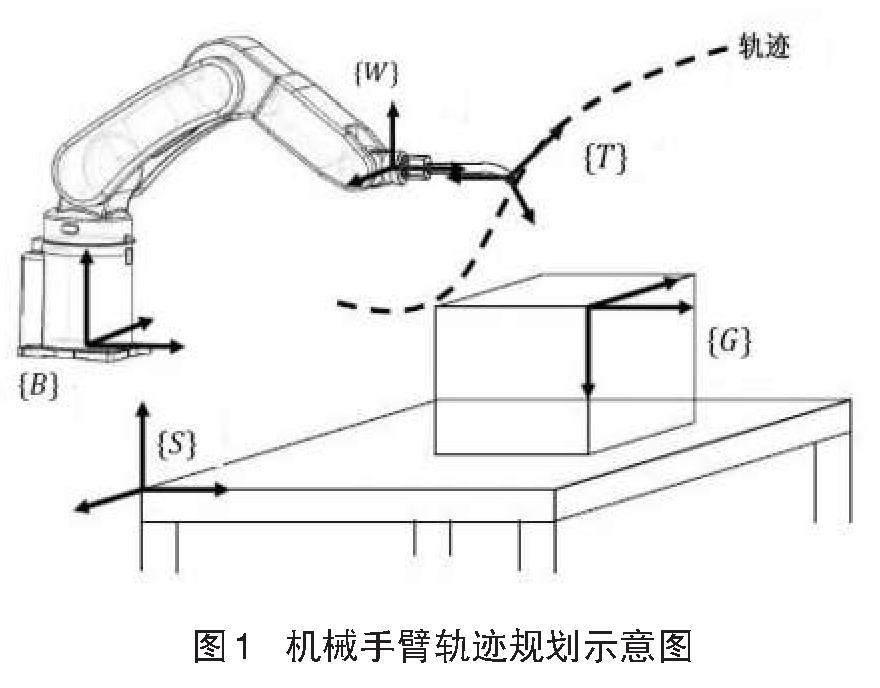
關節空間是對機器人的各個關節進行規劃，規劃參數有位置、角度等。關節空間規劃是以關節角度的函數來描述機器人的軌跡，不考慮工作空間坐標中的路徑形狀，計算較為簡單。圖1為機械手臂軌跡規劃圖。

其中虛線表示機械手臂末端的軌跡，B、S、W、T、G分別表示基坐標系、站坐標系、腕部坐標系、工具坐標系以及目標坐標系，根據坐標相對位置關系確立其次坐標變換矩陣，進行軌跡規劃。

在關節空間軌跡規劃中重點考慮初始點和目標點的位姿、速度以及加速度，其特點是計算量小、運行速度快等。軌跡規劃示意圖如圖2所示。

在關節空間下軌跡規劃基本步驟為：

（1）定義工具坐標系T相對目標坐標系G的初始位置、路徑點和終點，并根據變換方程依次求解各關節手臂的旋轉轉矩R。

（2）應用逆向運動學將手臂末端點狀態轉換到空間狀態。

（3）對所有節點進行規劃，并得到相應平滑曲線。

（4）應用正向動力學將關節狀態轉換到手臂末端點狀態，檢查末端點在笛卡爾坐標系下軌跡的可行性。

1.1?? 三次多項式

如果使機器人在一段軌跡上運行平穩，且路徑軌跡為平滑曲線，由于三次多項式的函數是連續的，則對應的關節速度和加速度也滿足連續性，在一定程度上避免了奇異位置。通常情況下，三次多項式包含4個約束條件，分別為機器人初始關節角度和終點關節角度，初、末速度為0，即滿足：

[θt0=θ0，θtf=θfθt0=0，θtf=0]????????????? （1）

因此選擇三次多項式為：

[θt=a0+a1t+a2t2+a3t3]????????? （2）

其中a0、a1、a2、a3為常數參數。

由公式（2）可知，在任意時刻，對其求解一階導數和二階導數，對應軌跡的速度和加速度分別為：

[θt=a1+2a2t+3a3t2θt=2a2+6a3t]??????????? （3）?????????????????????????????? 根據式（1）～式（3）可得

[θ0=a0θf=a0+a1tf+a2tf2+a3tf30=a10=a1+2a2tf+3a3tf2]????????? （4）

進而求出參數a0、a1、a2、a3，其分別為：

[a0=θ0a1=0a2=3t2fθf-θ0a3=-2t3fθf-θ0]?????????????? （5）

則三次多項式插值函數為

[θt=θ0+3t2fθf-θ0t2+3t2fθf-θ0t3]? （6）??????????????????? 結合理論推導和分析，應用MATLAB進行數值仿真，其結果如圖3所示。

由圖3可知，在建立關節函數后，已知起始、終點位姿后，可確立關節空軌跡插補曲線。

1.2??? 高次多項式

在路徑規劃過程中，當考慮約束條件較多時，則可以應用高階多項式作為路徑段進行規劃；如考慮約束條件包括路徑段的起始點和終點位置、速度以及加速度時，則可采用高階多項式插值函數進行軌跡規劃，其表達式為：

[θt=a0+a1t+a2t2+a3t3+a4t4+a5t5]? （7）?????????????????????? 其中a0、a1、a2、a3、a4、a5為常數參數；對式（7）分別求解多階導數：

[a0=θ0θf=a0+a1t+a2t2+a3t3+a4t4+a5t5θ0=a1θf=a1+2a2tf+3a3tf2+4a4tf3+5a5tf4θ0=2a2θf=2a2+6a3tf+12a4tf2+20a5tf3]? （8）???????????????????? 式（8）為軌跡規劃的約束條件。通過求解，高次多項式參數分別為：

[a0=θ0a1=θ0a2=θ02a3=20θf-20θ0-8θf+12θ0tf-3θ0-θft2f2t3fa4=30θf-30θ0+14θf+16θ0tf+3θ0-2θft2f2t4fa5=12θf-12θ0-6θf+6θ0tf-θ0-θft2f2t5f]?????????????? （9）

在MATLAB中添加Robotics Toobox中的tpoly函數，對上述內容進行仿真分析，結果如圖4所示。圖（a）為機器人關節移動位移，圖（b）為機器人關節速度變化，圖（c）為機器人關節加速度變化曲線。

由圖4可知，在考慮多約束條件時，機器人關節角度、角速度以及加速度變化滿足對應數值關系，軌跡規劃過程中未出現奇異位形。

2???? 笛卡爾空間軌跡規劃

在關節空間中進行軌跡規劃時，要使機械臂到達期望的位姿，但其無法保證末端執行器在笛卡爾空間中路徑的線性。因此對機器人操作器末端規劃要求精確時，則應當考慮笛卡爾空間路徑規劃。其規劃步驟為：

（1）定義工具坐標系T相對目標坐標系G的初始位置、路徑點和終點，應用各節點位置和旋轉列寫出各個節點位姿。

（2）對各位置點坐標選取曲線進行擬合，進而對手臂末端點狀態進行規劃。

（3）將規劃好的手臂末端點狀態的軌跡轉換到關節空間。

（4）檢查節點狀態在關節空間下的軌跡是否具備可行性。

2.1?? 直線軌跡規劃

直線軌跡規劃是指已知始末兩端位置和姿態時，求解軌跡中間點的姿態和位置，主要包括兩種方法，分別為對中間位置的分量進行直接插補和利用驅動函數進行插補。下面介紹對中間位置的分量進行直接插補。

在空間當中存在任意兩點，分別為起始時A（x0，y0，z0），終點B（xf，yf，zf），其中直線插補次數為N，插補點的位姿和位置可求得為：

[xi+1=xi+i+1Δxyi+1=yi+i+1Δyzi+1=zi+i+1Δz??? i=0，1，…，N]???? （10）

其中xi、yi、zi為插補點位置，[Δx]、[Δy]、[Δz]為位置增量，其解為：

[Δx=xf-x0N+1Δy=yf-y0N+1Δz=zf-z0N+1]??????????? （11）

由圖5、圖6可知，對機械臂末端執行器軌跡進行直線插補規劃，其路徑直觀，滿足線性關系，關節角度變化在對應范圍內。

2.2?? 圓弧軌跡規劃

通常圓弧軌跡規劃包括平面圓弧和空間圓弧，以平面圓弧軌跡規劃為例。在二維平面中存在任意一點，并作為圓心o，其半徑大小為r、圓心角為b、插補次數為N，在此圓弧上存在多個位置，可通過旋轉關系求解圓弧上點的坐標，考慮起始相角為g，其示意圖如圖7所示。

[xA=x0+rsinγyA=y0+rcosγzA=z0 ]??????????? （12）

由圖7可知，其位置關系滿足：

[xC=x0+rsinγ+βyC=y0+rcosγ+βzC=z0 ]?????? （13）

[Δβ=β/N+1]???????????? （14）

則圓弧上任意一點坐標pi（xi，yi，zi）為

[xi=x0+rsinγ+iΔβyi=y0+rcosγ+iΔβzi=z0??? i=0，1，2，…，N+1]??? （15）

根據上述公式推導和圓弧軌跡規劃原理，應用MATLAB進行數值仿真，其結果如圖8所示。

如圖8、圖9所示，應用圓弧插補方式進行軌跡規劃，插補值在圓弧上，末端執行器規劃過程中不會累積偏差，精確度高，位置變化曲線滿足相應關系。

3???? 應用案例

為了更好地展示機械臂末端執行器軌跡規劃過程，本案例應用實物機械臂設備一套，如圖10（a）所示，主要包括視覺設備一套、氣泵以及轉臺設備等。如圖11所示，首先獲取物件位置，即物件坐標系，并確立執行器末端坐標，包括其位置和姿態，進一步對機械臂4個關節進行控制，設置相應關節角。由圖12可知，機械臂在規劃好的軌跡上運動，可實時反饋關節位置和姿態。其過程示意圖分別如圖10（b）、10（c）、10（d）所示，機械臂末端執行器獲取目標點，并獲取物件，按照對應軌跡進行關節轉動，最后將物件放置目標位置，完成軌跡規劃和物件抓取的任務。圖13表示關節規劃參數的設置。

4???? 結語

本文通過理論推導和應用MATLAB數值仿真計算分析了關節空間規劃和笛卡爾空間規劃兩種方式，兩類規劃方法適用于不同情況。將課程知識與仿真實例相結合，并依托學院相關視覺機械臂開展實際的軌跡規劃操作，使得學生深刻理解專業知識，掌握軌跡規劃的概念與實際工程意義，培養學生問題分析能力和解決問題能力，進一步激發機器人工程專業學生學習的主觀能動性，同時提升了課堂效率和教學效果。

［參考文獻］

［1］ 皇甫小峰，鄒光明，劉源泂，等.基于分段插補的焊接軌跡規劃研究［J］.農業裝備與車輛工程，2023（3）：1-8

［2］ 盧凌霄，董乾鵬，張天樂，等.機器人運動學與運動規劃算法綜述［J］.印刷與數字媒體技術研究，2023（5）：1-16.

［3］ 胡凌燕，李建華，陳江南，等.機器人控制基礎與實踐教程［M］.北京：高等教育出版社，2022.

［4］ 張家琪，馬躍，張智濤，等.一種高速并聯機器人的運動學建模與軌跡規劃仿真［J］.機械設計，2023，40（9）：43-48.

［5］ 李尉，鄧朝暉，葛吉民，等.機器人關節空間軌跡規劃研究進展［J］.機械設計與制造工程，2022，51（10）：15-23.

［6］ 范祺，蔡玉強，賈思楠.多種方法的工業機器人軌跡規劃與仿真［J］.華北理工大學學報（自然科學版），2022，44（4）：60-67.

［7］ 郭萍.工業機器人軌跡規劃研究［J］.中國新技術新產品，2022（19）：42-45.

［8］ 楊金鐸，王林波，曾惜，等.自動化機器人軌跡跟蹤與路徑規劃技術研究［J］.自動化儀表，2022，43（7）：40-45.

［9］ 盧青，郭建國.“新工科”背景下的機器人軌跡規劃實驗教學系統設計［J］.實驗室研究與探索，2022，41（5）：147-150+201.

［10］ 董理，楊東，鹿建森.工業機器人軌跡規劃方法綜述［J］.控制工程，2022，29（12）：2365-2374.

［11］ 羅少軒，喬愛民，王艷春.工業機器人關節復合力測量實驗裝置設計及其教學應用［J］.廊坊師范學院學報（自然科學版），2023，23（2）：108-111.