強化過程教學,打造高效課堂
王雪濤
《義務教育數學課程標準(2022年版)》強調,要重視數學結果的形成過程,處理好過程與結果的關系。在教學實踐中,數學教師應特別關注推理、推導等關鍵環節,幫助學生在此過程中積累經驗,鍛煉數學思維能力。本文以人教版三年級上冊第七單元《長方形和正方形的周長》復習課為例,探索如何強化過程教學,打造高效的小學數學課堂。
從動手實踐走向類比思考
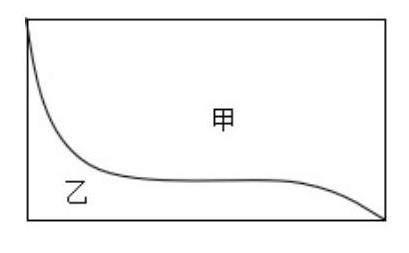
復習課的教學重點在于幫助學生鞏固所學內容,促進學生融會貫通地運用知識。為此,教師需發揮引導作用,將零散的知識點串聯成系統。課程伊始,筆者拿出一張長方形白紙,將其剪為甲、乙兩部分,并向學生提問:“哪一部分的周長更長?”不少學生因為混淆了周長和面積的定義,誤以為甲的周長更長。于是,筆者首先進行了概念上的澄清,而后引導學生使用細繩分別圍繞兩部分的邊緣,模擬量出各自的周長,并進行直觀比較,結果發現兩者的周長相等。
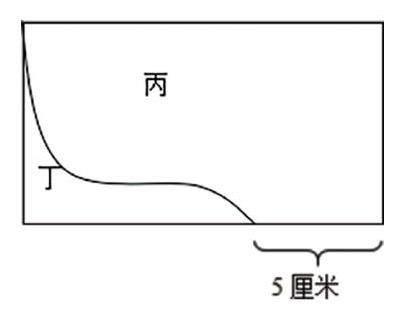
為了引導學生進一步思考周長的比較問題,筆者又拋出一個問題:“除了用繩子圍一圍的方法,你們還有其他途徑來比較它們的周長嗎?”很快就有學生提出了“抵消”的思路:將甲、乙兩個圖形的周長分為直線和曲線兩部分,曲線為公共邊,可以進行“抵消”;直線部分分別是長方形周長的一半,同樣可以進行“抵消”,因此甲、乙兩部分周長相等。接下來,筆者趁熱打鐵,向學生提問:“現在,我們有一張長20厘米、寬15厘米的長方形紙片,按照特定的方式剪開,得到了丙和丁兩部分。請你們運用‘抵消的方法,求出丙的周長比丁長多少厘米。”于是,學生首先識別出丙、丁兩部分的公共邊,而后計算出剩余部分的長度,很快得出丙的周長比丁多10厘米。
從復習已知走向探究未知
在小學階段,部分同類的數學概念、原理及規律往往相互關聯、本質相通。為了引導學生進一步探討長方形和正方形周長的本質特點,筆者再次拿出一張長20厘米,寬15厘米的長方形白紙,并從中剪去了一個邊長最大的正方形,隨后詢問學生:“余下的長方形周長是多少厘米?”經過簡單的計算,學生求得答案為(15+5)×2=40厘米。
接著,筆者又出示了一道新的題目:在一個長為20厘米的長方形里剪去一個最大的正方形,問余下長方形的周長是多少?這一次,長方形的寬是一個未知量,立刻引起了學生們的注意。面對這個新的挑戰,不少學生起初感到困惑,不知如何求解。在筆者的提示下,他們開始嘗試將長方形的寬設定為不同的數值,并進行計算,結果發現,無論長方形的寬設定為多少,余下長方形的周長始終為40厘米。帶著這個疑問,學生開始了進一步思考。有學生提出,余下長方形周長的一半剛好等于原長方形的長邊長度,因此,余下長方形的周長始終為40厘米。通過這個過程,學生們也認識到,要求取某個圖形的周長,并非一定要分別知道其中某條邊長的具體數值,在某些情況下,只要能夠理解這個圖形的特征本質,就能借助轉化而來的其他條件快速求解。
未來,筆者將不斷提升自己的專業素養,深入探索過程教學,為打造心中理想的小學數學課堂貢獻力量。

