“一題多變”在高中物理習題課中的應用

蒙小海

摘?要：在高中物理教學中，習題課是學生學習的重要環節之一，通過解題訓練可以幫助學生鞏固知識、培養解決問題的能力.文章探討了“一題多變”策略在高中物理習題課中的應用，幫助學生掌握和應用知識.

關鍵詞：高中物理；習題課；一題多變

中圖分類號：G632???文獻標識碼：A???文章編號：1008-0333（2024）15-0073-03

“一題多變”教學方法旨在引導學生在解決問題時靈活運用知識，培養其創新思維和解決問題的能力［1］.在高中物理習題課上，教師會通過改變題目中的條件或數據，引導學生從不同的角度思考問題［2］.這種方法不僅可以加深學生對知識的理解，還可以訓練他們靈活運用所學知識解決實際問題的能力.通過多樣化的

條件設置，學生可以更好地理解物理原理，并且在解決實際問題時能夠有所啟發.在高中物理教學中，“一題多變”策略有著廣泛的應用和積極的教育意義.

1 習題課中的“一題多變”

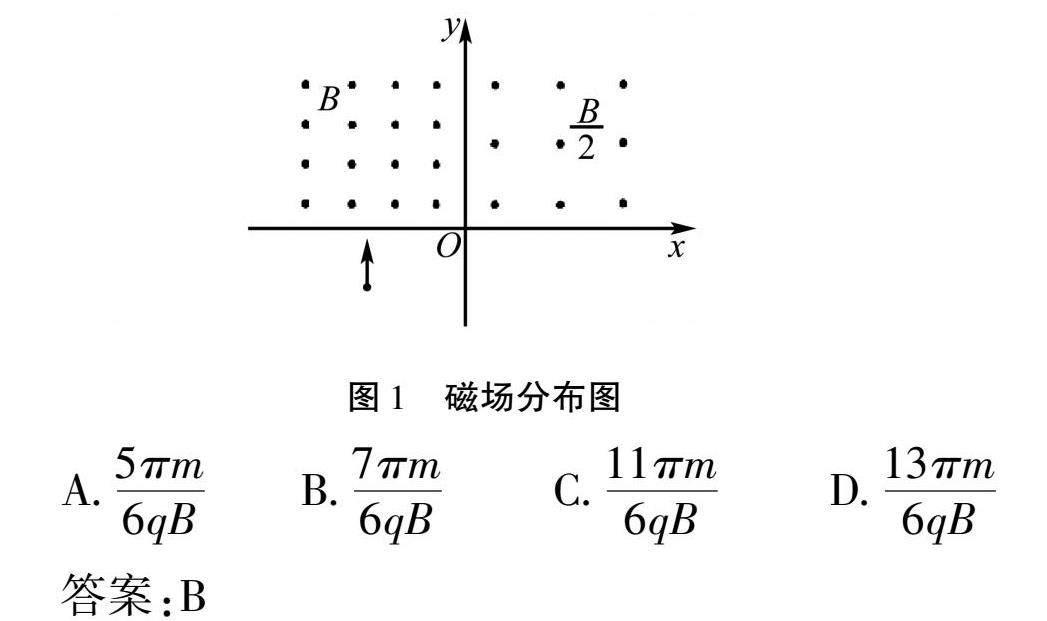
原題：如圖1所示，在一個平面直角坐標系內，存在著兩處大小不一、方向相同的勻強磁場.已知第一象限的磁感應強度大小為B/2，其方向垂直于紙面向外；第二象限內存在的磁場，磁感應強度大小為B.某時刻，從x軸負方向的某處，向磁場射入一個質量為m、電荷量為q（q>0）的粒子，該粒子進入磁場的方向和x軸垂直.該粒子的運動軌跡分為三個階段，階段一為垂直于x軸進入第二象限；階段二為以和y軸垂直的方向進入第一象限；第三階段為經過x軸，離開坐標系中的磁場.完成三階段，粒子一共經歷的運動時間為 ?（??）.

A.5πm6qB??B.7πm6qB ???C.11πm6qB?? ?????D.13πm6qB

答案：B

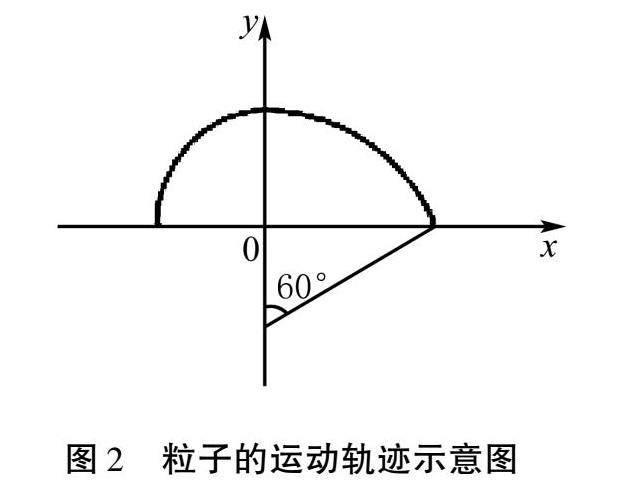
解析?粒子在磁場中的運動軌跡如圖2所示.

由示意圖可知，粒子在第二象限中轉動了90°，在第一象限中轉動了60°，即運動的第一部分是

14個周期，第二部分是16個周期.因此，粒子的運動時間為

t1=T24=14·2πmqB=πm2qB，t2=T16=16·

2πmq（B/2）=

2πm3qB

.則粒子在磁場中運動的時間為：t=t1+t2=

πm2qB+

2πm3qB=7πm6qB，因此B正確，ACD錯誤.答案為B.

變式1?以直線MN為界限，其左下方存在著一個無限大的勻強磁場，磁場垂直紙面向里，場強大小為B，示意圖如圖3所示.點P為一個粒子源，其位于勻強磁場中某處.從P點可以發射出速度方向不固定，但發射速率均為v＝3qBL2m的帶電粒子，已知帶電粒子的質量均為m，電荷量均為q，且粒子帶正電.直線MN上存在一點O，其和P點位于同一直線上，且PO=L，∠POM=60°，則粒子在磁場中運動的最短時間為（??）.

A.πm2qB??B.πm3qB??C.πm4qB??D.πm6qB

答案：B

解析?求解最短時間，核心在于找到帶電粒子運動的路徑.P點是一個粒子源，位于一個勻強磁場中，那么從P點發射出的帶電粒子將會受到磁場力作用，在磁場力的作用下做勻速圓周運動.根據洛倫茲力公式，此時有Bvq=mv2R，即：R=

mvBq=mBq·3BqL2m=32L;

粒子的運動周期為：T=2πRv=

3πL3BqL/2m=2πmBq；盡管粒子的初始速度方向不同，根據以上分析，粒子的運動半徑和運動的周期和速度并無關系，即周期和運動半徑一直保持不變.因此，當粒子在做圓周運動時，其轉過的圓心角越小，所對應的弦長也最小，運動時間即為最短.過P點作MN的垂線，根據幾何關系，可知，粒子運動軌跡的弦長最小為：Lsin

60°32LR，故最短弦長對應的圓心角為60°，所以，粒子在磁場中運動的最短時間為：tmin16Tπm3Bq，因此A、C、D選項錯誤，B選項正確.

變式2?如圖4所示，ab、bc、cd和da四個邊的邊長相等均為l，組成一個封閉的正方形.在該封閉的空間內，存在著一個大小為B的勻強磁場，磁場方向垂直所在的平面向外.O為ab邊的中點，該處放置有一個電子發射器，可以發射不同速率的電子，但所發射的電子均以垂直ab邊的方向進入該勻強磁場.已知發射的電子，比荷均為k.請分析當帶電粒子分別從a點和d點射出時，其速度分別為多少？

A.14kBl，54kBl???B.14kBl，54kBl

C.12kBl，54kBlD.12kBl，54kBl

答案：B

解析?根據幾何關系可知，由a點射出粒子半徑Ra=

l4=mvaBq，得va=Bql4m=Blk4，

由圖7可知，當粒子由d點射出時，此時的運動半徑為 ，R2=l2+（R-l2）2，R=54l，故vd=

5Bql4m=5klB4，因此B選項符合題意.

變式3?如圖5甲所示，三維坐標系中平面的右側存在平行z軸方向周期性變化的磁場B（未畫出）和沿y軸正方向豎直向上的勻強電場.將質量為m、電荷量為q的帶正電液滴從平面內的P點沿x軸正方向水平拋出，液滴第一次經過x軸時恰好經過O點，此時速度大小為v0，方向與x軸正方向的夾角為45°.已知電場強度大小E=mgq，從液滴通過O點開始計時，磁感應強度隨時間的變化關系如圖5乙示（當磁場方向沿z軸負方向時磁感應強度為正），t0=πv0g，重力加速度大小為g.求：

（1）拋出點P的坐標；

（2）液滴從第一次經過x軸到第二次經過x軸的時間；

（3）液滴第n次經過x軸時的x坐標；

答案：（1）（-v202g，v204g）；（2）mv02g；（3）2（n-1）v20g（n=1，2，3，…）

解析?（1）液滴做平拋運動，由于經過O點時方向與x軸正方向的夾角為，則vx=vy=v0sin45°=22v0.

根據平拋規律得（22v0）2=2gy1，22v0=gt1，x1=22v0t1.

聯立解得x1=-v202g，y1=v204g

P點的坐標為（-v202g，v204g）.

（2）由洛倫茲力提供向心力得qv0B1=mv20R1

聯立B1=mgqv0，解得R1=v20g

B1=mgqv0帶入周期公式T1=2πmqB1

解得T1=2πv0g=2t0

假設磁場不變，分析得液滴從第一次經過x軸到第二次經過x軸時，對應的圓心角為90°.則t1=T14=πv02g

假設成立.

（3）由于t1=T14=πv02g=t02

可知0～t0，液滴剛好轉過180°.之后磁場大小方向都變了，則偏轉方向變了.由洛倫茲力提供向心力得qv0B2=mv20R2

聯立B2=mg2qv0，解得R2=2v20g=2R1

B2=mg2qv0帶入周期公式

T2=2πmqB2

解得T2=4πv0g=4t0

t0～2t0，液滴轉過90°.

同理得，時間在2t0～3t0與0～t0的運動軌跡大小一樣，只是偏轉方向不一樣.

3t0～4t0與t0～2t0的運動軌跡大小一樣，只是偏轉方向不一樣.

綜上所述，得到液滴一個周期的軌跡圖如圖6.

由幾何關系得OA=AB=2R1

則液滴第n次經過x軸時的x坐標為

xn=（n-1）2R1=2（n-1）v20g（n=1，2，3，…）

2 結束語

在高中物理教學中，要想讓學生真正理解和應用物理規律，關鍵在于培養他們的物理思維.“一題多變”的教學方式，可以讓學生從多角度理解和應用物理規律，看透物理的本質.同時，讓學生反復訓練變式習題，鼓勵他們多思考、多比較，這樣可以幫助他們深入理解物理規律，掌握解題技巧.

參考文獻：

［1］戴建國.“一題多變”在高中物理習題課中的應用［J］.中學生數理化（學習研究），2016（04）：42-43.

［2］ 李勝強.“一題多變”在高中物理習題課中的應用［J］.實驗教學與儀器，2015，32（12）：8-10.

［責任編輯：李?璟］