無(wú)鋪裝層連續(xù)剛構(gòu)橋溫度梯度分析

朱廣 楊珊

摘要：為研究懸臂施工時(shí)無(wú)橋面鋪裝的連續(xù)剛構(gòu)橋豎向溫度梯度，文章依據(jù)實(shí)橋的溫度監(jiān)測(cè)數(shù)據(jù)，擬合了不同時(shí)期懸臂施工時(shí)的溫度梯度曲線，分析了溫度梯度作用在連續(xù)剛構(gòu)橋不同懸臂階段的影響，并基于溫度場(chǎng)實(shí)測(cè)數(shù)據(jù)，采用最小二乘法推導(dǎo)了PC連續(xù)剛構(gòu)橋主梁豎向溫度梯度曲線的擬合公式。結(jié)果表明：擬合曲線的計(jì)算值與實(shí)測(cè)值吻合良好，說(shuō)明了該溫度梯度曲線擬合公式精度很高，符合實(shí)際工程使用要求。

關(guān)鍵詞：連續(xù)剛構(gòu)橋；無(wú)鋪裝層溫度場(chǎng)；豎向溫度梯度；溫度監(jiān)控；最小二乘法

中圖分類號(hào)：U448.23? ?文獻(xiàn)標(biāo)識(shí)碼：A

文章編號(hào)：1673-4874（2024）04-0186-04

0 引言

受自然環(huán)境影響，主梁在其豎向方向上會(huì)產(chǎn)生一定的溫度梯度［1-3］，大跨度PC連續(xù)剛構(gòu)橋在懸臂施工時(shí)，在橋面主梁頂板處還沒(méi)有橋面鋪裝層，此時(shí)主梁頂板受到陽(yáng)光的直接照射，其表面溫度與箱梁內(nèi)的溫度會(huì)有很大的差別［4-5］。而《公路橋涵設(shè)計(jì)通用規(guī)范》（JTG D60-2015）中規(guī)定的溫度梯度曲線為有橋面鋪裝時(shí)的情況，因此實(shí)際的豎向溫度梯度曲線與規(guī)范中的溫度曲線有很大不同，造成相應(yīng)的溫度自內(nèi)力也與規(guī)范計(jì)算的有一定差異，最后導(dǎo)致按照《公路橋涵設(shè)計(jì)通用規(guī)范》（JTG D60-2015）計(jì)算得到的溫度梯度引起的主梁撓度值與實(shí)測(cè)值有偏差。

對(duì)于大跨度PC連續(xù)剛構(gòu)橋最大懸臂階段，上述計(jì)算偏差值造成的影響則更加明顯。因此，在懸臂塊段施工階段和合龍施工之前，需要對(duì)主梁的溫度進(jìn)行連續(xù)監(jiān)測(cè)，以測(cè)定實(shí)際主梁關(guān)鍵截面的實(shí)際溫度梯度曲線［6-7］，以此來(lái)準(zhǔn)確預(yù)估主梁懸臂在溫度梯度荷載作用下相應(yīng)的撓度變化值和精確控制主梁線形［8］。

本文以工程實(shí)例在懸臂施工期間的監(jiān)控實(shí)測(cè)數(shù)據(jù)為基礎(chǔ)，對(duì)工程實(shí)例不同施工階段的溫度場(chǎng)進(jìn)行分析與曲線擬合，將實(shí)測(cè)應(yīng)力與實(shí)測(cè)溫度梯度擬合曲線條件下的理論計(jì)算值和規(guī)范中的溫度梯度曲線條件下的理論計(jì)算值進(jìn)行對(duì)比分析。

1 項(xiàng)目概況及測(cè)點(diǎn)布置

1.1 項(xiàng)目概況

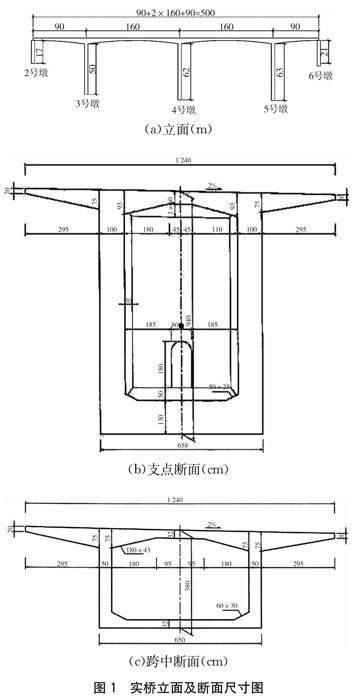
某連續(xù)剛構(gòu)橋的橋跨布置為（90+2×160+90）m，主橋上部結(jié)構(gòu)采用變截面單箱單室箱梁。單幅箱梁頂板寬12.4 m，底寬6.50 m，翼緣板懸臂長(zhǎng)2.95 m，懸臂端部厚20 cm，懸臂根部厚70 cm。支點(diǎn)處梁高9.4 m，為跨徑的1/17；跨中梁高3.8 m，為跨徑的1/42。如圖1所示。

1.2 溫度、應(yīng)力測(cè)點(diǎn)布置

考慮到縱橋向梁高的變化，在縱橋向方向上，選取主梁根部截面和主梁懸臂1/4截面這兩個(gè)具有代表性的截面作為溫度監(jiān)測(cè)的主要部位。同時(shí)，為了研究在實(shí)時(shí)溫度效應(yīng)影響下所選溫度截面的頂?shù)装鍛?yīng)力變化，在已選擇的溫度截面頂?shù)装宓纳舷戮壘荚O(shè)應(yīng)力傳感器，如下頁(yè)圖2所示。

1.2.1 截面溫度測(cè)點(diǎn)布置

受到不同角度陽(yáng)光照射時(shí)，箱梁不同部位的溫度會(huì)有較大差異，因此，箱梁橫截面上需布置足夠的溫度測(cè)點(diǎn)，來(lái)準(zhǔn)確測(cè)出實(shí)際的溫度場(chǎng)。箱梁溫度控制截面共布置25個(gè)溫度測(cè)點(diǎn)。根據(jù)國(guó)內(nèi)外溫度梯度的規(guī)定，頂板溫度梯度豎向范圍為40 cm，因此頂板豎向溫度測(cè)點(diǎn)布置在箱梁腹板處更為合適，Ⅰ3-Ⅰ8、Ⅰ9-Ⅰ14為頂板豎向溫度測(cè)點(diǎn)，間距為10 cm；箱梁頂板中部厚度為32 cm，Ⅰ15和Ⅰ16為頂板中部頂部與底部的溫度測(cè)點(diǎn)；Ⅰ17-Ⅰ22為腹板溫度測(cè)點(diǎn)；Ⅰ23-Ⅰ25為底板豎向溫度測(cè)點(diǎn)，位于底板頂部、中部和底部。最終溫度測(cè)點(diǎn)布置方式如圖3所示。

1.2.2 截面應(yīng)力測(cè)點(diǎn)布置

在溫度控制截面處布置相應(yīng)的應(yīng)力傳感器，在進(jìn)行溫度監(jiān)測(cè)的同時(shí)也對(duì)相應(yīng)截面關(guān)鍵部位的應(yīng)力進(jìn)行監(jiān)測(cè)，傳感器安裝在頂板最上層構(gòu)造鋼筋和底板最下層構(gòu)造鋼筋處［9］，截面應(yīng)力測(cè)點(diǎn)布置如圖4所示。

1.3 有限元模型

使用Midas Civil軟件建立全橋模型，全橋共52個(gè)施工階段，每個(gè)梁段均考慮掛籃移動(dòng)、混凝土澆筑、預(yù)應(yīng)力張拉三個(gè)施工過(guò)程。掛籃荷載重量為90 t，合龍吊籃重量為50 t，主梁與橋墩之間使用彈性連接中的剛性連接，橋墩底部使用一般支座，約束坐標(biāo)軸三個(gè)方向的位移與轉(zhuǎn)動(dòng)，有限元模型如圖5所示。

2 溫度場(chǎng)分析

主梁頂板一天中長(zhǎng)時(shí)間受到日照輻射，其溫度場(chǎng)在一天中會(huì)有明顯變化，使主梁產(chǎn)生較大的溫度應(yīng)力，是主梁溫度場(chǎng)分析中最為關(guān)鍵的一個(gè)部位，因此本文主要對(duì)主梁頂板部位的溫度場(chǎng)進(jìn)行分析。

2.1 高溫和低溫條件下施工的溫度監(jiān)測(cè)數(shù)據(jù)分析

《公路橋涵設(shè)計(jì)通用規(guī)范》（JTG D60-2015）并未對(duì)無(wú)橋面鋪裝的溫度梯度曲線進(jìn)行明確規(guī)定，但PC連續(xù)剛構(gòu)橋懸臂施工階段處于無(wú)鋪裝層狀態(tài)時(shí)更易受到環(huán)境溫度影響。在設(shè)計(jì)時(shí)出于保守考慮，一般按照最不利情況進(jìn)行驗(yàn)算，因此選取冬季低溫和夏季高溫條件下無(wú)鋪裝層溫度場(chǎng)監(jiān)控?cái)?shù)據(jù)進(jìn)行分析。

選取最有代表性的夏季及冬季24 h的頂板測(cè)點(diǎn)溫度監(jiān)控?cái)?shù)據(jù)繪制溫度變化曲線，下頁(yè)圖6為頂板橫向溫度場(chǎng)的監(jiān)控?cái)?shù)據(jù)曲線。分析可知，橫向溫度場(chǎng)測(cè)點(diǎn)數(shù)據(jù)在同一天中不同時(shí)刻的數(shù)值與溫度變化趨勢(shì)基本相同，同一時(shí)刻不同傳感器溫差均很小，其中冬季頂板最大橫向溫差值為1.2 ℃，夏季頂板最大橫向溫差值為3.5 ℃，說(shuō)明頂板橫向溫度梯度較小。而溫度數(shù)值及變化趨勢(shì)受日照及環(huán)境溫度影響較大，有明顯的峰值與谷值，日間12：00-14：00溫度達(dá)到夏季峰值50.5 ℃和冬季峰值15.5 ℃，在16：00日照消失后溫度迅速下降，在夜間04：00-06：00時(shí)溫度達(dá)到24 h內(nèi)的最小值。

下頁(yè)圖7為冬季及夏季豎向溫度場(chǎng)監(jiān)測(cè)數(shù)據(jù)曲線，其溫度變化同樣受日照影響較大，但不同于橫向溫度梯度，豎向溫度梯度分布較為明顯。在08：00之后，頂板位置溫度受日照影響溫度迅速上升，而靠近腹板內(nèi)側(cè)的測(cè)點(diǎn)溫度變化則相對(duì)平緩，14：00時(shí)，豎向溫差達(dá)到最大值，其中冬季與夏季最大豎向溫差分別為10.3 ℃和21.6 ℃。相較冬季豎向溫度場(chǎng)，夏季的環(huán)境溫度及日照更為劇烈，因此其頂板升溫速率更為明顯，最終豎向溫度溫差也更大。

因?yàn)樵O(shè)計(jì)中的溫差效應(yīng)一般以某時(shí)刻最大的溫度梯度作為控制溫度梯度，因此將監(jiān)控?cái)?shù)據(jù)中的最大溫度梯度與《公路橋涵設(shè)計(jì)通用規(guī)范》（JTG D60-2015）中規(guī)定的溫度梯度進(jìn)行對(duì)比，結(jié)果如圖8所示。受日照溫度場(chǎng)的影響，夏季與冬季的豎向溫差差異較大，而規(guī)范相較夏季溫度場(chǎng)及冬季溫度場(chǎng)的溫度梯度在數(shù)值上均相差較多，且在豎向溫度梯度的分布上也存在差異，監(jiān)控?cái)?shù)據(jù)的夏季豎向溫度梯度的影響深度約為500 mm，冬季豎向溫度梯度的影響深度約為300 mm，與規(guī)范中給出的400 mm影響深度差別較大。

在夏季和冬季中懸臂根部截面的應(yīng)力對(duì)比如表1所示，可以看出，底板應(yīng)力值由于自身數(shù)值很小，實(shí)測(cè)應(yīng)力值和規(guī)范計(jì)算值相差很小，但是頂板實(shí)測(cè)應(yīng)力值在懸臂根部處，冬季實(shí)測(cè)應(yīng)力值比理論應(yīng)力值小1.14 MPa，而夏季實(shí)測(cè)應(yīng)力值比理論應(yīng)力值大2.00 MPa。

由上述分析可知，監(jiān)控的豎向溫度梯度數(shù)據(jù)及相應(yīng)的應(yīng)力測(cè)點(diǎn)數(shù)據(jù)均與理論計(jì)算數(shù)值差異較大，且規(guī)范并未考慮季節(jié)及日照影響帶來(lái)的豎向溫度梯度變化。因此，需要考慮日照溫度場(chǎng)及無(wú)鋪裝層的影響，分別對(duì)夏季及冬季的豎向溫度梯度進(jìn)行修正。

3 溫度梯度曲線擬合的計(jì)算

3.1 溫度梯度曲線擬合

溫度梯度的時(shí)程曲線理論上是非線型曲線，形式上更加貼近《鐵路橋涵混凝土結(jié)構(gòu)設(shè)計(jì)規(guī)范》（TB10092-2017）中指數(shù)函數(shù)的形式，因此本文使用與該規(guī)范中類似的指數(shù)函數(shù)作為擬合曲線，擬合曲線公式如下：

Ty=T0e-ay（1）

式中：y——溫度計(jì)算點(diǎn)到頂板表面距離（m）；

T0——內(nèi)外溫度測(cè)點(diǎn)最大差值（℃）；

Ty——計(jì)算點(diǎn)處與距離頂板最遠(yuǎn)處計(jì)算點(diǎn)處的溫度差值（℃）；

a——實(shí)測(cè)日照溫差系數(shù)（m-1）。

根據(jù)式（1）可以看出，要得到主梁頂板的豎向溫度梯度曲線，只需要求出實(shí)測(cè)計(jì)算得到的日照溫差系數(shù)a即可。可以使用最小二乘法對(duì)參數(shù)a進(jìn)行求解。

給式（1）兩邊取對(duì)數(shù)得：

lnTy=-ay+lnT0（2）

令lnTy=t，lnT0=b，則：

t=-ay+b（3）

設(shè)測(cè)量數(shù)據(jù)一共是n組，則ti=lnTyi，令這組數(shù)據(jù)的平均值為t-，則數(shù)據(jù)的誤差平方和為：

δ=∑ni=1ti-t-2（4）

根據(jù)最小二乘法，使ti的誤差的平方和δ最小，可對(duì)δ中的a求導(dǎo)，并令其等于0，則：

dδda=2a2∑ni=1yi-2nab-t-=0（5）

解得：

a=nb-t-∑ni=1yi（6）

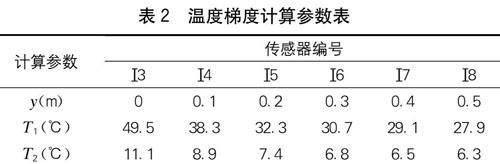
結(jié)合圖8中的數(shù)據(jù)和式（6），將計(jì)算需要的數(shù)據(jù)填于表2，其中夏季溫度為T1，冬季溫度為T2。

由表2數(shù)據(jù)計(jì)算得到夏季的頂板豎向溫度梯度擬合式為：

Ty=21.6e-7.25y（7）

冬季的頂板豎向溫度梯度擬合式為：

Ty=4.8e-7.53y（8）

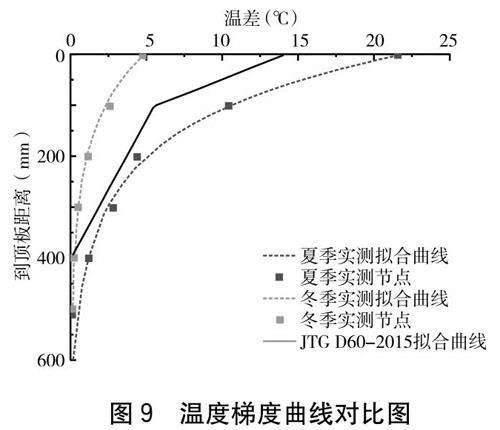
則頂板豎向的溫度梯度擬合曲線和《公路橋涵設(shè)計(jì)通用規(guī)范》（JTG D60-2015）的溫度梯度曲線對(duì)比如圖9所示。

由圖9可知，擬合曲線的擬合效果較好，能平順地穿過(guò)各個(gè)實(shí)測(cè)節(jié)點(diǎn)，證明了溫度梯度擬合公式的有效性。

3.2 曲線擬合結(jié)果與分析

將實(shí)測(cè)值擬合曲線的溫度梯度模式代入工程實(shí)例有限元模型中進(jìn)行計(jì)算，并將有限元計(jì)算結(jié)果與實(shí)測(cè)值進(jìn)行對(duì)比，這里僅計(jì)算升溫梯度下的模型情況。

懸臂根部截面應(yīng)力的理論值和實(shí)測(cè)值對(duì)比見(jiàn)表3，懸臂端部撓度變化的理論值和實(shí)測(cè)值對(duì)比見(jiàn)表4。

結(jié)合表3和表4可知，擬合曲線計(jì)算得到的應(yīng)力與撓度變化值與實(shí)測(cè)數(shù)據(jù)非常接近，在懸臂根部截面，冬季與夏季的擬合曲線計(jì)算得到的頂板應(yīng)力與實(shí)測(cè)值的差值分別為0.11 MPa和0.13 MPa；在懸臂端部截面，冬季與夏季的擬合曲線計(jì)算得到的撓度差值分別為0.16 mm和0.41 mm。

頂板處的應(yīng)力理論計(jì)算值與實(shí)測(cè)值偏差在4%以內(nèi)，而底板處由于自身應(yīng)力值較小，計(jì)算值與實(shí)測(cè)值的偏差在數(shù)值上與頂板相比也相對(duì)更小，可以看出，擬合曲線的計(jì)算結(jié)果與實(shí)測(cè)數(shù)據(jù)吻合良好。

4 結(jié)語(yǔ)

本文主要依據(jù)實(shí)橋的溫度監(jiān)測(cè)實(shí)測(cè)數(shù)據(jù)，分析了連續(xù)剛構(gòu)橋無(wú)鋪裝層不同時(shí)期的豎向溫度監(jiān)控?cái)?shù)據(jù)，并擬合了相應(yīng)環(huán)境溫度下的溫度梯度曲線，得出結(jié)論如下：

（1）連續(xù)剛構(gòu)橋無(wú)鋪裝層溫度場(chǎng)更易受到日照及環(huán)境溫度的影響，在懸臂施工階段需對(duì)主梁溫度場(chǎng)進(jìn)行監(jiān)測(cè)，以準(zhǔn)確掌握溫度變化對(duì)主梁產(chǎn)生的相應(yīng)影響，保證主梁線形平順與后期合龍施工的順利進(jìn)行。

（2）基于溫度場(chǎng)實(shí)測(cè)數(shù)據(jù)，采用最小二乘法推導(dǎo)了豎向溫度梯度曲線擬合公式，并將擬合結(jié)果與實(shí)測(cè)數(shù)據(jù)進(jìn)行對(duì)比。計(jì)算得到的懸臂關(guān)鍵截面應(yīng)力變化值與懸臂端部撓度變化值與監(jiān)控實(shí)測(cè)值的誤差較小，驗(yàn)證了本文豎向溫度梯度擬合曲線的有效性，符合實(shí)際工程要求。

參考文獻(xiàn)

［1］趙人達(dá)，王永寶.日照作用下混凝土箱梁溫度場(chǎng)邊界條件研究［J］.中國(guó)公路學(xué)報(bào)，2016，29（155）：56-65.

［2］顧 穎，李亞?wèn)|，姚昌榮.太陽(yáng)輻射下混凝土箱梁溫度場(chǎng)研究［D］.公路交通科技，2016，33（2）：46-53.

［3］葉見(jiàn)曙，賈 琳，錢培舒.混凝土箱梁溫度分布觀測(cè)與研究［J］.東南大學(xué)學(xué)報(bào)（自然科學(xué)版），2002，32（5）：788-793.

［4］方 志，汪 劍.大跨預(yù)應(yīng)力混凝土連續(xù)箱梁橋日照溫差效應(yīng)［J］.中國(guó)公路學(xué)報(bào)，2007，20（1）：62-67.

［5］Hedegaard BD，F(xiàn)rench CEW，Shield CK.Investigation of thermal gradient effects in the i-35w st.Anthony Falls bridge［J］.Journal of Bridge Engineering，2013（18）：890-900.

［6］C H P.Temperature study of an experimental segmental concrete bridge［J］.Journal of the Prestressed Concrete Institute，1983（2）：78-97.

［7］宋一凡，劉來(lái)君，賀拴海.大跨徑橋梁施工控制溫度應(yīng)力分析［J］.中國(guó)公路學(xué)報(bào)，2004（1）：57-60.

［8］Brock D H，Catherine E W F，Carol K S.Investigation of Thermal Gradient Effects in the I-35W St.Anthony Falls Bridge［J］.Journal of Bridge Engineering，2013，18（9）：890-900.

［9］蔣贛猷，周 群，陳光輝.大跨PC連續(xù)剛構(gòu)橋主梁溫度梯度下的應(yīng)力分析［J］.中外公路，2019，39（3）：143-147.

作者簡(jiǎn)介：朱 廣（1990—），工程師，主要從事橋梁結(jié)構(gòu)設(shè)計(jì)與研究工作。

朱 廣（1990—），男，廣西北流人，工程師，碩士研究生，主要從事橋梁結(jié)構(gòu)設(shè)計(jì)與研究工作。