基于博弈論和BP神經(jīng)網(wǎng)絡(luò)的橋梁風(fēng)險(xiǎn)預(yù)測(cè)模型

黃偉 袁光杰

摘要：文章以橋梁施工風(fēng)險(xiǎn)的定義為主線，分析了常用橋梁風(fēng)險(xiǎn)評(píng)估方法的特點(diǎn)并取其長(zhǎng)處，同時(shí)引入了熵理論和博弈論思想，提出了一種新的風(fēng)險(xiǎn)評(píng)估方法——基于博弈論和BP神經(jīng)網(wǎng)絡(luò)的風(fēng)險(xiǎn)預(yù)測(cè)模型，并以龐納子大橋?yàn)楣こ虒?shí)例進(jìn)行應(yīng)用分析。研究可知：該模型以減少主觀成分為原則，通過提高評(píng)價(jià)指標(biāo)的準(zhǔn)確度、全面性和科學(xué)性進(jìn)而獲得可靠的風(fēng)險(xiǎn)預(yù)測(cè)值；該橋高墩施工風(fēng)險(xiǎn)值為0.348，判定該項(xiàng)目風(fēng)險(xiǎn)較低，在可接受范圍內(nèi)；主要風(fēng)險(xiǎn)因素依次為墩身垂直度、風(fēng)荷載、日照溫差、混凝土強(qiáng)度等；建議在施工過程中對(duì)其墩身垂直度進(jìn)行風(fēng)險(xiǎn)監(jiān)控。

關(guān)鍵詞：橋梁風(fēng)險(xiǎn)；博弈論；BP神經(jīng)網(wǎng)絡(luò)；風(fēng)險(xiǎn)評(píng)估方法；風(fēng)險(xiǎn)預(yù)測(cè)

中圖分類號(hào)：U442.3+9? 文獻(xiàn)標(biāo)識(shí)碼：A

文章編號(hào)：1673-4874（2024）04-0173-04

0 引言

隨著內(nèi)陸平原地區(qū)交通網(wǎng)日趨完善，公路橋梁建設(shè)的重心逐步向西部山區(qū)延伸［1］。這些橋梁往往處于風(fēng)力大、溫濕差大等復(fù)雜環(huán)境，施工過程面臨的風(fēng)險(xiǎn)較大，如何識(shí)別和應(yīng)對(duì)施工過程中可能發(fā)生的風(fēng)險(xiǎn)問題顯得愈加突出。通過風(fēng)險(xiǎn)評(píng)估來解決前述問題成為近年來的一個(gè)新思路。

然而，國(guó)內(nèi)外學(xué)者關(guān)于橋梁風(fēng)險(xiǎn)分析理論的研究和應(yīng)用相對(duì)較少，現(xiàn)有常用風(fēng)險(xiǎn)評(píng)估方法也存在一定的不足。因此，本文以橋梁施工風(fēng)險(xiǎn)的定義為主線，分析常用橋梁風(fēng)險(xiǎn)評(píng)估方法的特點(diǎn)并取其長(zhǎng)處，同時(shí)引入了熵理論和博弈論思想，提出一種新的風(fēng)險(xiǎn)預(yù)測(cè)模型，并以龐納子大橋?yàn)楣こ虒?shí)例進(jìn)行應(yīng)用，為指導(dǎo)工程風(fēng)險(xiǎn)評(píng)價(jià)提供高效準(zhǔn)確的方法。

1 橋梁施工風(fēng)險(xiǎn)的定義及度量

在橋梁施工過程中，對(duì)相關(guān)利益團(tuán)體的某種既定目標(biāo)造成影響的不確定事態(tài)［2］，稱為橋梁施工的風(fēng)險(xiǎn)事態(tài)，簡(jiǎn)稱橋梁施工風(fēng)險(xiǎn)。其一般的數(shù)學(xué)表達(dá)如式（1）所示，即風(fēng)險(xiǎn)值R是關(guān)于風(fēng)險(xiǎn)事件發(fā)生的概率p、風(fēng)險(xiǎn)后果c、目標(biāo)利益發(fā)生的概率q和目標(biāo)利益b的某種函數(shù)關(guān)系式，該式也呈現(xiàn)了風(fēng)險(xiǎn)與收益之間的博弈關(guān)系：

R=f（p，c，q，b）（1）

式中：R——風(fēng)險(xiǎn)的數(shù)值度量；

p——風(fēng)險(xiǎn)事件發(fā)生的概率；

c——風(fēng)險(xiǎn)事件引起的后果（損失）；

q——目標(biāo)利益發(fā)生的概率；

b——目標(biāo)利益。

其中，在并協(xié)原理下，風(fēng)險(xiǎn)事件發(fā)生的概率p與目標(biāo)利益發(fā)生的概率q呈互補(bǔ)關(guān)系，見式（2）；當(dāng)收益可忽略或難以衡量時(shí)［3］，可將式（1）簡(jiǎn)化為如式（3）所示，即由風(fēng)險(xiǎn)事件發(fā)生的概率p和風(fēng)險(xiǎn)后果c來綜合表達(dá)風(fēng)險(xiǎn)值R。

p+q=1（2）

R=f（p，c）（3）

2 常用橋梁風(fēng)險(xiǎn)評(píng)估方法分析

常用的橋梁風(fēng)險(xiǎn)評(píng)估方法有層次分析法、模糊綜合評(píng)價(jià)法、BP神經(jīng)網(wǎng)絡(luò)分析法。

2.1 層次分析法

層次分析法（AHP）是將與決策相關(guān)的因素分解為目標(biāo)、準(zhǔn)則、指標(biāo)等層次，對(duì)復(fù)雜決策問題的本質(zhì)、影響因素及其內(nèi)在關(guān)系等進(jìn)行深入分析，利用較少的定量信息使決策的思維過程數(shù)學(xué)化，從而為復(fù)雜問題提供簡(jiǎn)便的決策方法，適用于決策結(jié)果難以量化的場(chǎng)合。由層次分析法可計(jì)算風(fēng)險(xiǎn)因素的相對(duì)權(quán)重或發(fā)生概率，見式（4），但定量數(shù)據(jù)較少，定性成分多，其計(jì)算結(jié)果不易令人信服。

ω=f（p）f（p，c）（4）

2.2 模糊綜合評(píng)價(jià)法

模糊綜合評(píng)價(jià)法基于模糊數(shù)學(xué)將定性評(píng)價(jià)轉(zhuǎn)化為定量評(píng)價(jià)，適用于各種非確定性問題的解決。由模糊綜合評(píng)價(jià)法可計(jì)算風(fēng)險(xiǎn)值，見式（5）、式（6），但評(píng)價(jià)指標(biāo)權(quán)重向量ω的初始判斷矩陣、評(píng)價(jià)指標(biāo)關(guān)系矩陣S的構(gòu)建很大程度上受決策者主觀意向的影響，雙重主觀判斷使得評(píng)價(jià)結(jié)果向量B和風(fēng)險(xiǎn)值R的準(zhǔn)確性有待商榷。

B=ω·S（5）

R=B～·MT（6）

式中：B——評(píng)價(jià)結(jié)果向量；

ω——評(píng)價(jià)指標(biāo)權(quán)重向量；

S——評(píng)價(jià)指標(biāo)關(guān)系矩陣；

B～——?dú)w一化后的評(píng)價(jià)結(jié)果向量；

MT——評(píng)價(jià)等級(jí)的風(fēng)險(xiǎn)值向量。

2.3 BP神經(jīng)網(wǎng)絡(luò)分析法

BP神經(jīng)網(wǎng)絡(luò)是指一種基于逆?zhèn)鞑ニ惴ǖ亩鄬忧梆伨W(wǎng)絡(luò)，其本質(zhì)為一個(gè)輸入向量x[DD（-*9]→[DD）]到輸出向量y[DD（-*9]→[DD）]的函數(shù)，（見式7）［4］。BP網(wǎng)絡(luò)以自學(xué)習(xí)、自適應(yīng)、非線性映射等優(yōu)點(diǎn)在函數(shù)逼近等領(lǐng)域應(yīng)用甚廣，其在運(yùn)用中常與層次分析法相結(jié)合，將由層次分析法解得的各風(fēng)險(xiǎn)指標(biāo)權(quán)重作為網(wǎng)絡(luò)中目標(biāo)項(xiàng)目的變量，同時(shí)使自變量涵蓋了層次分析法準(zhǔn)確度不高的特性，進(jìn)而影響了網(wǎng)絡(luò)的預(yù)測(cè)值。

y→=f（x→）（7）

3 基于博弈論和BP神經(jīng)網(wǎng)絡(luò)的風(fēng)險(xiǎn)預(yù)測(cè)模型

基于上述對(duì)常用橋梁風(fēng)險(xiǎn)評(píng)估方法的分析，引入熵理論和博弈論思想，提出一種新的風(fēng)險(xiǎn)預(yù)測(cè)模型。

3.1 熵權(quán)法

在信息論中，熵為系統(tǒng)無序程度的度量。

熵權(quán)法是基于工程項(xiàng)目歷史或現(xiàn)有客觀數(shù)據(jù)的考察利用，有較強(qiáng)的數(shù)理依據(jù)，其基本思路是根據(jù)指標(biāo)的變異程度來確定客觀權(quán)重。對(duì)于某項(xiàng)指標(biāo)，其信息熵值越小，表明該指標(biāo)的離散程度越大，在綜合評(píng)價(jià)的權(quán)重越大，反之則相反。若某項(xiàng)指標(biāo)的值均相等，則該指標(biāo)在綜合評(píng)價(jià)中不起作用。因此，熵權(quán)本身并不表示指標(biāo)權(quán)重，而表示在該指標(biāo)下對(duì)評(píng)價(jià)對(duì)象的區(qū)分度。

3.2 博弈論集化模型

博弈論集化模型的核心思想是在不同賦權(quán)方法所獲取的指標(biāo)權(quán)重之間尋求一致或妥協(xié)，極小化可能的權(quán)重與各基本權(quán)重之間的偏差［5］，提高指標(biāo)賦權(quán)的科學(xué)性。具體實(shí)現(xiàn)過程如下：

運(yùn)用AHP、熵權(quán)法對(duì)評(píng)價(jià)指標(biāo)進(jìn)行求解，可得指標(biāo)權(quán)重集如式（8）所示，記基本權(quán)重向量ωl的任意線性組合如式（9）所示。運(yùn)用博弈論集化模型在前述兩種不同權(quán)重之間進(jìn)行優(yōu)化，由優(yōu)化目標(biāo)（ω與ωl的離差極小化）可推導(dǎo)出決策模型如式（10）所示。

ωl=（ωl1，ωl2，…，ωln） l=1，2（8）

ω=∑2l=1αlωl（9）

式中：αl——線性組合系數(shù)。

min‖∑2i=1αiωTi-ωTl‖（10）

根據(jù)矩陣的微分性質(zhì)，上述決策模型的最優(yōu)化一階導(dǎo)數(shù)條件［6］如式（11）所示，對(duì)應(yīng)式（12）的線性方程組。

∑i=1αiωlωTi=ωlωTl（11）

ω1·ωT1ω1·ωT2ω2·ωT1ω2·ωT2α1α=ω1·ωT1ω2·ωT2（12）

解式（11）并按式（13）進(jìn)行歸一化處理，最終可求得綜合指標(biāo)權(quán)重如式（14）所示。

αl=αl∑2l=1αl（13）

ω=∑2l=1αlωl（14）

3.3 基于博弈論和BP神經(jīng)網(wǎng)絡(luò)的風(fēng)險(xiǎn)預(yù)測(cè)模型

在定性定量綜合風(fēng)險(xiǎn)評(píng)估中，指標(biāo)權(quán)重的確定尤為重要。

為得到更準(zhǔn)確、更全面的工程指標(biāo)權(quán)重，以減少主觀成分為原則，在僅考慮“風(fēng)險(xiǎn)事件發(fā)生的概率p”這一判斷準(zhǔn)則下，立足于博弈論并以Nash均衡為協(xié)調(diào)目標(biāo)［5］對(duì)AHP權(quán)重、熵權(quán)進(jìn)行優(yōu)化，可根據(jù)實(shí)際相似工程評(píng)價(jià)指標(biāo)的變異程度，通過熵權(quán)對(duì)AHP指標(biāo)權(quán)重進(jìn)行修正，提高指標(biāo)的準(zhǔn)確度；同時(shí)，避免了單一賦權(quán)方法的片面性，獲得兼顧專家意見和項(xiàng)目客觀情況的綜合權(quán)重，提高了指標(biāo)的全面性、科學(xué)性。

聯(lián)合BP神經(jīng)網(wǎng)絡(luò)能學(xué)習(xí)和存貯大量類似項(xiàng)目輸入-輸出（風(fēng)險(xiǎn)事件發(fā)生的概率p-風(fēng)險(xiǎn)值R）模式映射關(guān)系的特性，合理有效地解決了非正態(tài)分布、非線性的風(fēng)險(xiǎn)預(yù)測(cè)問題［7］。

基于博弈論和BP神經(jīng)網(wǎng)絡(luò)的風(fēng)險(xiǎn)預(yù)測(cè)模型技術(shù)路線如圖1所示。該模型適用于決策系統(tǒng)難以定量的情形。

4 工程應(yīng)用

4.1 工程概況

G580線和田至康西瓦公路工程龐納子大橋位于新疆和田地區(qū)，主橋橋跨布置為100 m+100 m的預(yù)應(yīng)力混凝土連續(xù)剛構(gòu)橋（下頁圖2），T構(gòu)采用懸臂施工，最大懸臂長(zhǎng)度為93 m，橋?qū)? m，主墩為空心薄壁墩（下頁圖3），高161 m，其墩高位居國(guó)內(nèi)同類型橋梁中第6位，采用爬模施工。

由于本橋結(jié)構(gòu)體系復(fù)雜，同時(shí)橋址區(qū)位于峽谷風(fēng)口地帶、地震基本烈度為Ⅷ度的高海拔區(qū)域（橋面海拔約2 460 m），加之高溫差、高紫外線、干旱等氣候條件的影響，使得施工過程中不確定因素較多，施工難度較大。針對(duì)該橋建設(shè)條件的特殊性，應(yīng)加強(qiáng)對(duì)施工技術(shù)和方案的研究［3］，開展施工過程風(fēng)險(xiǎn)評(píng)估工作。

4.2 實(shí)橋應(yīng)用

由于超高墩連續(xù)剛構(gòu)橋主墩施工控制參數(shù)較主梁少，沒有預(yù)應(yīng)力束張拉控制等參數(shù)，且墩身截面較主梁尺寸較小，不利于不平衡荷載等工況的模擬，部分主墩施工風(fēng)險(xiǎn)指標(biāo)難以量化。因此，采用基于博弈論和BP神經(jīng)網(wǎng)絡(luò)的風(fēng)險(xiǎn)預(yù)測(cè)模型對(duì)該橋高墩施工風(fēng)險(xiǎn)進(jìn)行預(yù)測(cè)。

通過典型案例分析并結(jié)合工程實(shí)際，識(shí)別高墩施工風(fēng)險(xiǎn)因素進(jìn)而建立具有層次結(jié)構(gòu)的風(fēng)險(xiǎn)預(yù)測(cè)指標(biāo)體系，具體如圖4、表1所示。

基于上述風(fēng)險(xiǎn)預(yù)測(cè)指標(biāo)體系，分別運(yùn)用AHP、熵權(quán)法對(duì)各層評(píng)價(jià)指標(biāo)進(jìn)行求解。由于篇幅限制，此處直接給出各評(píng)價(jià)指標(biāo)的權(quán)重ω1、ω2，如式（15）、式（16）所示。

ω1=0.107，0.088，0.066，0.396，0.134，0.111，0.052，0.046（15）

ω2=0.110，0.053，0.055，0.397，0.170，0.111，0.057，0.047（16）

由博弈權(quán)重集化式（10）～（14），求出該項(xiàng)目施工風(fēng)險(xiǎn)評(píng)價(jià)指標(biāo)的綜合權(quán)向量ω，如式（17）所示。

ω=0.108，0.077，0.063，0.396，0.145，0.111，0.053，0.046（17）

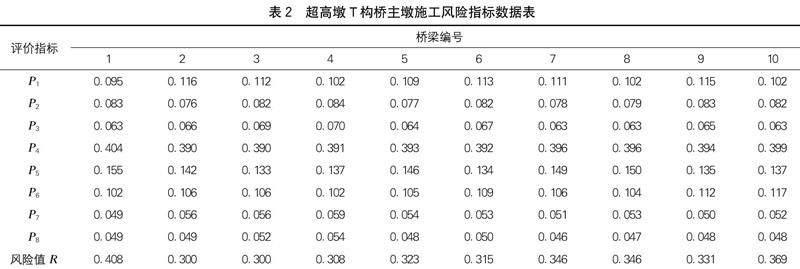
利用Matlab軟件創(chuàng)建該指標(biāo)體系下的BP神經(jīng)網(wǎng)絡(luò)。為確保網(wǎng)絡(luò)（函數(shù)）的準(zhǔn)確性，選取10座經(jīng)項(xiàng)目驗(yàn)證的超高墩T構(gòu)橋（如赫章特大橋等）作為網(wǎng)絡(luò)的訓(xùn)練和測(cè)試樣本。隨機(jī)抽取9組數(shù)據(jù)作為訓(xùn)練集，1組數(shù)據(jù)作為測(cè)試集，具體數(shù)據(jù)如下頁表2所示。

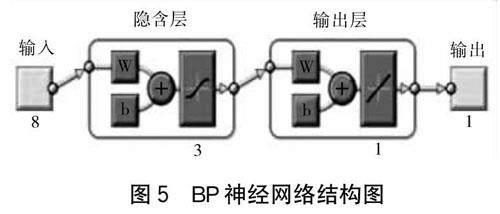
將評(píng)價(jià)指標(biāo)Pi作為輸入層神經(jīng)元，將風(fēng)險(xiǎn)值R作為輸入層神經(jīng)元，采用試湊法確定網(wǎng)絡(luò)收斂最快、誤差最小時(shí)對(duì)應(yīng)的隱藏層節(jié)點(diǎn)數(shù)為3［7］，其結(jié)構(gòu)如下頁圖5所示。

然后將所有樣本代入后檢驗(yàn)得，10組數(shù)據(jù)平均相對(duì)誤差為0.489%，最大誤差為1.57%，故該網(wǎng)絡(luò)擬合較好，可用于超高墩T構(gòu)橋主墩施工風(fēng)險(xiǎn)預(yù)測(cè)。

將龐納子大橋高墩施工風(fēng)險(xiǎn)評(píng)價(jià)指標(biāo)的綜合權(quán)向量ω輸入上述網(wǎng)絡(luò)，得到風(fēng)險(xiǎn)預(yù)測(cè)值為0.348，由表3可判定該項(xiàng)目風(fēng)險(xiǎn)較低，在可接受范圍內(nèi)。

根據(jù)綜合權(quán)向量ω及表2中風(fēng)險(xiǎn)指標(biāo)Pi-風(fēng)險(xiǎn)值R之間的映射關(guān)系可知，該項(xiàng)目施工主要風(fēng)險(xiǎn)因素依次為：墩身垂直度、風(fēng)荷載、日照溫差、混凝土強(qiáng)度等。其中，風(fēng)荷載、日照溫差均會(huì)影響高墩的垂直度，因此建議在該項(xiàng)目施工過程中對(duì)其墩身垂直度進(jìn)行風(fēng)險(xiǎn)監(jiān)控。

5 結(jié)語

（1）基于博弈論和BP神經(jīng)網(wǎng)絡(luò)的橋梁風(fēng)險(xiǎn)預(yù)測(cè)模型以減少主觀成分為原則，通過提高評(píng)價(jià)指標(biāo)的準(zhǔn)確度、全面性和科學(xué)性進(jìn)而獲得可靠的風(fēng)險(xiǎn)預(yù)測(cè)值。

（2）由預(yù)測(cè)模型求得龐納子大橋高墩施工風(fēng)險(xiǎn)值為0.348，判定該項(xiàng)目風(fēng)險(xiǎn)較低，在可接受范圍內(nèi)。

（3）該項(xiàng)目施工主要風(fēng)險(xiǎn)因素依次為：墩身垂直度、風(fēng)荷載、日照溫差、混凝土強(qiáng)度等。

（4）建議在該項(xiàng)目施工過程中對(duì)其墩身垂直度進(jìn)行風(fēng)險(xiǎn)監(jiān)控。

參考文獻(xiàn)

［1］袁光杰.復(fù)雜環(huán)境下超高墩T構(gòu)橋施工過程風(fēng)險(xiǎn)分析與應(yīng)對(duì)措施研究［D］.重慶：重慶交通大學(xué)，2020.

［2］姜越川.連續(xù)剛構(gòu)橋施工風(fēng)險(xiǎn)評(píng)估研究［J］.中外建筑，2011（2）：77-78.

［3］李凌俊.超高墩連續(xù)剛構(gòu)橋施工期內(nèi)風(fēng)險(xiǎn)評(píng)估研究［D］.重慶：重慶交通大學(xué)，2012.

［4］金 晶，李宗昊，朱 亮，等.BP神經(jīng)網(wǎng)絡(luò)在鐵路建設(shè)風(fēng)險(xiǎn)評(píng)估中的應(yīng)用［J］.鐵道工程學(xué)報(bào)，2019，36（3）：103-109.

［5］吳小萍，儲(chǔ)誠(chéng)誠(chéng)，李月光，等.博弈論在高速公路施工期環(huán)境影響評(píng)價(jià)中的應(yīng)用［J］.鄭州大學(xué)學(xué)報(bào)（工學(xué)版），2012，33（6）：36-40.

［6］蘇觀南，付修慶，劉天祥.改進(jìn)的博弈論綜合權(quán)重在大壩安全綜合評(píng)價(jià)中的應(yīng)用［J］.中國(guó)農(nóng)村水利水電，2014（11）：82-85.

［7］王飛球，黃健陵，符 競(jìng)，等.基于BP神經(jīng)網(wǎng)絡(luò)的跨既有線高速鐵路橋梁施工安全風(fēng)險(xiǎn)評(píng)估［J］.鐵道科學(xué)與工程學(xué)報(bào)，2019，16（5）：1 129-1 136.

［8］方 鴻.跨鐵路高墩連續(xù)剛構(gòu)橋穩(wěn)定性研究及風(fēng)險(xiǎn)分析［D］.長(zhǎng)沙：長(zhǎng)沙理工大學(xué)，2012.

［9］納啟財(cái).高原地區(qū)環(huán)境及養(yǎng)護(hù)條件對(duì)混凝土性能的影響［J］.混凝土與水泥制品，2016（1）：10-13.

［10］張謝東，郭俊峰，余建宜，等.山區(qū)高墩大跨橋梁施工過程中的風(fēng)險(xiǎn)識(shí)別［J］.橋梁建設(shè)，2008（6）：80-83.

［11］虞 輝，李利軍，張 溪.山區(qū)高墩連續(xù)剛構(gòu)橋安全風(fēng)險(xiǎn)評(píng)估研究［J］.現(xiàn)代交通技術(shù)，2012，9（1）：29-32.

作者簡(jiǎn)介：黃 偉（1988—），研究方向：橋梁風(fēng)險(xiǎn)評(píng)估、橋梁健康監(jiān)測(cè)。