一種有效的周期高效用序列模式增量挖掘算法

摘 要：周期高效用序列模式挖掘（PHUSPM）因其能夠發現時間序列中更具實際價值的規律性模式而備受關注，但現有的PHUSPM算法難以有效地處理數據集的增量更新，且未考慮大規模數據下算法的向下閉包性和復雜性。針對該問題，提出了IncPUS-Miner算法，有效地實現了周期高效用序列模式（PHUSPs）的增量挖掘。IncPUS-Miner引入了一種名為pu-tree的新型數據結構，每個樹節點對應一個更新效用列表（UUL）用于存儲相應序列的輔助信息，當有增量數據加入時，該結構使得項目信息能夠靈活更新，從而增強了算法的動態適應性和可擴展性。此外，還提出了兩種新的序列效用上界PUB和EUB，以及兩種相應的剪枝策略，有效地減少了計算負擔。實驗結果表明，在真實數據集上，IncPUS-Miner算法可以有效地增量挖掘PHUSPs，與其他算法相比，在運行效率和內存消耗上展現出了優越的性能。

關鍵詞：增量挖掘； 高效用序列模式； 周期序列模式； 序列模式挖掘

中圖分類號：TP301.6 文獻標志碼：A

文章編號：1001-3695（2024）08-008-2301-08

doi：10.19734/j.issn.1001-3695.2023.12.0607

Effective incremental mining algorithm forperiodic high-utility sequential patterns

Xun Yaling， Ren Ziqian， Yan Haibo

（College of Computer Science & Technology， Taiyuan University of Science & Technology， Taiyuan 030024， China）

Abstract：Periodic high utility sequential pattern mining（PHUSPM） has attracted much attention because it can find more practical regular patterns in time series. 0WckXHg/1zH9NyqfpE2D7w==However， existing PHUSPM algorithms struggle to effectively handle incremental updates and overlook the downward closure property and complexity of the algorithm in large-scale data. To solve this problem， this paper proposed an IncPUS-Miner algorithm， which effectively realized the incremental mining of periodic high-utility sequential patterns（PHUSPs）. IncPUS-Miner introduced a novel data structure called pu-tree. Each tree node corresponded to an updated utility list（UUL） to store the auxiliary information of the corresponding sequence. When incremental data was added， this structure allowed flexible updates to project information， thereby enhancing the dynamic adaptability and scalability of the algorithm. In addition， this paper proposed two new upper boundsdn8fJNqDdQNk1RMoa5x/Zw== of sequence utility， PUB and EUB， and two corresponding pruning stra-tegies， which effectively reduced the computational burden. The experimental results show that the IncPUS-Miner algorithm effectively realizes the incremental mining of PHUSPs on real data， and shows superior performance compared with other algorithms.

Key words：incremental mining; high utility sequential pattern; periodic sequential pattern; sequential pattern mining

0 引言

高效用序列模式挖掘（HUSPM）是數據挖掘的焦點之一，其任務是在定量序列中找到所有具有高效用的子序列［1］。HUSPM的效用度量與傳統序列模式挖掘［2］的支持度量不同，不具有單調性或反單調性，無法直接用于搜索空間剪枝［3］。因此，如何制定更有效的效用上限，以優化搜索空間并提高性能是HUSPM面臨的挑戰之一［4，5］。

隨著大數據時代的興起，新數據不斷產生。由于靜態方法需要重新掃描整個數據集執行挖掘，導致增量挖掘過程非常耗時。因此，一些能夠有效處理增量數據的序列數據挖掘算法應運而生［6～12］。Yun等人［7］提出了基于索引列表的增量高效用模式挖掘（IIHUM）算法，僅需一次數據集掃描。Kim等人［8］提出了基于樹狀結構的高平均效用項集（IMHAUI）的增量挖掘算法。Wang等人［9］采用基于候選模式樹結構的算法來實現增量挖掘高效用序列模式。這些增量算法旨在處理高效用模式的問題，未考慮模式的周期性約束。毛伊敏等人［10］提出了改進的并行關聯規則增量挖掘算法，為處理大規模數據集的挖掘提供了有效方法。

周期性高效用序列模式挖掘（PHUSPM）發現的模式不僅具有高效用特性，還呈現周期性出現規律［13］，在實際應用中具有重要意義［14］。例如，在市場分析中，分析消費者購買習慣的周期性和高效用模式可幫助商家優化促銷策略。在基因序列分析中［15］，尋找具有特定周期性和高效用的模式有助于理解生物過程中的重要事件。近年來，Fournier-Viger及其團隊［16］提出了PHM算法，用于尋找周期性高效用項集。Dinh等人［13］提出PHUSPM算法，但由于未采用剪枝策略，導致執行時間長且內存占用大。Dinh等人［17］提出了基于PUSP結構的PUSOM算法，可以發現序列數據庫中的所有PHUSPs，但不適用于動態數據集。盡管已有一些有效的周期性高效用序列模式挖掘算法，PHUSPs挖掘仍面臨以下問題和挑戰：

a）數據集的增量更新。傳統的PHUSPM算法在處理新數據時需要重新從頭開始挖掘，導致大量重復開銷，難以有效應對數據集變化。

b）向下閉包性。周期高效用模式挖掘考慮向下閉包性質，增加了算法復雜性，特別是在處理動態序列數據時需要不斷更新向下閉包性。

c）復雜性和效率。現代大規模數據集的增加使得周期高效用模式挖掘算法需要在保持高效性的同時處理復雜性。設計更高效的數據結構和算法是必要的，以在大規模數據上進行快速挖掘。

針對上述問題，本文提出一種新的增量挖掘算法IncPUS-Miner，允許在現有模式的基礎上高效地更新和增加新模式，而無須重新掃描整個數據集，從而減少了不必要的開銷。其主要貢獻總結如下：

a）提出一種新的數據結構，稱為pu-tree，并設計了樹節點更新效用列表（UUL），用于存儲相應序列的輔助信息，以便在數據更新時快速獲取序列的效用等輔助信息，避免不必要的重復計算開銷。基于該數據結構提出一個新的增量周期性高效用模式挖掘算法IncPUS-Miner，以有效挖掘大規模和不斷更新的序列數據中的周期性高效用模式。

b）為了減少冗余計算，定義了兩個新的序列效用上界，分別稱為PUB和EUB，并提出了兩種相應的剪枝策略，以顯著提高挖掘效率。

c）在真實數據集上進行大量的實驗表明，IncPUS-Miner算法能夠有效地增量挖掘PHUSPs，算法性能優于其他對比算法。

1 相關定義

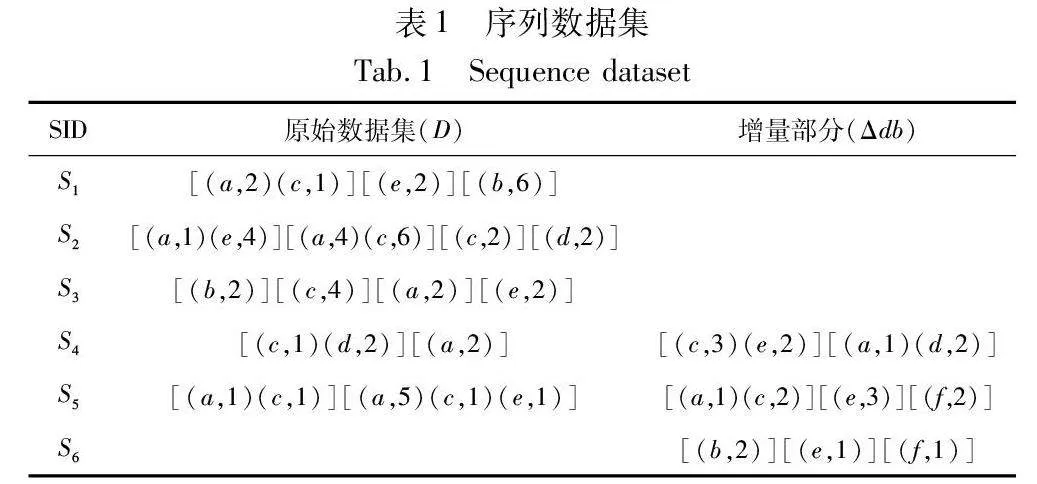
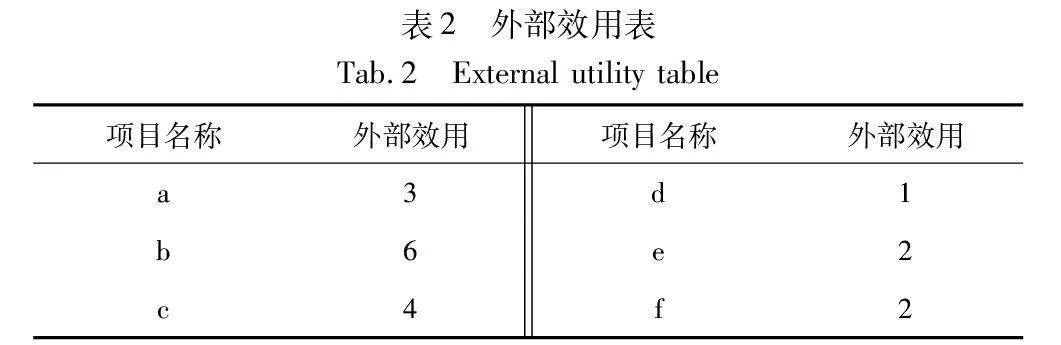
I={i1，i2，…，in}，n≥1是一組包含n個項目的有限集。序列數據庫中每個項記為（ik，qk），其中ik∈I（1≤k≤n），qk表示內部效用值，外部效用值用p（ik）表示。在表1所示的序列數據集中，（a，2）表示項目a的內部效用值為2。表2體現了每個項目對應的外部效用，如a的外部效用值為3。

T=［（i1，q1），（i2，q2），…，（im，qm）］可以表示為一條事務。一般情況下，事務中的項目順序按照字典順序來排序。表1給出的序列數據庫包含6條序列，每個序列Si（1≤i≤6）又包含多條事務T。比如S1中包含了3條事務，分別是T1=［（a，2）（c，1）］，T2=［（e，2）］，T3=［（b，6）］。

模式t屬于項集，它的表示方法有t1=〈（i1i2i3）〉和t2=〈i1i2i3〉，模式t1表示包含的三個項存在于同一事務中，而模式t2表示三個項各自存在于不同事務里。

定義1 項目效用。對于項目i，其在序列S的第j個事務中的效用定義為

U（i，j，S）=q（i，j，S）×p（i）（1）

例1 U（a， 1， S2）= 3，U（a ， 2， S2）= 12。

定義2 項集效用。項集X在序列S的第j個事務中的效用被定義為

U（X，j，S）=∑i∈XU（i，j，S）（2）

例2 U（〈ac〉，〈1，2〉，S2）=U（a，1，S2）+U（c，2，S2）=27。

定義3 模式在序列中的效用。模式t在序列S中的效用記為U（t，S），定義為模式t在序列S中的所有實例效用的最大值。其中，〈j1，j2，…，j|s|〉是模式t在序列S中出現的事務號的集合。

U（t，S）=max{∑i∈tU（i，〈j1，j2，…，j|S|〉，S）}（3）

例3 給定一個模式t=〈ac〉，它在序列S2出現的事務號集合為〈〈1，2〉，〈1，3〉，〈2，3〉〉，故U（〈ac〉，S2）=max{U（〈ac〉，〈1，2〉，S2），U（〈ac〉，〈1，3〉，S2），U（〈ac〉，〈2，3〉，S2）}=max{27，11，20}=27。

定義4 模式在數據集中的效用。模式t在數據集D中的效用記為

UD（t）=∑S∈D∧tSU（t，S）（4）

定義5 高效用序列模式。當模式t的效用UD（t）≥minutil時，模式t為序列數據庫D中的高效用序列模式，否則認為模式t是低效用模式。其中，minutil是用戶給定的最小效用閾值。

例4 給定模式t=〈ac〉，minutil為20，根據表1所示，模式t=〈ac〉只出現在S2和S5兩個序列中，所以UD（〈ac〉）=U（〈ac〉，S2）+U（〈ac〉，S5）=27+7=34。34>20，因此，模式t=〈ac〉是高效用模式。

給定數據集D={S1，S2，…，Sn}和模式t，模式t在數據集D中出現的序列列表為S（t，D）={Si1，Si2，…，Sik}，其中1≤i1<i2<…< ik≤n，Sik是指第ik條序列。模式t在D中的擴展序列列表為g（t，D）={Si0，Si1，Si2，…，Sik}，Sid（Si0）=0。

定義6 模式的周期。在g（t，D）中連續出現的兩個序列之間相距的序列數稱為這兩個序列的周期，記為per，即式（5）。Si（k+1）是指數據集D中的最后一條序列，Sid（Si（k+1））=|D|=n。

per（t，ik）=Sid（Si（k+1））-Sid（Sik）（5）

例5 根據表1的數據集D（n=5），模式t=〈ac〉的擴展序列列表g（〈ac〉，D）={S0，S2，S5}，即i0=0，i1=2，i2=5。根據式（5），得到per（〈ac〉，i0）=2-0=2，per（〈ac〉，i1）=5-2=3，per（〈ac〉，i2）=n-5=0，因此per（〈ac〉）={2，3，0}。對于模式t=〈（ac）〉，它表示項目a和c存在于同一事務中，它的序列列表S（〈（ac）〉，D）={S1，S2，S5}， g（〈（ac）〉，D）={S0，S1，S2，S5}，計算得到per（〈（ac）〉）={1，1，3，0}。

下面介紹三個周期性度量，分別是最大周期度量、最小周期度量和平均周期度量。這三種度量為用戶發現PHUSPs提供了更多的靈活性，比如，用戶可以選擇通過使用三種度量或只使用最大周期度量來找到序列數據庫中的周期模式。

定義7 周期性度量。模式t最大周期值記為maxper（t）=max（per（t）），最小周期值是minper（t）=min（per（t）），平均周期值是avgper（t）=∑per（t）|per（t）|。

例6 根據定義6中的示例可知，模式t=〈ac〉的周期per（〈ac〉）={2，3，0}，那么模式t的最大周期值為maxper（t）=max{2，3，0}=3，最小周期值是minper（t）=min{2，3，0}=0，平均周期值是avgper（t）=5/3=1.67。

絕大多數的周期模式挖掘算法僅僅依賴于最大周期度量（maxPer），這可能導致一些模式由于滿足最大周期約束而被挖掘出來，盡管它們只在少數序列中出現。這種單一度量的方法存在不足之處。因此，本文算法選擇綜合三種度量，以提供更多靈活性給用戶的同時，確保挖掘出更有實際意義的模式。

定義8 周期高效用序列模式。給定模式t以及5個用戶給定的閾值（minutil，maxPer，minPer，maxAvg，minAvg）。如果模式t同時滿足以下兩個條件，則被稱為周期高效用模式（PHUSP）：a）模式t滿足定義5，即UD（t）≥minutil；b）模式t滿足maxper（t）≤maxPer，minper（t）≥minPer且minAvg≤avgper（t）≤maxAvg。

定義9 插入序列。當序列S插入數據集D后，獨立構成一條新的序列時，將S稱為插入序列。在表1中，S6是插入序列。

定義10 附加序列。當序列S插入數據集D后，附加在原始數據集中的序列S0結尾，從而形成S0·S形式的新序列，這樣的序列稱為附加序列。在表1中，S4和S5是附加序列。

定義11 模式連接。模式的擴展分為I-連接和S-連接［5］。對于給定模式t，I-連接指的是將與模式t在同一事務中存在的項i附加到t后，形成一個新的項集，表示為〈t⊕i〉。類似地，S-連接表示將模式t后續事務中的項i附加到t后，形成一個新的項集，表示為〈ti〉。這兩種連接方式是模式擴展的關鍵策略。

2 IncPUS-Miner算法

IncPUS-Miner算法采用pu-tree結構，通過效用列表存儲序列的相關信息，以便在更新數據時快速獲取相關信息。同時設計了兩個序列效用上界及兩種剪枝策略，縮減了算法的搜索空間，以進一步提高算法性能。

2.1 序列效用上界

在文獻［5］中提出了兩個效用上界，即前綴擴展效用（PEU）和簡化序列效用（RSU）。PEU上界策略需要計算模式t在序列中每次出現時的效用值及當下位置的剩余效用之和，再選擇最大值作為模式在該序列的PEU值，這樣的計算過程復雜。為了提高挖掘效率，在本節中提出了兩個新的序列效用上界，稱為前綴-效用上界（PUB）和擴展-效用上界（EUB），在2.1.1節和2.1.2節中分別給出了定義。

2.1.1 前綴-效用上界（PUB）

假如模式t在序列S中出現的位置為j：〈j1，j2，…，jm〉，模式t在序列S中的PUB值定義如式（6），j1是指模式t首次出現的位置。模式t的PUB值表示如式（7）所示。

PUB（t，S）=Umax（t，S）+RU（t，j1，S） RU＞00其他（6）

PUB（t）=∑t∈S∩S∈DPUB（t，S）（7）

模式t在序列S中的PUB值指的是模式t在序列中出現的最大效用值與模式t首次出現位置的剩余效用值之和。

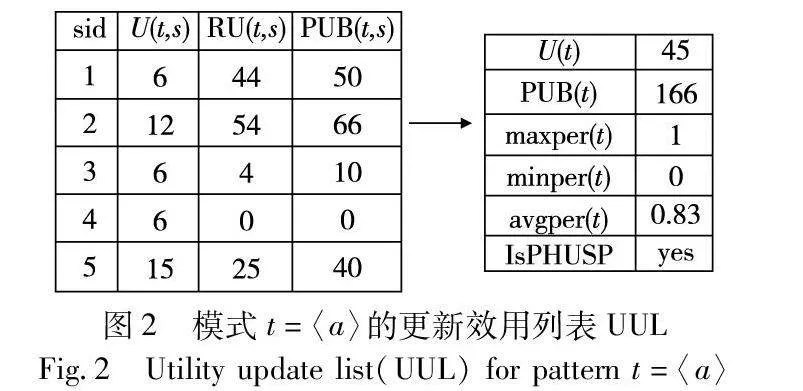
例7 在表1的原始數據集D中，模式t=〈a〉在序列S1中的PUB值表示為PUB（t，S1）=U（〈a〉，S1）+RU（〈a〉，1，S1）=6+44=50，同理計算得到PUB（t，S2）=12+54=66，PUB（t，S3）=6+4=10，PUB（t，S4）=0，PUB（t，S5）=15+25=40。因此，模式t在數據集D中的PUB值表示為PUB（〈a〉）=166。

定理1 向下閉包性質。給定兩個模式t和t′，如果t′包含t（t′是t的擴展模式），那么滿足PUB（t′）≤PUB（t）。

證明 假設序列S中存在兩個模式t和t′，模式t′是t的擴展模式，表示為t′=t·t″。模式t在序列S中首次出現位置的剩余效用為RU（t，j1，S），且RU（t，j1，S）≥Umax（t″）+RU（t″，j1，S），根據式（6），可得PUB（t，S）≥Umax（t，S）+Umax（t″）+RU（t″，j1，S），又因為RU（t″，j1，S）=RU（t′，j1，S），所以PUB（t，S）≥PUB（t′，S）。

例8 給定兩個模式t=〈a〉和t′=〈ac〉，t′是t的擴展模式。在表1的原始數據集D中，模式t=〈a〉出現在序列S1、S2、S3、S4、S5中，模式t′=〈ac〉只出現在序列S2、S5中，計算得到PUB（〈a〉）=166，PUB（〈ac〉）=46。由此可以得出，如果模式t′是模式t的超集，則滿足PUB（t′）≤PUB（t）。

定理2 給定一個模式t，對于它的每個擴展模式t′，都滿足U（t′）≤PUB（t）。

證明 假設模式t出現在序列S中，p是S中t的實例擴展位置（即模式t最后項出現的位置）。由于t是t′的前綴，若假設t′=t·t″，其中t″不為空集。那么模式t′在S中的效用包括兩部分：一是模式t的擴展位置p處的效用；二是t″的效用（t″一定出現在擴展位置p之后）。因此，模式t′的效用可以表示為U（t′）=U（t）+U（t″），U（t″）屬于剩余序列的一個子序列。而PUB（t）=Umax（t）+RU（t，j1），即模式t在序列S中出現的最大效用值與模式t首次出現位置的剩余效用值（即最大剩余效用值）之和。由于U（t）<Umax（t），U（t″）<RU（t，j1），可以得到U（t′）≤PUB（t）。

2.1.2 擴展-效用上界（EUB）

假如在序列S中，模式t′由模式t經過I-連接或S-連接擴展而來，模式t′在序列S中的EUB值記為EUB（t′，S），表示如式（8）所示。模式t′在數據集D中的EUB值記為EUB（t′），表示如式（9）所示。

EUB（t′，S）=PUB（t，S） tS∧t′S0其他（8）

EUB（t′）=∑S∈DEUB（t′，S）（9）

定理3 給定一個模式t，對于它的每個擴展模式t′，都滿足U（t′）≤ EUB（t′）。

證明 假設模式t可以通過I-連接或S-連接擴展生成模式t′。根據定理2的證明可知，U（t′）≤PUB（t），在式（8）中表示EUB（t′，S）=PUB（t，S），因此，可以推出U（t′）≤EUB（t′）的結論。

2.2 剪枝策略

根據PUB和EUB這兩個效用上界，對應提出了兩種剪枝策略，即前綴效用上界策略和擴展效用上界策略。

策略1 前綴效用上界策略。假設t和minutil分別是候選模式和最小效用閾值。如果PUB（t）≤minutil，那么算法不需要檢查模式t及其擴展后代。

該剪枝策略可以防止算法考慮沒有希望的項，因為PUB上界具有向下閉包屬性，當PUB（t）≤minutil時，就認為模式t及它的所有擴展模式都是無用的。

策略2 擴展效用上界策略。設t和minutil分別是候選模式和當前最小效用閾值，模式t通過I-連接或S-連接擴展生成模式t′。當EUB（t）≤minutil時，算法將停止擴展模式t′。

根據定理3，EUB（t）是模式t以及它所有后代的效用上界，因此，當EUB（t）<minutil時，以t為根的子樹可以安全地修剪，并不會影響挖掘結果。

由于需要考慮模式的周期性約束，下面介紹第三種剪枝策略［16］。

定理4 最大周期值單調性。給定兩個模式t和t′，其中t′是t的擴展模式。因此，maxper（t′）≥maxper（t）。

證明 若S（t′）和S（t）是分別包含模式t′和t的序列集合。由于tt′，所以S（t′）S（t）。當S（t′）=S（t）時，模式t和t′有相同的周期，即maxper（t）=maxper（t′）。若S（t′）S（t）時，per（t′）中的任何周期都不能小于per（t）中的周期，所以maxper （t′）>maxper（t）。

策略3 最大周期閾值修剪策略。假設t是一個出現在數據庫D中的高效用模式，maxPer是用戶給定的最大周期閾值。如果maxper（t）>maxPer，則模式t及其后代都不是周期高效用模式。

根據定義8，如果模式t不滿足maxper（t）>maxPer，那么模式t就不是周期高效用模式。通過定理4可知，模式t的所有后代的maxper值都大于maxPer，故它們都不是PHUSPs。

2.3 pu-tree結構

文獻［10］提出了一種有效的基于候選模式樹結構的增量算法，該算法能夠在不斷更新的數據庫中挖掘高效用序列模式，但未考慮模式的周期性。為了更全面地處理模式的效用和周期相關數據，提出了一種新的數據結構，稱為pu-tree。該結構以樹狀形式組織，其中每個樹節點代表一個項目，每個樹路徑代表一個模式或模式的一部分。算法掃描一次數據庫后，構建這個樹，并將模式的相關信息都存儲在該樹節點的更新效用列表（UUL）中，以便在不需要重新計算的情況下快速獲取模式的相關信息。UUL包含的內容有：

a）U（t）：模式t在輸入數據集中的效用值，即模式t在所有序列中的最大效用值之和。

b）PUB（t）：模式t在輸入數據集中的PUB值，即模式t在所有序列中的PUB值之和。

c）maxper（t）、minper（t）、avgper（t）：模式t在輸入數據集中的最大周期值、最小周期值和平均周期值。

d）IsPHUSP：若模式t是周期高效用模式，就記為yes，否則記為no。

2.4 算法描述

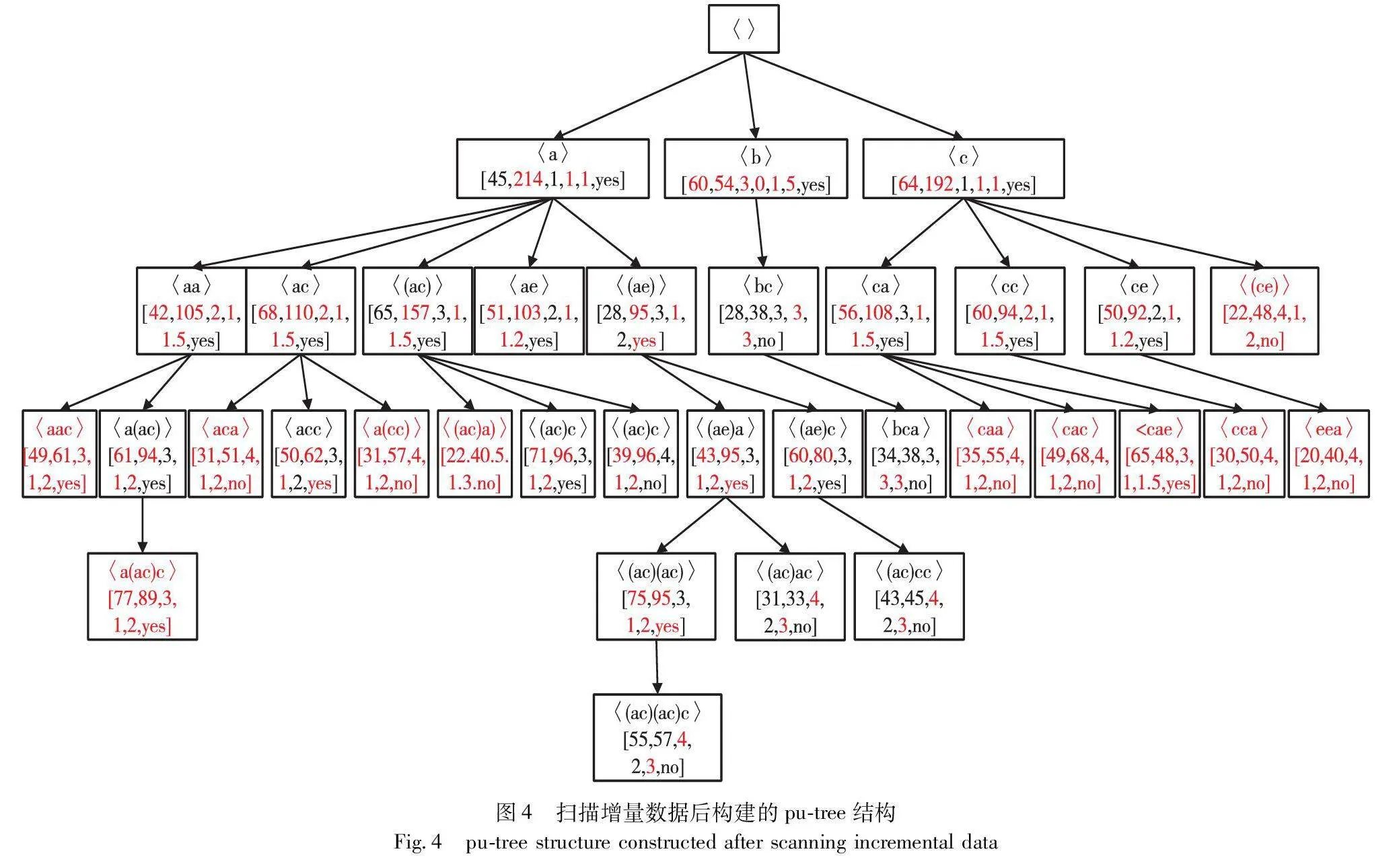
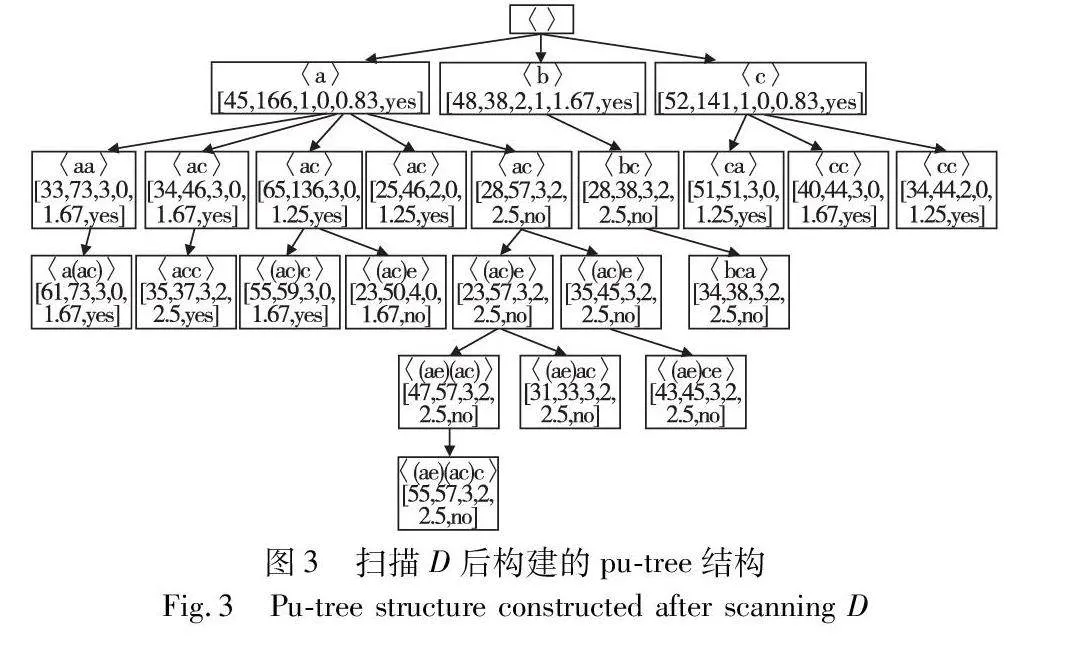
IncPUS-Miner包括初始和增量兩個階段。在初始階段，提出了算法PUS-Miner，實現從原始數據庫D中挖掘PHUSPs。當加入增量數據后， IncPUS-Miner算法能夠有效處理增量數據，更新pu-tree結構，挖掘出新的PHUSPs。現設定閾值：minutil=30，maxPer=3，minPer=0，minAvg=0.5，maxAvg=2。根據表1的示例數據集，在圖1展現了所提出的增量挖掘方法的整體體系結構。圖2展示了掃描原始數據集D后，模式t=〈a〉的UUL列表結構示例。圖3顯示了掃描原始數據集D后構建的pu-tree結構，圖4是加入增量數據后的pu-tree結構。

2.4.1 初始挖掘階段

如算法1所示，PUS-Miner算法的主要思路是構建候選模式樹pu-tree，再以深度優先搜索（DFS）的方式從原始數據集中提取具有高效用值的模式（PHUSP）。在處理每個節點t時，PUS-Miner首先檢查PUB（t）是否小于minutil。若PUB（t）小于minutil，那么PUS-Miner可以跳過節點t的擴展步驟。當PUB（t）大于或等于minutil時，PUS-Miner會掃描D中t的投影數據庫，以查找所有具有高EUB值的擴展序列t′。對于每個t′，PUS-Miner會構建相應的節點結構，將其作為t的子節點。如果t′是一個周期性高效用模式，PUS-Miner將其添加到PHUSP集中，并以t′為輸入遞歸調用PUS-Miner算法，以繼續擴展t′。由于應用了效用上界剪枝策略，算法PUS-Miner可以考慮較少的項目集，優化了算法的時間復雜度。

算法1 PUS-Miner（t）

輸入：序列數據集D；模式t的投影數據集D|t；最小效用閾值ε；最大周期閾值maxPer；最小周期閾值minPer；最大平均周期閾值maxAvg；最小平均周期閾值minAvg。

輸出：PHUSPs的集合（PHUSP）。

1 scan D to calculate the utility values of all 1-pattern;

//掃描數據集D，計算所有1-模式的效用值

2 remove the utility values of 1-pattern less than ε;

//移除效用值小于ε的1-模式

3 initialize an set PHUSP; //初始化PHUSP集

4 scan D|t once to find extend-pattern，

add I-Extension items of t to i-list;

add S-Extension items of t to s-list;

//掃描模式t的投影數據集D，發現模式t的所有擴展項

5 remove low EUB items from i-list and s-list； /*從擴展模式列表i-list和s-list中刪除低EUB值的項*/

6 for each item i∈i-list and s-list do

//對于i-list和s-list中的每個項

7 if i∈i-list then //如果項i存在于i-list中

8 t′←〈t⊕i〉 //經I-連接，模式t和項i組成新模式t′

9 if i∈s-list then //如果項i存在于s-list中

10 t′←〈ti〉 //經S-連接，模式t和項i組成新模式t′

11 BuildNode（t′） and add t′ to pu-tree;

//構造模式t′的樹節點，并添加它到結構pu-tree中

12 if（maxper（t′）≤maxPer） then //剪枝策略3

13 if（PUB（t′）≥ε） //剪枝策略1

14 IsPeriodic（S（t′），minPer，maxPer，maxAvg，minAvg）

//調用IsPeriodic方法，判斷t′是否滿足其余周期度量

15 if true then //若滿足

16 insert t′ into PHUSP; //將模式t′存入PHUSP集

17 PUS-Miner（t′）; //遞歸調用PUS-Miner（t′），繼續擴展t′

18 return;

2.4.2 增量挖掘階段

載入增量數據后，原始數據集D更新為D′。數據集D′可以看作兩部分：一部分是數據集更新時并沒有發生改變的序列，將這部分稱為無更新數據，記為NDB；另一部分是在數據集更新時有發生變化的序列，稱為更新數據，記為UDB。例如，在表1中，NDB包含序列S1、S2、S3，UDB包含序列S4、S5、S6、S7。另外，對于數據集更新后的每個模式t，都必須考慮以下兩種情況：

a）模式t在D和D′中都屬于周期高效用模式；

b）模式t在D中不屬于周期高效用模式，但在D′中屬于周期高效用模式。

算法2 IncPUS-Miner（t）

輸入：更新數據集D′；模式t的投影數據集D′|t；最小效用閾值ε；最大周期閾值maxPer；最小周期閾值minPer；最大平均周期閾值maxAvg；最小平均周期閾值minAvg；PHUSP集。

輸出：新的PHUSPs集（PHUSP）。

1 if all sequences in UDB|t are empty sequences then

2 return;//當更新數據UDB為空時，返回

3 if PUBD′（t）<ε then

4 return; //當模式t的PUB值小于ε時，返回

5 scan D′|t to calculate the EUB of all t’s extension sequences;

//掃描模式t的投影數據集D′，計算EUB（t′）

6 for each t’s extension sequences t′∈D′ do

7 if EUBD′（t′）≥ε then //剪枝策略2

8 if t′∈UDB then //若模式t′屬于更新數據

9 if t′∈pu-tree then//模式t′已存在于pu-tree結構

10 UpdateNode（t′）;

//更新模式t′在pu-tree結構中的相關信息

11 IncPUS-Miner （t′）;//遞歸調用IncPUS-Miner方法

12 else //若模式t′不存在于pu-tree結構

13 BuildNode（t′） and add t′ to pu-tree;

//構造模式t′的樹節點，并添加它到結構pu-tree中

14 if （maxper（t′）≤maxPer） then //剪枝策略3

15 if（PUB（t′）≥ε） then //剪枝策略1

16 IsPeriodic（S（t′）， minPer， maxPer， maxAvg， minAvg）

//調用IsPeriodic方法，判斷t′是否滿足其余周期度量

17 if true then //若滿足

18 insert t′ into PHUSP; //將t′存入PHUSP集

19 PUS-Miner（t′）; /*遞歸調用PUS-Miner（t′），繼續擴展模式t′*/

20 else

21 skip node t′;//跳過模式t′

2.4.3 IsPeriodic方法

在算法3中體現了IsPeriodic方法的具體操作，該方法用來判斷高效用模式是否具有周期性。IsPeriodic方法首先掃描模式t出現的序列集S（t），計算其最小周期值、最大周期值和平均周期值（第1～3行）。如果t是一個周期模式（第4行），則該過程返回true（第5行）；否則，返回false（第7行）。

算法3 IsPeriodic方法

輸入：模式t出現的序列集S（t）； 最大周期閾值maxPer；最小周期閾值minPer；最大平均周期閾值maxAvg；最小平均周期閾值 minAvg。

輸出：如果模式t是周期模式，返回true；否則，返回flase。

1 calculate maxper（t）=max（per（t））;//計算t的最大周期值

2 calculate minper（t）=min（per（t））;//計算t的最小周期值

3 calculate avgper（t） = |S|/（S（t）+1）;//計算t的平均周期值

4 if （maxper（t）≤maxPer & minper（t）≥minPer & minAvg≤avgper（t）≤maxAvg） then //判斷模式t是否滿足周期性條件

5 return true; //若滿足，返回true

6 else

7 return false; //若不滿足，返回false

3 實驗評價

為了評估IncPUS-Miner算法的有效性，選擇了三種先進的算法作為對比算法，分別為PHM算法［16］、PUSOM算法［17］和FHUQI- Miner算法［18］。

3.1 實驗環境

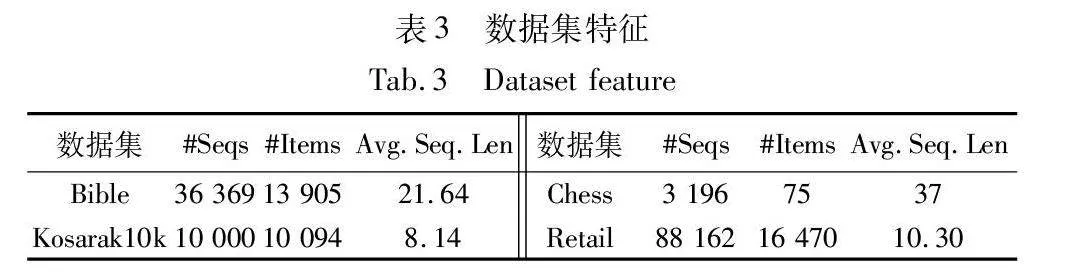
實驗運行環境為一臺1.90 GHz CPU和16 GB內存，運行64位微軟Windows 11的計算機，基于Java編寫。實驗使用了4個真實數據集來評估算法的性能，其特征總結如表3所示。所有的數據集來自SPMF數據庫［19］。

Bible是稠密數據集，它包含36 369個序列和13 905個不同項目。Kosarak10k是稀疏數據集，它包含了從一個匈牙利新聞門戶網站收集的10 000個點擊流數據序列。Chess數據集和Retail數據集都是具有合成效用值的真實數據集。Chess數據集是稠密數據集，Retail數據集是高度稀疏的數據集。

3.2 增量挖掘結果的準確性

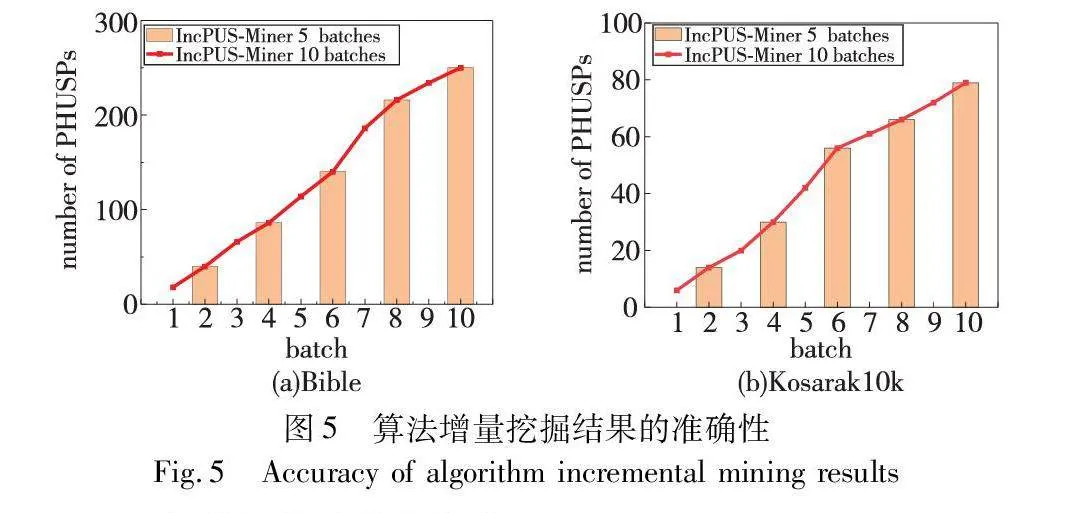
本節對IncPUS-Miner算法增量挖掘的準確性進行了實驗。選擇了稠密數據集Bible和稀疏數據集Kosarak10k，minutil分別設置為100 000和10 000，其余參數設為固定值（maxPer=100，maxAvg=20，minPer=minAvg=1）。

在實驗中，每個數據集被分為5批、10批。IncPUS-Miner算法的挖掘結果如圖5所示。可以看出，隨著批次的加入，算法發現的PHUSPs數量也在增加，且相同數據集在不同批次下挖掘模式的最終數量是相等的。因此，IncPUS-Miner算法可以有效地處理增量數據，逐步挖掘所有PHUSPs。

3.3 所提剪枝策略的有效性

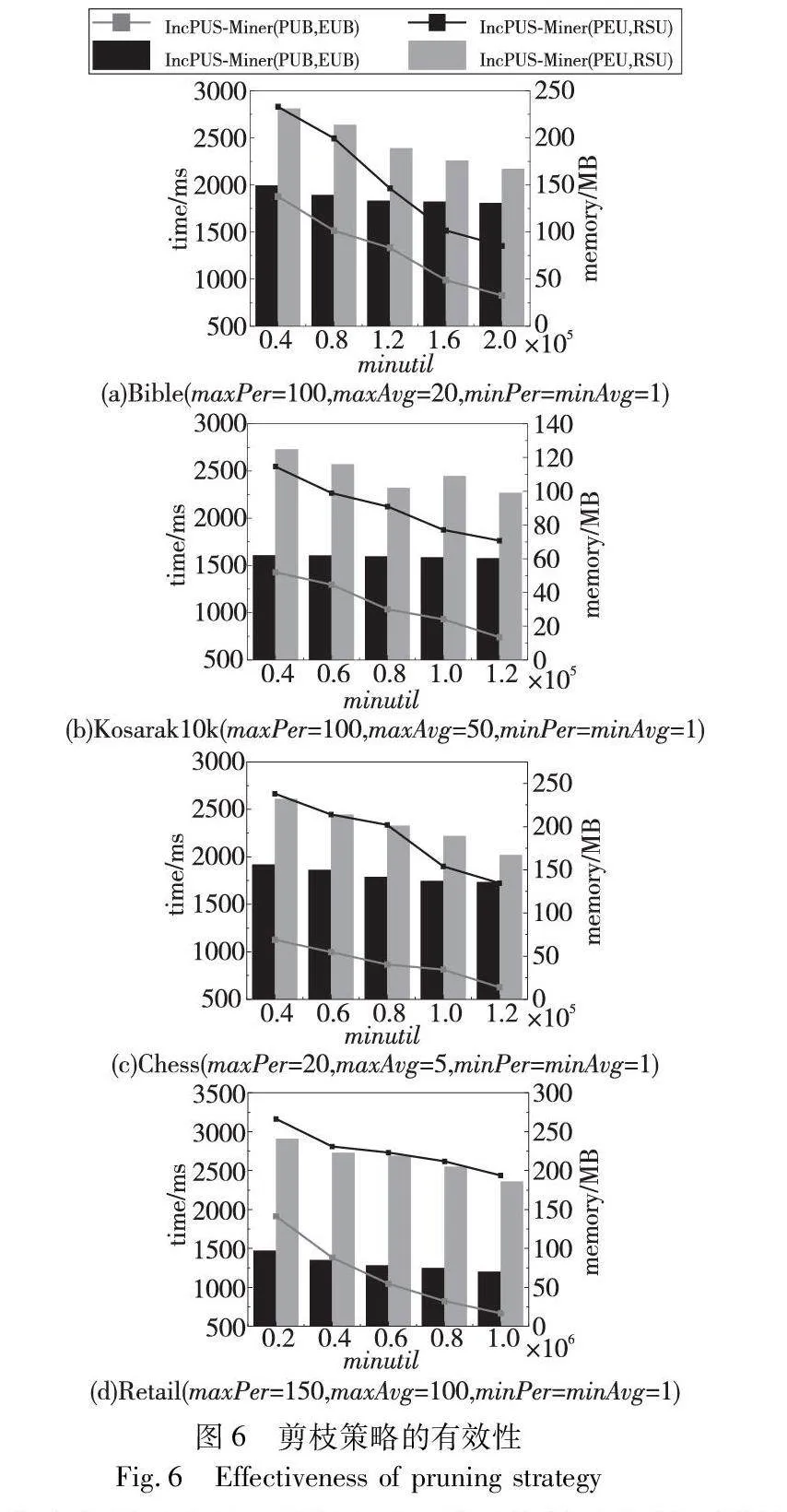
本組實驗將提出的兩個新的效用上界（PUB，EUB）與前人提出的上界（PEU，RSU）［10］進行對比，以評估其在模式挖掘中的性能。采用四個真實數據集進行實驗，以確保比較的全面性和可靠性，如圖6所示。由于剪枝策略是針對模式效用提出的，故將最小效用閾值（minutil）作為X軸，挖掘過程中算法的運行時間與內存占用情況作為Y軸。通過分析實驗結果，應用所提剪枝策略的IncPUS-Miner算法在運行時間和內存占用方面都優于應用傳統效用上界的IncPUS-Miner算法。因此，所提的剪枝策略可以有效減少算法搜索空間，節省時間與內存消耗。

3.4 參數對算法的影響及算法性能評估

在實際應用中，為了合理設置IncPUS-Miner相關參數，需考慮數據集特征和研究問題需求。在3.4.1節和3.4.2節中分別評估了參數minutil和maxPer對算法性能的影響。

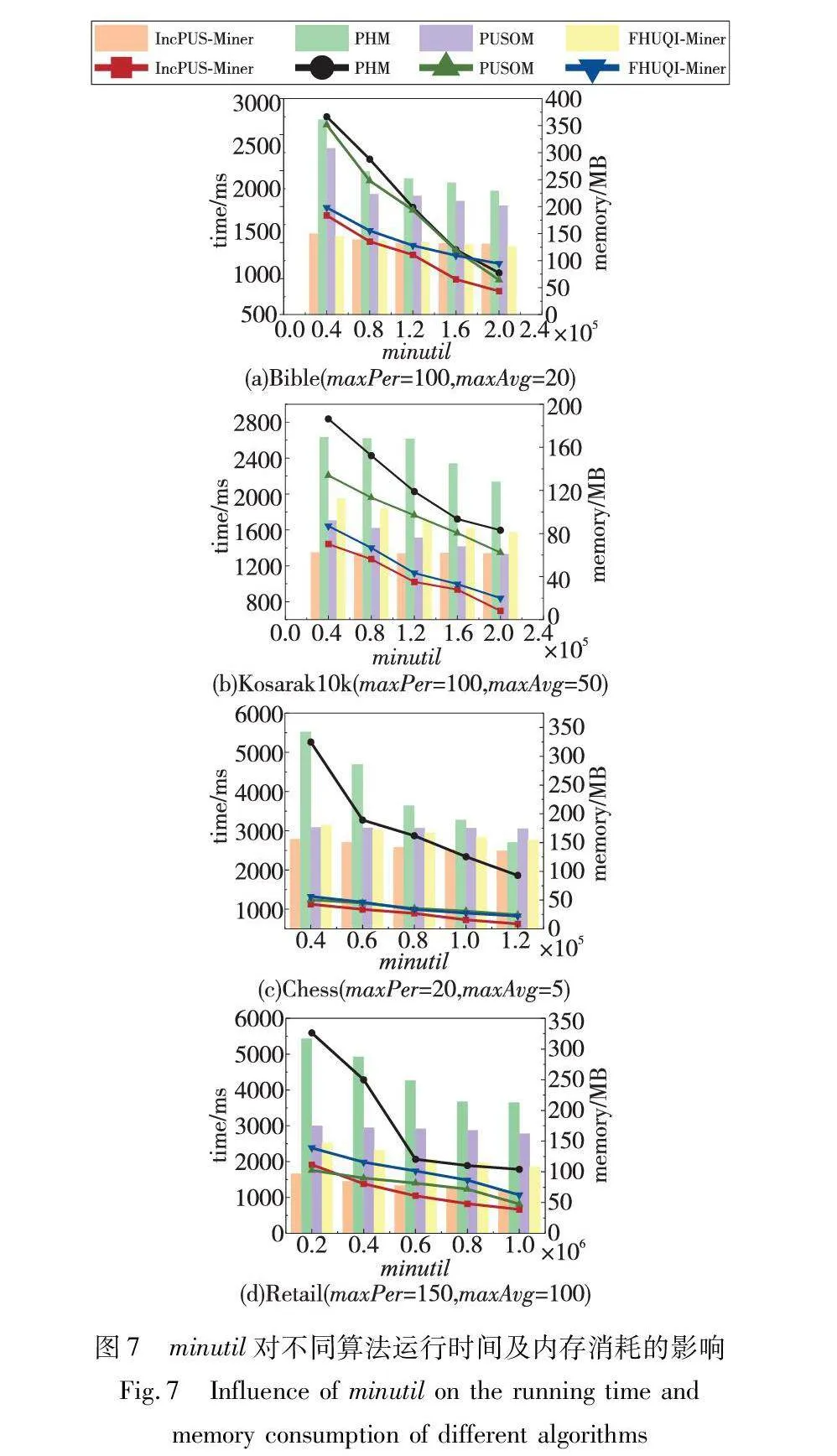
3.4.1 minutil對算法效率的影響

本組實驗旨在通過對每個數據集設置不同的最小效用閾值（即minutil）來評估算法的性能。實驗將IncPUS-Miner算法與三個對比算法在數據集上進行比較，并將參數minPer和minAvg設置為1，剩余參數maxPer和maxAvg在每個數據集都設定為經驗值，具體數值在圖7中體現。

通過分析圖7發現，隨著最小效用閾值的增加，滿足條件的項集逐漸減少，導致算法的運行時間下降。值得注意的是，IncPUS-Miner算法在所有情況下的運行時間均低于其他對比算法，這得益于提出的pu-tree結構和剪枝策略，它們共同作用有效提高了挖掘效率。pu-tree結構使算法能夠更快速且精準地定位潛在高效項目集，而剪枝策略則進一步減少了搜索空間，從而降低了計算成本。這兩個因素共同確保了IncPUS-Miner在不同最小效用閾值下都能取得較快的運行速度。

與靜態挖掘PHUSPs算法相比，增量挖掘PHUSPs需要考慮新添加的事務，這更為復雜。通過比較四種算法在內存使用方面的性能可以看出，IncPUS-Miner算法比其他三種算法消耗更少的內存。在密集數據集中的PHUSPs數量相對較大，會生成更多的候選項集。因此，IncPUS-Miner算法在稀疏數據集上有更好的效果。

實驗結果表明，IncPUS-Miner算法在處理各種數據集時都表現出優越的性能，可以有效地逐步挖掘PHUSPs。

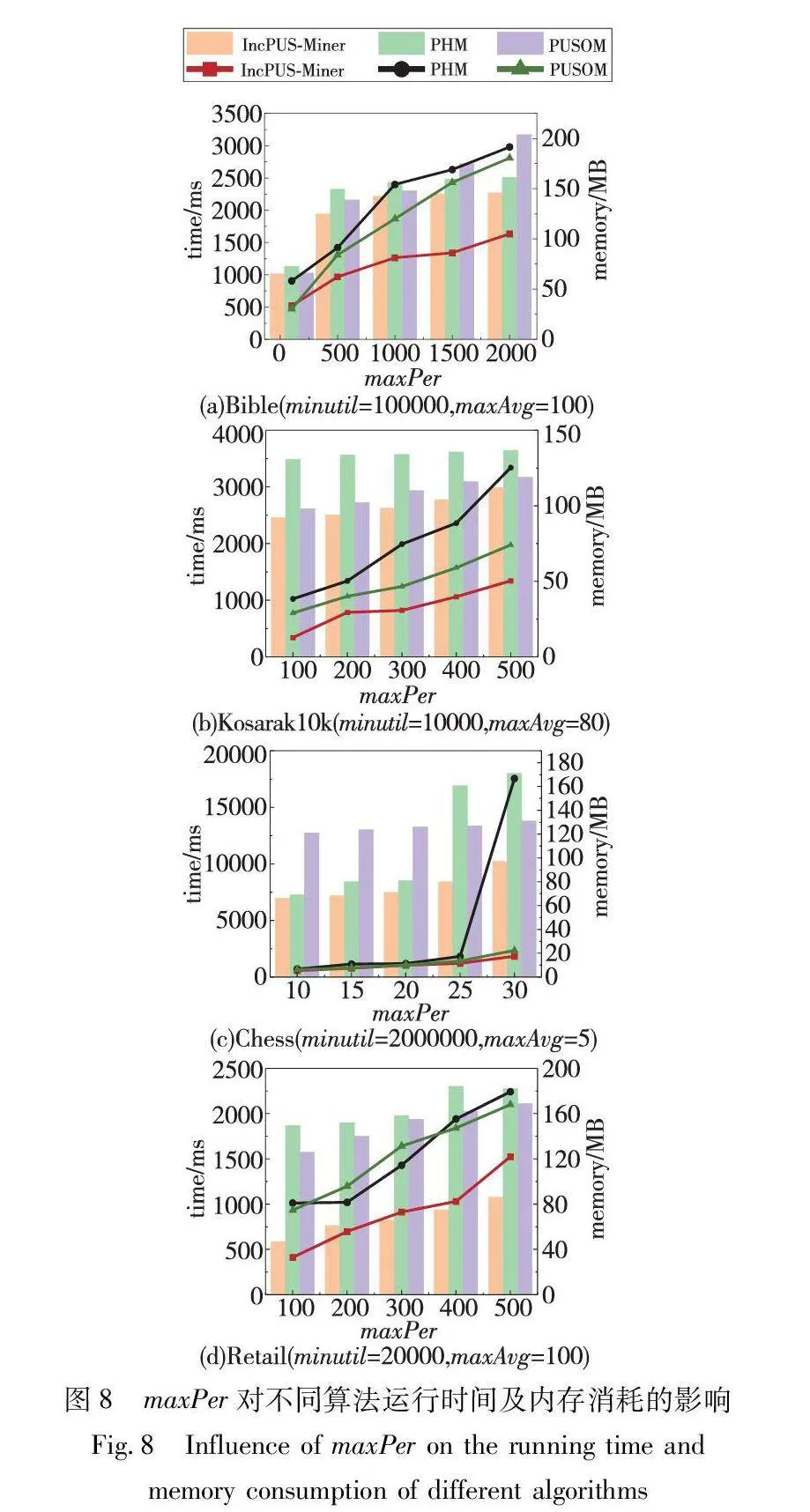
3.4.2 maxPer對算法效率的影響

本組實驗研究了最大周期閾值（maxPer）對算法性能產生的影響。由于參數maxPer對FHUQI- Miner算法沒有影響，實驗只對比了PHM、PUSOM和IncPUS-Miner三種算法，并記錄了它們在不同maxPer值下的運行時間與內存消耗情況。在圖8中呈現的實驗結果可知，隨著maxPer值的增加，所有算法的運行時間和內存消耗均呈上升趨勢。這是因為隨著maxPer值的增大，滿足周期性的高效用模式數量也隨之增加，使得算法需要處理更多的模式，因而在執行過程中消耗更多的計算資源和內存空間。對于特定問題場景，通過合理設置maxPer值，可以在滿足性能需求的同時減少不必要的計算負擔。

通過比較不同算法的性能變化情況可以看出，IncPUS-Miner算法在各個maxPer值下表現出明顯的優勢。具體而言，相對于其他兩種算法，IncPUS-Miner算法在高maxPer值情境下的運行時間和內存消耗增長更為緩慢，這表明該算法在處理大規模周期模式的數據時具有更強的適應性。

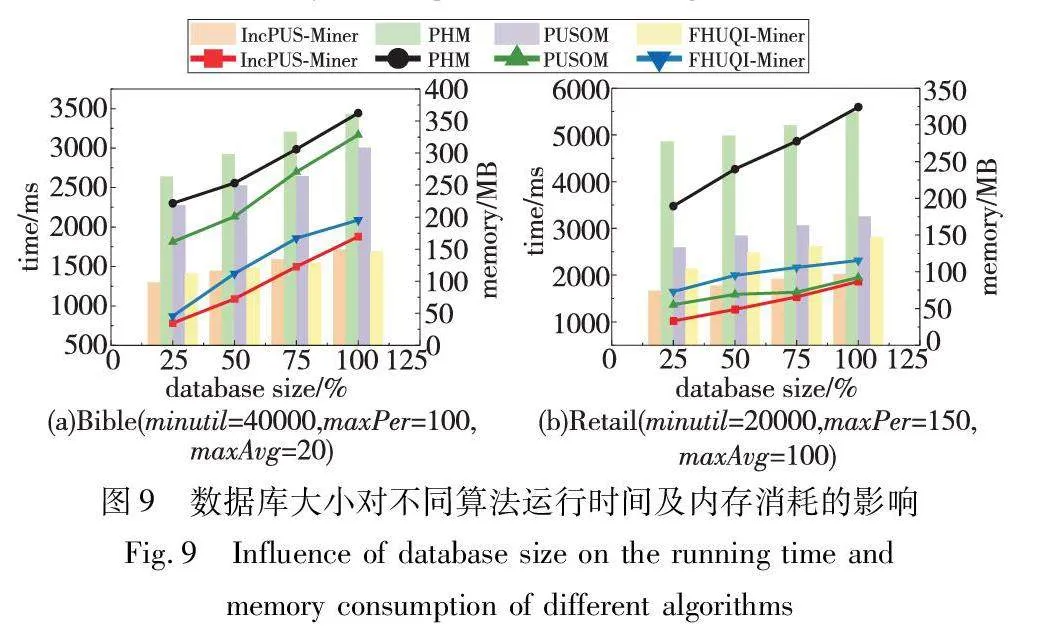
3.5 可擴展性

該組實驗選擇數據集Bible和Retail評估了數據庫大小及增量數據對IncPUS-Miner算法整體性能的影響。依據上述實驗，將參數minPer和minAvg固定設置為1，并以25%的增量改變數據庫的大小，比較了四種算法在運行時間和內存消耗方面的性能，實驗結果如圖9所示。從圖9可以看出，PHM算法在數據集上的運行時間和內存消耗明顯高于其他四種算法。這是因為PHM算法采用的事務加權利用率（TWU）度量較為寬泛，使得算法需要處理更多的候選模式。另外，該算法在處理新數據時需要重新從頭開始挖掘模式，進一步增加了運行時間和內存消耗的負擔。因此， PHM算法在處理增量數據挖掘任務時顯得不夠適用。與之相對，IncPUS-Miner算法在逐漸增大的序列數據集中展現出更為優越的性能。這是因為IncPUS-Miner算法采用的pu-tree結構在處理增量數據時不僅可以有效地維護和更新模式的信息，而且能夠支持算法在增量情境下的高效運行；其次，算法采用的剪枝策略可以有效減少冗余計算，隨著數據集規模的增大，該剪枝策略能夠精確地確定哪些模式是無用的，從而更早地進行剪枝，減少候選模式的數量，提高了算法在挖掘過程中的效率。

4 基因序列應用分析

在生物醫學領域中，考慮到一些基因在特定疾病中的重要性以及在生物治療下的時間特性，通過PHUSPM分析有助于識別在特定疾病的發病機制中重要的基因調控序列模式。

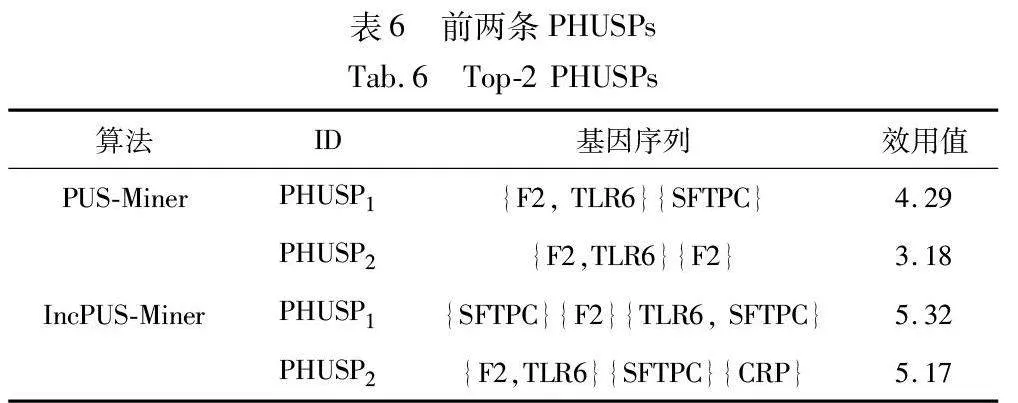
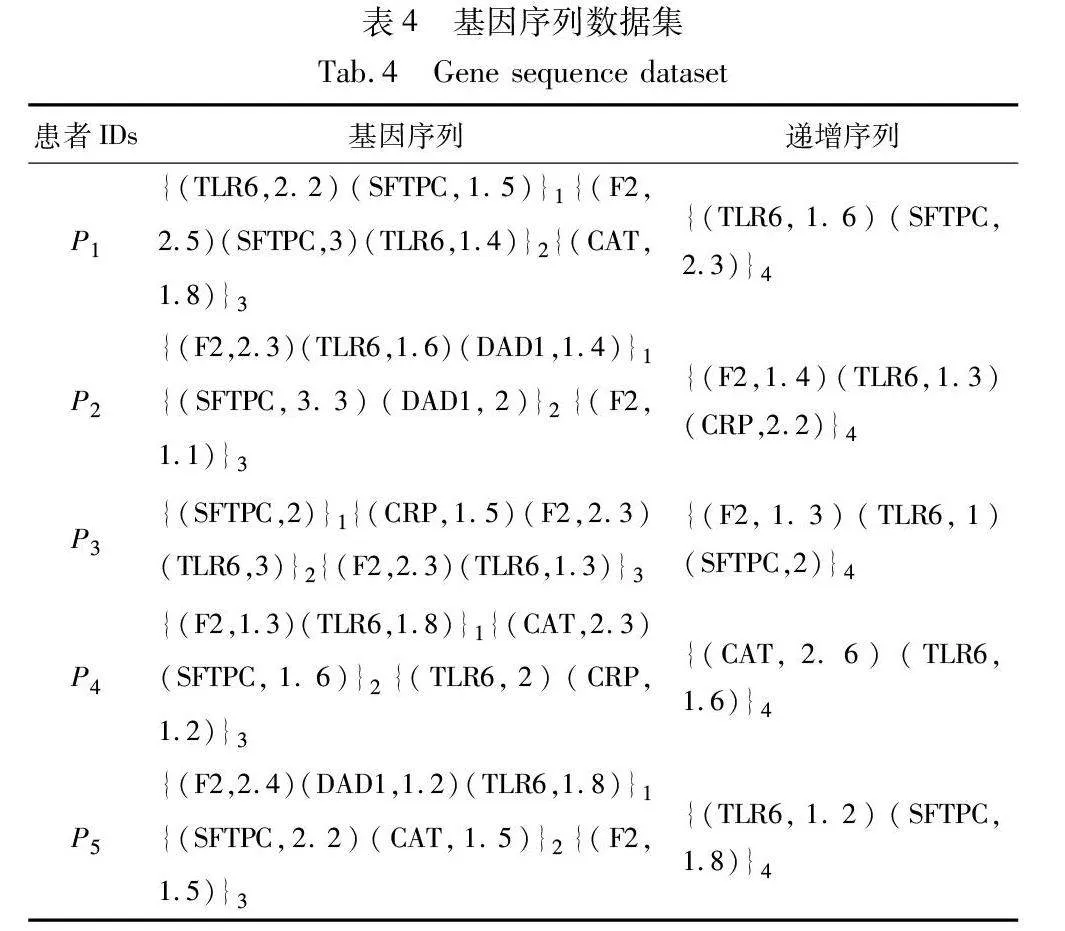
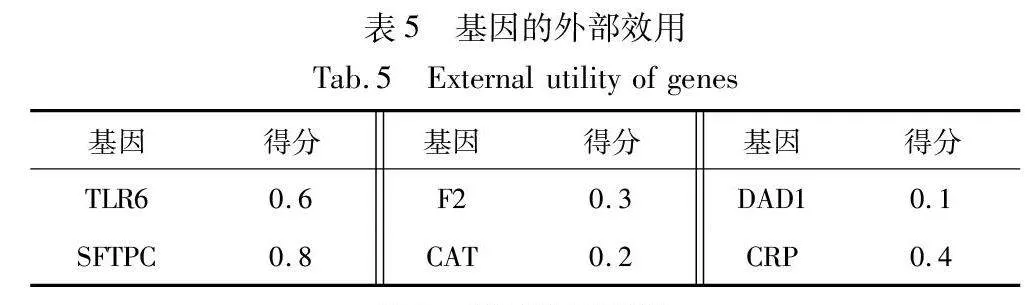
表4呈現了一個基因序列數據集的實例。第一列標識了六個肺炎患者的ID，其余列提供了在TP1、TP2、TP3、TP4這四個時間點上七種基因的基因表達值（內部效用）。基因的外部效用應該代表基因對引發肺炎的重要性，這里使用DisGeNET提出的基因-疾病關聯評分（score）作為每個基因的外部效用，如表5所示。通過PUS-Miner和IncPUS-Miner算法進行挖掘分析，提取挖掘結果中的前兩條PHUSPs記錄在表6中。

觀察表6的挖掘結果發現，IncPUS-Miner算法能夠及時捕捉到新的基因調控模式，這些模式很可能與肺炎的發生和發展密切相關。隨著病患者基因數據的積累，該算法允許實時更新模型，能夠實時挖掘出在不同階段的肺炎中起關鍵作用的基因調控序列，從而更全面地理解基因在特定疾病發病機制中的作用。從總體結果來看，該算法能夠更有效地探索基因與疾病之間的關系，為生物醫學領域數據分析提供了有益的工具。

5 結束語

針對PHUSPs的增量挖掘問題，設計了一種高效的算法IncPUS-Miner。IncPUS-Miner算法依賴于pu-tree結構和更新效用列表（UUL）來促進增量挖掘過程。pu-tree結構可以有效處理新數據，UUL用來存儲簡潔的輔助信息，以消除冗余計算，提高算法整體效率。此外，還介紹了兩個新的序列效用上界以及對應的剪枝策略，有助于更準確地確定無用模式，并在挖掘過程中更早地進行剪枝，從而減少執行時間和內存使用。實驗結果表明，IncPUS-Miner算法可以有效地從增量數據庫中挖掘PHUSPs，且在執行時間和內存使用方面優于其他算法，該算法為解決PHUSPs的增量挖掘問題提供了可靠且高效的解決方案，為應對資源有限性的實際應用場景提供了顯著的優勢。未來研究將專注于自適應策略，通過智能調整算法參數，更好地適應不同數據分布的變化，從而提升算法在實時環境中的性能表現。

參考文獻：

［1］Fournier-Viger P， Lin J C W， Kiran R U， et al. A survey of sequential pattern mining［J］. Data Science and Pattern Recognition， 2017，1（1）： 54-77.

［2］吳軍， 歐陽艾嘉， 張琳. 基于標準置換檢驗的差異序列模式挖掘算法［J］. 計算機應用研究， 2021， 38（3）： 710-713. （Wu Jun， Ouyang Aijia， Zhang Lin. Mining discriminative sequential patterns based on standard permutation testing［J］. Application Research of Computers， 2021， 38（3）： 710-713.）

［3］Gan Wensheng， Lin J C W， Zhang Jiexiong， et al. Fast utility mining on sequence data［J］. IEEE Trans on Cybernetics， 2021，51（2）： 487-500.

［4］Ahmed C F， Tanbeer S K， Jeong B S. A novel approach for mining high-utility sequential patterns in sequence databases［J］. ETRI Journal， 2010，32（5）： 676-686.

［5］Wang Junzhe， Huang J L， Chen Yicheng. On efficiently mining high utility sequential patterns［J］. Knowledge & Information Systems， 2016， 49（2）： 597-627.

［6］Han Meng， Shan Zhihui， Han Qiang. Incrementally updating high utility quantitative itemsets mining algorithm［J］. Journal of Intelligent & Fuzzy Systems， 2022， 43： 2435-2448.

［7］Yun U， Nam H， Lee G， et al. Efficient approach for incremental high utility pattern mining with indexed list structure［J］. Future Generation Computer Systems， 2019， 95： 221-239.

［8］Kim D， Yun U. Efficient algorithm for mining high average utility itemsets in incremental transaction databases［J］. Applied Intelligence， 2017， 47（1）： 114-131.

［9］Wang Junzhe， Huang J L. Incremental mining of high utility sequential patterns in incremental databases［C］//Proc of the 25th ACM International on Conference on Information and Knowledge Management. New York： ACM Press， 2016： 2341-2346.

［10］毛伊敏， 鄧千虎， 鄧小鴻， 等. 改進的并行關聯規則增量挖掘算法［J］. 計算機應用研究， 2021，38（10）： 2974-2980. （Mao Yimin， Deng Qianhu， Deng Xiaohong， et al. Improved parallel association rules incremental mining algorithm［J］. Application Research of Computers， 2021， 38（10）： 2974-2980.）

［11］Yun U， Ryang H， Lee G， et al. An efficient algorithm for mining high utility patterns from incremental databases with one database scan［J］. Knowledge-Based Systems， 2017， 124： 188-206.

［12］Wang Junzhe， Huang Jiunlong. On incremental high utility sequential pattern mining［J］. ACM Trans on Intelligent Systems and Technology， 2018， 9（5）： 1-26.

［13］Dinh T， Huynh V N， Le B. Mining periodic high utility sequential patterns［C］//Proc of Asian Conference on Intelligent Information and Database Systems. Cham： Springer， 2017： 545-555.

［14］Xie Shiyong， Zhao Long. An efficient algorithm for mining stable periodic high-utility sequential patterns［J］. Symmetry， 2022， 14（10）： 2032.

［15］Zihayat M， Davoudi H， An A. Top-k utility-based gene regulation sequential pattern discovery［C］//Proc of IEEE International Confe-rence on Bioinformatics and Biomedicine. Piscataway，NJ： IEEE Press， 2016： 266-273.

［16］Fournier-Viger P， Lin J C W， Duong Q H， et al. PHM： mining perio-dic high-utility itemsets［M］//Perner P.Advances in Data Mining. Cham： Springer， 2016： 64-79.

［17］Dinh D T， Le B， Fournier-Viger P， et al. An efficient algorithm for mining periodic high-utility sequential patterns［J］. Applied Intelligence， 2018， 48（12）： 4694-4714.

［18］Nouioua M， Fournier-Viger P， Wu C W， et al. FHUQI-Miner： fast high utility quantitative itemset mining［J］. Applied Intelligence， 2021， 51： 6785-6809.

［19］Fournier-Viger P， Gomariz A， Gueniche T， et al. SPMF： a Java open-source pattern mining library［J］. The Journal of Machine Learning Research， 2014，15（1）： 3389-3393.