數學文化在高中數學教學中的滲透策略


[摘要] 數學家、數學符號、數學思想、數學之美等皆屬于數學文化。新課標明確了數學文化的價值,在高中數學教學中滲透數學文化為創新教學方式提供了新思路。本文論述了在高中數學教學中滲透數學文化的必要性,并結合湘教版高中數學必修一第1章“集合”的教學實踐,探索數學文化在高中數學教學中的有效滲透路徑,讓學生從另一種角度認識數學知識的本質。
[關鍵詞] 數學文化;高中數學;滲透策略
數學文化中既有數學家的奇聞逸事,也有數學史的發展進程,還有豐富的數學思想和成果。“體現數學的文化價值”是《普通高中數學課程標準(2017年版2020年修訂)》(以下簡稱“新課標”)的基本理念之一,新課標提出了在教學內容中融入數學文化的學習要求。數學文化的價值體現在數學學科的工具性特征中,如解決問題時所應用的數學思想;也表現在數學學科的文化引領作用上,如幾何知識的美學特征。在高中數學教學中,有效滲透數學文化,突破“知識本位”,將教學上升至一個新的高度,能夠起到拓寬學生知識面、培養學生數學核心素養的作用。本文選擇湘教版高中數學必修一第1章“集合”作為滲透數學文化的載體,引導學生探索集合論的起源,讓學生了解數學家康托爾從實際問題中抽象出“集合”這一概念的歷程,全面認識“集合”這一數學分支的發展過程。
一、在數學教學中滲透數學文化的必要性
數學是一門精確的科學,蘊含著豐富的文化內涵。在高中數學教學中滲透數學文化,既是向學生傳遞數學知識和技能的需要,也是促進學生思維發展和精神追求的需要。數學文化帶有科普意味,既有嚴謹性,也有趣味性,像故事一樣吸引學生讀下去。湘教版高中數學必修一第1章“集合”就有“數學文化”板塊,向學生介紹了與“邏輯與集合”相關的數學文化知識,包括數學中的邏輯起源、集合論的誕生與發展等。通過滲透數學文化,幫助學生深入理解數學抽象、邏輯推理、直觀想象的內涵和應用,有助于提高學生的數學綜合能力,符合新課標培養學生數學核心素養的要求。
教材中,除了專門設置“數學文化”板塊外,還將一些例題和習題放在了數學文化的背景下,引導學生運用所學知識解決實際問題,感受數學的魅力。因此,教師在教學過b3d9c9ea34f283d5a25c12df377c01a5a3bbf7f7cfb680032e9976168e5871a8程中要充分利用數學文化資源,向學生講述數學家的故事,講解數學史話,使數學文化成為教學知識點的有效補充和延伸,讓學生了解數學的發展歷程和數學家的探索精神,培養學生的科學素養和人文精神。
二、高中數學教學中滲透數學文化的有效路徑
“集合”是很多版本高中數學教材的第一章內容,集合的思想與方法開啟了學生的高中數學學習。基于數字文化視角開展教學,教師通過巧妙導入,喚醒學生已有的認知,帶領學生認識“集合論之父”康托爾,了解集合符號,探尋圖形語言,感悟集合論形成的精神,在“集合”的學習中真正注入數學文化元素。
1.巧妙導入喚醒認知,聯結新舊知識
高中數學相較初中數學而言,知識難度普遍加大了,教學內容范圍也更寬了,但高中數學學習都以初中數學知識為支撐,初、高中數學之間存在緊密的聯系。對于實際的教學,教師直接開講雖然能節省時間,較快地完成教學任務,但是學生不易理解知識,常常處于被動接受的狀態。為此,教師要分析學情,充分考慮學生的具體情況,在新知導入環節聯結初中數學的舊知識點,以此調動學生已有的學習經驗,在新舊知識聯結中讓學生理解所學內容。
結合以往教學經驗,許多學生認為集合的概念高度抽象,難以理解。其實,在初中階段的部分內容就已經或多或少地涉及“集合”,教師在新課導入環節可帶領學生回顧初中相關知識點。初中時學生已經學了“解的集合”,教師在課堂教學之初可以先列出若干一元一次方程習題,要求學生按照正確步驟,求解未知數,得到解的集合。教師將解集的概念和性質與本課所學集合的概念、集合元素的特征進行對比,借助對應、類比的數學思想,幫助學生聯結舊知、消化新知,實現初中數學向高中數學的“無痕”過渡。
集合論的創立對于數學學科的發展意義重大,“集合”這一章內容之所以被放在各版本高中數學教材的第一章,是因為集合既能承接初中階段所學的方程、不等式等知識內容,也是接下來學習高中數學函數、解析幾何、概率統計等知識的基礎。可以說,集合是教學重點,是數學思想方法,是數學文化的重要內容。教師通過聯結新舊知識,引導學生巧妙運用集合的知識與思想方法,讓學生打牢高中數學學習的基礎。
2.認識“集合論之父”,激發學習興趣
集合論對現代數學有奠基作用,作為高中數學的最開始的學習內容,“集合”這一章有著抽象的概念和獨特的算法。學生要想學好高中數學,首先就要跨過“集合”這一關。提起“集合”就不得不提一個名字,他就是集合論的創立者——康托爾。為了避免學生一上來就被集合抽象的概念和多樣的表示方法“嚇到”,教師可以從康托爾的生平事跡入手,以講故事的形式吸引學生注意力,激發學生對集合的學習興趣。
通過播放微視頻資料,學生直觀地了解康托爾的生平事跡,特別是與集合論創立的相關內容。康托爾從小就表現出對數學的興趣,獲得家人支持后,輾轉多地求學,義無反顧地投入數學研究工作,此后畢生都致力于集合論和超窮數理論的研究。學生通過了解康托爾的生平事跡,對集合論的誕生有了初步的了解。在此過程中,有的學生可能發現集合論一開始并沒有得到認可,這種反對聲音與康托爾提出的一些假設存在矛盾。此時,教師可以抓住這個寶貴的教學時機,融入“羅素悖論”,即“理發師悖論”,讓學生看到集合論艱難的發展進程。“羅素悖論”指出,如果所有的理發師都給自己理發,就會出現一個理發師既給自己理發又不給自己理發的情況,這顯然是自相矛盾的。而且,這個悖論對康托爾集合論產生了深遠的影響,引發了數學界長達數十年的爭議和探討。這樣的教學不僅能讓學生了解集合論的誕生背景,而且能讓學生體會數學理論發展的曲折歷程。有了數學文化的滲透,學生認識到,今天在課堂上學習的都是前人奮斗一生凝練的思想和方法,自己是站在數學巨人的肩膀上學習新知,這樣的教學有助于調動學生學習的積極性。
3.感受集合符號之美,譜寫數學樂章
數學符號是數學文化的重要體現,小小的數學符號既是藝術的創造,又是智慧的結晶。有的數學符號是偶然得之,但更多的數學符號發明的背后都有一段有趣的歷史。從最初簡單的數學符號到越來越復雜的數學符號,代表著數學的發展史,也是人類思維不斷躍遷的印證。“集合”這一章的教學涉及非常多的數學符號,許多數學符號對于學生來說是陌生的,而部分教師在教學中往往對數學符號的作用“視而不見”,這無疑是對數學文化資源的浪費,也錯失了良好的育人機會。
集合間的關系與運算是“集合”這一章的教學重點,學生要學到子集關系、相等關系、真子集關系、交集運算、并集運算等知識點,集合間的關系與運算都能用相應的數學符號進行表示,集合符號之多也成為一部分學生認為集合難學的因素之一。因此,對于集合符號,教師不能一句帶過,有必要帶領學生認識集合符號的來歷,讓學生真正認識集合符號,在集合符號中看到人類的創造力和數學之美。比如,在學習并集符號“∪”、交集符號“∩”時,教師除了向學生解釋符號表示的意義外,還可以從“∪”和“∩”作為“廢物”被再次利用這一趣聞軼事談起,讓學生了解數學符號的前世今生。
在記憶集合符號時,教師可以從“∪”對應的英文單詞“Universe”有“全”的意思來幫助學生聯系“并”集。學生記住了并集,也就不會將其與交集混淆了。除了常規方法外,教師還可以讓學生“大開腦洞”,用形象的方法來記憶集合符號(如圖1)。在記憶集合名和符號的時候,也不能死記硬背,教師指導學生用表格來整理不同的集合名和表示符號(如表1),讓集合符號“集合”起來,促進學生的理解和記憶。
4.探尋集合圖像之源,形成應用意識
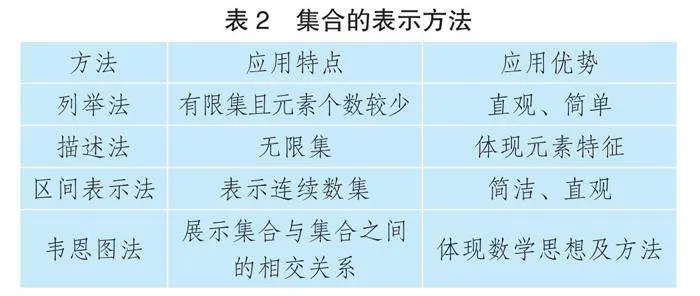
集合有多種表示方法(如表2),不同的表示方法有不同的應用特點和優勢。其中韋恩圖法是利用封閉曲線來表示集合的一種方法,能體現數形結合的思想方法。教材中對于韋恩圖的體現并不多,為了使學生更好地掌握用圖形表示集合的方法,教師在集合教學時可以與學生溯源圖形語言,從最初的歐拉圖雛形,到后來邏輯學家韋恩的改進,再到麥克沙恩明確其定義,探尋韋恩圖的起源和發展,使數學課堂更具探索意味。
為了便于學生對數學思想和方法的掌握,可以從滲透數學文化入手,通過應用練習拓展,深化學生對韋恩圖法的掌握。比如,教師引導學生對教材第12頁第13題“關于訂閱不同報紙相關問題”進行變式練習,以提高學生的實際應用能力。
5.認識集合發展之路,培養探究精神
康托爾說過:“數學的本質在于它的自由。”但是,這位數學家卻沒有數學的本質那般自由,他的一生是偉大的,也是令人唏噓的。說康托爾的一生是偉大的,是因為他的集合論被認為是人類純粹智力活動的最高成就之一。說康托爾的一生是令人唏噓的,是因為他的研究在很長時間遭人質疑,他也一直生活在巨大的精神壓力之下,并飽受精神分裂和抑郁癥的困擾。
1897年,第一屆國際數學家大會上康托爾創立的集合論才得到公開承認,這時距離1874年康托爾發表的《關于一切代數實數的一個性質的論文》已過去
13年。教材中“數學文化”板塊中提到“著名數學家龐加萊和康托爾的老師克羅內克都對康托爾進行非難和指責,雙方的爭辯持續了十年之久”。可以想象康托爾在當時面對的是何種困境,但是他勇于探究以往數學家不敢闖入的未知領域,這正是數學學習過程中彌足珍貴的探究精神。教師以康托爾的探索精神作為課堂教學末段的升華,引導學生學習并發揚這種偉大的探索精神,在高中數學的“海洋”中努力收獲屬于自己的成果。
綜上所述,高中數學教學不應被各種定理、公式和習題填滿,還應通過滲透數學文化,激發學生數學學習的興趣,幫助學生理解數學的本質。在高中數學教學中教師要有意識地滲透數學文化,找準數學文化融入數學教學的契合點,在理性與人文的有機結合中提升學生的數學核心素養。
[參考文獻]
[1]高原.數學文化與高中數學教學結合的對策分析[J].數理天地(高中版),2023(19):53-55.
[2]吳金炳.數學文化在高中數學教學中的滲透策略探究[J].數學學習與研究,2022(27):113-115.
[3]汪曉勤.中華優秀傳統數學文化融入高中數學教學的若干路徑[J].教育研究與評論(中學教育教學),2022(09):27-34.

