“雙減”視域下初三總復(fù)習(xí)大單元教學(xué)設(shè)計實踐與思考

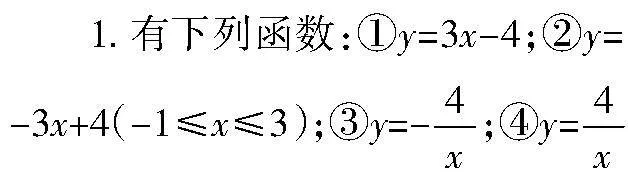
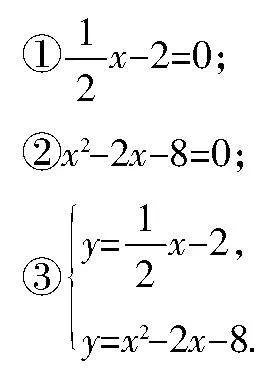
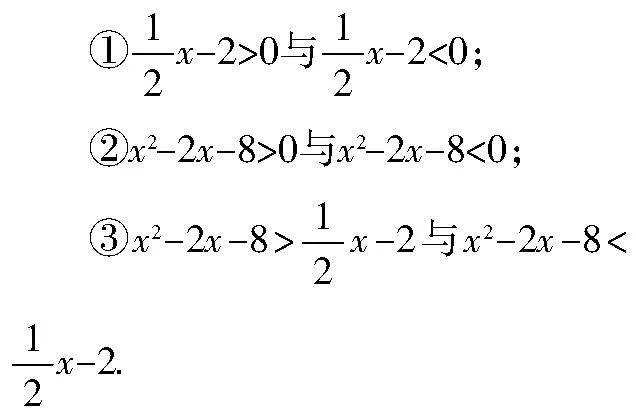
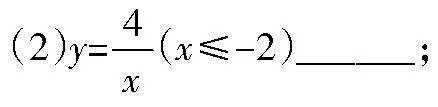
[摘 要] “雙減”背景下，如何保證不同層次學(xué)生通過合理、科學(xué)的學(xué)習(xí)提升自己的學(xué)習(xí)能力，提升數(shù)學(xué)素養(yǎng)，是對一線教師的一大考驗. 針對初三學(xué)生，實施大單元復(fù)習(xí)課教學(xué)，以學(xué)生為主體，以知識為載體，可以達到梳理知識體系、鞏固基礎(chǔ)知識和基本技能，提升學(xué)生思維，培養(yǎng)學(xué)生核心素養(yǎng)的目標.

[關(guān)鍵詞] 大單元教學(xué);實踐;類型

“雙減”背景下，學(xué)生的學(xué)習(xí)壓力得到進一步緩解，學(xué)習(xí)能力在分層教學(xué)理念指導(dǎo)下得到進一步提升. 在“雙減”精神指導(dǎo)下，如何保證不同層次學(xué)生通過合理、科學(xué)的學(xué)習(xí)提升自己的學(xué)習(xí)能力，提升數(shù)學(xué)素養(yǎng)，是我們一線教師面臨的一大挑戰(zhàn). 對于初三教師來說，時間緊、任務(wù)重，面對中考，如何以學(xué)生為主體，以知識為載體，以訓(xùn)練學(xué)生思維、培養(yǎng)學(xué)生核心素養(yǎng)為目標，值得我們一線教師思考. 基于此，我們可以考慮采用大單元教學(xué)復(fù)習(xí)的手段，以此系統(tǒng)建構(gòu)學(xué)生的認知結(jié)構(gòu)，從而提升學(xué)生的思維水平，達到事半功倍的效果.

大單元教學(xué)的定義

所謂大單元教學(xué)設(shè)計，是指教師從整體角度出發(fā)，從數(shù)學(xué)知識主線、學(xué)生認知規(guī)律、教學(xué)組織原則等方面，將教材中具有某種關(guān)聯(lián)性的內(nèi)容進行分析、重組、整合，以優(yōu)化教學(xué)效果的一種教學(xué)設(shè)計.

大單元教學(xué)的類型

（一）以核心知識為線索的知識類

以核心知識為線索的知識類大單元教學(xué)，可以洞悉知識的來龍去脈，建立知識之間的本質(zhì)聯(lián)系，并強化對數(shù)學(xué)知識結(jié)構(gòu)的整體認識[1]，促進知識間的融會貫通，從而統(tǒng)籌重組，形成知識類主題. 筆者認為，這就是按照學(xué)科內(nèi)容進行“大整合”，把相關(guān)聯(lián)的知識放在一起，以“大學(xué)科”的視角進行歸類. 這也是我們在進行大單元教學(xué)時常用的方法.

（二）以數(shù)學(xué)方法為線索的方法類

采取這種方式，可以把看似無關(guān)的零散知識點通過思維方法的分析有機地串聯(lián)在一起，強化這些知識間的聯(lián)系，形成方法類主題[1]，促進學(xué)生思維橫向貫通.

筆者認為，這就是按照思想方法進行“大遷移”，這種方式跨越了學(xué)年的界限，能促進學(xué)生思維實現(xiàn)“由點及面”的遷移.

（三）以核心素養(yǎng)為線索的素養(yǎng)類

通過這種方式，選擇數(shù)學(xué)抽象、邏輯推理、數(shù)學(xué)建模、數(shù)學(xué)運算、直觀想象、數(shù)據(jù)分析等核心素養(yǎng)進行專題設(shè)計. 通過注重載體、素養(yǎng)進階，形成素養(yǎng)類主題. 筆者認為，這就是按照核心素養(yǎng)實現(xiàn)“大貫通”，這種方式以核心素養(yǎng)為主題，通過教師“反芻”，學(xué)生“自主消化”，最終轉(zhuǎn)化成學(xué)生的個人能力.

數(shù)學(xué)思想方法是數(shù)學(xué)知識的提煉與升華，數(shù)學(xué)核心素養(yǎng)是基于數(shù)學(xué)思想、參與數(shù)學(xué)活動、做出數(shù)學(xué)判斷的必備能力. 通過以上分析我們可以發(fā)現(xiàn)，三種大單元教學(xué)類型并不是并列的，而是基于學(xué)生的思維發(fā)展“最近發(fā)展區(qū)”來劃分的，所以教師教學(xué)時應(yīng)根據(jù)學(xué)情采用合適的類型.

大單元教學(xué)的意義

一方面， 多數(shù)教師在進行初三復(fù)習(xí)時，采用的仍然是教科書的形式，以單個、孤立的知識呈現(xiàn)，使學(xué)生對于知識的習(xí)得呈現(xiàn)碎片化的形式，忽視了數(shù)學(xué)知識本來就是一個有機的統(tǒng)一體，這樣學(xué)生很難把知識聯(lián)系起來. 另一方面，教師只注重學(xué)生知識的運用，忽視了知識的積累路徑，以致學(xué)生不能將相關(guān)聯(lián)的知識串聯(lián)起來，不利于學(xué)生系統(tǒng)地掌握數(shù)學(xué)知識，形成一棵“知識樹”，導(dǎo)致學(xué)生遷移能力不強，學(xué)習(xí)效率低下. 大單元教學(xué)則能夠規(guī)避以上問題，一方面使得學(xué)生在知識習(xí)得的連續(xù)性、邏輯思維發(fā)t2PomOF+cdEQXNPdxClnfstzEbX3GJ3XE/GKMtlVrrI=展的嚴密性上獲得不斷提升，能夠關(guān)注知識生成的連續(xù)性和過程性，最后內(nèi)化為個人的能力;另一方面，也使得教師的關(guān)注點從基礎(chǔ)知識、基本技能、基本思想方法，到課程的發(fā)展和個人能力的提升，最終促進教師專業(yè)功底的提高[2].

大單元教學(xué)的教學(xué)示例

復(fù)習(xí)課作為一種常態(tài)課型，具有梳理知識體系、鞏固基礎(chǔ)知識和基本技能、提煉一般方法、總結(jié)經(jīng)驗技巧的功能[2]. 如何在“雙減”背景下實施大單元復(fù)習(xí)課教學(xué)呢？筆者以初中數(shù)學(xué)“函數(shù)、方程、不等式”為例，實施大單元復(fù)習(xí)課教學(xué)[3].

（一）自查

⑤y=-3x2+6. 其中y隨x的增大而減小的函數(shù)有________（填序號）.

2. 求下列函數(shù)的最值.

（1）y=-3x+4（-1≤x≤3）______;

（3）y=-3x2+6______.

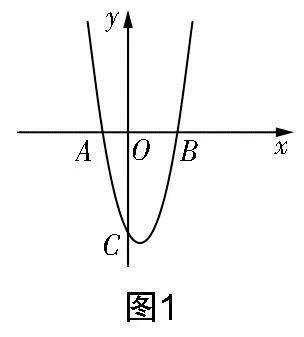
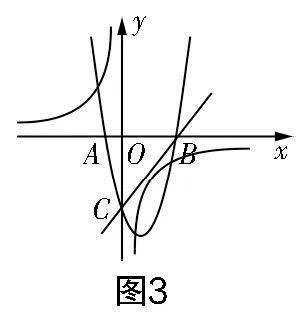
3. 已知函數(shù)y=ax2+bx+c（a≠0）的圖象如圖1所示，點A（-2，0），B（4，0）.

（1）結(jié)合圖象，你能說說這個函數(shù)有哪些性質(zhì)嗎？

②若D（0，y），E（3，y）是該函數(shù)圖象上的兩點，試比較y，y的大小;

③若D（2. 5，y），E（5，y）是該函數(shù)圖象上的兩點，試比較y，y的大小.

師生活動：課始學(xué)生獨立完成上述試題，教師巡視，給出答案，學(xué)生批閱、統(tǒng)計出錯率，教師不做講評.

設(shè)計意圖 題少而精，三道題涉及三種函數(shù)的性質(zhì)，即增減性、最值和對稱性，一道題對應(yīng)一個知識點的復(fù)習(xí)，能喚醒學(xué)生對相關(guān)知識的回憶，使得教學(xué)指向更加明確，教學(xué)更加高效.

（二）知識梳理

1. 思考自查題目的考點，梳理對應(yīng)的重要知識;分析自己的錯誤，記錄易錯點、解題策略[3].

2. 與組員交流對比，查漏補缺.

師生活動：學(xué)生獨立梳理、合作交流，教師適時補充，引導(dǎo)學(xué)生自我更正自查題中的錯誤.

設(shè)計意圖 有的放矢，有助于喚起學(xué)生對相關(guān)知識的復(fù)習(xí). 通過特殊到一般，挖掘習(xí)題背后隱藏的知識，此時學(xué)生對性質(zhì)的復(fù)習(xí)不一定全面，教師可指引學(xué)生從一次函數(shù)、二次函數(shù)、反比例函數(shù)的解析式、圖象與性質(zhì)方面進行對比復(fù)習(xí).

（三）典例精析

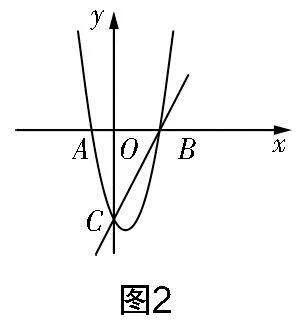
例1 如圖2所示，已知點B（4，0），拋物線y=x2+bx+c（a≠0）的圖象如圖所示，其對稱軸為直線x=1，求拋物線和直線BC的解析式.

問題1：你能求出拋物線和直線BC的解析式嗎？用什么方法？

追問：采用這種方法求函數(shù)解析式的一般步驟是什么？

師生活動：學(xué)生自行求出函數(shù)解析式，教師巡視，學(xué)生說出答案和解法，教師引導(dǎo)學(xué)生說出利用待定系數(shù)法求解析式的一般步驟.

設(shè)計意圖 求函數(shù)解析式的難度不大，學(xué)生易于完成. 利用函數(shù)圖象，我們?nèi)菀浊蟮煤瘮?shù)的解析式;反過來，如果知道了函數(shù)的解析式，我們也能夠畫出函數(shù)的圖象. 通過問題1，函數(shù)核心知識的學(xué)習(xí)得到了有效反饋.

例2 （1）求下列方程（組）的解：

（2）求下列各組不等式的解：

問題2：你能求出上述方程（組）、不等式的解（解集）嗎？

追問1：結(jié)合函數(shù)圖象，你能夠快速求出上述方程（組）、不等式的解（解集）嗎？

追問2：你能說一說函數(shù)、方程（組）、不等式之間的關(guān)系嗎？

師生活動：學(xué)生自行求出上述方程（組）、不等式的解（解集），教師巡視與指導(dǎo)，學(xué)生說出答案，教師引導(dǎo)學(xué)生利用圖象求解，總結(jié)三者之間的關(guān)系.

設(shè)計意圖 一般情況下，多數(shù)學(xué)生用代數(shù)法求解，教師引導(dǎo)學(xué)生用數(shù)形結(jié)合方法來求解，以降低學(xué)習(xí)難度. 第（2）題的②③問求二次不等式的解集，其在初中數(shù)學(xué)中未作定性要求. 對部分學(xué)生來說，求解有一定困難，此處意在引導(dǎo)學(xué)生用數(shù)形結(jié)合的觀點思考問題. 學(xué)生由此會找到函數(shù)、方程（組）、不等式之間的關(guān)系：①函數(shù)與x軸交點的橫坐標即為對應(yīng)的方程的解;②函數(shù)的圖象位于x軸上方（下方）時自變量的取值范圍即對應(yīng)不等式大于（小于）0的解集;③方程組的解即為兩函數(shù)的交點坐標;④ax2+bx+c>ax2+bx+c（或ax2+bx+c<ax2+bx+c）的解集即為函數(shù)y=ax2+bx+c的圖象位于函數(shù)y=ax2+bx+c的圖象上方（下方）時自變量的取值范圍.

（四）練析

1. 求不等式x3-3x2-6x+8>0的解集.

2. 豎直上拋的小球離地高度是它運動時間的二次函數(shù). 小軍相隔1 s依次豎直向上拋出兩個小球，假設(shè)兩個小球離手時離地高度相同，在各自拋出后1.1 s時到達相同的最大離地高度. 第一個小球拋出后t s時在空中與第二個小球的離地高度相同，則t的值為______.

師生活動：學(xué)生獨立思考，自行分析;小組合作，共同探究，得出結(jié)果;學(xué)生上臺展示思路與方法;教師點撥與評價.

（五）升華

1. 通過本節(jié)課的學(xué)習(xí)，你學(xué)到了哪些知識？

2. 在學(xué)習(xí)的過程中，滲透了哪些思想方法？

師生活動：學(xué)生獨立思考，再小組交流，全班共享討論結(jié)果，教師給予適時評價與補充.

設(shè)計意圖 反思解題方法，整合知識結(jié)構(gòu)，滲透數(shù)學(xué)思想，提升學(xué)生分析與解決問題的能力，形成知識模塊.

幾點感悟

（一）實施大單元復(fù)習(xí)課教學(xué)，要基于學(xué)生的學(xué)情

數(shù)學(xué)教學(xué)既要體現(xiàn)數(shù)學(xué)學(xué)科的特點，又要符合學(xué)生的實際;既要保證學(xué)生“吃得下”，又要保證學(xué)生“吃得飽”. 因此，教師必須根據(jù)學(xué)生的學(xué)習(xí)實際，適時地引導(dǎo)學(xué)生采取不同的學(xué)習(xí)方式. 設(shè)計大單元復(fù)習(xí)課教學(xué)，教師必須知道學(xué)生的學(xué)習(xí)認知點在哪里，學(xué)習(xí)困難點在哪里，學(xué)習(xí)的終點在哪里，然后在起點和終點之間，設(shè)置適合學(xué)生的學(xué)習(xí)路徑.

（二）實施大單元復(fù)習(xí)課教學(xué)，要踐行學(xué)為中心，發(fā)展學(xué)生的建構(gòu)能力

實施大單元復(fù)習(xí)課教學(xué)，教師要關(guān)注學(xué)生的基本活動經(jīng)驗，以學(xué)生為中心，通過創(chuàng)設(shè)聯(lián)系性、理解性、拓展性、歸納性的問題，督促學(xué)生有方向地梳理，有思路地歸納，促進學(xué)生思考，促使知識的發(fā)生、發(fā)展過程更合理，使學(xué)生在掌握基礎(chǔ)知識、感悟數(shù)學(xué)思想的過程中發(fā)展自己的建構(gòu)能力，提升自己解決問題的能力.

參考文獻：

[1]呂世虎，吳振英，楊婷，王尚志. 單元教學(xué)設(shè)計及其對促進數(shù)學(xué)教師專業(yè)發(fā)展的作用[J]. 數(shù)學(xué)教育學(xué)報， 2016，25（05）： 16-21.

[2]鄭學(xué)濤，朱向東. 基于課程標準的單元教學(xué)設(shè)計和實施建議——以魯教版《特殊四邊形》一章為例[J]. 中學(xué)數(shù)學(xué)雜志，2021（02）： 17-20.

[3]蘇文濤. 信息技術(shù)下基于CLES模型的問題解決復(fù)習(xí)課教學(xué)淺談[J]. 數(shù)學(xué)教學(xué)通訊，2021（35）：20-22.