強化分類思想 發展數學素養

[摘 要] 分類思想是重要的數學思想方法之一，其對培養學生的思維邏輯具有相當重要的作用. 在實際教學中，教師應重視加強分類討論思維模型訓練，指導學生合理應用分類思想解決問題，以此訓練學生思維的條理性和概括性，發展學生的數學素養.

[關鍵詞] 分類思想;分類意識;數學素養

無論在平時作業中，還是在大型考試中，因“分類不當”“忘記分類”等情況而失分的情況常有發生. 究其原因是學生缺乏分類意識，無法掌握分類對象的分類標準，加之學生平時做題后不重視反思歸納，使得學生在面對分類問題時常常出現錯誤. 在日常教學中，教師要加強學生分類意識的培養，適度增加應用分類思想解決問題，從而讓學生在問題的解決中逐漸積累經驗，升華認知，提升素養. 下面筆者就如何培養學生的分類意識，發展學生的分類思想，談談自己的看法.

在審題中發現分類信息

審題是解題的第一步，也是關鍵的一步. 通過審題理解題意，挖掘題設中的顯性條件和隱性條件，尋找解決問題的突破口.

例1 在Rt△ABC中，已知AC=3，BC=4，求AB的長.

問題給出后，很多學生不假思索地直接給出AB的長為5. 為了讓學生自己發現問題，教師引導學生說出思考過程.

師：說說你的解題過程. （教師點名讓學生回答）

生1：我先畫出Rt△ABC，其中∠C=90°，Rt△ABC的兩條直角邊長分別為3和4，根據勾股定理可以得出Rt△ABC的斜邊AB的長為5.

師：其他同學也和生1的想法一樣嗎？

有些學生點頭表示贊成生1的想法，有些學生提出異議，此時教師讓給出“AB邊的長為5”的學生重新仔細讀題. 學生再次讀題后找到了問題所在，順利地解決了問題.

教學分析：在解題過程中，受定式思維的影響，有些學生或添加“∠C=90°”這一條件，或認為3和4就是直角邊長，繼而得到的答案不完整. 然本題中并沒有指定∠C是直角，也沒有說明AC和BC是直角邊，所以在解決此類模糊性問題時，需要分類討論. 本題分兩種情況進行討論：一是已知兩條邊為直角邊;另一種是一條邊是直角邊，一條邊是斜邊. 在教學中，教師沒有直接給出評價，而是讓學生再次仔細讀題，讓學生自己發現問題所在，以此通過析錯、糾錯等過程培養學生思維的嚴謹性，推動學生全面發展.

在日常教學中，教師應重視讀題訓練，讓學生明確問題的關鍵信息. 在解決幾何問題時，應引導學生將文字語言和符號語言轉化為圖形語言，借助幾何圖形的直觀尋找解題的突破口. 在解題過程中，當學生的思維受阻時，應鼓勵學生重新讀題，以此突破障礙，形成正確的解題思路. 對于例1，之所以很多學生解題時出現了錯誤，就是因為學生沒有理解題意，想當然地認為給出的兩條邊是直角邊，繼而得出的答案不完整. 其實，例1中的模糊性語言就是關鍵信息，讀題時應及時捕捉，并在解題時合理分類，以此形成正確的解題思路.

例2 畫出函數y=x-1的圖象，說說該函數具有怎樣的性質. （至少說出2條）

教師預留2分鐘的時間讓學生讀題，然后與學生共同交流.

師：誰來說一說，你是怎么想的？

生2：要想畫出該函數的圖象，首先應該去掉絕對值符號.

師：你能詳細說一說該如何去掉絕對值符號嗎？

生2：要去掉絕對值符號，需要對（x-1）進行分類討論. 當x-1≥0，即x≥1時，函數為y=x-1;當x-1<0，即x<1時，函數為y=-x+1.

師：分析得很有道理，你是如何想到這樣分類的呢？

生2：我是結合之前學習絕對值時的經驗想到的. 在去掉絕對值符號時，需要看里面的數是正數、負數，還是0. 如果是正數或0，可以直接去掉絕對值符號;如果是負數，需要取它的相反數. 結合這一經驗，可以將函數y=x-1進行分類.

師：說得很好，已知條件中沒有給出自變量x的取值范圍，這樣我們也就無法確定（x-1）的正負，所以在面對x-1這一模糊條件時，需要進行分類討論.

在日常學習中，會遇到許多類似的出現模糊信息的問題，解題時一定要引導學生認真讀題，及時捕捉題設信息中的“弦外之音”，以此順利找到解題的突破口，高效地解決問題.

在問題中確定分類標準

確定分類標準是實施分類討論的關鍵. 數學對象的分類標準是千差萬別的，若思考的角度不同，出發點不同，分類標準會有所不同，分類結果和解題過程也會有所不同，因此分類標準的確定需要具體問題具體分析.

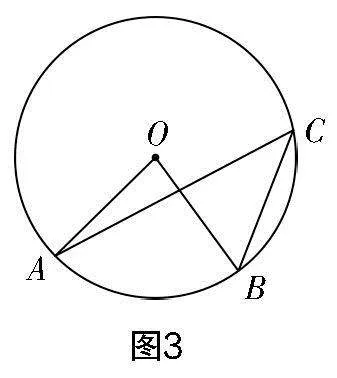
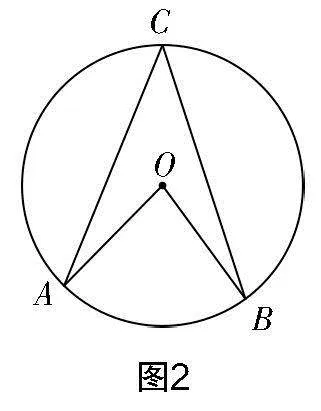
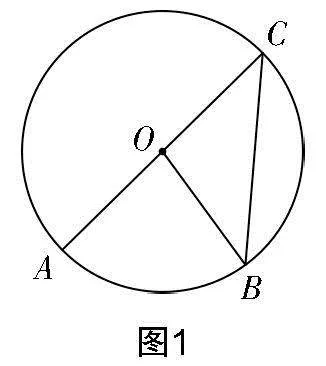
例3 在圓O中，A，B是圓上任意兩點，試探究弧AB所對的圓周角與圓心角之間的數量關系.

問題給出后，教師先讓學生動手畫圖，然后組內交流.

追問：大家通過動手操作發現，弧AB所對的圓周角有無數個，那么這些角存在怎樣的數量關系呢？它們與圓心角又存在怎樣的數量關系呢？

學生通過觀察和測量得到無數個圓周角的大小相等，且等于圓心角的一半的猜想. 但是猜想并不能作為結論，猜想的證明自然成了研究重點. 對于無數個角，顯然逐一證明是不現實的，為此在驗證時需要對其進行分類. 學生通過觀察、思考、交流，明確根據所對的圓周角與圓心O的相對位置進行分類（如圖1、圖2、圖3）：①圓心O在∠ACB邊上;②圓心O在∠ACB內;③圓心O在∠ACB外. 得到圖形后，可以根據三角形外角和、等邊對等角等相關性質證明結論，這里就不一一闡述了. 這樣通過分類討論不僅解決了“無數個”的問題，也得到了同弧所對的圓周角與圓心角之間的數量關系.

很多時候分類標準不是一眼就能看到的，需要在解決問題的過程中逐漸確定. 在日常教學中，教師要引導學生不斷地學習與積累，逐步提高自身分析和解決問題的能力，提高自身數學素養.

在反思中積累分類經驗

反思是加深知識理解，積累活動經驗，發展數學思維的重要途徑，其在數學學習中是必不可少的. 在日常教學中，教師要創設一定的機會引導學生反思，充分發揮反思的力量，提升學生的數學能力和數學素養. 分類能力的培養是一個慢過程，需要在日常教學中不斷引導學生去學習和感悟. 教師作為課堂教學的組織者，應為學生營造一個自我反思、自我歸納的良好的學習氛圍，讓學生在反思和歸納中逐步優化認知結構，提升分類能力.

為了讓學生在反思中積累分類經驗，提升數學學習能力. 針對以上3個案例，教師結合課堂生成創設如下問題：

（1）對于例1，你認為出錯的原因是什么？通過問題的解決，你積累了哪些讀題經驗？

（2）對于例2，將x-1分類的原因是什么？你收獲了哪些經驗？

（3）對于例3，為什么要對∠ACB進行分類？你是如何想到根據圓心O所在的相對位置來分類的呢？從中你積累了怎樣的經驗？結合已有經驗，你還能想到類似的實例嗎？

在日常教學中，當一些典型的問題求解后，教師應鼓勵學生回頭看，除了看解題思路外，還要歸納自己所想、所思、所惑，體會蘊含其中的數學思想方法，感悟問題的本質，以此逐步將知識內化為能力. 對于問題（3），教師可以啟發學生聯想“三角形內角和的證明”. 三角形有無數個，對于這種“無限”的問題，首先要將其轉化為“有限”，由此確認可以根據三角形的角進行分類，即分類為直角三角形、銳角三角形、鈍角三角形. 不過對于不同形狀的三角形，其證明方法是相同的，所以證明時不需要逐一證明.

這樣通過反復感知、反復錘煉，可以幫助學生深刻領悟分類討論的內涵，幫助學生積累豐富的分類經驗，從而為分類討論的合理應用保駕護航.

在內化遷移中提升分類素養

在數學教學中，不僅要提升分類能力，還要將其轉化為一種素養，這樣學生在解決分類問題時，才能敏銳地捕捉分類信息，科學制定分類標準，形成邏輯嚴謹、層次分明的解題策略. 在具體教學中，應指導學生應用分類討論方法解決問題，并讓學生在問題的解決中不斷探索、不斷反思，逐步將知識內化為能力，升華為素養.

例如，針對例3中所研究的內容，教師不妨設計如下問題：在圓O中，AB是圓O的弦，C，D是圓O上的任意兩點. 已知∠ABC=30°，∠ABD=45°，求∠COD的度數.

題設中沒有明確C，D相對于AB弦的位置，若能捕捉到這一模糊信息，問題即可迎刃而解. 這樣借助情境，引導學生捕捉關鍵信息，既能提升學生的探究欲，又能加深學生對知識的理解，讓學生的分類素養在問題的解決中得以升華.

總之，學生分類素養不是一朝一夕養成的，需要在日常教學中不斷發展與完善. 在日常教學中，教師要創造機會讓學生自己去提煉、去感悟、去積累，逐步鍛煉學生的數學思維，提升學生的數學素養.