數(shù)學微型探究活動存在的問題與應對措施的研究

[摘 要] 微型探究活動的開展，可進一步深化學生對知識重點、難點的理解，培養(yǎng)學生的數(shù)學意識. 實踐中，數(shù)學微型探究存在如下幾類問題：學情掌握不準、要素配置錯位、難易程度失控、活動設計失當、探究方法失調(diào). 為此，研究者借助幾個教學實例分別針對每一種情況，談一些應對措施與思考.

[關鍵詞] 微型探究;活動;學情

數(shù)學微型探究活動是指根據(jù)學情與教學內(nèi)容的特點，擇取一個合適的角度，圍繞教學重點與難點開展短時間的探究活動，能為學生創(chuàng)造探究機會，形成活動體驗. 這種探究活動屬于定向探究類型，需結合學生的實際需求與教師的教學經(jīng)驗設計教學活動，活動以用時短、切口小、符合實際、靈活等為特點. 這種探究活動的開展，可進一步深化學生對知識重點、難點的理解，培養(yǎng)學生的數(shù)學意識. 方法雖好，但實際實踐中仍存在一些問題，本文將每一種問題羅列出來，并借助實例談一些應對措施與思考.

學情掌握不準

學情診斷是設計教學方案的首要步驟，教師若無法精準掌握學情，那么設計的教學方案則有可能偏離學生的認知區(qū)域，導致教學的失敗. 傳統(tǒng)的學情診斷以發(fā)放學案或訪談為主，這種方法搜集學情費時費力，而且還會出現(xiàn)判斷失誤的現(xiàn)象. 甚至有些老師在設計教學活動之前，完全憑借自身的經(jīng)驗來判斷學情，這種脫離課程標準與教材要求的做法，會讓教師對學情產(chǎn)生失察現(xiàn)象，致使不少學生難以全身心地參與到微型探究活動中來.

事實證明，新課標引領下的數(shù)學學情診斷，可借助信息技術手段，如極課大數(shù)據(jù)的應用，從學生的作業(yè)、練習訓練中提取數(shù)據(jù)，精準判斷學情，為教學做準備.

案例1 “二次函數(shù)與一元二次方程”的教學.

例題教學完畢后，為了進一步鞏固學生對教學重點與難點的理解，教師設計了如下問題：若二次函數(shù)y=x2+2ax+b2與y=x2+2bx+c2的圖象和坐標橫軸存在兩個不重合的交點，函數(shù)y=x2+2cx+a2的圖象和坐標橫軸相交嗎？說明理由.

本節(jié)課教學重點與難點在于探索二次函數(shù)圖象和一元二次方程根之間存在怎樣的關系. 因為學生所接觸的二次函數(shù)以數(shù)字系數(shù)的二次函數(shù)為主，本例顯然超出了常規(guī)范圍，三個帶字母系數(shù)的二次函數(shù)讓大部分學生感到束手無策，同時此問也超出了課標要求，缺乏探索意義.

案例2 “直線與圓的位置關系”的教學.

問題 如圖1，已知矩形ABCD中，AB=20 cm，BC=4 cm，若點M以4 cm/s的速度由點A開始，沿著A，B，C，D進行有序運動，點N則以1 cm/s的速度由點C處開始，沿著CD邊進行運動，若點M，N分別從點A，C同時出發(fā)，在點M，N中的一個點抵達點D時，另一個點立即靜止不動. 若圓M，N的半徑均為2 cm，求點M在運動多久時，圓M、N間僅有一個交點？

分析 此例是結合教學內(nèi)容特點與學生實際情況而編制的一道微型探究活動題. 題的背景為兩個動態(tài)變化的圓，這就給學生的理解帶來了較大的障礙，關于兩個圓僅有一個切點的問題，大部分學生可以理解，但關于兩個圓的變化過程，卻讓不少學生感到棘手. 本題兩個圓在運動過程中存在三次只有一個交點（外切）的情況，想要從真正意義上探索這兩個圓的關系，著重在于探索兩個圓心在運動時存在什么樣的關系. 顯然，這超出了學生的認知范疇，導致學生難以理解. 因此，本題也是在沒有精準把握學情的基礎上所設計的，探究活動缺乏可行性.

類比兩個案例，不難發(fā)現(xiàn)微型探究活動的設計離不開對學情的精準診斷. 若教師完全不顧及課標要求、教學內(nèi)容的特點以及學生的實際認知水平，僅憑自己的經(jīng)驗設計微型探究活動，則會讓探究內(nèi)容變得過深、過寬，拉大學生與問題之間的差距，探究活動也因此難以達成預期的目的，更有甚者還產(chǎn)生負面影響.

想要從根本上規(guī)避這個問題，最好的方法就是擇取適切的探究活動內(nèi)容. 如案例1的探索，可通過對數(shù)字系數(shù)的減少來設計活動;案例2則可將探究問題更換成“兩圓在直線上運動”. 同時，教師作為課堂的引導者，需時刻關注學生在探索過程中的情況，必要時可為學生的思維搭建“腳手架”，讓學生有明確的思考方向. 若學生表現(xiàn)出探索困難，教師還可借助課堂交流的模式啟發(fā)學生的思維，讓學生在師生、生生積極的互動中提升探索效率.

要素配置錯位

數(shù)學微型探究活動的設計涵蓋了問題背景、知識內(nèi)容、活動程序、思維空間等諸多要素，這些要素均在教學目標的統(tǒng)領下互相調(diào)適、配合. 然而，實踐發(fā)現(xiàn)，有些教師設計微型探究活動會忽略這些要素的關聯(lián)性，常因配置錯位而導致探究活動偏離教學目標的情況發(fā)生，這種虛化教學目標，弱化教學成效的設計方案，值得每一個教師去關注與思考.

案例3 “用二元一次方程組解決問題”的教學.

教師為了幫助學生更好地理解用二元一次方程組解決實際問題，有針對性地設計了如下微型實驗探究活動.

活動1 分別取10枚一元硬幣與10枚五角硬幣，按照幣值分成兩摞重疊擺放，用刻度尺分別測得兩摞硬幣的厚度;而后用天平分別稱出這兩摞硬幣的質量，同時計算每一枚一元與五角硬幣的質量是多少.

活動2 將一些一元與五角的硬幣混合并疊放在一起，用刻度尺測量出厚度，并稱出所有硬幣的質量，借助二元一次方程組獲得兩種硬幣的個數(shù)，算出總金額.

活動3 以小組為單位，提一些與硬幣活動相類似的問題，并借助二元一次方程組來解決所提出的問題.

二元一次方程組是初一年級所接觸的內(nèi)容，而用天平稱重卻要到初二年級才有所涉及. 以上活動需要應用到天平稱重這一操作，因此教師需先教會學生如何正確使用天平，顯然這個過程偏離了本節(jié)課教學的主題. 此活動，教師若直接將硬幣的厚度與質量呈現(xiàn)給學生，未嘗不可.

微型探究活動的開展需緊扣教學目標來設計，要杜絕為了加強數(shù)學實驗機會，而不管教學需求就盲目地添加操作活動，致使解決問題的過程嚴重偏離教學主題，浪費寶貴的課堂時間. 想要避免此類要素配置錯位的問題，教師在設計教學活動時就要以教學目標作為出發(fā)點，提前預測課堂中可能會出現(xiàn)的問題，將各種不匹配的因素逐一轉化、化解.

如本例，教師需明確認識到天平稱物為本節(jié)課的輔助活動，教師可直接給出具體數(shù)據(jù)，或自主動手操作，也可以指派一個動手能力較強的學生進行操作.

難易程度失控

微型探究活動離不開問題的引導，而問題的難易程度又決定了探究的質量. 有些教師在設計問題時，沒有考慮到學生的實際認知水平，試圖通過一定難度的問題拔高學生的思維，殊不知，難度過大的問題會嚴重消減學生的探究信心，阻礙學生的探究步伐;還有些教師為了讓所有學生都能積極地參與到探究活動中，設置過于簡單的問題，導致學生體會不到探究帶來的挑戰(zhàn)性與成就感. 因此，過難或過于簡單的問題都不利于學生思維的成長.

案例4 “勾股定理的逆定理”的教學.

問題1 勾股數(shù)有很多組，你們能列舉100組嗎？

學生雖然能說出一部分，但受課堂時間與學生認知的局限，無法在短時間內(nèi)列舉100組勾股數(shù). 為此，教師為學生的思維搭建了如下平臺.

問題2 若m，n為正整數(shù)，（m2+n2）2-（m2-n2）2=（2mn）2，讓c=m2+n2，a=m2-n2，b=2mn，據(jù)此可寫出幾組勾股數(shù)？

觀察本例，第一個問題要求學生說出的勾股pfqIbsh+ssxEJiit52PJE0s+9uSeccKBi7M4XIJtdSQ=數(shù)組的量過大，顯然超出了課堂基本思維容量，學生也難以從中探尋出一般規(guī)律;第二個問題雖然降低了難度系數(shù)，但教師直接將公式（m2+n2）2-（m2-n2）2=（2mn）2提供給學生，導致問題沒有難度可言，那就喪失探究的意義. 其實，第二問中的公式對學生而言是一個具有探究價值的內(nèi)容.

另外，通過本題教師還可以帶領學生從a2+b2=c2著手，借助a2=（b+c）（b-c），讓b-c=1，僅需b+c為一個完全平方數(shù)，則可構造出無數(shù)組勾股數(shù). 想要把握好探究問題的難易程度，離不開對學生實際認知水平的判斷與探究課題的遴選，適切的探究活動才能達到預期的目標.

活動設計失當

微型探究活動同樣需要經(jīng)歷實驗操作、觀察等步驟，那么在設計活動方案時，則需要思考如下幾個問題：與微型探究相關的活動有哪些;各項活動需滿足什么要求;怎樣調(diào)控活動過程;如何應用活動結論等. 若考慮不周，很有可能會影響探究成效.

案例5 “平面圖形的認識”的教學

授完第一節(jié)課后，教師要求學生自制測風儀，具體要求為：將一張畫有量角器的紙張剪貼在硬紙板上，并在量角器的中心打孔、穿線，線的另一端系上乒乓球. 第二節(jié)課上，教師要求學生利用自制的測風儀對著電風扇吹，同時記錄細線偏離鉛垂線的角度數(shù)據(jù)，對照教師所提供的“風速對照表”來測量風速.

學生自主操作，結果因自制的測風儀沒有充分考慮到材料規(guī)格、工藝等要求，導致操作時角度和風速與對照表出現(xiàn)了不匹配的情況，其主要原因是自制的測風儀過于簡陋，無法應用風速對照表. 其實，這是一個很有意義的探究活動，但因為教師在工具設計指導上沒有考慮周全，導致探究活動無法發(fā)揮其應有的價值.

回顧這個探究活動，學生費時費力地自制測風儀，對課堂本充滿期待，但在實際應用時卻宣告失敗，這嚴重挫傷了學生的積極性. 活動應從求簡的角度進行改進，如教師為學生提供制作材料，鼓勵學生以小組合作的方式制作測風儀，將測風速更換為在同一風速下，不同角度風速大小的探索，引導學生建立角度與風速呈大致對應的模型，可成功激發(fā)學生的探索欲，顯著提高探究實效.

探究方法失調(diào)

開展微型探究活動的主要目的在于引導學生經(jīng)歷知識的發(fā)生、發(fā)展過程，感悟并理解知識的應用，獲得分析問題與解決問題的能力. 然而，實踐中有些教師只關注探究活動本身的設計，忽略數(shù)學思想方法的鋪墊，這種探究方法的失調(diào)難以從真正意義上發(fā)揮微型探究活動應有的價值.

案例6 “平行四邊形”的教學

當學生對平行四邊形的定義、性質等有所了解后，則進入思維拓展環(huán)節(jié)，為了進一步激活思維，一位教師設計了如下問題：

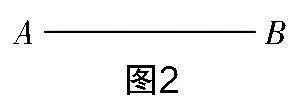
請用圓規(guī)在圖2上畫一個點P，讓點P位于AB的延長線上，并滿足PB=AB.

這是一個應用指定工具畫圖的問題，從學生已有的認知出發(fā)，僅有圓規(guī)難以獲得滿足題設條件的線段，因此很多學生看到這個問題都束手無策.

此探究活動的失敗，主要原因在于缺少了探究方法的鋪墊. 該探究活動首先需考慮的問題是圓規(guī)能構造出哪些圖形.

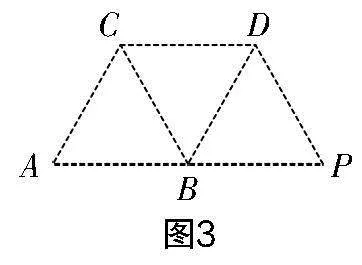
此問中，用圓規(guī)可以分別作出點C、D，讓△ABC與△DCB全等. 如圖3，四邊形ABDC為平行四邊形，同理構造平行四邊形PDCB.

綜上分析，本例可增加兩個問題作為學生思維“腳手架”：①用圓規(guī)在圖2中作點C，讓△ABC為等腰三角形;②繼續(xù)用圓規(guī)作點D，讓四邊形ABDC為平行四邊形. 在這兩個問題的點撥下，學生則能順利解決問題.

實踐證明，微型探究活動的方法中常蘊含了豐富的數(shù)學知識與思想，教師在設計探究活動時應考慮到這條暗線，對探究活動涉及的通性通法、數(shù)學思想、特殊方法等，做到心中有數(shù)，必要時借助一些小問題為學生的思維搭建臺階，讓學生在知識與方法的類比遷移中探尋數(shù)學本質.

總之，微型探究活動的開展既離不開對學情的精準診斷，又離不開教師的精心籌劃與判斷. 這也對教師的業(yè)務水平提出了更高要求，教師應將發(fā)展學力作為探究活動設計的載體，讓微型探究活動發(fā)揮其應用的價值.