經歷知識發生發展過

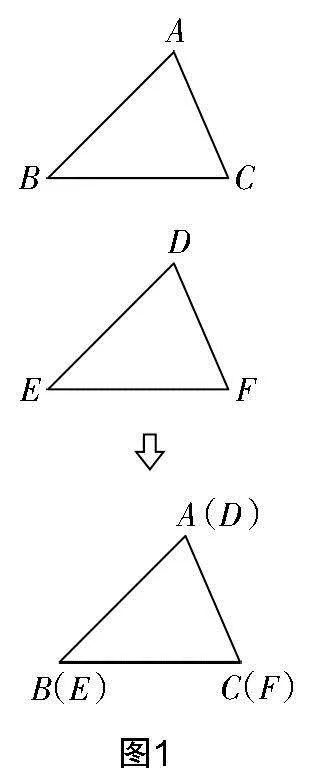
[摘 要] 數學教學需要教師遵循“以學生發展為本”的原則，引導學生經歷知識發生發展的過程，揭示數學本質. 文章以“探索三角形全等的條件（1）”為例，提出“追蹤數學的思維歷程，使學生親歷知識‘再發現’過程”“展示學生的思維歷程，使學生的思維空間得到拓展”的觀點.

[關鍵詞] 知識發生發展;數學本質;數學思維;三角形全等

經歷知識發生發展過程，就是經歷知識的發現、形成、深化、拓展和應用的過程. 數學知識發生發展過程包含數學家或數學教育家的思維過程. 在課堂教學中，教師應遵循“以學生發展為本”的原則，深入研究教材、教學內容和具體學情，引導學生循著數學家思維活動的軌跡深度探究，使學生自然更新與發展數學認知結構，自然提升數學思維能力. 下面，筆者以“探索三角形全等的條件（1）”為例，具體闡述如何巧妙設計教學過程，讓學生經歷知識發生發展過程，揭示數學本質，提升數學素養.

簡析教學過程

教學環節1：在舊知回顧中巧妙導入

問題1：你們還記得全等三角形的性質嗎？誰能通過符號語言進行描述？（如圖1所示，因為△ABC≌△DEF，所以AB=DE，BC=EF，AC=DF，∠A=∠D，∠B=∠E，∠C=∠F. ）

問題2：如何判斷兩個三角形全等呢？試著用符號語言描述. （學生進行相關描述，并生成：因為AB=DE，BC=EF，AC=DF，∠A=∠D，∠B=∠E，∠C=∠F，所以△ABC≌△DEF.）

問題3：從定義出發判定兩個三角形全等需要6個條件，那是否存在更加簡潔的方法呢？（教師順勢拋出課題）

評析 溫故而知新，復習舊知可以促進學生進行更加深入的思考. 課始，教師巧妙拋出問題，激活學生思維，引發學生對判定三角形全等進行思考，并順勢設置懸念，使學生產生一探究竟的欲望，為后續的深度探究做足準備.

教學環節2：在實踐操作中漸深探究

探究活動1：動手畫一畫.

活動素材：鉛筆、直尺、圓規、量角器、三角板、草稿紙等.

活動要求：先在草稿紙上畫一個大小適中的三角形，再利用上述準備好的素材，開動腦筋試著畫出一個三角形，使其與之前的三角形全等.

探究活動2：想一想，說一說.

（1）想一想你是如何作圖的，同桌兩人一組互相說一說.

（2）請學生代表闡述方法和結論.

學生活動：①直尺度量法（具體略）. 由此可見，僅僅保證兩條邊對應相等，兩個三角形不一定全等，唯有三條邊都相等，兩個三角形才全等. ②量角器測量法（具體略）. 由此可見，僅僅保證一個角相等，兩個三角形不一定全等;保證一個角與一條邊相等，兩個三角形也不一定全等;唯有兩個角與一條邊相等，兩個三角形才全等. ③尺規作圖法（具體略）. 由此可見，兩邊及一個夾角相等的兩個三角形全等.

探究活動3：其余同學有何疑問？提出來大家一起分析并解答.

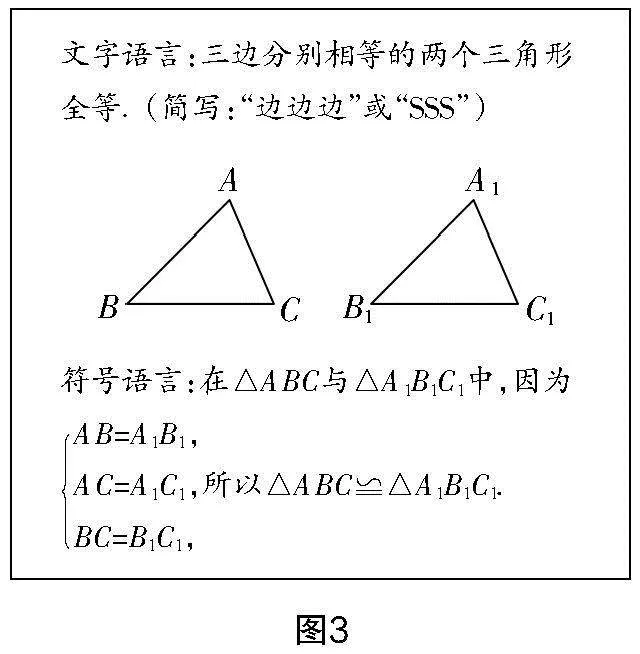
師生活動：學生很快大膽提出問題“一個或兩個條件是無法證明兩個三角形全等的，最少需要三個條件. 那一個或兩個條件無法證明，真的是這樣嗎？”教師鼓勵學生通過反例的方式來說明這個觀點是否正確. 學生很快提出如下觀點：①一個角或一條邊，“一副三角板中的兩個三角形滿足一個角對應相等，但它們不全等”“一副三角板中的兩個三角形滿足一條邊對應相等，但它們不全等”;②兩個角、兩條邊、一邊一角，“一副三角板中的60°角的對邊與45°角三角板的斜邊相等，且90°角對應相等，滿足一角、一邊相等，但它們不全等”“兩個不同大小的三角形對應角相等，但它們不全等”“從圖2所示的尺規作圖可以看出，△ABC與△ABC滿足兩條邊相等，但它們不全等”;③三個角、三條邊、兩邊一角、兩角一邊，“三個角的情況前面已經探索了，并得到不全等的結論”“在剛才的實踐活動中，組內多人畫了三條邊都相等的三角形，并剪下進行比較，發現所有三角形都重合，因此是全等的”.

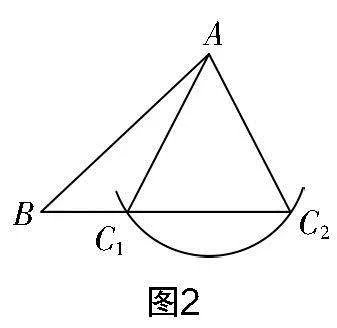
總結：上述活動中，大家給出的分析和總結都具有說服力. 尤其是針對三條邊都相等的情況，這也是本節課的研究核心——探索三角形全等的條件（1），見圖3. 后續我們還會針對性地探究剩余的兩邊一角與兩角一邊的情形……

評析 在這一環節，教師通過設計“做數學”的探究活動，帶領學生探索知識本質，并在探究中不斷疊加問題，引出知識線索，讓學生一個問題一個線索地探究下去，最終水到渠成地建構新知. 更重要的是，教師充分暴露了學生的思維歷程，讓學生在思考、表達、爭辯、討論等過程中有效提升了語言表達能力和數學歸納能力.

教學環節3：在回顧反思中深化認識

問題1：一起來梳理本節課所學，談談你的認識.

問題2：事實上，三角形全等在現實生活中應用廣泛. 上述現象說明了什么？（教師課件呈現日常生活中三角形穩定性的一些圖片，并列舉電動門，學生在觀察后一致認為“三角形具有穩定性”.）

評析 學生在新知得以建構后及時回顧和反思所學，可以完善認知結構，提升數學思維的敏捷性.

教學思考

1. 追蹤數學的思維歷程，使學生親歷知識“再發現”過程

數學知識都是由數學家研究得到的，但受篇幅和結構體系的制約，教材中的概念、規律和法則省略了數學家探索和發現的歷程. 這就需要教師在教學的過程中引導學生循著數學家探究的思維軌跡，體驗數學知識的“再發現”過程，從而在自主建構新知的同時培養探究精神和創新能力. 本課中，學生的探索過程實質上就是不斷類比、猜想、歸納、驗證的過程，從本質上來說就是新知發現的過程. 整個探究過程，學生的積極性較高，并深刻理解了知識本質，無痕培養了分類、探究、合作和歸納能力.

2. 展示學生的思維歷程，使學生的思維空間得到拓展

課堂教學的主體是學生，也就是說，思維活動的主體也是學生. 在課堂中，教師需要營造民主、寬松的課堂氛圍，讓學生自主參與到數學探究中，并充分展示自身的思維歷程，暴露困惑的同時展示擺脫思維困境的艱辛，從而在經歷坎坷的過程中體驗成功的快感，有效拓展思維空間. 本課中，教師遵循學生本位，充分演繹了教師的“引”與學生的“探”和諧統一，使學生在經歷確定三角形全等的條件的過程中思維自由馳騁，從而建構知識體系，培養思維的深刻性.

總之，教師應體現“以學生發展為本”的原則，讓學生經歷知識發生和發展的全過程，并結合“讓學”的理念驅動學生思考、探究與交流，充分展示學生的思維歷程，拓展學生的數學思維空間，提升學生的數學核心素養.