基于大單元教學的高中數學情境創設教學應用研究

【摘要】本文探討基于大單元教學的高中數學情境創設在教學中的應用，通過對大單元教學的分析，明確情境創設的類型和形式，并結合具體案例闡述情境創設在單元設計中的實施過程.研究表明，科學合理的情境創設能夠引導學生主動探究，深入理解數學知識，提升數學素養.

【關鍵詞】大單元教學;情境創設;數學建模;深度學習

1 大單元教學分析

依標據本，了解學情，熟悉大單元內容、目標、重難點及教學學業評價是重中之重.根據設計理念，設計結構化活動，分課時規劃以及實施與反思改進.

1.1 單元知識結構學習目標及內容解析

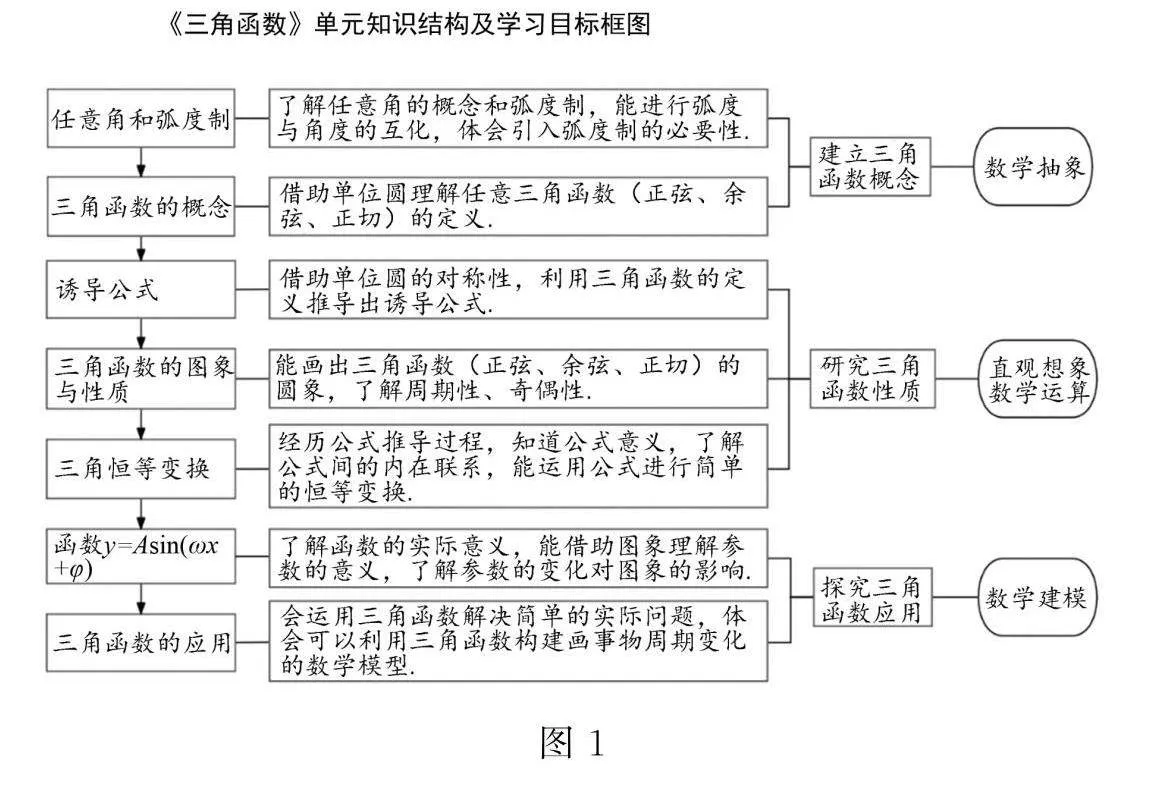
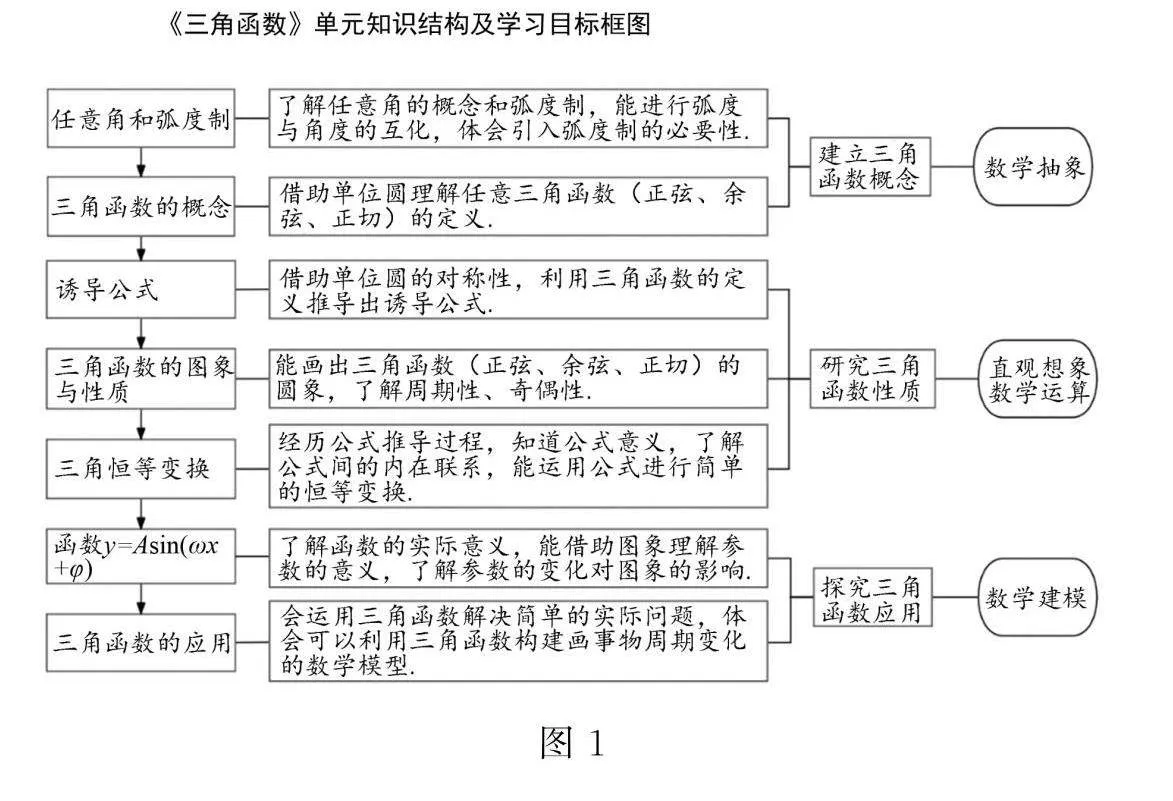
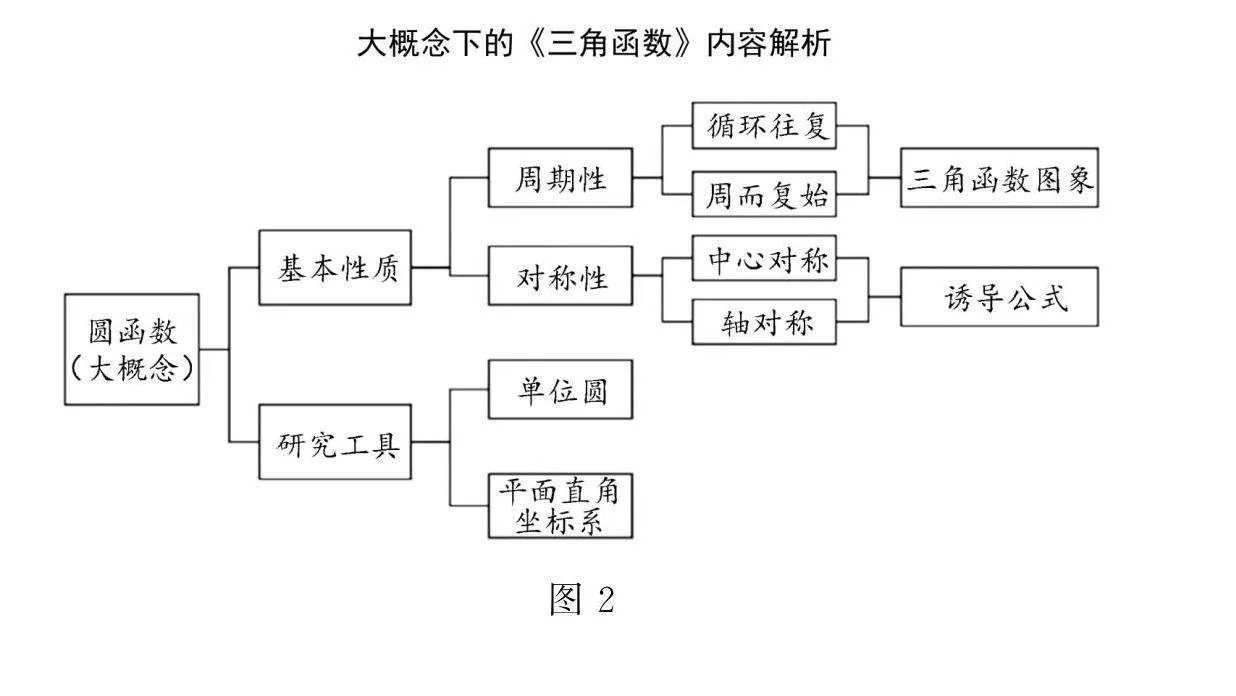
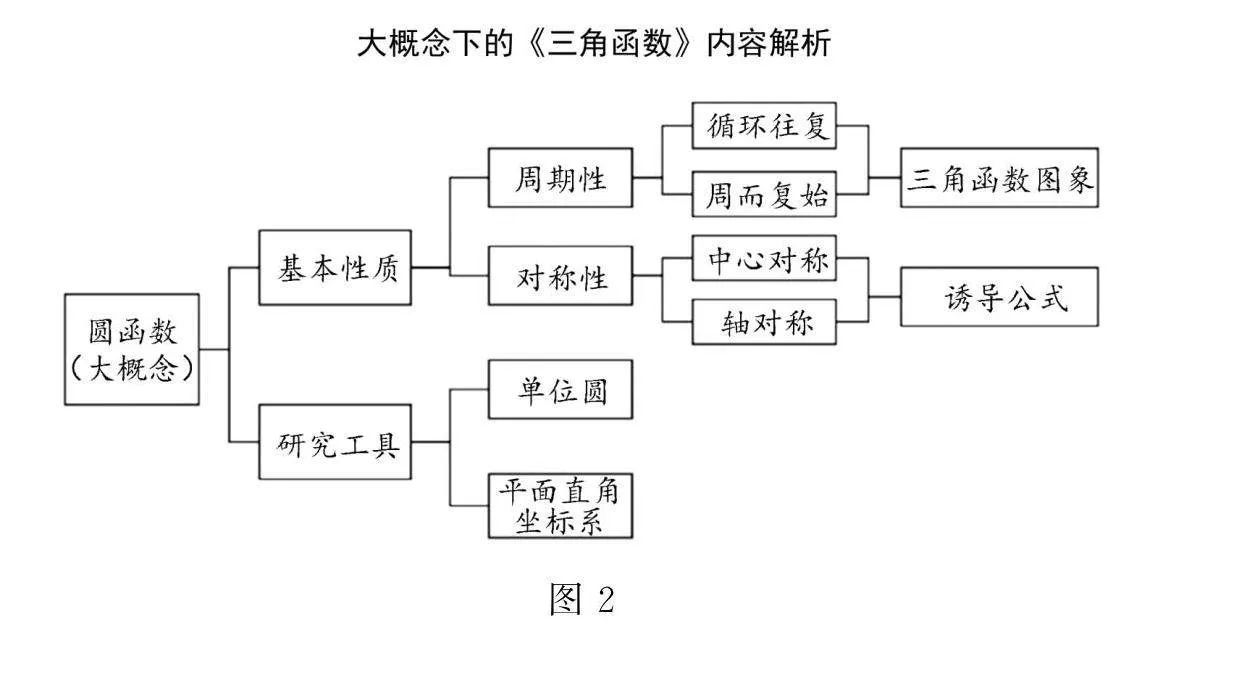
在進行“三角函數”單元教學時，需明確考查重點和難點，把握高考應試內容，避免陷阱.單一學習目標無法形成知識聯系，大單元教學可使學生知識完備化、系統化、網絡化.圖1、圖2為筆者設計的“三角函數”單元知識結構及學習目標、內容解析圖示.

1.2 學情診斷

學生已掌握函數概念與性質，對基本初等函數有一定研究經驗，但面對三角函數時，因其基于幾何元素的對應關系與已有經驗有偏差，導致理解定義和對應關系有難度.同時，學生的數學抽象、表達能力和獨立思考、反思質疑習慣仍需加強.

1.3 單元整體的設計構想

在教學過程中，我們需要高度關注三角函數的整體性和內在邏輯，通過思維導圖系統整理知識點，培養主動復習習慣，并結合提問、互動和集體活動，深化理解，培養整體學習意識，旨在提升學生的數學建模、直觀想象能力，增強數學應用能力和應試技巧，實現教學效果最大化.

2 情境創設在單元教學中的實施

2.1 情境創設的類型和情境形式

數學教學情境設計需遵循“真實性、數學性、科學性”原則，并考慮學生認知水平.常見情境包括經驗、生活、趣味、知識、社會和跨學科類，旨在激發學生學習動機和提升學習效果.以問題情境為核心，能激發學生認知沖突和主動思考.科學的情境能引導學生深入理解數學知識，體驗其價值，培養數學思維和素養.

2.2 數學情境創設在單元設計中的實施過程

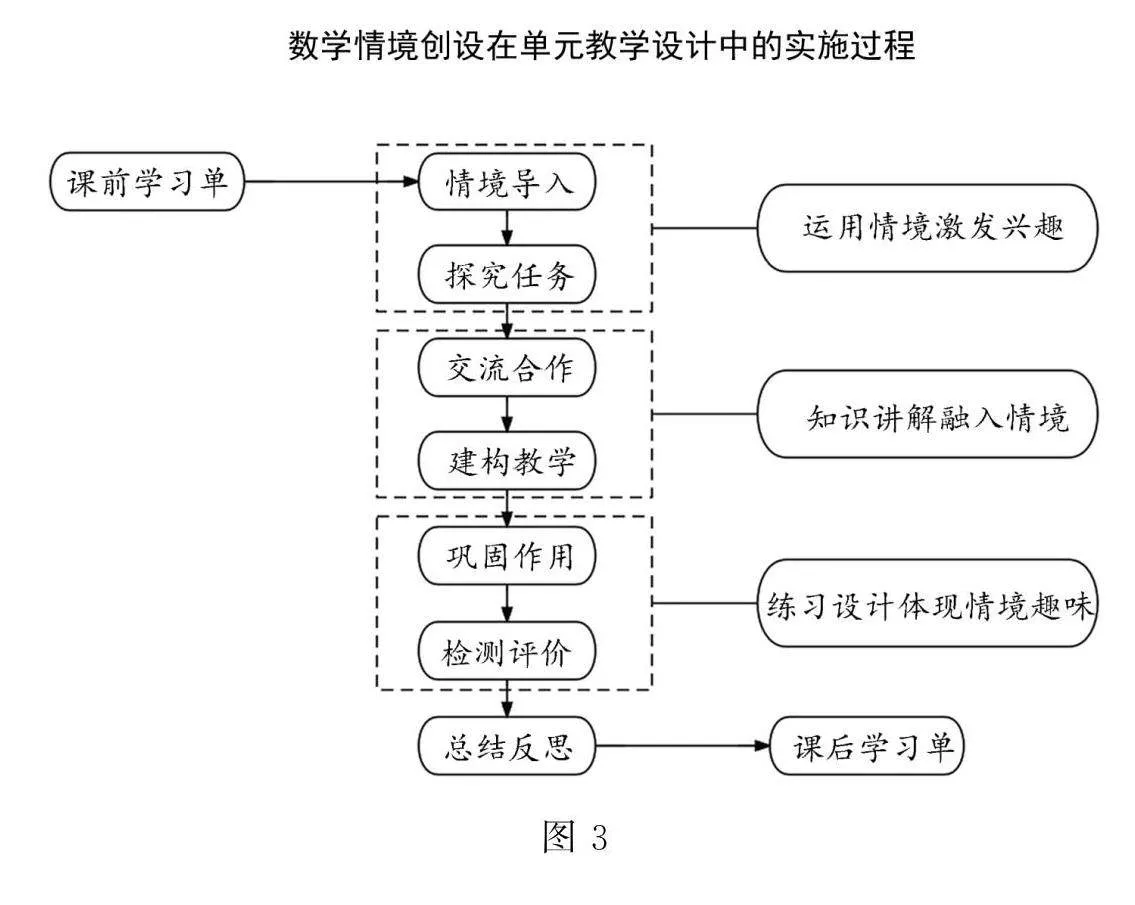
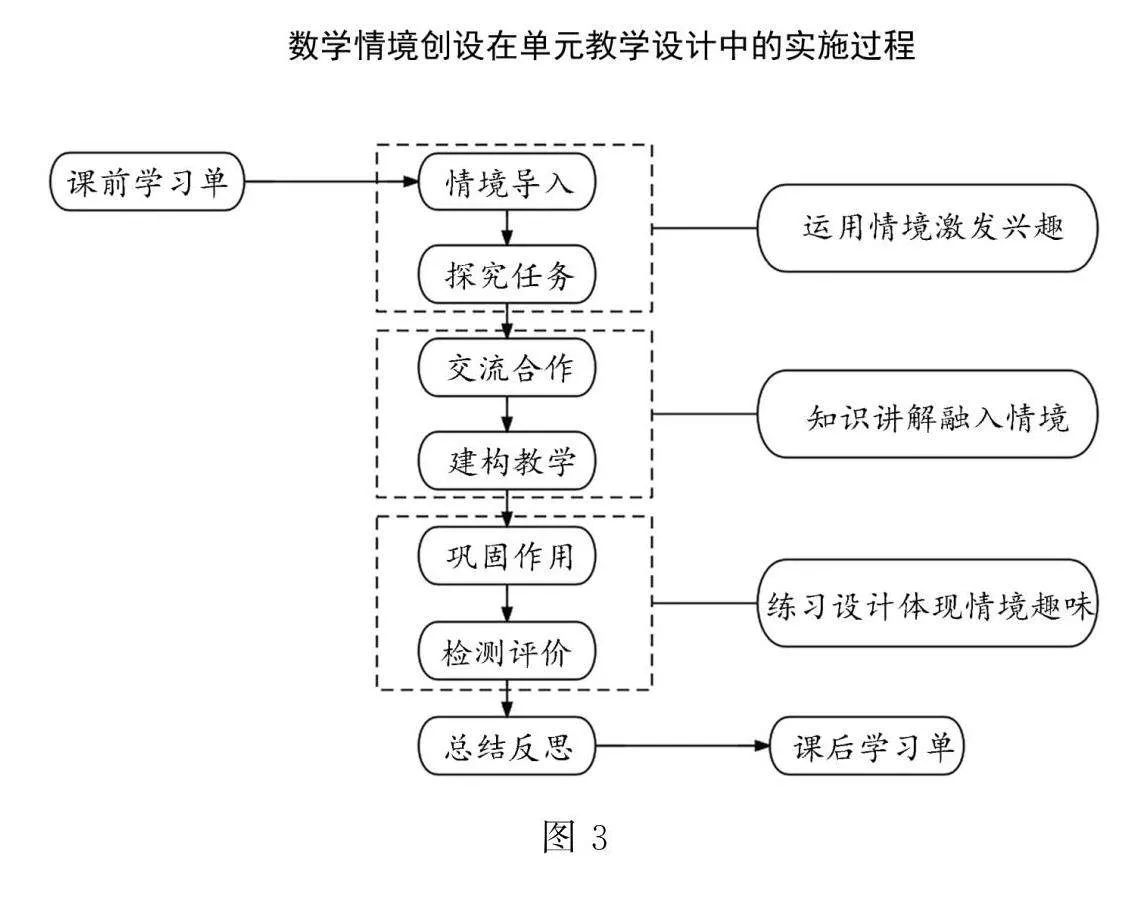
圖3是筆者設計的數學情境創設在單元設計中的實施過程.

2.3 情境創設案例

創設情境引導學生主動探究，發展學生能力和體驗數學過程.觀察分析情境資料，鼓勵學生猜測和探索數學問題.多角度引導提問，培養問題意識和探究欲望.新授課重探索，練習和復習課重常規.

案例1 在“5.2.1 三角函數的概念”中，通過生活情境和核心問題引導學生探索.

情境 倫敦的觀景摩天輪，游客乘坐在座艙P從A點出發，逆時針勻速旋轉.

核心問題 如何建立數學模型刻畫座艙P的位置變化？

問題 （1）單位圓O上點P以A為起點逆時針旋轉，如何刻畫其位置變化？

（2）是否有其他變量可以刻畫？

（3）這些變量間有何關系？

（4）當確定旋轉角∠ AOP時，能確定哪些量？

師生活動 圍繞核心問題展開互動，推進問題串的遞進延伸.

設計意圖 摩天輪作為情境引入，貼近生活，能夠吸引學生注意力.學生在有趣的問題中更易形成主人翁意識，享受學習，轉化學習動機，促進主動探索.

通過探究“如何建立數學模型刻畫座艙P的位置變化”，此“拋錨式”教學鼓勵學生深入探究和解決問題，而非依賴現成知識.學生圍繞核心問題，思考單位圓在建構三角函數概念中的作用.

設計小問題串引導學生逐步觀察：問題（1）關注單位圓上點位置的變化與旋轉角、弧長、點坐標的關系；問題（2）梳理變量間的關系，突出旋轉角和點坐標；問題（3）和問題（4）明確函數為刻畫變量對應關系的模型，建立相關函數模型解決問題.此問題串可以幫助學生形成結論，完整構建三角函數概念.

案例2 在“5.6.1 函數y=Asin（ωx+φ）”的學習中，利用學生已學的單位圓上點的運動規律，推廣至勻速圓周運動數學模型.通過筒車輪灌溉原理的實際情境，激發學生求知欲.

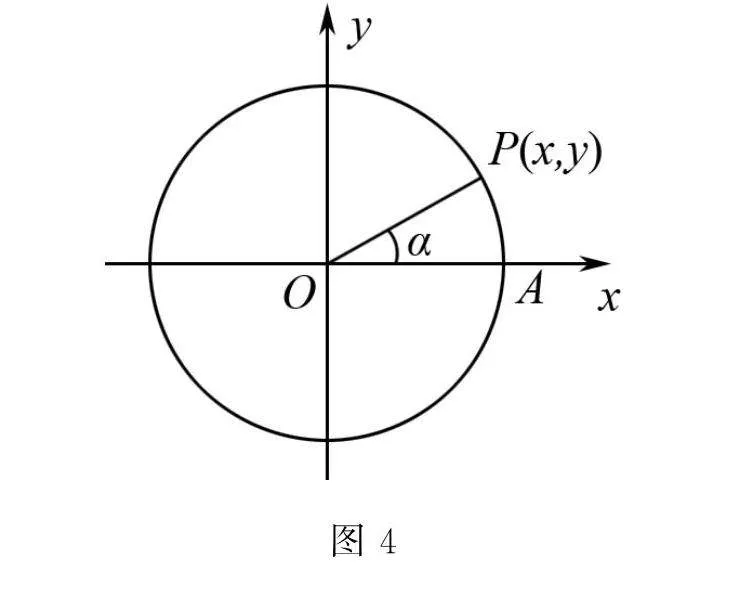
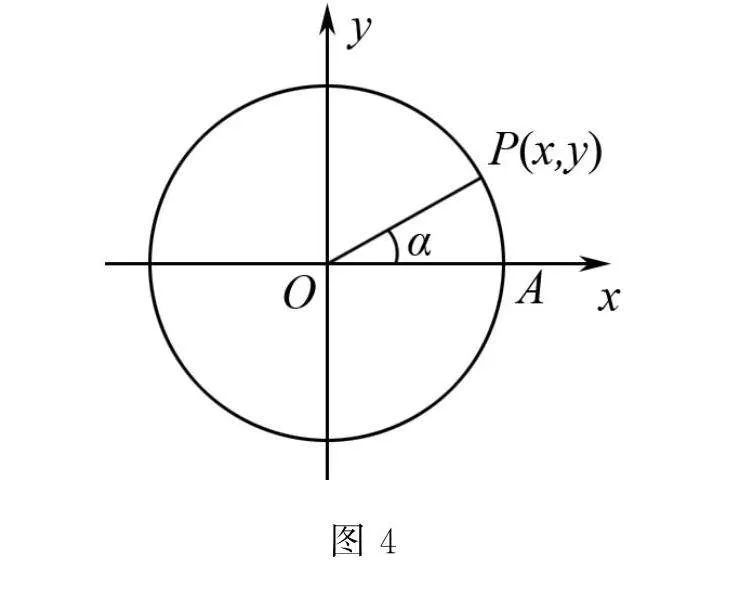
情境1 如圖4，單位圓O上的動點P以A（1，0）為起點沿逆時針方向旋轉角α到達點P，那么點P的坐標x，y可以由三角函數x=cosα，y=sinα來確定，求點P的坐標與運動時間t之間的關系.以A為起點，以單位角速度ω=1沿逆時針方向運動，經過時間t到達點P，角α與t之間有什么關系？點P的縱坐標y是時間t的函數嗎？

師生活動 學生回顧舊知并回答問題，教師引導討論現實生活中的圓周運動問題.單位圓上點的運動規律數學模型可推廣至勻速圓周運動.

設計意圖 從已知出發，掌握一般的勻速圓周運動數學模型是研究一般勻速圓周運動的基礎，從已知推廣到未知，拋磚引玉，創設實際情境進行函數y=Asin（ωx+φ）的研究學習.

情境2 筒車（圖5）是中國古代發明的一種灌溉工具.明朝科學家徐光啟在《農政全書》中詳細描述了其工作原理——利用筒車輪的圓周運動進行灌溉.假設水流量穩定，筒車上的盛水筒做勻速圓周運動，我們可將其抽象為質點在圓上的運動，進一步探討盛水筒距離水面的相對高度與時間的關系是否能用函數模型刻畫.

師生活動 讓學生分組討論，教師引導思考.因為筒車運動具有周期性，因此可用三角函數模型進行描述.

思考 與盛水筒運動相關的量有哪些？它們之間有怎樣的關系？

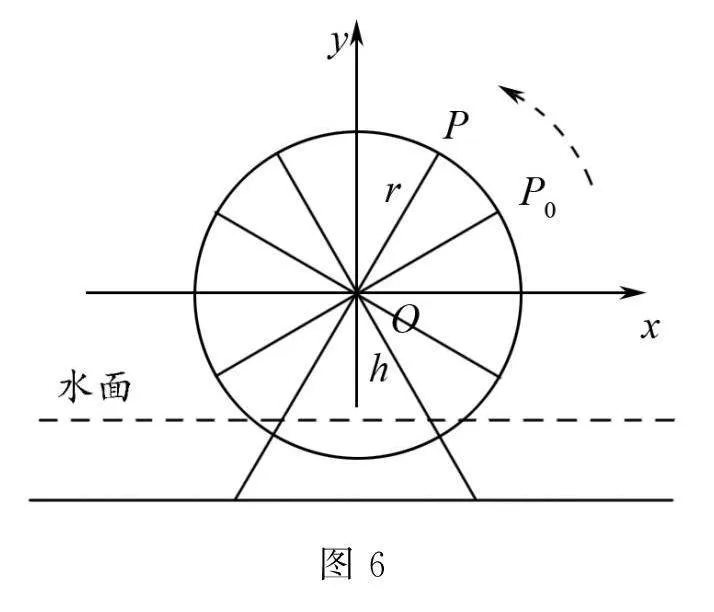
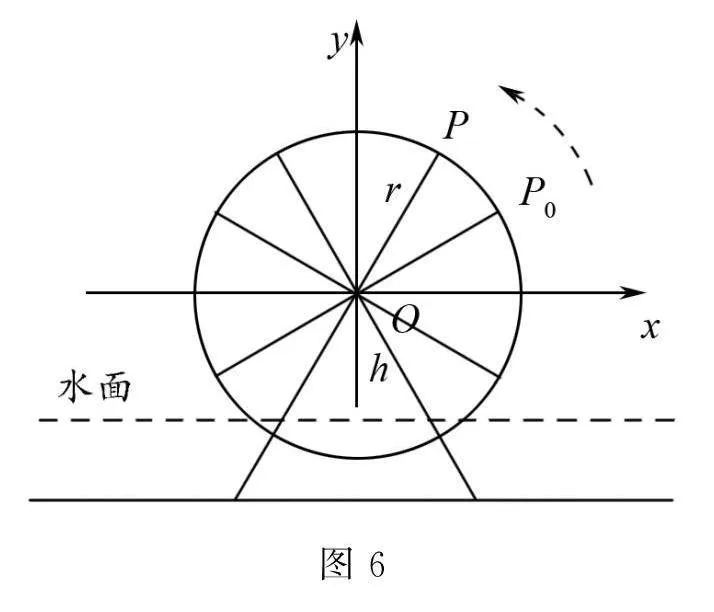
師生活動 學生小組合作交流后，進行成果展示.提煉總結出解析思路，建立三角函數模型.如圖6，設筒車轉輪的中心O到水面的距離為h，筒車的半徑為r，筒車轉動的角速度為ω，盛水筒的初始位置為P0以及所經過的時間為t.如圖，以O為原點，以與水平面平行的直線為x軸建立平面直角坐標系.設t=0時，盛水筒M位于點P0，以Ox為始邊，OP0為終邊的角為φ，經過時間t后運動到點Px，y，所以以Ox為始邊，OP為終邊的角為ωt+φ，有y=rsinωt+φ，所以盛水筒M距離水面的高度H與時間t的關系是H=rsinωt+φ+h.

設計意圖 學生逐步將現實問題轉化為過渡性數學問題，即將生活問題轉化為數學形式.

3 結語

大單元教學背景下的情境創設，為學生營造了探究性學習環境，引導其像學科專家般思考，實現深度學習.這一教學模式踐行了“學習即生活”的教育理念，值得在高中數學教學中推廣應用.

【基金項目：本文系廣東省教育科學規劃2023年度中小學教師教育科研能力提升計劃項目《基于情境與問題的高中數學課堂有效互動實施策略研究》（項目編號：2023YQJK332）的研究成果之一.】

參考文獻：

[1]毛瑞平.基于大單元教學的初中數學情境創設應用研究[D].山東師范大學，2024.

[2]丁智.大單元教學背景下高中數學教學情境創設研究[J].數理天地（高中版），2022（22）：41-43.

[3]黃屹.核心素養視域下的高中數學大單元教學設計探究[J].數理天地（高中版），2024（13）：99-101.

[4]朱琳.大單元教學中高中數學教學目標的制定[J].數理天地（高中版），2024（13）：61-63.

[5]吳凡.“三新”背景下高中數學大單元教學實施策略研究[J].考試周刊，2024（22）：88-91.