高中數(shù)學中問題鏈設(shè)計的原則與分類

【摘要】高中階段，正是學生在數(shù)學領(lǐng)域進行思維探索、全面發(fā)展自己的能力的最好時期，而問題鏈不僅為學生們搭建了數(shù)學學習的框架，也為培養(yǎng)學生高層次的思考創(chuàng)造了條件.結(jié)合人教A版數(shù)學教材，闡述在高中數(shù)學教學中，問題鏈的設(shè)計原則，包括目的性原則、趣味性原則、適度性原則和遞進性原則.并依據(jù)設(shè)計原則，將問題鏈分為多種類型，以引入型問題鏈、診斷型問題鏈和總結(jié)型問題鏈三種類型為例，具體說明問題鏈設(shè)計原則在問題鏈設(shè)計中的實際應用.

【關(guān)鍵詞】高中數(shù)學；問題鏈；數(shù)學教學

1 引言

在數(shù)學中，問題至關(guān)重要.哈爾莫斯曾說：“問題是數(shù)學的心臟”.眾多專家對此進行了深入研究.課堂教育中，以問題為核心，圍繞目標設(shè)計問題，推動課堂進程很重要.問題間應相互銜接，形成完整問題鏈.問題鏈是教師結(jié)合教學目標、內(nèi)容和學生學習情況，巧妙融合數(shù)學知識與問題，構(gòu)建的一系列相互關(guān)聯(lián)的數(shù)學問題.國內(nèi)知名的唐恒鈞和張維忠教授，在深入研究問題和問題教學的基礎(chǔ)上提出了問題鏈的概念，這一理念在數(shù)學教育界產(chǎn)生了廣泛的影響.他們認為，問題鏈是教師在課前精心準備，在課堂上以多種方式呈現(xiàn)給學生的有序問題序列，它不僅為學生提供了數(shù)學學習的基本框架，還為學生發(fā)展高級思維能力提供了可能[1].

2 問題鏈的設(shè)計原則

我國教育體系受儒家思想影響，強調(diào)啟發(fā)性教學.但當前課堂問題設(shè)計效果欠佳.問題鏈是新型教學理念，旨在通過系統(tǒng)、有目標的問題，師生共同感受數(shù)學抽象與邏輯推理之美.設(shè)計問題鏈需考慮教學目標、內(nèi)容和學生認知，遵循目的性、趣味性、適度性、遞進性等原則.

2.1 目的性原則

教師在設(shè)計問題鏈時，應確保問題服務于教學目標.基于教材，以教學目標為核心，明確教學重難點，并理解每個問題的目的：激發(fā)興趣、培養(yǎng)思考能力或檢驗知識.問題間應連貫，共同指向核心，逐步解決，直至得出最終答案.整個過程需圍繞教學目標，明確思考方向，避免無目的提問，如“是不是？對不對？”等.

比如在研究“函數(shù)單調(diào)性”時，可以這樣設(shè)計：請同學們判斷以下說法是否正確，并說明原因.（1）f（x）=x2是單調(diào)減函數(shù).（2）定義在R上的函數(shù)f（x）滿足f（1）<f（2），則它在R上是單調(diào)增函數(shù).（3）f（x）=x在定義域內(nèi)是單調(diào)函數(shù).每個問題都有背后的目的，圍繞教學目標和重難點，強調(diào)區(qū)間性及任意性，進而凸顯出概念的重要性，這種方式比純粹的文字強調(diào)要更有效.

2.2 趣味性原則

趣味性原則要求問題鏈的設(shè)計能夠吸引學生注意力.數(shù)學問題作為知識與生活的橋梁，教師應以興趣為導向，創(chuàng)設(shè)情景，讓學生成為探索者.設(shè)計貼近生活的問題鏈，利用媒體提高參與度.將實際問題轉(zhuǎn)化為數(shù)學公式，讓學生認識到數(shù)學無處不在.設(shè)計時需考慮學生能力和興趣，避免夸張案例.如“排列組合”教學中，可以這樣設(shè)計：邀請6名同學上臺（4男2女）.（1）他們排成一排有多少種排列方式？（2）若女生站一起，有幾種排列方式？（3）男生A不能站首位，女生不能站末位，又有幾種排列方式？這種設(shè)計與生活緊密相連，能調(diào)動課堂氛圍和促使學生思考.

2.3 適度性原則

在問題鏈設(shè)計中，需依據(jù)最近發(fā)展區(qū)理念，考慮問題的難易程度.中學階段，學生問答能力和知識儲備相對較弱.設(shè)計問題鏈時，要平衡難度與認知水平、實際能力.過易則缺乏思考，過難則影響信心與積極性.

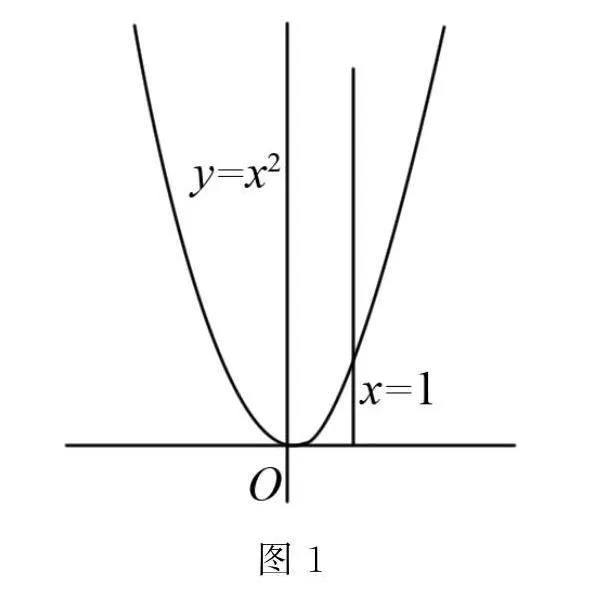
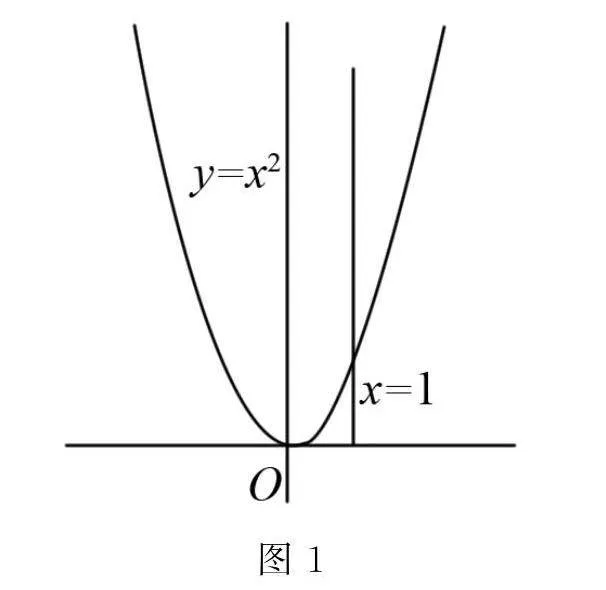
例如 在學習“導數(shù)的概念及其意義”時，可以如下設(shè)計：（1）請同學們回憶一下，我們是如何定義圓的切線的？（2）大家可以發(fā)現(xiàn)圓的切線是根據(jù)直線和圓的公共點來定義的，那么它適用于所有曲線嗎？（3）我們以y=x2為例，直線x=1與曲線y=x2僅有一個公共點，但它不是曲線的切線，因此不能用公共點的方式來定義，那么我們該如何給y=x2的切線下定義呢？（如圖1）先從學生比較熟悉的問題入手，避免他們產(chǎn)生挫N8gNbHqQEl7F6wRBrAf8eQ==敗感，接著提出有挑戰(zhàn)性的問題，引起他們的認知沖突，也讓他們的思維活躍起來，從而自然的引入求曲線切線的課題.

2.4 遞進性原則

遞進性原則強調(diào)在問題鏈設(shè)計中，教師應基于學生認知規(guī)律，逐步提出問題以促進其能力發(fā)展.數(shù)學知識構(gòu)建從簡單到復雜，師生對數(shù)學的理解也需由淺入深.設(shè)計問題鏈時，應遵循循序漸進原則，避免急躁.因?qū)W生能力各異，教師應調(diào)整問題鏈以適應不同需求.在中學數(shù)學教學中，教師應突破傳統(tǒng)觀念，以充分發(fā)揮問題鏈的指導與啟發(fā)作用.

例如 在完成“一元函數(shù)的導數(shù)及其應用”這一章的學習之后，進行練習時可以做如下設(shè)計：通過多媒體展示2023年新高考數(shù)學Ⅰ卷第19題“已知函數(shù)f（x）=a（ex+a）-x，討論f（x）的單調(diào)性”，并詢問（1）通過對試題題干的閱讀，你能獲取那些信息？（函數(shù)的定義域、導函數(shù)等）（2）我們學習了導數(shù)在研究函數(shù)中的應用，如何判斷f（x）的單調(diào)性呢？（判斷在某個區(qū)間內(nèi)導函數(shù)的正負，即可知道原函數(shù)在該區(qū)間內(nèi)的單調(diào)性）（3）針對這道題目，其中存在未知量a，應該如何進行單調(diào)性的討論呢？請同學們小組討論作答，并告知教師答案.通過上述由淺入深的問題，既可以幫助學生掌握導數(shù)在研究函數(shù)中的應用，感受數(shù)學分類討論的奧妙，也有助于培養(yǎng)學生的班級意識.

3 問題鏈的類型

課堂中教師提出的問題要符合學生的思維特點，最終目的是讓學生更好地學習數(shù)學，因此在課前預設(shè)好科學合理的問題鏈，對教學有很大幫助.依據(jù)設(shè)計原則，并分析課堂實際情況，可以將問題鏈分為引入型、總結(jié)型、診斷型、推廣型、探究型、差異型、一題多解型問題鏈.而本文將以引入型問題鏈、診斷型問題鏈和總結(jié)型問題鏈三種類型為例，具體說明問題鏈設(shè)計原則在問題鏈設(shè)計中的實際應用.

3.1 引入型問題鏈

引入是一堂課最重要的一環(huán)，具有承接新舊知識的功能.而顧名思義，引入型問題鏈的內(nèi)容可以是對之前所學的知識進行回顧，也可以是通過設(shè)置生活中的一些問題情景引入新課.但從實質(zhì)上講，引入型問題鏈是教師通過引入主題，為新內(nèi)容牽線搭橋，為后續(xù)的教學做鋪墊，激發(fā)學生的認知沖突或興趣，激發(fā)學生的好奇心而精心設(shè)置的問題鏈[2]REF_Ref220＼r＼h.要使學生對概念原理和規(guī)律的提出有一個直觀的認識，就要求學生建立起屬于自己的知識系統(tǒng)，熟練地掌握所學的知識，并通過類比、演繹、歸納等方式揭示新舊知識的聯(lián)系.引入型問題鏈多運用生動的案例、豐富多彩的情景、有趣又不乏深度的知識[3]REF_Ref15584＼r＼h.

例如 “基本不等式”這一節(jié)課，結(jié)合目的性和趣味性原則，可以設(shè)計如下問題鏈進行教學.

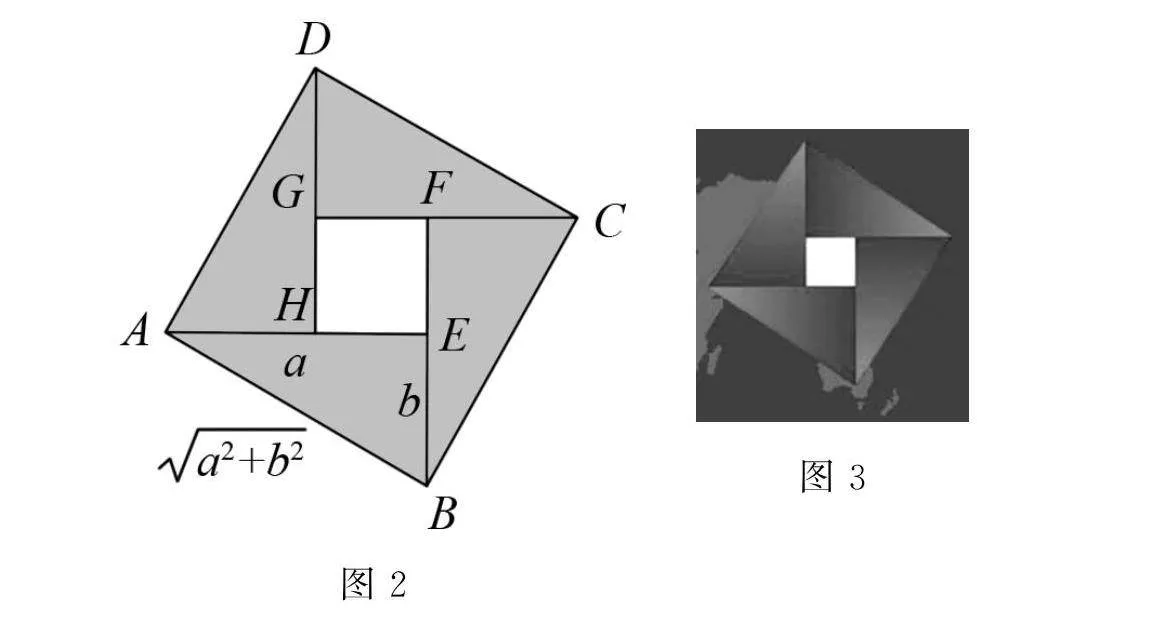
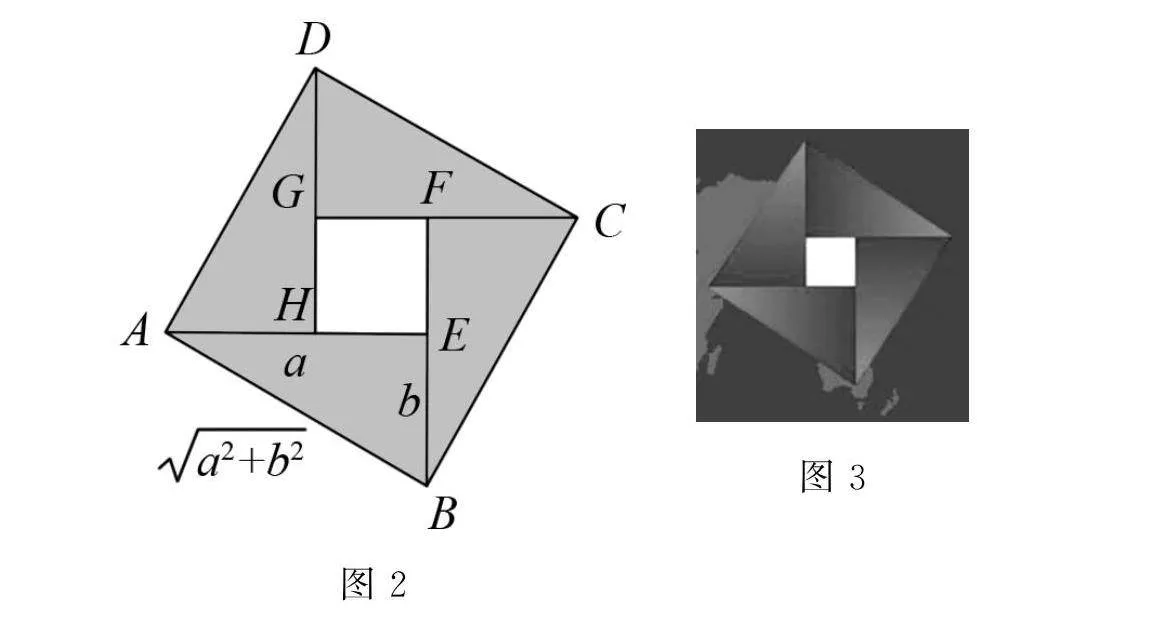
（1）請同學們看一下多媒體所呈現(xiàn)的圖形（圖2），這是在北京召開的第24屆國際數(shù)學家大會的會標，其是根據(jù)我國古代的趙爽弦圖設(shè)計的，是不是很像風車呢，我們將圖2中的風車抽象成數(shù)學模型（圖3），即在正方形ABCD中有4個全等的直角三角形，設(shè)直角三角形的兩條直角邊長分別為a，b，那么正方形ABCD的邊長為多少？正方形EFGH的邊長呢？你能從面積或其他角度入手，在圖3中找到“相等”關(guān)系嗎？

（2）同學們可以在圖3中找到“不等”關(guān)系嗎？（引導學生得到不等式a2+b2≥2ab）

（3）同學們想一想，這種“不等”關(guān)系什么時候可以取等號呢？（引導學生發(fā)現(xiàn)，當正方形EFGH縮為一個點時，取等號）

（4）用a、b替換a、b，我們可以得出何種不等關(guān)系？

教師利用多媒體給學生播放有關(guān)視頻和第24屆國際數(shù)學家大會會標并提問.對學生的回答進行總結(jié)歸納，并在黑板上展示不等關(guān)系的數(shù)學表達式.在教師的引導下，學生可以在觀察的過程中，歸納出圖形中的相等關(guān)系以及不等關(guān)系.最終可以得到不等式a2+b2≥2ab進而引入新課——基本不等式.

3.2 診斷型問題鏈

診斷型問題鏈是圍繞教學重點、難點、疑點和易錯點設(shè)計的問題序列.它鼓勵學生犯錯并找出原因，保持對數(shù)學的好奇與興趣，防止學生輕視數(shù)學，提升課堂參與度.這有助于學生發(fā)展數(shù)學反思能力，并允許教師基于學生錯誤進行有針對性的教學改進.簡而言之，診斷型問題鏈使學生在錯誤中學習和成長.

例如 “等差數(shù)列”的課程安排位于“數(shù)列的基本概念”后，作為重要的數(shù)學模型，其研究方式普遍，并為等比數(shù)列學習打下基礎(chǔ).因此，在數(shù)列章中地位極為重要.講授時，可結(jié)合適度性原則，設(shè)計以下問題鏈：

小王同學背單詞時，他的詞匯量只有16個單詞，他想要改變這一現(xiàn)狀，于是下定決心從下周開始，每周背熟15個新單詞，如果他能堅持下去，請問：

（1）小王在兩個月后期中考試時能記住多少單詞？

（2）按照這樣的速度，小王能否達成期末要求的500個單詞的詞匯量要求？

引導學生以數(shù)字的形式，列出小王同學詞匯量增加的數(shù)列：16，31，46，61，76，91……

列出數(shù)列后，學生易發(fā)現(xiàn)規(guī)律解決第一個問題.但第二個問題學生可能遇阻并出錯.針對錯誤，教師診斷并引導學生思考，使學生保持學習興趣.通過生活實例引入等差數(shù)列，讓學生感受數(shù)學與生活的緊密聯(lián)系，認識數(shù)學的重要性.設(shè)置適當難度問題，激發(fā)學生學習興趣.

3.3 總結(jié)型問題鏈

總結(jié)型問題鏈用于知識點或單元總結(jié)，幫助學生回憶所學，構(gòu)建系統(tǒng)知識結(jié)構(gòu)，反思學習成果.通過整合內(nèi)容，歸納零散知識，形成知識網(wǎng)絡(luò)，提升獨立思考能力.回顧鞏固所學，增強解題成就感，激發(fā)學習熱情.數(shù)學作為研究性學科，需深入研究如何提高教學質(zhì)量，利用問題鏈來提升學習能力.

例如 在“數(shù)列”這一章節(jié)進行復習教學時可以結(jié)合遞進性原則做如下設(shè)計，教師利用多媒體，給學生展示如下總結(jié)型問題鏈.

（1）請同學們回憶一下數(shù)列的基本概念.

（2）你能想出生活中有關(guān)數(shù)列的例子嗎？

（3）等差數(shù)列和等比數(shù)列，分別有什么樣的特點？通項公式又是怎樣的？怎么求各項的和呢？

總結(jié)型問題鏈是以上面提到的數(shù)列總結(jié)型問題鏈為例，結(jié)合遞進性原則而設(shè)置的有序且遞進的問題鏈，不是平行的可以隨意作答的問題，因此，教師在引導學生作答的過程中，要根據(jù)多媒體給出問題的順序，逐個擊破，讓學生們感受數(shù)學層層遞進的性質(zhì).

4 結(jié)語

問題鏈教學法是一種行之有效的方法，它可以提高中學數(shù)學課堂的教學效率，提高學生的學習興趣.問題鏈是引導學生思考的路標，數(shù)學知識以問題鏈的方式嵌入在教學過程中，能有效地促進教師和學生的共同成長，是教學與學習之間的一座橋梁.通過問題鏈教學，可以很好地完成新舊知識的傳遞和能力的提升.問題鏈能促進教學模式的革新、學習方式的革新、教師主導性和學生主體性的有效發(fā)揮.在教學實踐中，問題鏈可以幫助學生更好地理解與掌握知識，培養(yǎng)他們的思維能力，達到預期目標.

參考文獻：

[1]唐恒鈞，張維忠.數(shù)學問題鏈教學的理論與實踐[M].上海：華東師范大學出版社，2021.

[2]王培峰. 基于問題鏈教學培養(yǎng)高中生化學高階思維的實踐研究[D].山西師范大學，2023.

[3]王露萍.試論化學教學中“問題鏈”的設(shè)計[J].化學教學，2011（03）：6-10.

[4]陳小璐.合理設(shè)計“問題鏈”環(huán)環(huán)相扣提素養(yǎng)——以“概率中的遞推數(shù)列”教學設(shè)計為例[J].高中數(shù)學教與學，2024（11）：1-4+26.

[5]蔣曉清.基于“問題鏈”的高中數(shù)學教學實踐——以圓的標準方程為例[J].中學數(shù)學，2024（09）：128-129.