應(yīng)用于空中平臺主動防御作戰(zhàn)軌跡預(yù)測過程的狀態(tài)估計方法研究

摘 要：從主動防御的實際作戰(zhàn)需求入手， 分析軌跡預(yù)測不同方法的優(yōu)缺點及使用場景， 分析空中平臺主動防御作戰(zhàn)場景相較于目前主要研究的其他飛行器軌跡預(yù)測場景的區(qū)別， 針對該場景下軌跡預(yù)測對象特殊的攻擊意圖和運動規(guī)律提出一種基于擴展卡爾曼濾波的狀態(tài)估計方案。 基于仿真軟件模擬了攻擊彈以比例導(dǎo)引攻擊載機的過程， 以滿足比例導(dǎo)引系數(shù)不變的條件建立觀測模型， 采用擴展卡爾曼濾波為非線性的模型進行線性化仿真， 觀測到不同時刻攻擊彈的運動狀態(tài)， 并以此進行短時間的軌跡預(yù)測。 仿真結(jié)果表明， 該模型在主動防御作戰(zhàn)場景下能顯著減小狀態(tài)估計誤差。

關(guān)鍵詞：空空導(dǎo)彈； 主動防御； 三體對抗； 軌跡預(yù)測； 狀態(tài)估計； 擴展卡爾曼濾波

中圖分類號： TJ765.4

文獻標(biāo)識碼： A

文章編號：1673-5048（2024）04-0041-08

DOI： 10.12132/ISSN.1673-5048.2023.0251

0 引 言

目前， 空中平臺主要依靠逃逸機動、 電磁干擾等手段應(yīng)對敵方空空導(dǎo)彈的威脅， 然而在存在干擾的情況下， 空空導(dǎo)彈的命中率仍能達到50％～60％， 亟待發(fā)展新的防御手段來提升空中平臺的生存能力。 歐美已經(jīng)開始發(fā)展攔截來襲導(dǎo)彈的空中平臺主動防御技術(shù)［1-2］， 通過“硬殺傷”的手段對來襲導(dǎo)彈進行攔截。 來襲空空導(dǎo)彈的飛行馬赫數(shù)能夠達到3以上， 攔截彈與目標(biāo)的交會馬赫數(shù)可以達到6～7， 需要迎頭小角度交會才能形成有效的毀傷時間窗口［3］。 因此， 空中平臺攔截彈需要在保證制導(dǎo)精度的同時， 滿足末端彈目交會角度約束。

目標(biāo)的識別和狀態(tài)估計過程存在誤差， 而且空空導(dǎo)彈具備較高的機動能力， 機動過載最高可達50g［4］， 傳統(tǒng)的制導(dǎo)方法直接將攔截對象作為跟蹤目標(biāo)進行交會角度約束制導(dǎo)時， 需要頻繁變更過載大小及方向， 又因為觀測誤差和目標(biāo)機動的影響， 實時保持約束跟蹤目標(biāo)對能量的消耗很大， 且很難實現(xiàn)交會角約束， 因而目前交會角約束制導(dǎo)律的研究多為通過軌跡預(yù)測得到虛擬目標(biāo)或虛擬碰撞點通過跟蹤虛擬對象的方法進行制導(dǎo)律設(shè)計［5-9］， 或在目標(biāo)運動狀態(tài)可預(yù)測的前提下［10］使用最優(yōu)制導(dǎo)［11-13］， 以滿足約束條件并減小脫靶量和能量消耗。 實際情況下， 對來襲導(dǎo)彈的探測過程存在各種噪聲， 因此減小噪聲影響并準(zhǔn)確預(yù)測來襲導(dǎo)彈的運動軌跡， 是空中平臺主動防御武器制導(dǎo)律設(shè)計的重要條件。

目前關(guān)于飛行器軌跡預(yù)測的研究對象多為飛機、 彈道導(dǎo)彈和高超聲速飛行器等， 針對空空導(dǎo)彈軌跡預(yù)測研究較少。 本文針對空中平臺主動防御作戰(zhàn)場景， 結(jié)合現(xiàn)有其他場景下軌跡預(yù)測的研究方法， 提出一種基于擴展卡爾曼濾波的來襲導(dǎo)彈空空導(dǎo)彈狀態(tài)估計模型， 并通過仿真驗證了方法的有效性。

1 軌跡預(yù)測方法與場景的分析

飛行器軌跡預(yù)測方法設(shè)計主要分為三步［14］： （1）識別目標(biāo)的運動特征； （2）跟蹤目標(biāo)的運動狀態(tài)； （3）根據(jù)目標(biāo)運動狀態(tài)外推進行軌跡預(yù)測， 同時根據(jù)目標(biāo)信息是否透明分為合作型目標(biāo)和非合作型目標(biāo)。

識別目標(biāo)運動特征， 意在減小目標(biāo)軌跡預(yù)測的范圍， 精確化軌跡預(yù)測的模型。 目前的研究方案分為3種： 基于計算流體力學(xué)模型的分析［15-16］、 基于風(fēng)洞試驗?zāi)Ｐ偷姆治觯?7］、 基于動力學(xué)方程和運動方程的目標(biāo)軌跡分析［18-19］。 前兩種方案屬于針對合作型目標(biāo)的運動特征識別方法， 第三種方案屬于針對非合作型目標(biāo)的運動特征識別方法。 作為非合作型目標(biāo)， 空空導(dǎo)彈類目標(biāo)受力復(fù)雜且動力充足， 基于運動學(xué)方程和運動方程的目標(biāo)運動特征分析更具可行性。

目標(biāo)運動狀態(tài)估計分為兩類， 以動力學(xué)模型為基礎(chǔ)的狀態(tài)估計和以運動學(xué)模型為基礎(chǔ)的狀態(tài)估計。 基于動力學(xué)模型的狀態(tài)估計常用于空間飛行器的狀態(tài)估計研究， 因為目標(biāo)機動能力較弱， 受力分析相較于其他場景較為簡單。 基于運動學(xué)模型的狀態(tài)估計多用于存在特定運動規(guī)律的目標(biāo)， 其本質(zhì)是針對目標(biāo)運動進行統(tǒng)計學(xué)分析而總結(jié)出目標(biāo)的機動規(guī)律。 基于觀測過程中引入干擾的不同分為白噪聲模型和有色噪聲模型， 本文研究的白噪聲問題模型為恒定加速度模型（Constant Acceleration， CA）［20］和勻速轉(zhuǎn)彎模型（Constant Turn， CT）［21］。 這兩種模型分別把目標(biāo)運動視為瞬時的勻加速運動和勻速圓周運動， 通過卡爾曼濾波等方法將觀測數(shù)據(jù)擬合到對應(yīng)的運動軌跡中減小噪聲影響， 估計出較為準(zhǔn)確的狀態(tài)信息和運動規(guī)律。 雖不同于飛機類目標(biāo)存在特定運動模式（CA， CT）， 空空導(dǎo)彈的運動服從特定制導(dǎo)律的控制， 理論上仍可通過運動學(xué)模型進行狀態(tài)估計。

目標(biāo)軌跡的預(yù)測方法有解析法、 幾何法和數(shù)值積分法3種類型。 解析法用于機動能力弱或無機動能力的目標(biāo)， 如彈道導(dǎo)彈被動段［22］， 通過帶入狀態(tài)信息到特殊的函數(shù)里得到準(zhǔn)確的預(yù)測結(jié)果， 而在目標(biāo)機動能力較強的情況下無法得到準(zhǔn)確的解析解。 幾何法通過對目標(biāo)的運動軌跡進行分析， 使其擬合于一條特定的曲線［23］。 該方法計算速度快、 短時精確度高、 長時間的精確度根據(jù)不同研究場景差異度不同。 數(shù)值積分法用于合作類目標(biāo)或信息透明度很高的非合作目標(biāo)。 該方法需要對目標(biāo)進行精確的運動模型建模分析， 以及準(zhǔn)確的發(fā)動機動力和氣動力分析， 并對其加速度進行積分［24］， 而在攔截作戰(zhàn)場景下預(yù)測目標(biāo)的氣動參數(shù)無法獲取， 故無法進行精確計算， 該方法局限性較大。 除此之外， 隨著計算機科技的發(fā)展， 人工智能算法也被逐步應(yīng)用到飛行器軌跡預(yù)測領(lǐng)域， 如神經(jīng)網(wǎng)絡(luò)和深度學(xué)習(xí)等方法［25-26］， 但均需要大量的歷史數(shù)據(jù)作為支撐， 且對目標(biāo)大機動場景預(yù)測效果一般的同時， 很難滿足快速性的需求。

目前關(guān)于軌跡預(yù)測的研究中， 針對第三步軌跡預(yù)測的研究方法有很多， 但或是基于目標(biāo)當(dāng)前運動狀態(tài)完全已知的假設(shè)， 或是在第二步狀態(tài)估計過程使用了基于卡爾曼濾波的CA或CT簡單模型或多模型融合進行狀態(tài)估計， 并沒有從觀測模型本身進行改進。 目標(biāo)狀態(tài)估計的準(zhǔn)確性作為軌跡預(yù)測的前置條件的同時， 還直接決定了制導(dǎo)律設(shè)計時脫靶量的理論最小值。 本文針對狀態(tài)估計過程中的卡爾曼濾波模型， 結(jié)合空中平臺主動防御作戰(zhàn)的特點， 設(shè)計出符合該場景下運動特征的狀態(tài)估計模型。

空中平臺主動防御問題也稱為三體對抗（Target- Attacker-Defender， TAD）問題， 最早由Boyell提出［27］， 該場景由攻防兩方至少三個或以上的飛行器組成， 即攻擊彈（Attacker， A）以防御方空中平臺（Target， T）為目標(biāo)進行攻擊， 防御方空中平臺以逃逸為目標(biāo)， 防御方攔截彈（Defender， D）以攔截攻擊方空空導(dǎo)彈為目標(biāo)。 該場景有如下幾個特點：

（1） 大多數(shù)空空導(dǎo)彈發(fā)動機工作時間為10 s左右， 最多不超過30 s， 有效作戰(zhàn)半徑在百公里內(nèi)［28］， 因此空中平臺主動防御作戰(zhàn)時間較短， 針對來襲導(dǎo)彈的作戰(zhàn)意圖分析相比于飛機、 彈道導(dǎo)彈、 超高聲速飛行器類目標(biāo)更為精確， 同時目標(biāo)作戰(zhàn)意圖明確， 即攻擊我方載機。

（2） 攻擊彈機動能力強且為非合作目標(biāo)， 無法應(yīng)用解析法和數(shù)值積分法進行預(yù)測。 比例導(dǎo)引律控制下的攻擊彈（空空導(dǎo)彈和面空導(dǎo)彈）運動與我方載機的運動具有強相關(guān)性。

（3） 載機是合作飛行器， 我方載機未來的飛行軌跡是可控制和可預(yù)測的。

在主動防御作戰(zhàn)過程中， 攻擊彈的位置信息觀測結(jié)果由空中平臺、 防御方攔截彈和預(yù)警機等多個平臺數(shù)據(jù)融合得到， 觀測誤差較為復(fù)雜。 為方便研究， 本文將融合后的位置信息噪聲簡化為縱橫坐標(biāo)上滿足高斯分布的白噪聲。 基于以上特點， 針對目標(biāo)觀測過程中的白噪聲， 本文提出一種在軌跡預(yù)測過程中引入我方載機位置信息的預(yù)測模型， 即基于擴展卡爾曼濾波的導(dǎo)航比（Constant Proportional Navigation Ratio， CPNR）固定的運動學(xué)預(yù)測模型。

不同于傳統(tǒng)的以攔截目標(biāo)作為軌跡預(yù)測過程單一研究對象的預(yù)測方案， 本文使用一種新的狀態(tài)估計模型。 其核心思想是將載機運動信息和攻擊彈位置觀測信息同時作為已知信息進行輸入， 考慮到觀測過程引入的位置信息噪聲， 借由載機運動與攻擊彈運動的高度耦合性以減小狀態(tài)估計和軌跡預(yù)測過程的誤差。 將載機與攻擊彈的相對運動信息通過擴展卡爾曼濾波線性化擬合到比例導(dǎo)引軌跡上， 對觀測環(huán)節(jié)引入的白噪聲進行濾波， 得到其運動狀態(tài)和運動規(guī)律（導(dǎo)航比）， 并通過載機未來的運動趨勢來預(yù)測攻擊彈的運動軌跡。

2 軌跡預(yù)測算法

2.1 狀態(tài)估計模型

本文使用二維簡化模型， 假設(shè)載機T的運動和來襲導(dǎo)彈A的運動發(fā)生在同一攻擊平面內(nèi)。 假設(shè)攻擊彈的控制環(huán)節(jié)無延遲， 其姿態(tài)始終朝向速度方向， 且加速度始終與速度方向垂直， 即速度模值保持不變， 以導(dǎo)航比不變的比例導(dǎo)引律追擊我方載機。 坐標(biāo)系選取地面坐標(biāo)系， 坐標(biāo)原點設(shè)在攻擊彈在地面的投影處， 如圖1所示。

在主動防御作戰(zhàn)時， 進攻方攻擊彈的導(dǎo)航比對于防御方來說是未知的， 因此選取如下狀態(tài)變量： x1為攻擊彈在x軸上的坐標(biāo)； x2為攻擊彈在z軸上的坐標(biāo)； x3為攻擊彈的速度角； x4為攻擊彈的速度模值； x5為攻擊彈的導(dǎo)航比。

主動防御作戰(zhàn)場景中載機為合作單位， 空戰(zhàn)機動動作基本固定， 因而其短時間內(nèi)的運動狀態(tài)完全透明且可預(yù)知， 因此其位置信息可以作為軌跡預(yù)測過程的輸入變量， 即u1為載機在x軸上的坐標(biāo)； u2為載機在z軸上的坐標(biāo)； 而攻擊彈在坐標(biāo)軸上的真實位置為輸出變量， 即y1為攻擊彈在x軸上真實位置； y2為攻擊彈在z軸上真實位置。

假設(shè)離散系統(tǒng)的采樣周期為Ts， 其速度角θA和彈目視線角qA狀態(tài)滿足以下關(guān)系：

θA， k－θA， k－1=N（qA， k－1－qA， k－2）（1）

即

x3， k=x3， k－1+x5（qA， k－1－qA， k－2）（2）

其中， qA， k=arctanu2， k－x2， ku1， k－x1， k。

攻擊彈運動學(xué)Xk=f（Xk－1， Uk－1）方程為

Xk=Xk－1+x4， k－1cos（x3， k－1）Tsx4， k－1sin（x3， k－1）Tsx5， k－1（qA， k－1－qA， k－2）00（3）

Yk=1000001000Xk（4）

2.2 擴展卡爾曼濾波軌跡預(yù)測

2.2.1 運動參數(shù)估計

防御方觀測到的攻擊彈在坐標(biāo)軸上的位置設(shè)置為： z1為攻擊彈在x軸上觀測位置； z2為攻擊彈在z軸上觀測位置； v1為x軸上觀測過程引入的服從N（0， r1）的誤差值； v2為x軸上觀測過程引入的服從N（0， r2）的誤差值。

z1=y1+v1z2=y2+v2 （5）

攻擊彈的非線性系統(tǒng)狀態(tài)估計方程表達式為

Zk=HXk－1+VkXk=f（Xk－1， Uk－1） （6）

（1） 先驗估計

X^-k=f（X^k-1， Uk-1）

P-k=AkPk-1ATk （7）

式中： X^-k和P－k分別為狀態(tài)變量和狀態(tài)協(xié)方差矩陣的先驗估計值； Ak矩陣為雅可比矩陣， 即

Ak=JF（x1， x2， x3， x4， x5）|X=

（x^1， k， x^2， k， x^3， k， x^4， k， x^5， k）T=

10x1x3x1x4001x2x3x2x40x3x1x3x210x1x50001000001|X=X^k－1（8）

代入X=X^k－1， 矩陣各元素如下：

x1x3|（X=X^k－1）=－x^4， k－1sin（x^3， k－1）Ts

x1x4|（X=X^k－1）=cos（x^3， k－1）Ts

x2x3|（X=X^k－1）=x^4， k－1cos（x^3， k－1）Ts

x2x4|（X=X^k－1）=sin（x^3， k－1）Ts

x3x1|（X=X^k－1）=x^5， k－1（u2， k－1－x^2， k－1）（u1， k－1－x^1， k－1）2+（u2， k－1－x^2， k－1）2

x3x2|（X=X^k－1）=－x^5， k－1（u1， k－1－x^1， k－1）（u1， k－1－x^1， k－1）2+（u2， k－1－x^2， k－1）2

x3x5|（X=X^k－1）=arctanu2， k－1－x^2， k－1u1， k－1－x^1， k－1－

arctanu2， k－2－x^2， k－2u1， k－2－x^1， k－2 （9）

（2） 后驗估計

Kk=PkHT（HPkHT+R）-1

X^k=X^-+Kk（Zk-HX^-）

Pk=（I-KkH）P-k（10）

式中： Kk為卡爾曼增益； X^k， Pk分別為狀態(tài)后驗估計值和協(xié)方差矩陣； R為觀測噪聲協(xié)方差矩陣， R=r100r2； H為觀測矩陣， H=1000001000。

2.2.2 軌跡預(yù)測

本文使用的軌跡預(yù)測方法， 屬于幾何法的范疇。 在迭代計算出攻擊彈的運動參數(shù)后， 將運動參數(shù)和我方載機未來的位置信息代入運動方程（3）和（4）中進行多次迭代， 預(yù)測出一段時間以后的坐標(biāo)軸位置。

3 仿真實驗

3.1 仿真條件

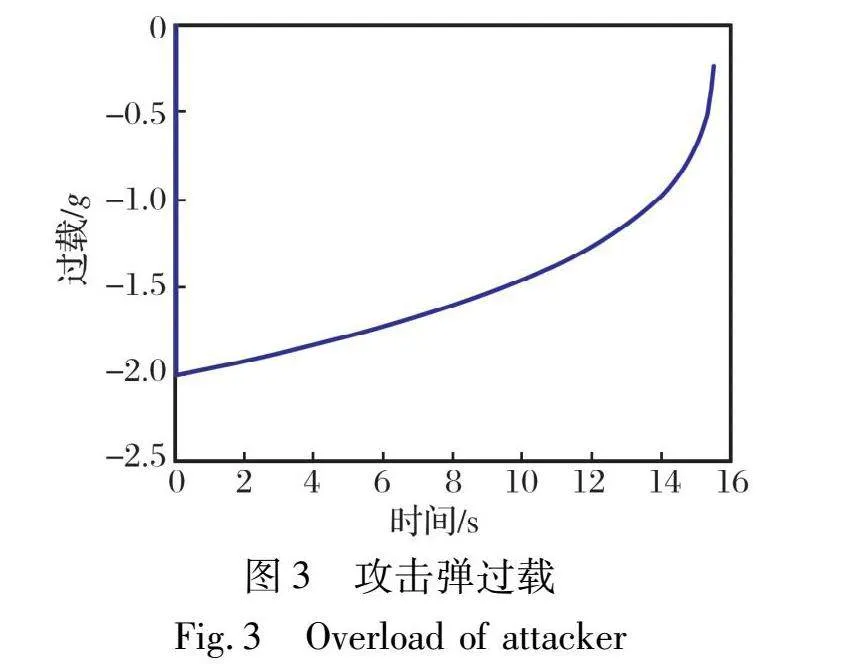
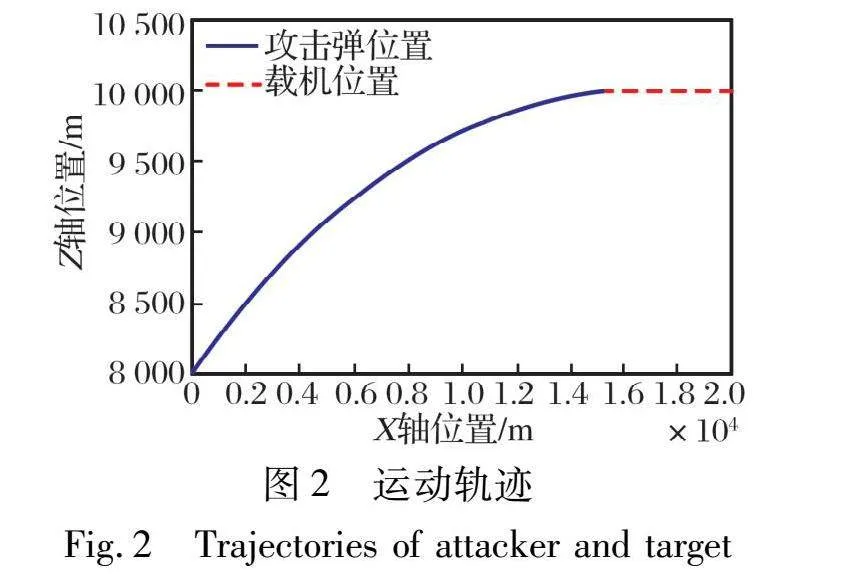
初始時刻， 載機位于坐標(biāo)軸（20 000， 10 000）點， 攻擊彈位于（0， 8 000）點。 載機保持水平向x軸負(fù)方向以300 m/s速度勻速直線飛行， 攻擊彈初始速度角為15°， 保持速度為1 000 m/s， 以比例系數(shù)為3的比例導(dǎo)引追擊載機， 其控制系統(tǒng)不存在時間延遲， 仿真步長選擇Ts=0.001 s， 仿真過程中忽略重力作用。 根據(jù)式（3）～（4）仿真得到導(dǎo)彈追擊載機的軌跡圖， 如圖2所示。 導(dǎo)彈全機動過程的過載如圖3所示。

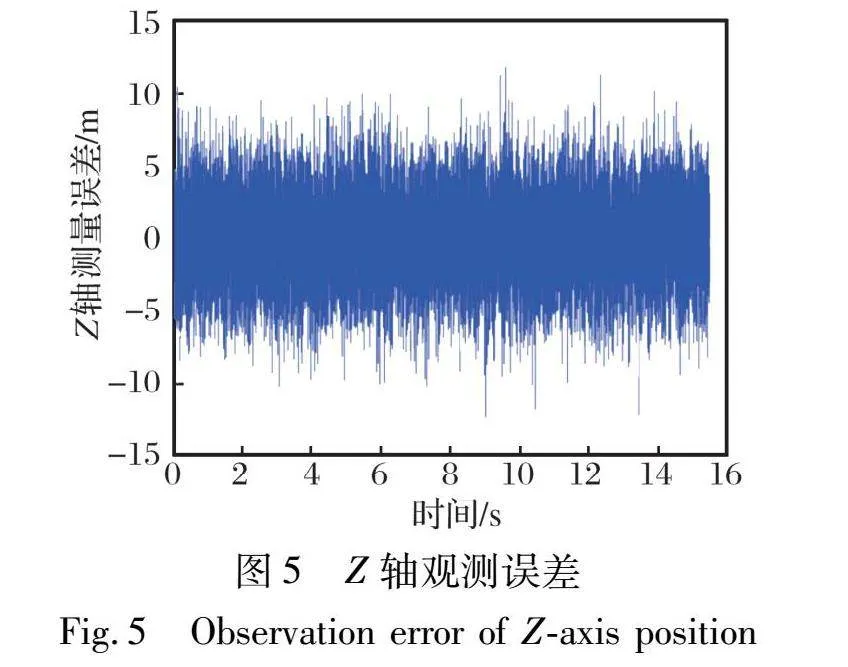
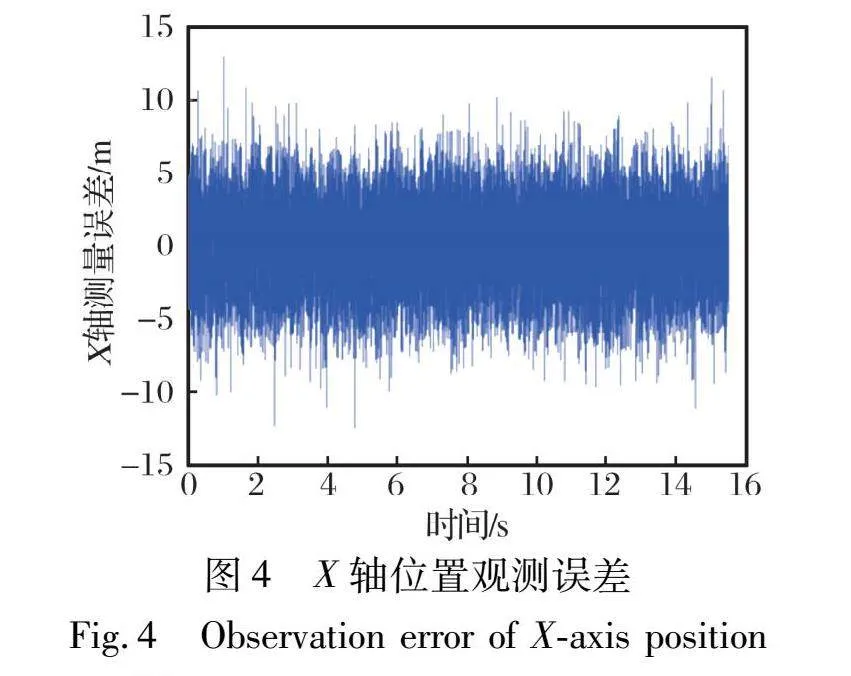
假設(shè)只存在觀測噪聲而不存在過程噪聲， 觀測值為攻擊彈的縱橫坐標(biāo)位置， 觀測噪聲為均值0方差9的高斯噪聲。 觀測誤差如圖4～5所示。

3.2 仿真數(shù)據(jù)

3.2.1 技術(shù)指標(biāo)

假設(shè)載機最大可承受過載為5g， 載機在6 s時由原有的直線運動轉(zhuǎn)為向上做最大過載下的筋斗動作。 假設(shè)預(yù)計10 s時完成攔截， 在6 s時防御方攔截彈已經(jīng)形成迎頭攻擊態(tài)勢。 防御方攔截彈將根據(jù)剩余時間的變化同步減少軌跡預(yù)測時間， 以更新預(yù)計碰撞點最終在載機機動后的真實碰撞點完成攔截。 在此過程中， 脫靶量理論最小值同時受制于長時間的預(yù)測誤差和預(yù)計命中時間的目標(biāo)狀態(tài)估計誤差。

以6 s為仿真開始時間， 對攻擊彈未來4 s的真實軌跡與預(yù)測軌跡進行仿真， 仿真軌跡包括載機維持原有運動狀態(tài)的情況下6～10 s過程中攻擊彈真實的運動軌跡、 載機機動狀態(tài)改變的情況下6～10 s過程中攻擊彈真實的運動軌跡、 6 s時以載機運動狀態(tài)未改變?yōu)榧僭O(shè)得到的未來4 s的攻擊彈預(yù)測軌跡。 在載機運動狀態(tài)改變的瞬間會造成攻擊彈真實軌跡與運動狀態(tài)未改變時含誤差的預(yù)測軌跡之間產(chǎn)生較長距離的偏移。 為了保證4 s后防御方攔截彈能夠準(zhǔn)確命中攻擊彈， 軌跡預(yù)測的誤差存在一個可初步計算的指標(biāo)。

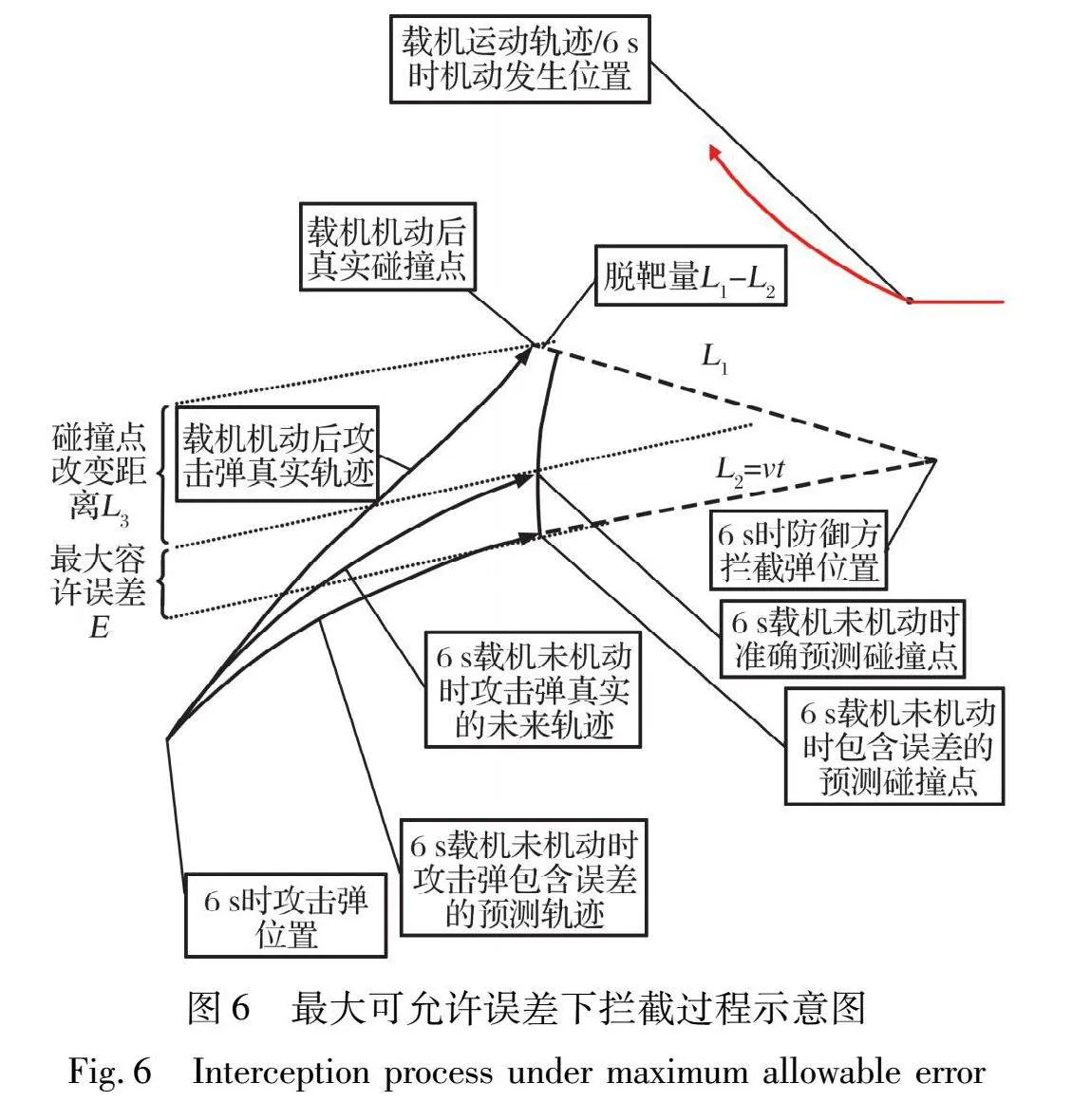
攔截過程的示意圖如圖6所示。

圖中， L1為6 s時防御方攔截彈位置與載機機動后真實碰撞點的距離； L2為6 s時防御方攔截彈位置與含誤差的載機機動前預(yù)測碰撞點的距離； L3為真實預(yù)測碰撞點改變的距離； v為防御方攔截彈的速度模值， v=800 m/s； t為攔截過程剩余時間， t=4 s。

（L3+E）2+L22≈L21L1－L2<5L2=vt （11）

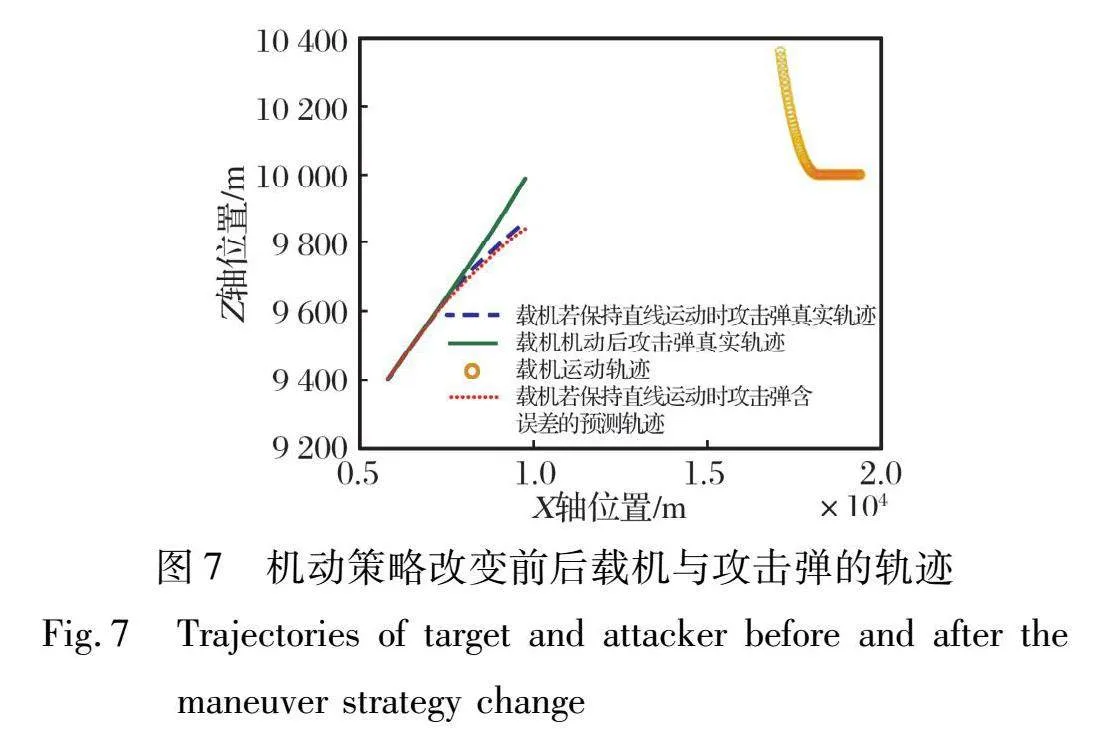
載機和攻擊彈的位置仿真結(jié)果如圖7所示。

由仿真結(jié)果可得真實碰撞點的坐標(biāo)（7 791.0， 9 779.9）， 載機未機動時準(zhǔn)確預(yù)測碰撞點的坐標(biāo)（7 808.4， 9 673.5）， 將位置坐標(biāo)信息代入到式（11）中求得E的限制條件， 得到在此場景下6～10 s進行對攻擊彈的攔截， 則脫靶量小于3 m的前提是， 需保證4 s預(yù)測時間間隔的預(yù)測誤差E<30.7 m， 且預(yù)計命中點位置估計誤差小于3 m。

3.2.2 仿真結(jié)果

目前， 以導(dǎo)彈為軌跡預(yù)測對象的多模型預(yù)測算法中去除高斯分布觀測噪聲時， 常用的模型為CA和CT模型， 其中CA模型為線性濾波模型， CT模型為非線性濾波模型。 因整個過程中攻擊彈的運動規(guī)律并未發(fā)生改變， 故本文將CPNR模型直接與CA和CT模型進行對比。

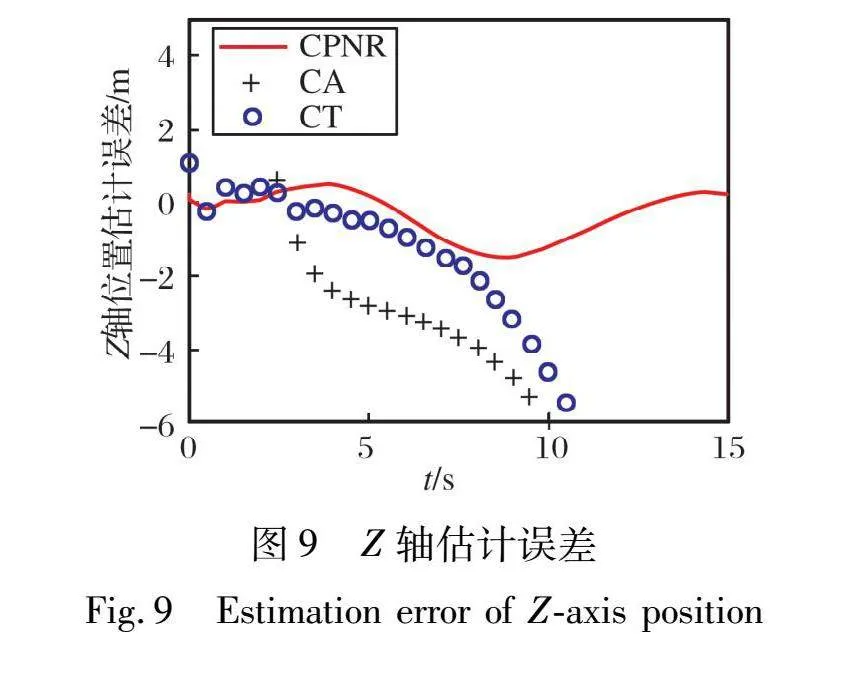
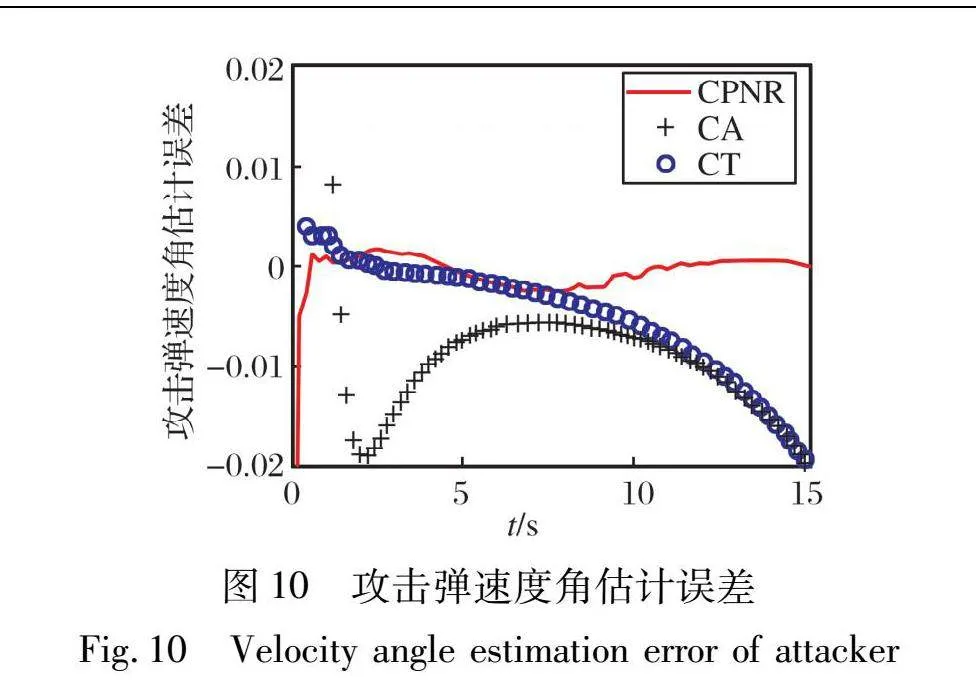
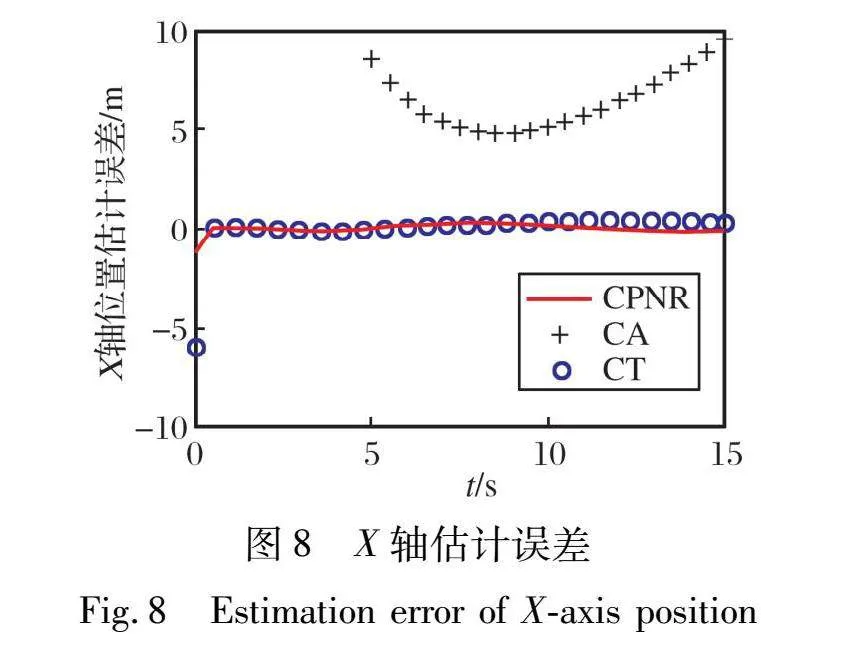
將攻擊彈位置觀測值代入到式（7）和式（10）中實時迭代， 進行對攻擊彈各個狀態(tài)變量的估計， 其位置與速度狀態(tài)估計值誤差與CA和CT模型狀態(tài)估計誤差的對比如圖8～11所示。 導(dǎo)航比估計值如圖12所示。

由圖8～12可知， 導(dǎo)航比固定的擴展卡爾曼濾波可以很好地跟蹤攻擊彈的運動狀態(tài)。

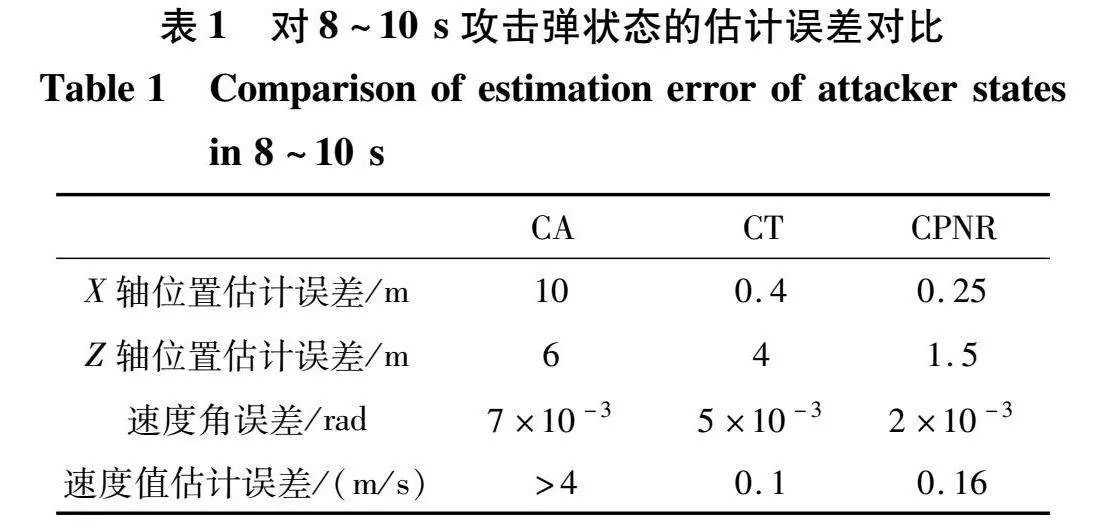
一般情況下， 防御方攔截彈速度略小于攻擊彈， 以防御方攔截彈的發(fā)射時間為起點， 攻擊彈預(yù)計命中載機時間為終點， 攔截過程發(fā)生在攻擊過程的后半段。 在假設(shè)的仿真條件下， 攻擊彈將于15 s以后命中載機， 因此將攔截時間假設(shè)為8～10 s之間， 此時三種模型的狀態(tài)估計誤差對比如表1所示。

由表1可知， 在本文仿真假設(shè)條件下， 使用CT模型對攻擊彈進行狀態(tài)估計時， 位置誤差最大可達4 m， 此時防御方攔截彈的脫靶量很難控制在4 m以內(nèi)， 而CPNR模型的位置估計誤差遠(yuǎn)小于CA和CT模型， 最大脫靶量在1.5 m左右， 且速度角估計誤差也小于另外兩個模型， 這就決定了在進行第三步軌跡預(yù)測時會有更小的預(yù)測誤差， 同時在碰撞角度約束時更加精確。

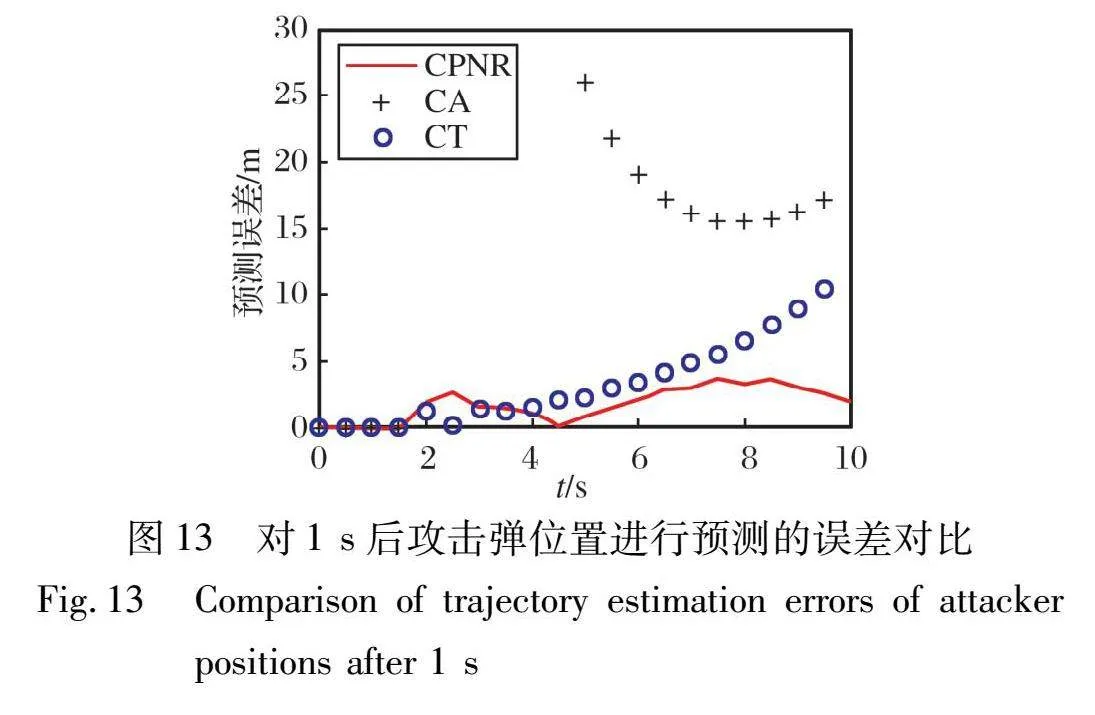
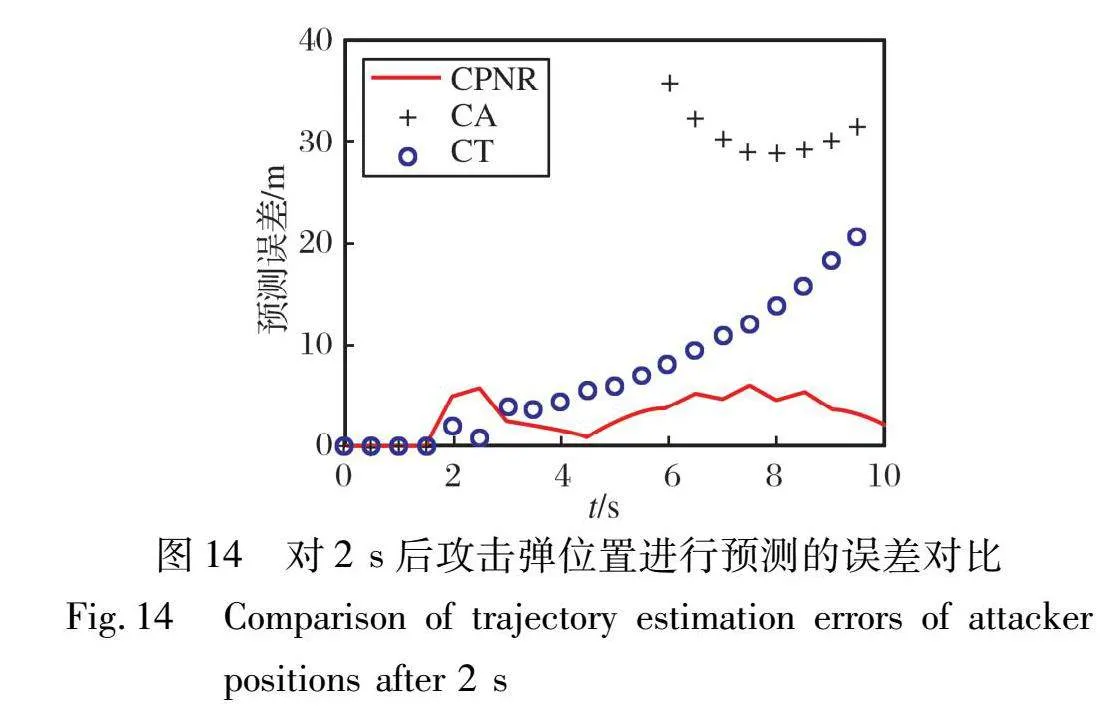
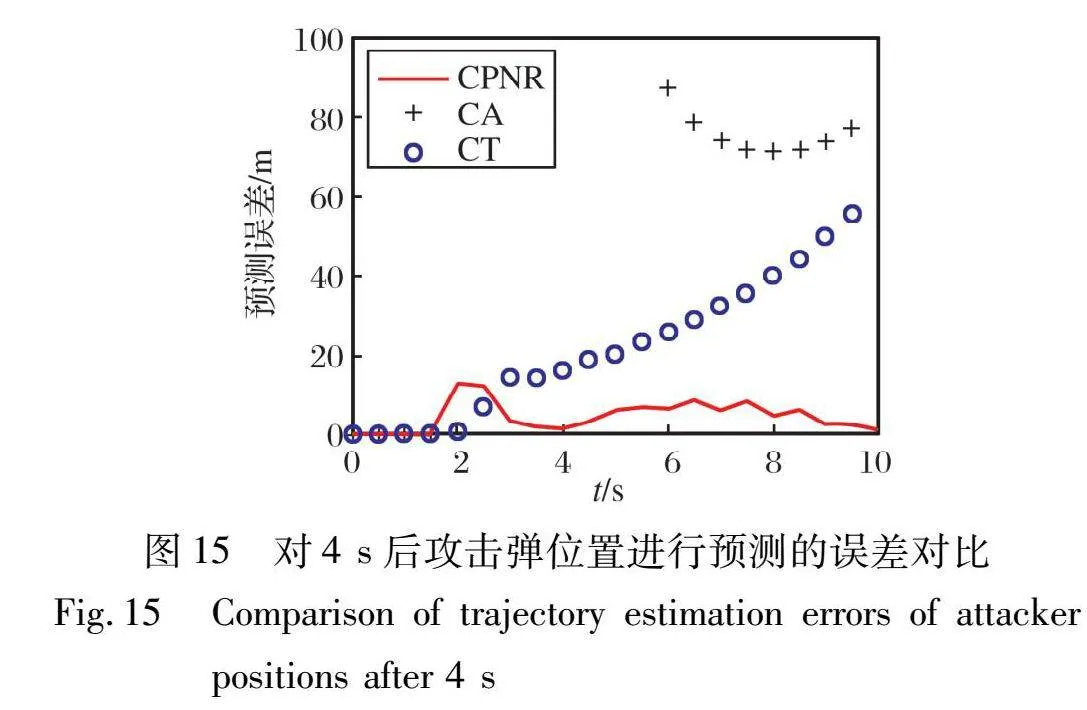
以每一時刻攻擊彈的狀態(tài)和未來幾秒內(nèi)載機的位置變化趨勢為依據(jù)進行外推， 得到一定預(yù)測時間后的預(yù)測誤差， 與CA和CT模型的預(yù)測結(jié)果進行對比， 得到不同預(yù)測時間下三種模型軌跡預(yù)測誤差的對比圖， 如圖13～15所示。

圖中， 縱坐標(biāo)代表當(dāng)前時間下對一定時長以后攻擊彈軌跡進行預(yù)測的位置結(jié)果與對應(yīng)時間后攻擊彈真實位置的偏差， 預(yù)測過程均從0 s開始到11 s結(jié)束。

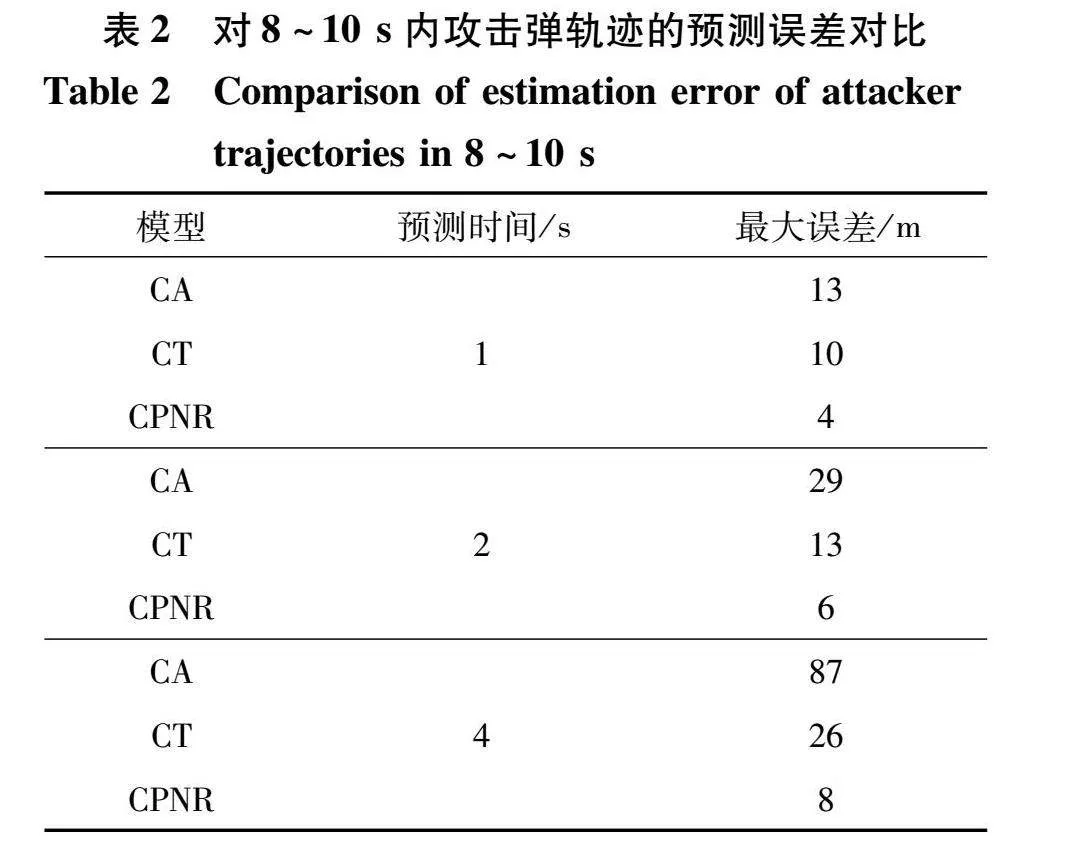
對比圖13～15可知， 在不同的預(yù)測時間長度下， CPNR模型的預(yù)測誤差均小于CT和CA模型。 將攔截時間假設(shè)為8～10 s之間， 分析對該時間段攻擊彈的軌跡進行預(yù)測時產(chǎn)生的誤差， 此時軌跡預(yù)測的誤差數(shù)據(jù)分別為圖13中7～9 s部分、 圖14中6～8 s部分、 圖15中4～6 s部分， 結(jié)果如表2所示。

由表2可知， 三種模型下對于短時間的軌跡預(yù)測都有較小的誤差， 但是隨著預(yù)測時間的增長， CA和CT模型的預(yù)測誤差增大幅度遠(yuǎn)大于CPNR。 根據(jù)3.2.1節(jié)的推導(dǎo)結(jié)果， 在距離攻擊彈到達預(yù)定碰撞點前4 s時間間隔的預(yù)測誤差結(jié)果應(yīng)小于30.7 m， 且預(yù)定碰撞點攻擊彈的位置估計誤差小于3 m， 才能保證防御方攔截彈在剩余時間內(nèi)能夠逐漸修正誤差影響， 以較小的脫靶量命中目標(biāo)。 在直接進行狀態(tài)外推的情況下， CPNR模型也可滿足攔截過程需要的條件。

4 結(jié) 論

本文對非線性的攻擊彈與載機的運動關(guān)系進行研究， 基于擴展卡爾曼濾波設(shè)計了一種狀態(tài)估計模型， 采用該狀態(tài)模型對攻擊彈攻擊載機的過程進行仿真預(yù)測， 在引入相關(guān)載機位置信息的情況下， 能夠很大程度上屏蔽掉觀測過程中引入的高斯分布隨機噪聲的影響， 從而較為精確地得到攻擊彈的運動狀態(tài)和運動規(guī)律， 相比于常用的CA和CT模型有更小的估計誤差， 可為軌跡預(yù)測的應(yīng)用提供誤差更小的狀態(tài)估計值， 同時， 在直接用狀態(tài)外推方法時預(yù)測效果也能滿足攔截過程的脫靶量要求。

參考文獻：

［1］ 張蓬蓬， 張俊寶， 郭正玉. 第六代戰(zhàn)斗機制空武器發(fā)展淺析［J］. 飛航導(dǎo)彈， 2021（12）： 140-145.

Zhang Pengpeng， Zhang Junbao， Guo Zhengyu. Analysis on the Development of the Sixth Generation Combat Mechanism Air Wea-pon［J］. Aerodynamic Missile Journal， 2021（12）： 140-145.（in Chinese）

［2］ 段鵬飛. 空空導(dǎo)彈小/微型化發(fā)展趨勢與啟示［J］. 航空兵器， 2021， 28（3）： 18-21.

Duan Pengfei. Development Trend of Air-to-Air Missile Micro Minia-turization［J］. Aero Weaponry， 2021， 28（3）： 18-21.（in Chinese）

［3］ 喬要賓， 吳震， 呂明遠(yuǎn). 空中平臺主動防御系統(tǒng)發(fā)展現(xiàn)狀及關(guān)鍵技術(shù)［J］. 航空兵器， 2023， 30（2）： 77-82.

Qiao Yaobin， Wu Zhen， Lü Mingyuan. Development Status and Key Technologies of Air Platform Active Defense System［J］. Aero Weaponry， 2023， 30（2）： 77-82.（in Chinese）

［4］ 介沖. AIM-120空空導(dǎo)彈發(fā)展綜述［J］. 飛航導(dǎo)彈， 2015（3）： 22-26.

Jie Chong. Summary of Development of AIM-120 Air-to-Air Missile［J］. Aerodynamic Missile Journal， 2015（3）： 22-26.（in Chinese）

［5］ Song T L， Shin S J， Cho H. Impact Angle Control for Planar Engagements［J］. IEEE Transactions on Aerospace and Electronic Systems， 1999，35（4）：1439–1444.

［6］ Padhi R， Kothari M. Model Predictive Static Programming： A Computationally Efficient Technique for Suboptimal Control Design［J］. International Journal of Innovative Computing Information & Control， 2009， 5（2）： 399-411.

［7］ 李轅， 趙繼廣， 白國玉， 等. 基于預(yù)測碰撞點的剩余飛行時間估計方法［J］. 北京航空航天大學(xué)學(xué)報， 2016， 42（8）： 1667-1674.

Li Yuan， Zhao Jiguang， Bai Guoyu， et al. Method of Time-to-Go Estimation Based on Predicted Crack Point［J］. Journal of Beijing University of Aeronautics and Astronautics， 2016， 42（8）： 1667-1674.（in Chinese）

［8］ 李庚澤， 魏喜慶， 王社陽. 基于軌跡預(yù)測的高超聲速飛行器攔截中/末制導(dǎo)研究［J］. 上海航天， 2017， 34（6）： 7-12.

Li Gengze， Wei Xiqing， Wang Sheyang. Study on Trajectory Predicting and Midcourse/Terminal Guidance Against Hypersonic Vehicle［J］. Aerospace Shanghai， 2017， 34（6）： 7-12.（in Chinese）

［9］ 周池軍， 李明杰， 雷虎民. 臨近空間再入滑翔目標(biāo)軌跡預(yù)測研究進展綜述［J］. 飛航導(dǎo)彈， 2021（6）： 127-132.

Zhou Chijun， Li Mingjie， Lei Humin. Review on the Research Progress of Near Space Reentry Gliding Target Trajectory Prediction［J］. Aerodynamic Missile Journal， 2021（6）： 127-132.（in Chinese）

［10］ 張浩， 張奕群， 張鵬飛. 三體對抗中的制導(dǎo)控制研究方法綜述［J］. 戰(zhàn)術(shù)導(dǎo)彈技術(shù)， 2021（1）： 67-73.

Zhang Hao， Zhang Yiqun， Zhang Pengfei. A Survey of Guidance Law Design in Active Target Defense Scenario［J］. Tactical Missile Technology， 2021（1）： 67-73.（in Chinese）

［11］ Chen X T， Wang J Z. Optimal Control Based Guidance Law to Control both Impact Time and Impact Angle［J］. Aerospace Scien-ce and Technology， 2019， 84： 454-463.

［12］ He S M， Lee C H， Shin H S， et al. Optimal Three-Dimensional Impact Time Guidance with Seeker’s Field-of-View Constraint［J］. Chinese Journal of Aeronautics， 2021， 34（2）： 240-251.

［13］ Li H Y， He S M， Wang J， et al. Near-Optimal Midcourse Gui-dance for Velocity Maximization with Constrained Arrival Angle［J］. Journal of Guidance， Control， and Dynamics， 2021， 44（1）： 172-180.

［14］ 劉滔， 雍恩米， 翟岱亮. 面向攔截的高超聲速飛行器軌跡預(yù)測關(guān)鍵技術(shù)綜述［J］. 航天控制， 2021， 39（4）： 13-21.

Liu Tao， Yong Enmi， Zhai Dailiang. A Review of the Key Technologies of Trajectory Prediction of Intercepting Hypersonic Vehicles［J］. Aerospace Control， 2021， 39（4）： 13-21.（in Chinese）

［15］ 徐世南， 吳催生. 高超聲速飛行器熱力環(huán)境數(shù)值仿真研究綜述［J］. 飛航導(dǎo)彈， 2019（7）： 26-30.

Xu Shinan， Wu Cuisheng. Summary of Numerical Simulation Research on Thermal Environment of Hypersonic Vehicle［J］. Aerodynamic Missile Journal， 2019（7）： 26-30.（in Chinese）

［16］ 桂業(yè)偉， 劉磊， 魏東. 長航時高超聲速飛行器的綜合熱效應(yīng)問題［J］. 空氣動力學(xué)學(xué)報， 2020， 38（4）： 641-650.

Gui Yewei， Liu Lei， Wei Dong. Combined Thermal Phenomena Issues of Long Endurance Hypersonic Vehicles［J］. Acta Aerodynamica Sinica， 2020， 38（4）： 641-650.（in Chinese）

［17］ 趙忠良， 吳軍強， 李浩， 等. 高機動導(dǎo)彈氣動/運動/控制耦合的風(fēng)洞虛擬飛行試驗技術(shù)［J］. 空氣動力學(xué)學(xué)報， 2016， 34（1）： 14-19.

Zhao Zhongliang， Wu Junqiang， Li Hao， et al. Wind Tunnel Based Virtual Flight Testing of Aerodyanmics， Flight Dynamics and Flight Control for High Maneuver Missle［J］. Acta Aerodynamica Sinica， 2016， 34（1）： 14-19.（in Chinese）

［18］ 解國棟， 黃今， 楊建昌， 等. 一種導(dǎo)彈飛行軌跡運動參數(shù)計算方法［C］ ∥第二屆中國指揮控制大會， 2014.

Xie Guodong， Huang Jin， Yang Jianchang， et al. A Calculation Approach for Kinematics Parameters of Missile Trajectory［C］ ∥The 2nd China Command and Control Conference， 2014.

［19］ 宗群， 李智禹， 葉林奇， 等. 變信賴域序列凸規(guī)劃RLV再入軌跡在線重構(gòu)［J］. 哈爾濱工業(yè)大學(xué)學(xué)報， 2020， 52（3）： 147-155.

Zong Qun， Li Zhiyu， Ye Linqi， et al. Variable Trust Region Sequential Convex Programming for RLV Online Reentry Trajectory Reconstruction［J］. Journal of Harbin Institute of Technology， 2020， 52（3）： 147-155.（in Chinese）

［20］ 史恒， 朱紀(jì)洪. 主動防御的最優(yōu)預(yù)測協(xié)同制導(dǎo)律研究［J］. 空間控制技術(shù)與應(yīng)用， 2019， 45（4）： 64-70.

Shi Heng， Zhu Jihong. Optimal Cooperative Prediction Guidance Law for Active Defense［J］. Aerospace Control and Application， 2019， 45（4）： 64-70.（in Chinese）

［21］ 謝麗， 張軍峰， 隋東， 等. 基于交互式多模型濾波算法的航跡預(yù)測［J］. 航空計算技術(shù)， 2012， 42（5）： 68-70.

Xie Li， Zhang Junfeng， Sui Dong， et al. Aircraft Trajectory Prediction Based on Interacting Multiple Model Filtering Algorithm［J］. Aeronautical Computing Technique， 2012， 42（5）： 68-70.（in Chinese）

［22］ 孫瑜， 吳楠， 孟凡坤， 等. 考慮J2攝動的彈道導(dǎo)彈高精度彈道預(yù)報和誤差傳播分析［J］. 彈道學(xué)報， 2016， 28（2）： 18-24.

Sun Yu， Wu Nan， Meng Fankun， et al. Analysis on High Precision Trajectory Prediction and Error Propagation of Ballistic Missile Considering J2 Perturbation［J］. Journal of Ballistics， 2016， 28（2）： 18-24.（in Chinese）

［23］ 袁震宇， 鐘志通， 張林， 等. 導(dǎo)彈末端彈道擬合方法研究［J］. 艦船電子工程， 2015， 35（11）： 52-54.

Yuan Zhenyu， Zhong Zhitong， Zhang Lin， et al. Missile Terminal Ballistic Curve Fitting Methods［J］. Ship Electronic Engineering， 2015， 35（11）： 52-54.（in Chinese）

［24］ 高策， 張淑梅， 趙立榮， 等. 基于數(shù)值積分法的彈道導(dǎo)彈落點實時預(yù)測［J］. 計算機測量與控制， 2012， 20（2）： 404-406.

Gao Ce， Zhang Shumei， Zhao Lirong， et al. A Real-Time Forecast Method for Impact Point of Ballistic Missile Based on Numerical Methods of Integration［J］. Computer Measurement & Control， 2012， 20（2）： 404-406.（in Chinese）

［25］ 楊彬， 賀正洪. 一種GRNN神經(jīng)網(wǎng)絡(luò)的高超聲速飛行器軌跡預(yù)測方法［J］. 計算機應(yīng)用與軟件， 2015， 32（7）： 239-243.

Yang Bin， He Zhenghong. Hypersonic Vehicle Track Prediction Based on GRNN［J］. Computer Applications and Software， 2015， 32（7）： 239-243.（in Chinese）

［26］ 宋波濤， 許廣亮. 基于LSTM與1DCNN的導(dǎo)彈軌跡預(yù)測方法［J］. 系統(tǒng)工程與電子技術(shù)， 2023， 45（2）： 504-512.

Song Botao， Xu Guangliang. Missile Trajectory Prediction Method Based on LSTM and 1DCNN［J］. Systems Engineering and Electronics， 2023， 45（2）： 504-512.（in Chinese）

［27］ Boyell R. Defending a Moving Target Against Missile or Torpedo Attack［J］. IEEE Transactions on Aerospace and Electronic Systems， 1976， AES-12（4）： 522-526.

［28］ 任淼， 劉晶晶， 劉凱， 等. 2022年國外空空導(dǎo)彈發(fā)展動態(tài)研究［J］. 航空兵器， 2023， 30（4）： 33-41.

Ren Miao， Liu Jingjing， Liu Kai， et al. Research on Foreign Air-to-Air Missiles’ Development in 2022［J］. Aero Weaponry， 2023， 30（4）： 33-41.（in Chinese）

Research on State Estimation Method Applied to Trajectory

Prediction of Air Platforms Active Defense Operations

Lü Mingyuan1， Wu Zhen1， 2*， Qiao Yaobin1， 2

（1. China Airborne Missile Academy， Luoyang 471009， China;

2. National Key Laboratory of Air-based Information Perception and Fusion， Luoyang 471009， China）

Abstract： Starting with the actual operational requirements of active defense， this paper analyzes the advantages， disadvantages， and usage scenarios of different trajectory prediction methods， also analyzes the differences between the active defense combat scenarios of air platforms and other aircraft trajectory prediction scenarios that are currently mainly studied. A state estimation scheme based on extended Kalman filtering is proposed for the special attack intent and motion law of the trajectory prediction object in this scenario. It simulates the process of the attack missile guided with proportional guidance law attacking aircraft based on simulation software， to establish an observation model under conditions of constant proportional guidance coefficient， and performs linearization simulation using Kalman filter nonlinear model. The motion states of the attack missile at different times are observed and the short-term trajectory prediction is performed. The simulation results show that the model can significantly reduce state estimation errors in the active defense combat scenario.

Key words： air to air missile; active defense； three-player conflict; trajectory prediction; state estimation; extended Kalman filter