“三教”改革背景下中職數學課程思政的“233”策略

在“三教”改革背景下，課程思政的實施是一個豐富而系統的過程，涵蓋教師、教材、教法三個維度。教師是課程思政實施主體，教材是課程思政實施載體，教法是課程思政實施策略。教師可通過重構教學內容，優化教學供給，創新教學方法，實現課程育人目標。

下面以中職數學為例，探討基于“三教”改革背景下課程思政的兩線三有三化策略（簡稱“233”策略）。

一、重構教學內容

教學內容的重構是一個持續的、動態的過程，需要基于學情與學科核心素養需求，不斷審視和改進，以學習知識為明線，課程思政為隱線（簡稱“兩線”），將顯性課程與隱性課程有機融合。

（一）學情為起點

學生的知識儲備、興趣、風格是學情的構成要素，教學內容的選擇既要以國家規劃教材為藍本，又要根據學情做策略性的重構，確保教學內容與學情契合。

例1數列的概念

教材：以2015-2019年國內生產總值及其增長速度統計圖創設情境引入數列的概念。

重構：以每個學生自己的章節測驗成績創設情境引入數列的概念。

比較：國內生產總值是一個重要的經濟指標，對于沒有學過政治經濟學的學生而言，過于宏觀與抽象。學生的章節測驗成績是一個重要的學習量化數據，能夠切身反映學習成效，具有代入感，學生可以觀察成績的變化趨勢反思學習方法，助力其形成學習過程自我監測與目標管理意識。

（二）素養為支點

例2等比數列的概念

教材：以古代數學著作《孫子算經》中“今有出門望見九堤，堤有九木，木有九枝，枝有九巢，巢有九禽，禽有九雛，雛有九毛，毛有九色。問：各幾何？”創設情境引入等比數列的概念1 。

重構：以《莊子·天下篇》中“一尺之錘，日取其半，萬世不竭”創設情境引入等比數列的概念。

比較：《孫子算經》中的堤、木、枝、巢、禽、雛、毛、色屬于理想化虛擬情境，缺乏現實色彩，難以共情。《莊子·天下篇》中“一尺之錘”蘊含了有限物質的無限可分性，是極限思想的生動詮釋，體現了莊子的哲學智慧，不僅是中華優秀傳統文化進行數學表達的絕佳素材，還是發展數學建模與邏輯推理兩大數學核心素養的支點。

二、優化教學供給

好的課堂，學生不僅能收獲知識的增長，能力的提高，還能獲得積極的情感體驗，形成正確的價值觀念。因此，教學設計要打破慣性，優化教學供給，確保課程思政有用、有趣、有效（簡稱“三有”），實現課程學習與價值引領相互融合，有機統一。

（一）有用為原則

課程思政要確保內容與學科知識具有關聯性，學生能夠從中獲得有價值的知識和思想，滿足學生的成長和發展需求。

例3艾賓浩斯曲線與函數單調性

教材：在函數的單調性這一節的內容中，將艾賓浩斯“遺忘曲線”以文字閱讀形式放在習題的“學以致用”部分。

優化：將將艾賓浩斯“遺忘曲線”前置，為函數單調性學習創設情境。

比較：優化前的“遺忘曲線”放在習題的最后，類似于拓展性閱讀，容易被學生忽略。將“遺忘曲線”前置，為單調性概念學習引入曲線模型，一方面將單調性概念可視化呈現，另一方面可以借助曲線特征分析，揭示學習需要通過及時復習降低遺忘速度，溫故知新。

（二）有趣為媒介

課程思政教學要采用生動有趣的素材和媒介，激發學生的學習興趣和參與熱情，使課程思政更加貼近學生的生活和心理。

例4莫比烏斯帶與和角公式

教材：和角公式包括兩角和與差的正弦公式、余弦公式及正切公式，教材呈現“公式推導-應用”的邏輯結構。

優化：莫比烏斯帶是一個具有單一面和單一邊界的非定向的二維表面，它可以通過取一條矩形紙帶，將一端翻轉180°后與另一端黏合而成。莫比烏斯帶的引入旨在鼓勵學生打破慣性，創新問題解決策略。

比較：教材直接給出公式應用例題，學生難以獲得切入點。和角公式的逆向使用，恰似莫比烏斯帶“180°旋轉”，形成整體思想，改變公式從左到右的應用慣性。借助莫比烏斯有趣媒介啟發學生：無論是行為習慣還是學習思維方式，都要小調整，大突破。

（三）有效為目標

課程思政教學要注重理論與實踐的結合，鼓勵學生將所學知識應用到實際生活中，通過實踐活動來加深理解和體驗，提高課程思政的實效性。

例5銀行存款與等比數列

教材：教材以“求報紙對折層數所構成的等比數列通項公式，并問第幾次對折后報紙層數是128？”作為典型例題。

優化：將報紙對折問題調整為學生存款問題，設計如下。

假設六年后，你立足社會有了存款能力，在銀行存了10萬元，以年利率2%計算，請寫出你存款后第1年、第2年、第3年、…、第n年的賬戶金額數據（不考慮利率變化）。試問：大約存款多少年后你的銀行賬戶可達20萬元？對此，你獲得什么啟示？（參考數據：10×1.0235≈19.99889552662455）

比較：“報紙對折”是一個簡易實驗，未必能觸動學生，而“銀行存款”問題是每個人會遇到的必修課，可助力學習者進行存款賬戶的趨勢分析。參考數據表明，要用超過35年的時間才能實現財富增值到原來的兩倍。借此給學生啟示：財富來之不易，要學會感恩，學會財富規劃。

三、創新教學方法

課程思政實施的探索與實踐，需要創新課程思政形式，探究情境創設、AI賦能、有機融入，使課程思政內容情境化、資源數字化、過程無痕化（簡稱“三化”），促進課程思政的學教方式變革。

（一）內容情境化

將抽象的思政理論融入學生的日常生活、學習環境、時政熱點等具體的情境中，有助于學生更好地理解理論與現實世界的聯系，引起學生的情感共鳴，避免“干巴巴的說教”，增強學科育人的針對性、吸引力和實效性。

例6數學運算與工匠精神

正確的數學運算是個人成長與經濟社會高質量發展的重要基礎，而數學運算錯誤在某些情況下責可能會導致嚴重的后果，尤其是在需要精確計算的領域，如航天、建筑、醫療等。

情境1：1970年，一個簡單的數學運算錯誤導致美國阿波羅13號登月任務失敗，造成巨大的損失。

情境2：大國工匠胡雙錢30年的航空技術制造中，基于正確的數學運算，零差錯完成數十萬精密零部件加工。

目標：借助數學運算正反面案例分析，幫助學生發展數學運算核心素養，形成正確數學運算的良好習慣與精益求精的工匠精神。

（二）資源數字化

例7函數奇偶性與文化自信

函數奇偶性是描述函數圖像關于原點或y軸對稱性的重要概念，故宮的建筑群以一條明顯的中軸線為對稱軸，兩邊的建筑嚴格對稱。函數奇偶性與故宮建筑群高度關聯。

情境：創建北京故宮建筑群的視頻資源，借助AI展示故宮建筑關于中軸線對稱的幾何特征。

目標：通過函數圖像的數學視角，分析中國建筑、雕塑、繪畫等的美學呈現，弘揚中國古建筑文化，增強家國情懷與文化自信。

（三）過程無痕化

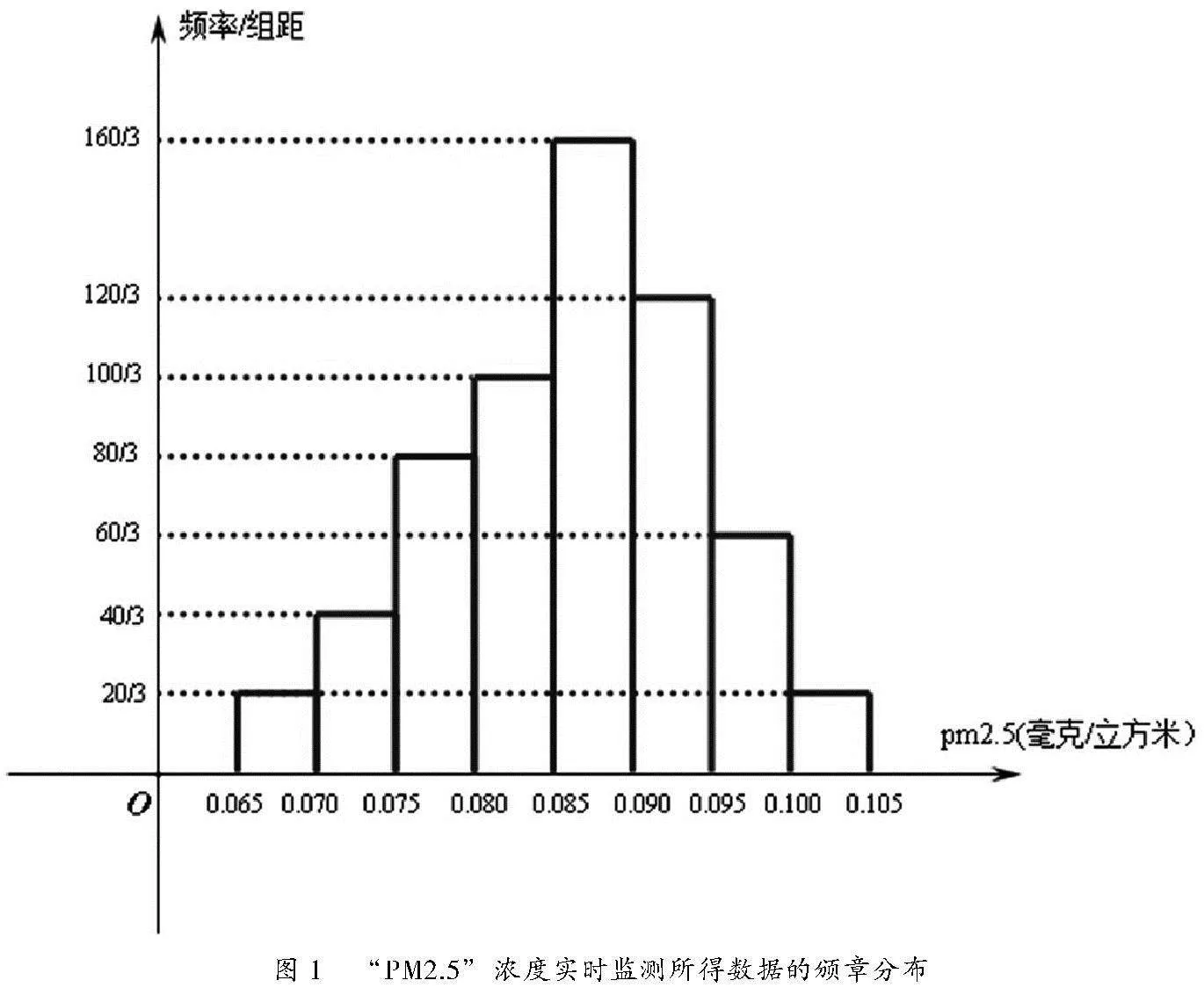
例8頻率分布直方圖與環保意識

頻率分布直方圖可直觀反應樣本數據的分布情況，以此推斷和估計總體中事件發生的概率。

情境：某年11月，某市自動監測站連續30天24小時對“PM2.5”濃度實時監測所得數據的頻率分布直方圖如圖1所示。根據國內標準，“PM2.5”24小時平均濃度值不超過0.075毫克/立方米時，空氣質量等級為良。求該市11月“PM2.5”空氣質量為良的天數。

目標：以試題考查方式，通過樣本數據分析該市11月份空氣質量為良的天數，引發學生對導致空氣污染源的探討，建立環保意識與低碳出行理念，實現課程思政無痕化地有機融入。