峰值提取結合變分模態分解的復雜樣品光譜去噪方法研究

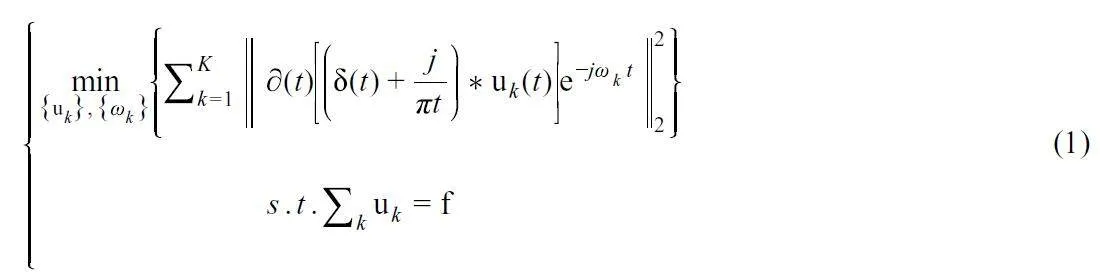
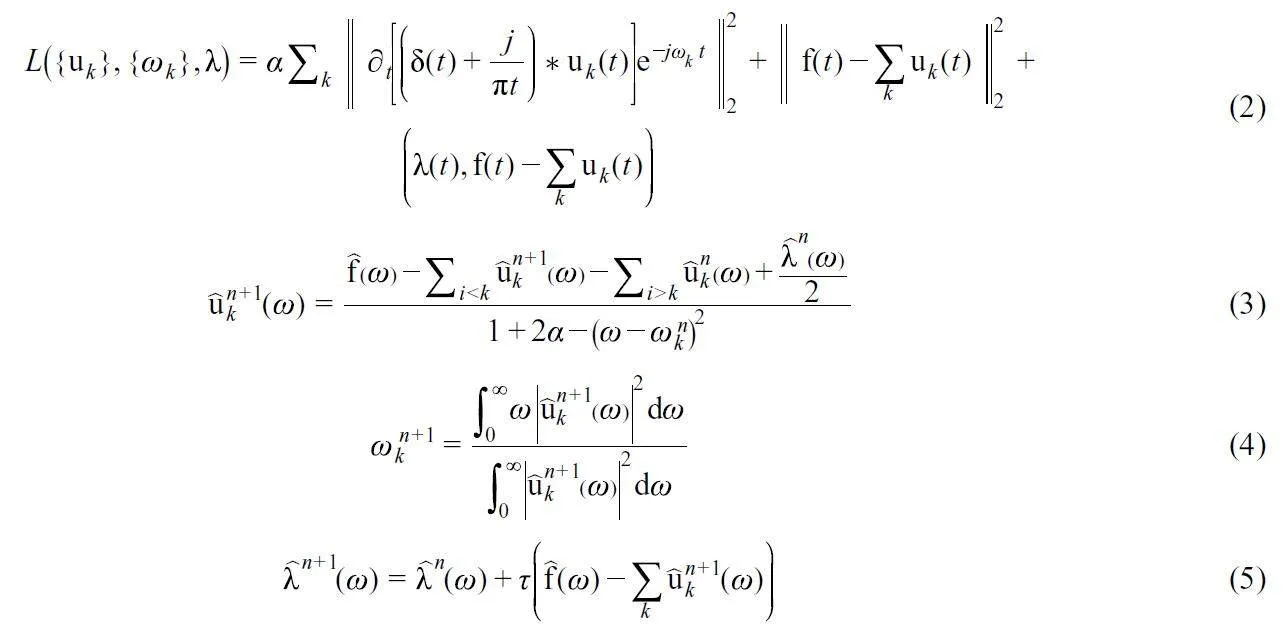
摘要 為解決變分模態分解（Variational mode decomposition， VMD）用于包含尖銳峰值的光譜去噪時產生的峰損失的問題，本研究提出了峰值提取結合變分模態分解（Peak extraction variational mode decomposition，PE-VMD）的復雜樣品光譜信號去噪方法。首先，采用VMD 對光譜信號進行去噪；然后，計算光譜信號的一階導數以確定峰值中心，計算光譜信號的二階導數以提取高信噪比的峰；最后，將VMD 去噪后丟失信息的峰截取去除，剩余光譜與提取的尖銳峰值依次連接，得到最終的去噪光譜。將本方法用于模擬信號和雙金屬催化劑（MnCo-ISAs/CN）的X-射線衍射（X-ray diffraction， XRD）譜去噪，并與Savitzky-Golay（SG）平滑、經驗模態分解（Empirical mode decomposition， EMD）和VMD 方法進行比較，采用去噪前后的光譜圖和信噪比評價去噪效果。結果表明， PE-VMD 去噪具有最大的信噪比，并且有效保留了光譜信號的有用信息。因此，對于包含尖銳峰值的光譜， PE-VMD 具有更優異的去噪能力。

關鍵詞 光譜去噪；變分模態分解；峰值提取；X射線衍射

在信號處理領域，變分模態分解（Variational mode decomposition， VMD）[1-2]作為一種新興的自適應信號分解技術，近年來受到了廣泛關注。與傳統的信號處理方法（如Savitzky-Golay（SG）平滑[3-4]和經驗模態分解（Empirical mode decomposition， EMD）[5]）相比， VMD 表現出一系列獨特的優勢：VMD 具有堅實的數學理論基礎，能夠確保分解結果的穩定性和準確性；VMD 在處理非線性和非平穩信號時表現出更高的自適應性，能夠更準確地提取出信號中的有用信息；VMD 可以改善EMD 在分解時產生的模態混疊和端點效應[6]。

鑒于VMD 在信號處理方面的顯著優勢，該技術已在軸承故障診斷[7]、管道泄漏檢測[8]和風速預測[9]等多個領域中得到廣泛應用，并且在去噪方面表現出色。近年來， VMD 在復雜樣品光譜去噪方面的應用潛力也逐漸受到關注。Guo 等[10]將VMD 應用于核磁共振（Nuclear magnetic resonance， NMR）譜的去噪，成功去除了光譜數據中的噪聲干擾，通過數值模擬和現場核磁共振測井數據處理，評估了VMD 方法對回波數據去噪的有效性和實用性。隨后，倪曉芳等[11]將VMD 應用于地下水重金屬檢測熒光光譜（Fluorescence spectroscopy， FS）的去噪，同樣取得了令人滿意的效果。本研究組[12]進一步探索了VMD 在拉曼光譜（Raman spectra）去噪中的應用，并與SG 平滑、小波變換（Wavelet transform， WT）和EMD 等傳統方法進行對比。結果表明， VMD 方法在去噪的同時能更有效地保留光譜信號中的有用信息。但是，當光譜信號包含尖銳峰時， VMD、SG 平滑、WT 和EMD 去噪都會產生一定程度的峰損失，其中， VMD 的峰值損失最小。Luo 等[13]提出了一種峰值提取結合移動平均平滑去噪的方法，該方法能夠有效去噪，并保留光譜中的高信噪比特征峰。

本研究結合峰值提取和VMD的優勢，提出了一種峰值提取結合變分模態分解（Peak extraction variationalmode decomposition， PE-VMD）的復雜樣品光譜信號去噪方法，用于解決尖銳峰值在VMD 去噪后出現的信息丟失的問題。通過對模擬信號和實測催化劑的X 射線衍射（X-ray diffractio

1 實驗部分

1.1 算法原理

1.1.1 變分模態分解

VMD 是一種自適應非遞歸信號的分解方法，其原理是將信號分解問題轉化為變分問題，通過連續迭代搜索得到問題的最優解。首先，對每個解析信號進行希爾伯特變換，得到單側頻譜；然后，將每個模態與其自身估計的指數中心頻率進行混合，使每個模態的頻率遷移到基帶[1]；最后，通過梯度的平方范數評估每個模態的帶寬[1]。因此，在所有模態之和等于原始信號的前提下，可以得到約束變分函數，如式（1）所示：

其中， {uk}和{ωk}分別表示分解得到的一系列模態的集合及其對應的中心頻率；δ（t）是一個沖擊函數；*表示卷積；f 表示原始信號。

通過引入二次懲罰項和拉格朗日乘子將上述問題轉化為無約束問題[8]，如式（2）所示。通過在傅里葉域中的迭代優化，并利用交替方向乘子法（Alternate direction method of multipliers， ADMM）[1]計算增廣拉格朗日函數的鞍點，其迭代公式由式（3）、式（4）和式（5）表示。

其中， f（ω ）、ui（ω ）、 λ（ ω）和uk （ω ）n+1 分別表示 f（ ω）、u （ω ） i 、 λ（ω ） 和 uk （ω ）n+1 的傅里葉變換。最后，對分析信號進行反傅里葉變換，得到最終模態。

原始信號經過VMD 可分解為K 個從高頻到低頻的模態uk，由于VMD 克服了EMD 的模態混疊效應，即VMD 分解后不同模態組分的頻率差異明顯。因此，采用VMD 對光譜信號進行去噪時，將高頻模態去除，低頻模態加和重構，即可得到去噪后的信號。

1.1.2 峰值提取結合變分模態分解的光譜去噪方法

盡管VMD 分解相較于SG 平滑、WT 和EMD 等可以獲得較好的去噪效果[12]，但當光譜信號中含有尖銳峰時， VMD 分解也會造成一定的信號損失。尖銳峰通常具有較高的信噪比，如果樣品是純物質，并且高信噪比的尖銳峰恰好對應目標分析物，則可直接使用該峰進行定性或定量分析。但是，復雜樣品通常是含有多種組分的混合物，譜峰重疊現象普遍，需要利用所有波長點的光譜數據與目標組分建立多元模型[8]，因此有必要對含高信噪比尖銳峰的光譜信號進行去噪。本研究提出了復雜樣品光譜去噪方法PE-VMD，一方面，通過VMD 將原始光譜信號分解為多個模態，然后根據各模態的頻率特性將高頻噪聲模態去除，保留低頻模態進行重構；另一方面，通過計算光譜的一階和二階導數尋找峰值的位置，并確定需要保留的高信噪比的峰及其寬度，在有效去除噪聲的同時避免了峰值損失。具體過程如下：（1） 通過VMD 將原始光譜信號分解為一系列的模態（uk）；（2） 將高頻模態作為噪聲去除，剩余的低頻模態進行重構，重構后的光譜信號在尖銳峰值處產生信息丟失現象；（3） 利用一階導數確定峰中心和峰寬，其中，一階導數從正變為負的零點對應于峰中心，而相鄰的局部最小點之間的距離定義為峰寬；（4） 計算光譜信號的二階導數，將二階導數作為高通濾波器，在放大噪聲的同時降低峰的信號強度，只有高信噪比的峰值才能持續保持二階導數小于0 的狀態，考慮到峰值的鄰域性，通過設定3～9 個點確定信噪比水平，并提取出靠近峰值中心的高信噪比點；（5） 從重構光譜中剔除產生信息丟失的峰值，將光譜剩余部分與提取的尖銳峰值部分依次連接。

1.1.3 SG 平滑

SG 平滑又稱卷積平滑，是一種基于時域局部多項式最小二乘擬合的平滑方法[14]。SG 平滑需要選取一定寬度且含有奇數個波長點的平滑窗口，采用對選取窗口內所有波長點進行多項式最小二乘擬合得到的值代替窗口內的中心波長點。SG 平滑的實質是一種加權平均方法[15]，更強調中心點的作用，使用i=2w+1 的對稱窗口，其中， i 和w 分別是移動窗口的點（即窗口大小）和半窗口寬度。SG 平滑在波長k 處的平滑值如式（6）所示：

其中， hi 是平滑系數，可通過基于最小二乘的多項式擬合得到；H 是歸一化因子。SG 平滑去除光譜噪聲的實質是通過最小二乘多項式擬合到連續的數據點窗中，以遵循光譜的形狀，進而降低隨機變化的噪聲信號的影響，已廣泛應用于化學、食品科學和生物醫學信號處理等多個領域的噪聲去除[16-19]。

1.1.4 經驗模態分解

EMD 是一種自適應的信號分解方法。通過篩分（Sifting）過程， EMD 能將光譜分解為一定數量的本征模態函數（Intrinsic mode functions， IMFs）分量和殘差（Residual， r）分量[20]。其中，每個IMF 都是1 個振蕩，并且隨著IMF 階數增加，振蕩程度逐漸降低。EMD 篩分過程如下。（1）求出原始光譜x 的所有極大值點和極小值點，并采用3 次樣條插值分別擬合形成極大值點包絡線和極小值點包絡線。（2）計算極大值點包絡線和極小值點包絡線的平均值m。（3）用原始信號x 減去均值m，即可得到光譜的局部細節信息h。（4）根據IMF 的兩個約束條件判斷h 是否為IMF：（a）在整個數據范圍內，極值點與過零點的個數必須相等或最多相差1；（b）在任何局部點上， 極大值和極小值的包絡平均值必須等于零， 若滿足， 則h 為分解得到的1 個IMF， 此時，殘差r=x?h；若不滿足，則將h 作為1 個新的原始信號x 重復上述步驟，直到r 滿足停止準則r=x?h。（5）原始信號x 經EMD 分解后得到n 個IMFs 和1 個r。

1.2 實驗數據

為了檢驗PE-VMD 方法的去噪效果，利用1 個模擬信號和MnCo-ISAs/CN 催化劑的XRD 譜進行驗證。

模擬信號由2 個不同峰寬和峰高的高斯函數、1 個背景函數和20 dB 的高斯白噪聲構成。為了進一步提高第二個尖銳峰的信噪比，將該峰附近9 個點的噪聲歸零，從而得到1 個含有高信噪比的尖銳峰的模擬信號，如圖1A 所示。2 個高斯函數y1、y2 以及背景函數y3 分別如式（7）、式（8）和式（9）所示，其中x 代表信號的位置，函數的形狀繪制在圖1B 中。該模擬信號由間隔為0.1 的551 個變量組成。由圖1A可以明顯觀察到，位于280 樣本點處的峰值幾乎不包含噪聲。

y = 0.03x／3 2 （9）

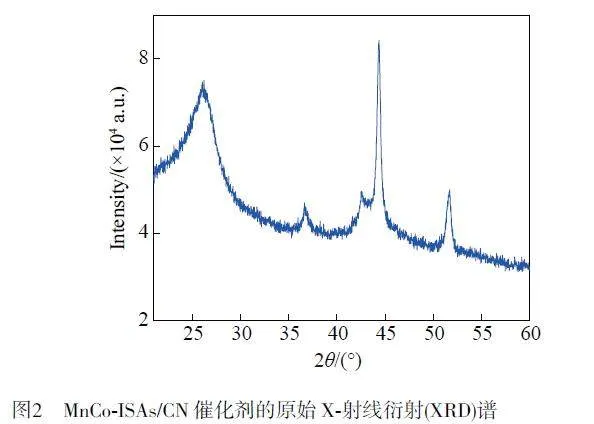
采用X-射線衍射儀（D/MAX-RB，日本理學電機公司）測量雙金屬催化劑材料（MnCo-ISAs/CN），得到XRD 譜（圖2），其衍射角范圍為20°～60°，間隔設置為0.02°，共1978 個變量。

2 結果與討論

2.1 光譜的變分模態分解

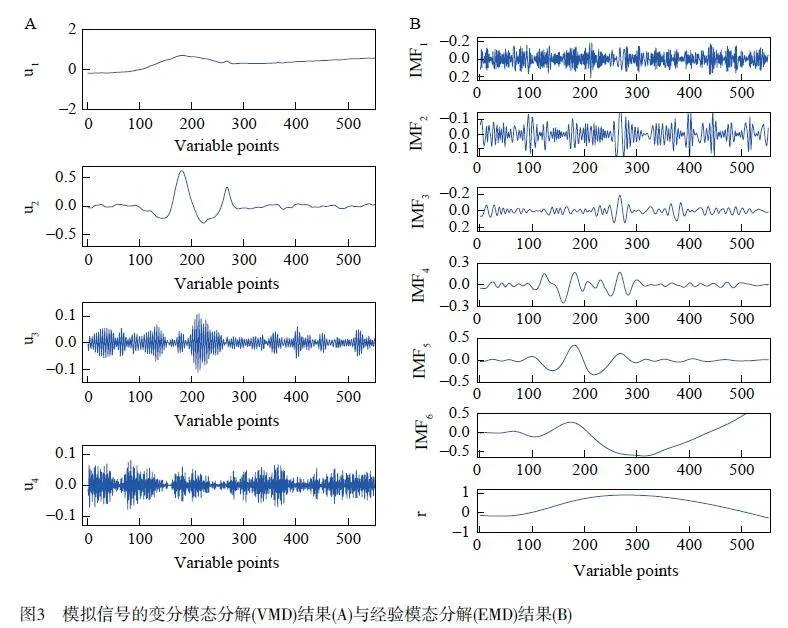
采用VMD 分解模擬信號，并對分解的結果進行分析。圖3A 表示模擬信號經過VMD 分解后的結果，共得到4 個模態u1～u4，振蕩頻率隨著階數增大而升高。對于大部分含噪光譜，噪聲主要累計在高頻成分中，有用信息主要累積在低頻成分中。通過觀察， u1 和u2 是振蕩速度極慢的低頻成分，而u3 和u4 含有大量尖銳峰值，是明顯的噪聲成分，幾乎不含有用信息。由此可見，信號在經VMD 分解后，能夠實現高頻與低頻成分的有效分離。

EMD 作為比較方法，對模擬信號的分解結果見圖3B，信號被分解為6 個IMF 模態和1 個殘差，即IMF1～IMF6 和r。與VMD 相反， EMD 的分解結果中模態的振蕩頻率隨著IMF 階數增大而降低。由分解的模態頻率可知， IMF1 和IMF2 分量的頻率較高，是非常明顯的噪聲。IMF3 分量在248～290 變量范圍內出現了幅度較小的頻率變化，其它變量范圍的頻率變化較大，出現了嚴重的模態混疊效應。IMF4～IMF6和r 都含有緩慢變化的峰，通過觀察可知其均為有用信息分量。

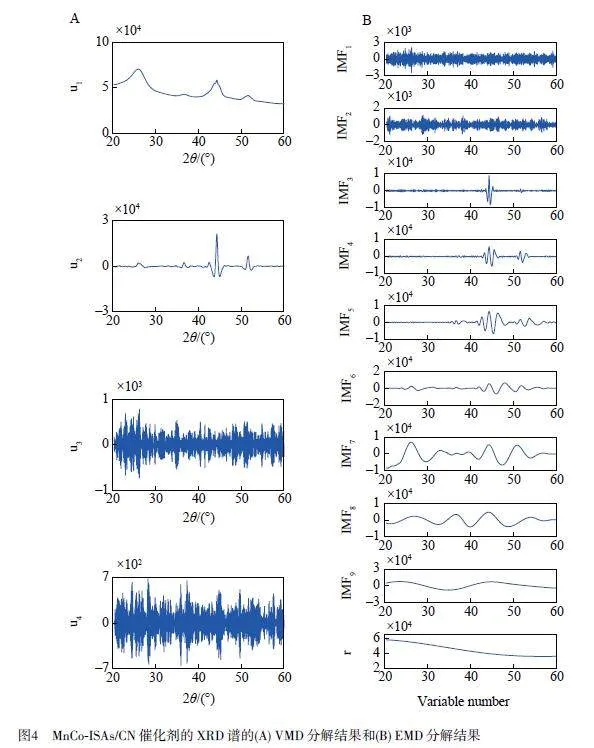
同樣，對MnCo-ISAs/CN 催化劑的XRD 譜進行VMD 分解和EMD 分解，結果見圖4。MnCo-ISAs/CN催化劑的XRD 譜經VMD 分解，共得到4 個模態u1～u4，并且振蕩頻率由上至下依次增大。通過觀察很容易區分噪聲模態和有用信息模態的邊界， u1 和u2 是低頻模態，而u3 和u4 是高頻模態。采用EMD 將MnCo-ISAs/CN 催化劑的XRD 譜分解為9 個IMFs（IMF1～IMF9）和1 個r，如圖4B 所示。與模擬信號的分解結果相似，隨著IMFs 階數增加，頻率逐漸降低。其中， IMF1 和IMF2 分量含有大量無序的尖銳峰值，為明顯的噪聲成分；IMF6～IMF9 上下波動很小，明顯含有大量有用信息；在IMF3、IMF4 和IMF5 3 個低頻模態中還包含許多高頻成分，出現了嚴重的模態混疊。

2.2 峰值提取

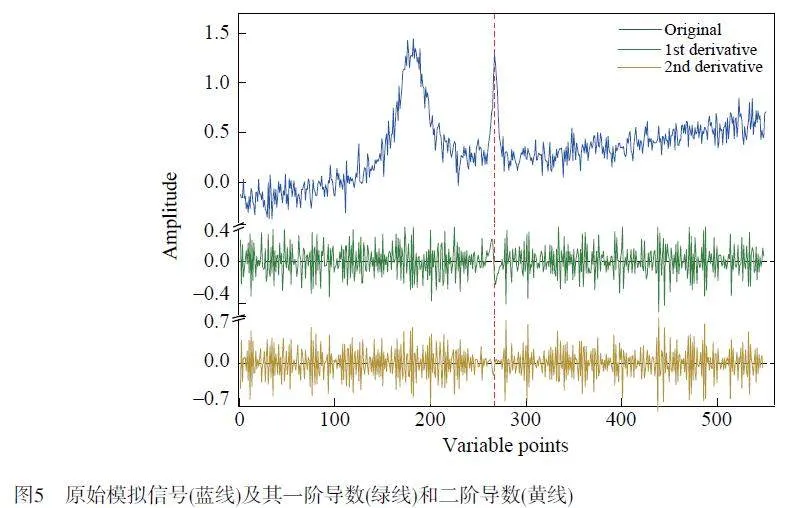
分別對模擬信號和MnCo-ISAs/CN 催化劑的XRD 譜進行高信噪比峰值的提取。圖5 表示模擬信號（藍線）和模擬信號的一階導數（綠線）和二階導數（黃色）曲線。首先，通過計算一階導數尋找峰值中心的位置，在一階導數的曲線中，位于267 數據點處的“零點”代表峰值中心。然后，計算二階導數，峰值中心相鄰的4 個點能夠在二階導數曲線中保持小于0，說明該峰值是高信噪比的峰值；在180 數據點處的峰值，其相鄰的點在二階導數曲線中并不能連續小于0，所以信噪比較弱。最后，對“零點”處的峰值進行提取。

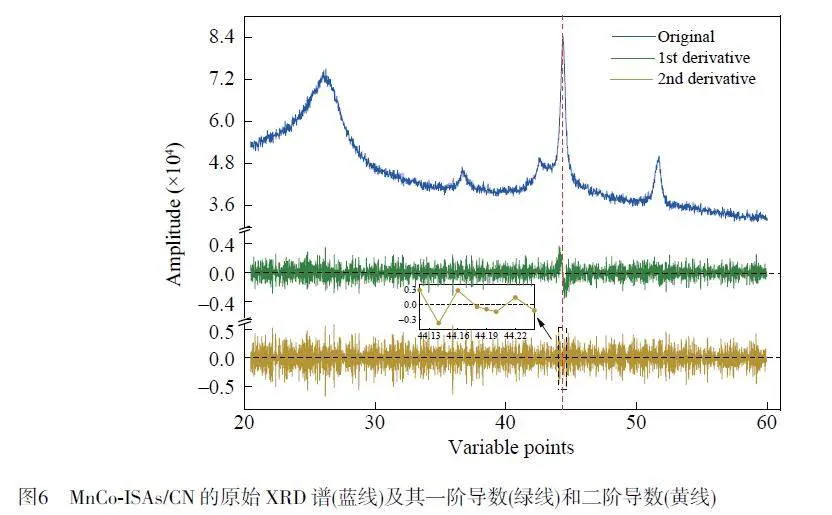
MnCo-ISAs/CN 催化劑的XRD 譜（藍線）及其一階導數（綠線）和二階導數（黃線）曲線如圖6 所示。首先，計算XRD 譜的一階導數以尋找峰值中心，可明顯觀察到在44.2°處一階導數由正數變為負數。其次，計算XRD 譜的二階導數，由于無法直接從圖6 中看出峰值中心處相鄰處有多少個點能夠在二階導數曲線中保持小于0，故添加了二階導數在44.2°處的峰值處的細節圖，從中可見峰值中心處相鄰的3 個點能夠在二階導數曲線中保持小于0，說明此峰具有較高的信噪比。因此，將峰值中心對應范圍內的峰值進行提取。

2.3 去噪結果比較

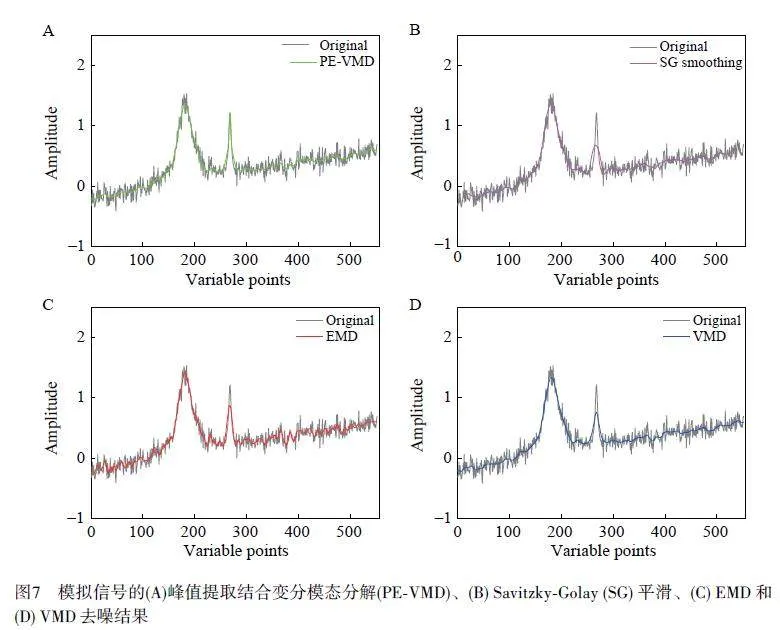
提取到高信噪比的尖銳峰后，將VMD 去噪后光譜中丟失信息的峰值截取去除，提取的峰與剩余光譜依次連接獲得最終的去噪光譜。PE-VMD 去噪后的模擬信號光譜見圖7A，其去噪效果尤為顯著。在180數據點處的峰， PE-VMD 去噪后的光譜不僅保持了高度的平滑性，而且有效保留了尖銳峰值的信息。進一步評估了PE-VMD 的去噪性能，將其與SG 平滑、EMD 和VMD 的去噪結果進行對比。圖7B～7D 分別展示了SG 平滑、EMD 和VMD 方法處理后的光譜。其中， SG 平滑的窗口選擇為33。EMD 分解后，高頻部分與低頻部分的邊界可確定為IMF2 和IMF3，但由于IMF3 中含有高頻和低頻兩種成分，故借助基于經驗模態分解及t 檢驗的噪聲去除方法[20]確定其用于重構去噪信號的去噪效果較佳。由圖7 可見， EMD去噪后出現不平整的現象并形成2 個小峰，而SG 平滑損失了更多信息。VMD 雖然在一定程度上保留了光譜信息，但在平滑度和信息保留方面仍不及PE-VMD。此外，分別計算了這4 種方法去噪后的信噪比，結果表明， PE-VMD 的信噪比為13.92，高于SG 平滑（12.66）、EMD（13.89）和VMD（13.44）。綜上所述，PE-VMD 在去噪前后的光譜圖和信噪比上都表現出了顯著優勢，不僅有效去除了噪聲，還保留了尖銳峰值的信息。與其它3 種方法相比， PE-VMD 的去噪性能更優。

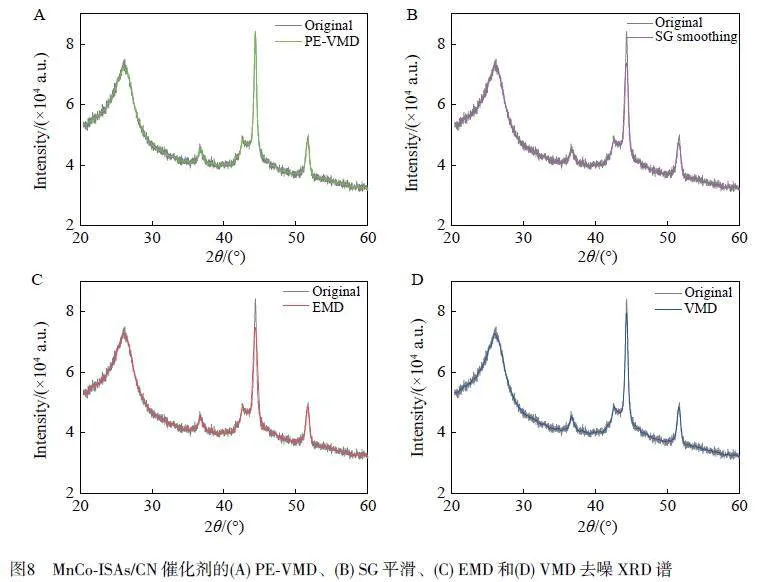
圖8A 展示了MnCo-ISAs/CN 催化劑的XRD 譜采用PE-VMD 方法去噪的結果，可見PE-VMD 不僅較大幅度提升了光譜的平滑度，而且有效保留了高信噪比下的尖銳峰值及關鍵信息。這是由于PE-VMD對VMD 方法的繼承與改進成功避免了EMD 可能引發的模態混疊問題，確保了去噪過程的高效與準確。為了更全面地評估PE-VMD 的性能，將其與SG 平滑、EMD 和VMD 對XRD 譜的去噪結果進行對比。圖8B～8D 分別為SG 平滑、EMD 和VMD 去噪后的XRD 譜。在SG 平滑處理中，窗口寬度為55。對于EMD 的分解結果，采用t 檢驗方法進行分析，發現當使用混疊模態IMF3 進行信號重構時，去噪效果更佳。由圖8 可見，位于27°～28°處的峰在SG 平滑和VMD 去噪后基本重合，但EMD 的結果不平滑，并出現了2 個峰；位于37°的峰在SG 平滑去噪后出現了過度平滑的現象；在45°的尖銳峰值處， SG 平滑、EMD和VMD 去噪后均丟失了部分有效信息。計算結果表明， SG 平滑、EMD 和VMD 的信噪比分別為13.96、14.7 和16.68，而PE-VMD 的信噪比為17.48，高于其它3 種方法。由上述結果可見，采用PE-VMD對MnCo-ISAs/CN 催化劑的XRD 譜進行去噪處理時，不僅提供了更平滑的光譜，還確保了關鍵峰值和信息的完整性，其效果明顯優于SG 平滑、EMD 和VMD 等方法。

3 結論

針對包含尖銳峰值的光譜，本研究提出了一種PE-VMD 復雜樣品光譜信號去噪的方法。采用VMD將光譜分解為一系列的模態（uk），確定用于重構信號的模態，得到重構后的光譜信號；計算光譜信號的一階導數，尋找尖銳峰值對應的“零點”，確定峰值中心位置；計算光譜信號的二階導數，提取并保留尖銳峰值；將VMD 去噪后丟失信息的峰截取去除，剩余光譜與提取的尖銳峰值依次連接，得到最終的去噪光譜。采用模擬信號以及MnCo-ISAs/CN 催化劑的XRD 譜分別驗證了本方法的可行性和效果。結果表明，與SG、EMD 和VMD 等方法相比， PE-VMD 在去除噪聲的同時有效保留了光譜的峰值信息，具有更好的去噪效果。

References

[1] DRAGOMIRETSKIY K， ZOSSO D. IEEE Trans. Signal Process. ， 2014， 62（3）： 531-544.

[2] SHEN S， WANG B， ZENG L， CHEN S， XIE L， SHE Z， HUANG L. Appl. Sci. ， 2024， 14（6）： 2243.

[3] SAVITZKY A， GOLAY M J E. Anal. Chem. ， 1964， 36（8）： 1627-1639.

[4] LEE J， LEE W. J. Raman Spectrosc. ， 2024， 55（4）： 525-533.

[5] HUANG N E， SHEN Z， LONG S R， WU M L C， SHIH H H， ZHENG Q N， YEN N C， TUNG C C， LIU H H. Proc. R. Soc. A，1998， 454（1971）： 903-995.

[6] YANG H， CHENG Y， LI G. Alexandria Eng. J. ， 2021， 60（3）： 3379-3400.

[7] LIU H， XU Q， HAN X， WANG B， YI X. Knowledge-Based Syst. ， 2024， 289： 111479.

[8] XU T， ZENG Z， HUANG X， LI J， FENG H. Process Saf. Environ. Prot. ， 2021， 153： 167-177.

[9] MORENO S R， SEMAN L O， STEFENON S F， COELHO L S， MARIANI V C. Energy， 2024， 292： 130493.

[10] GUO J F， XIE R H， WANG Y X， XIAO L Z， FU J W， JIN G W， LUO S H. IEEE Trans. Geosci. Electron. ， 2023， 61：5902014.

[11] NI Xiao-Fang， YANG Gui-Lan， TANG Xiao-Yong. Chin. J. Inorg. Anal. Chem. ， 2024， 14（5）： 677-684.

倪曉芳， 楊桂蘭， 唐曉勇. 中國無機分析化學， 2024， 14（5）： 677-684.

[12] BIAN X， SHI Z， SHAO Y， CHU Y， TAN X. Molecules， 2023， 28（17）： 6406.

[13] LUO S， WANG X， CHEN G， XIE Y， ZHANG W， ZHOU Z， ZHANG Z， REN B， LIU G， TIAN Z. Anal. Chem. ， 2021， 93（24）：8408-8413.

[14] CHEN D， CAI W， SHAO X. Anal. Bioanal. Chem. ， 2007， 387（3）： 1041-1048.

[15] HAIDER N S， PERIYASAMY R， JOSHI D， SINGH B K. Braz. Arch. Biol. Technol. ， 2018， 61： e18180203.

[16] RIVOLO S， PATTERSON T， ASRRESS K N， MARBER M， REDWOOD S， SMITH N P， LEE J. IEEE Trans. Biomed. Eng. ，2017， 64（5）： 1187-1196.

[17] XIA Z， YANG J， WANG J， WANG S， LIU Y. Appl. Spectrosc. ， 2020， 74（4）： 417-426.

[18] ACHARYA D， RANI A， AGARWAL S， SINGH V. Perspect. Sci. ， 2016， 8： 677-679.

[19] BIAN X， LING M， CHU Y， LIU P， TAN X. Front. Chem. ， 2022， 10： 949461.

[20] LING Meng-Xuan， LU Su-Min， SUN Hao， LIU Dan， BIAN Xi-Hui. Chin. J. Anal. Chem. ， 2023， 51（3）： 445-453.

凌夢旋， 盧素敏， 孫浩， 劉丹， 卞希慧. 分析化學， 2023， 51（3）： 445-453.

藥物制劑技術研究與評價國家藥品監督管理局重點實驗室開放課題項目（Nos. 2022TREDP04， 2023TREDP01）資助。