選編“好的問題”，踐行“三學”課堂

“自學·議論·引導”教學法倡導“三學”（即學材再建構、學法三結合、學程重生成），在新授課中，特別是單元教學中實踐較多。近一段時間以來，筆者用較多的時間和精力在九年級開展課堂教學與研究，對九年級復習課有較多的實踐和思考。本文以九年級“與圓有關的位置關系”復習課為例，談談如何選編“好的問題”，踐行“三學”課堂。

一、“與圓有關的位置關系”復習課教學設計

活動1：過一點作圓的切線

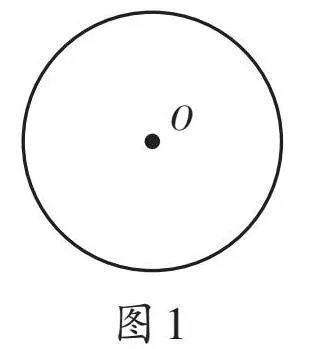
問題1：已知⊙O，如圖1，過一點P，畫出⊙O的切線。

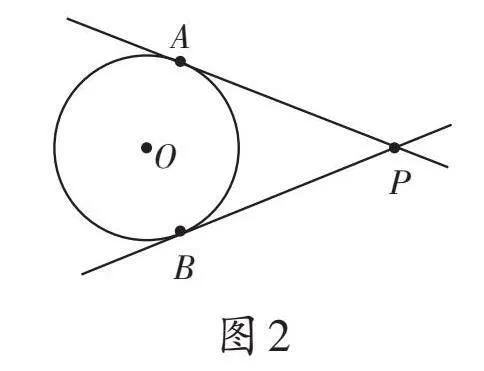
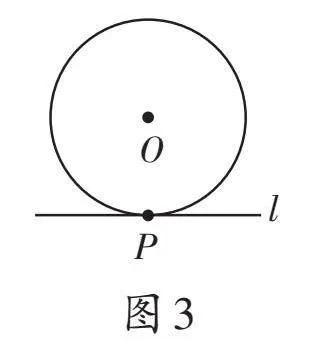
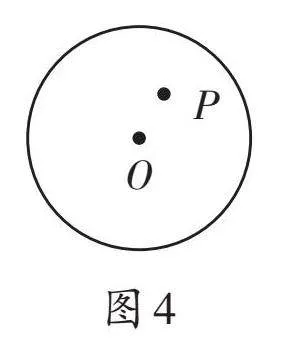
教學預設：這是一道“結構不良問題”。當學生發現在所給的圖1中沒有點P時，教師可及時引導：“同學們，你們可在圖1中添出一個點P，繼續求解。”這時學生就會想到需要分類討論（如圖2—4）。在三種點和圓的位置關系出示之后，教師可順便安排學生復習點到圓心的距離d與半徑r的大小關系（為節約用時，教師可以提前準備PPT以配合學生講解）。在圖2中，點P在⊙O外，過點P可以畫出兩條切線；圖3中，點P在⊙O上，過點P可以畫出一條切線；圖4中，點P在⊙O內，過點P不能畫出切線。特別是，結合圖4，學生會說出過圓內一點P不能畫出圓的切線，教師可追問：“能否畫圖演示，為什么不能畫出圓的切線？”學生可能會過點P畫出圓的割線，看出此時畫的線與圓有兩個公共點，不符合圓的切線定義，順勢也就復習了圓的切線、直線和圓的位置關系的相關知識。教師可結合PPT呈現相關知識結構圖（或思維導圖）。

需要說明的是，《義務教育數學課程標準（2022年版）》將尺規作圖“過圓外一點作圓的切線”作為選學內容，所以我們先安排的是“畫切線”活動，然后結合學情，相機安排學生“用尺規作圖，過圓上一點或圓外一點作圓的切線”。教師還可預設不同的作法，如文獻[2]中的教學實踐，作為教學引導時的“備用”。

活動2：切線長定理及基本圖形的研究

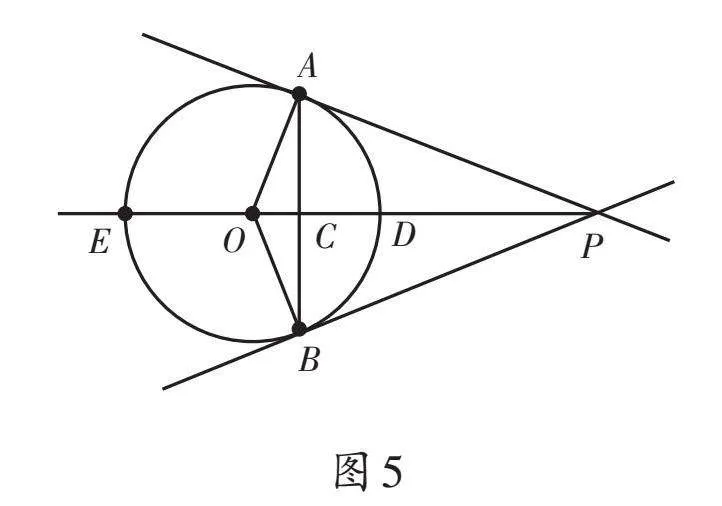
問題2：如圖5，PA、PB是⊙O的切線，切點分別是點A、B，射線PO交⊙O于點D、E，交弦AB于點C，你能找到哪些相等的線段和哪些相等的角？

教學預設：教師組織學生復習切線長定理時，可安排學生分組交流后，再在班級內進行匯報展示。如果學生講解圖5中相等的線段或角比較“雜亂、無序”，教師可追問其他學生“能否更加有序地說說，以便不重不漏”。教師在點評時，要注意從軸對稱（對稱軸是直線PO）和全等三角形的角度進行小結。順便指出，若是中考復習課，教師還可從相似的角度追問：“圖中有相似三角形嗎？舉例說說。”

活動3：三角形的內切圓和外接圓

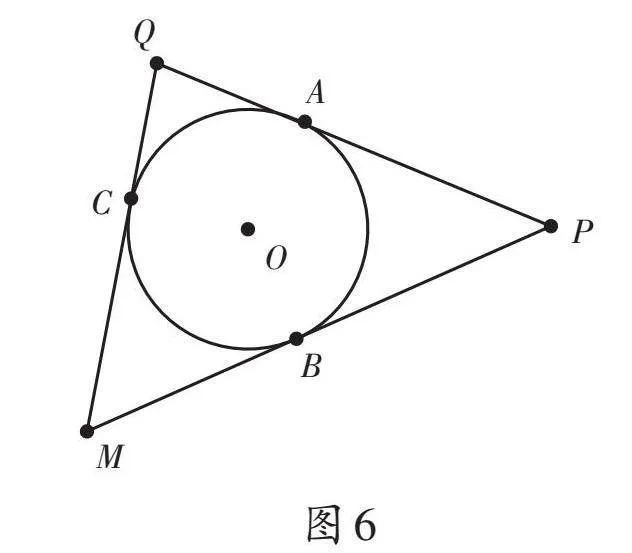
問題3：（在圖2的基礎上）如圖6所示，在⊙O上取一點C，過點C作⊙O的切線，并與⊙O的切線PA、PB相交于點Q、M。結合圖6，你想到了哪些數學概念？

教學預設：這是三角形內切圓的基本圖形，學生能聯想到三角形內切圓、內心等數學概念。這時教師可根據學情，繼續安排以下幾個小問題，幫助學生復習三角形內切圓的相關知識或性質。

（1）任意畫一個△ABC，如何用尺規作圖作出它的內切圓？（學生在小組內交流構圖思路和作法，然后教師安排學生口頭匯報作法步驟即可。教師也可以根據教情、學情，相機安排學生在黑板上進行作圖演示。）

（2）如圖6，若△PQM的周長為12，內切圓的半徑r=1，求△PQM的面積。

（3）若圖6中，QM=9，PQ=13，PM=14，求PA、QC、MB的長。

以上幾個問題都是新授課期間教材上曾出現的例題、習題，復習時應該不會耗時太多。如果學情較好，“問題3”的以上設問也不必全部呈現，以“開放式問題”代之，比如“請同學們結合圖6，設計一個問題并交流，有興趣的同學可以在課后深入研究”。

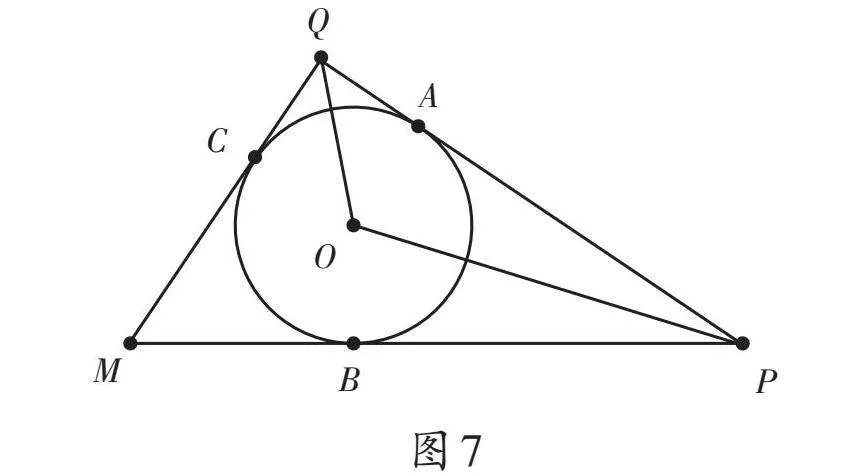
問題4：如圖7，在Rt△MPQ中，∠PQM=90°，⊙O是△MPQ的內切圓，切點分別為點A、B、C。

（1）當∠MPQ=40°時，求∠POQ的度數。

（2）若AP=6，MC=4，請設計一個問題，先在小組內交流，再在班級內展示設計意圖與求解思路。

教學預設：第（1）問可直接根據三角形內角和、角平分線性質求解；第（2）問比較開放，教師要充分預設學生可能的設問，如求Rt△MPQ各邊長、圖7中所有線段的長、內切圓⊙O的半徑、三角形PQM的周長與面積，等等。在學生交流展示各組的設計問題之后，教師給出以下追問，將問題進一步變式拓展。

追問1：上面已經復習了三角形的內切圓及作法，同學們想一想，怎樣作出一個三角形的外接圓呢？圖7中，有比較快的方法作出直角三角形MPQ的外接圓嗎？

教學預設：通過“追問1”，順勢復習三角形的外接圓、外心等數學概念。學生熟悉相關作法，而圖7中的△PQM是直角三角形，作出其外接圓的較快的方法是先確定外心（斜邊PM的中點），這樣就可以很容易地作出△PQM的外接圓了。

追問2：在上面第（2）問的條件下，設O′是△MPQ的外心，求OO′的長。

教學預設：“追問2”的本質是分析“三邊分別為6、8、10的直角三角形的內心與外心之間的距離”。

活動4：課堂小結

小結問題1：今天我們復習了點和圓、直線和圓、三角形和圓的位置關系，我們是如何來研究的？哪些問題給你留下了較深的印象？

預設：本節課我們是從“過一點，畫圓的切線”開始，依次復習了點和圓的位置關系、切線長定理、三角形內切圓和外接圓，并且復習了一些典型習題。

小結問題2：研究一個圖形（如點、線或三角形）與圓的有關位置關系，你積累了哪些經驗？

預設：如研究圖形的組成元素與圓的組成元素之間的位置關系，這些關系對應著一定的數量關系。

小結問題3：四邊形一定有內切圓嗎？四邊形一定有外接圓嗎？如果一個四邊形既有內切圓，又有外接圓，那這個四邊形的邊、角之間有什么樣的關系？請有興趣的同學課后深入研究。

預設：四邊形不一定有內切圓，也不一定有外接圓。如果一個四邊形既有內切圓，又有外接圓，這樣的四邊形對角互補，對邊之和相等。

二、教學立意的進一步闡釋

1.選編好的問題，讓畫圖活動驅動復習進程

關于如何選編“好的問題”驅動教學進程，文獻[3]中提出“好的問題”要有“數學味”“盡量串聯整節課”。想來，本文關注的這節復習課各個環節的問題設計也追求了上述特點。比如，開課階段，筆者安排了一道“結構不良問題”（過一點，畫出圓的切線），對于思維不嚴謹的學生，教師可以先安排小組交流，以完善他們的認知，然后通過全班學生交流，展現學生對這個問題的“完整思考”；在后續復習進程中，筆者始終圍繞“活動1”畫出的圖形進行變式、改編，整節課都圍繞著開課階段得出的基本圖形漸次展開、由淺及深，實現了好的問題（伴隨畫圖活動）驅動整節課的復習進程。

2.預設開放式問題，用相機追問凸顯復習深度

鄭毓信教授多年前就倡導“從開放題走向開放式教學”。然而我們看到的不少復習課中，由于使用了大容量的習題單式的導學案，使得復習課成為“一題接著一題”的習題講評課，雖然在一些習題的講評過程中有些師生的對話，但大多停留在“師問生答”的較低層面，整體上看，教學過程是比較封閉的。為了讓教學從封閉走向開放，我們在上述課例的教學設計中安排了多處的“開放式問題”，除了上述提到的開課階段的“結構不良問題”（也可看成開放式問題）外，“問題2”“問題3”“問題4”在題干呈現之后，都安排了開放式問題，促進了后續的開放式教學。值得一說的是，這些開放式問題，并不是簡單放手，也不是上課時任由學生“踩著西瓜皮，滑到哪里是哪里”，而是需要教師在課前充分預設學生可能的回答以及教師要給出什么樣的點評或追問，特別是通過恰到好處的追問，凸顯和追求復習的深度。

3.構思小結問題，幫學生梳理、回顧復習內容

復習課的教學時間常常難以把控，往往因為有些較難問題的課堂展示、點評用時偏多，就會擠占課堂小結的時間。筆者建議，教師在課前就要精心構思“小結問題”，讓小結問題幫助學生梳理回顧整節復習課的內容。特別地，要通過“小結問題”與前面的各個復習課進行關聯、呼應，使其成為復習課不可或缺的重要環節。如上文“小結問題1”安排學生回顧本節課是如何復習的，“小結問題2”讓學生梳理、積累研究幾何問題的方法與經驗。當然，作為必要的拓展與研究展望，筆者還預設了“小結問題3”，讓學余有力的學生繼續探究、挑戰“既有內切圓又有外接圓的四邊形的性質”。需要指出的是，像“小結問題3”這樣的課前預設，也需要像“課中”很多預設的追問一樣，根據教情、學情相機呈現，有的放矢。想來，這也是“預設要大于生成”的一種備課追求吧。

【參考文獻】

［1］中華人民共和國教育部.義務教育數學課程標準（2022年版）［M］.北京：北京師范大學出版社，2022（4）．

［2］王強.基于確定性下的尺規作圖［J］.中學數學雜志，2021（8）：58-61．

［3］劉東升.我們需要怎樣的“問題”驅動課堂——由美國莎維女士執教的函數圖像課說起［J］.教育研究與評論（課堂觀察），2016（11）：65-68.

［4］鄭毓信.“開放的數學教學”新探［J］.中學數學月刊，2007（7）：1-4．

本文系江蘇省教育科學“十四五”規劃課題“高質量發展視域下‘三學’立人的實踐研究”（課題編號：TSXM/2021/06）階段性研究成果。

（作者單位：1.江蘇省南通市啟秀中學；2.江蘇省南通市教育科學研究院）