基于黎曼流形的健身APP風險度量方法

摘 要 隨著智能設備的普及，其應用系統已成為惡意軟件攻擊的主要目標，存在巨大的網絡安全隱患。健身App因其獲取數據的隱私性和敏感性，面臨的數據安全問題更加嚴峻，其安全度量模型成為解決這一挑戰的關鍵點。目前的安全度量模型多數基于靜態特征構建，未能全面考慮智能設備的動態網絡行為。為了彌補這一不足，提出一種基于網絡行為的健身App安全度量模型，運用協方差矩陣對網絡空間進行轉換，提高了對惡意軟件攻擊識別的準確率，根據健身App的動態網絡行為特征，更全面地揭示了其安全狀態，同時結合黎曼度量，有效描述了網絡安全風險，并計算其值，從而構建出一個基于惡意軟件攻擊識別與黎曼流形的風險度量模型，以實現更安全的數據保護。

關鍵詞 數據安全；網絡行為；黎曼流形；風險度量模型；協方差矩陣

中圖分類號：G804.2 學科代碼：040302 文獻標志碼：A

DOI：10.14036/j.cnki.cn11-4513.2024.05.004

Abstract With the widespread adoption of smart devices， they have become prime targets for malicious software and malicious traffic attacks， posing significant cybersecurity risks. Fitness apps， due to the privacy and sensitivity of the data they acquire， face even more serious data security issues， making their security measurement models a key hotspot for addressing this challenge. Existing security measurement models are mostly based on static featu-res and fail to fully consider the dynamic network behavior of smart devices. To address this limitation， this paper proposes a network behavior-based security measurement model for fitness apps， utilizing covariance matrices to transform the network space， thereby enhancing the accuracy of malicious attack detection. By considering the dynamic network behavior characteristics of fitness apps， it more comprehensively reveals their security status. Furthermore， by combining Riemannian metrics， it effectively describes network security risks and computes their values， thus constructing a risk measurement model based on attack recognition and Riemannian manifolds to achieve more secure data protection.

Keywords data security; network behavior; Riemannian manifold; risk measurement model; covariance matrix

在當前的數字化背景下，智能設備，尤其是安卓系統，面臨著日益復雜的網絡安全挑戰。由于其開放性和應用的多樣性，用戶能夠下載來自不同信息源的應用程序，這為惡意軟件提供了可乘之機，使其更容易植入安卓系統并進行各種風險性操作。因此，安卓系統應用的安全性問題逐漸成為關注焦點。

健身App作為健康管理的重要工具，其具有為用戶制定健身計劃的功能，需要獲取用戶的一些個人隱私信息。然而，其對中心服務器的頻繁訪問容易遭到惡意軟件的攻擊，從而導致隱私數據被竊取，進一步致使用戶隱私泄露、運動數據篡改、系統和服務器受損等，嚴重影響用戶體驗和健康數據的可信度。

本研究以健身App使用場景為背景，結合2020年加拿大網絡安全中心與加拿大網絡安全研究所提供的安卓惡意軟件數據集（Canadian Institute for Cyber-security project in collaboration with Canadian centre for cyber security for Android Mavware in 2020，CCCS-CIC-AndMal-2020）關于安卓系統惡意軟件的分類和行為特征信息，研究基于網絡行為的安全風險度量方法，將攻擊識別與風險度量相結合，度量了網絡安全的累積風險，有效應對潛在的惡意軟件威脅，為用戶提供更安全、可靠的健康管理服務。

常見的度量方法主要有3類：評估體系模型、邏輯推理模型和數據分析模型。1）評估體系模型包括構建指標體系、賦予指標權重及計算風險值。例如：Yuan等學者提出了基于層次分析法的網絡效能評估方法［1］；Xu等學者建立了威脅與漏洞識別模型［2］；Zhao等學者提出的多維分析法，實現了指標賦權的主觀性優化［3］。2）邏輯推理模型是根據先驗信息對系統進行感知與評估［3］。例如：王增光等學者提出了基于隱馬爾可夫模型的網絡安全評估方法［4］；Yu等學者構建了網絡安全評估指標體系［5］；Zhao等學者提出了基于拒絕服務（DOS）證據理論的分布式拒絕服務（DDoS）分層網絡威脅態勢評估方法，通過加權算法獲得網絡當前風險［6］。3）數據分析模型主要采用機器學習或深度學習對數據進行分類處理。例如：Gao等學者通過選擇合適的徑向基函數（RBF）模型，得出了最佳參數［7］；嚴俊龍等學者提出了基于映射歸納與支持向量機（SVM）相結合的網絡安全狀態預測模型，并進行分布式訓練，優化了模型的訓練速度［8-9］；Ajeetha等學者使用樸素貝葉斯與隨機森林2種分類器處理混淆矩陣，獲得了比當前更優的算法［10］；Shende等學者利用長短期記憶法與攻擊檢測相結合，實現對網絡狀況的觀察與識別［11］。

本研究的主要貢獻在于：1）針對現有度量方法存在主觀性較強、度量精度較低的問題，提出了安全風險值的計算方法，利用協方差矩陣進行網絡流量特征的空間轉換，提高了識別效率與準確率，并通過實驗驗證了使用黎曼度量計算安全風險的有效性；2）針對當前網絡風險評判標準不統一的問題，提出了將正常狀態下的網絡流量的黎曼均值作為網絡安全風險度量基線，體現了使用黎曼度量進行計算的優越性與有效性；3）針對持續攻擊產生的累積風險，提出了風險累積系數，并列出了計算方法和綜合行為風險的計算公式，同時提出了基于協方差矩陣特征空間變換與極限樹相結合識別惡意軟件攻擊的方法，提高了健身App平臺對惡意軟件的防御能力。

1 健身App風險分析

以下從健身App的架構特點和數據特點兩方面分析健身App當下面臨的風險。

1.1 健身App架構分析

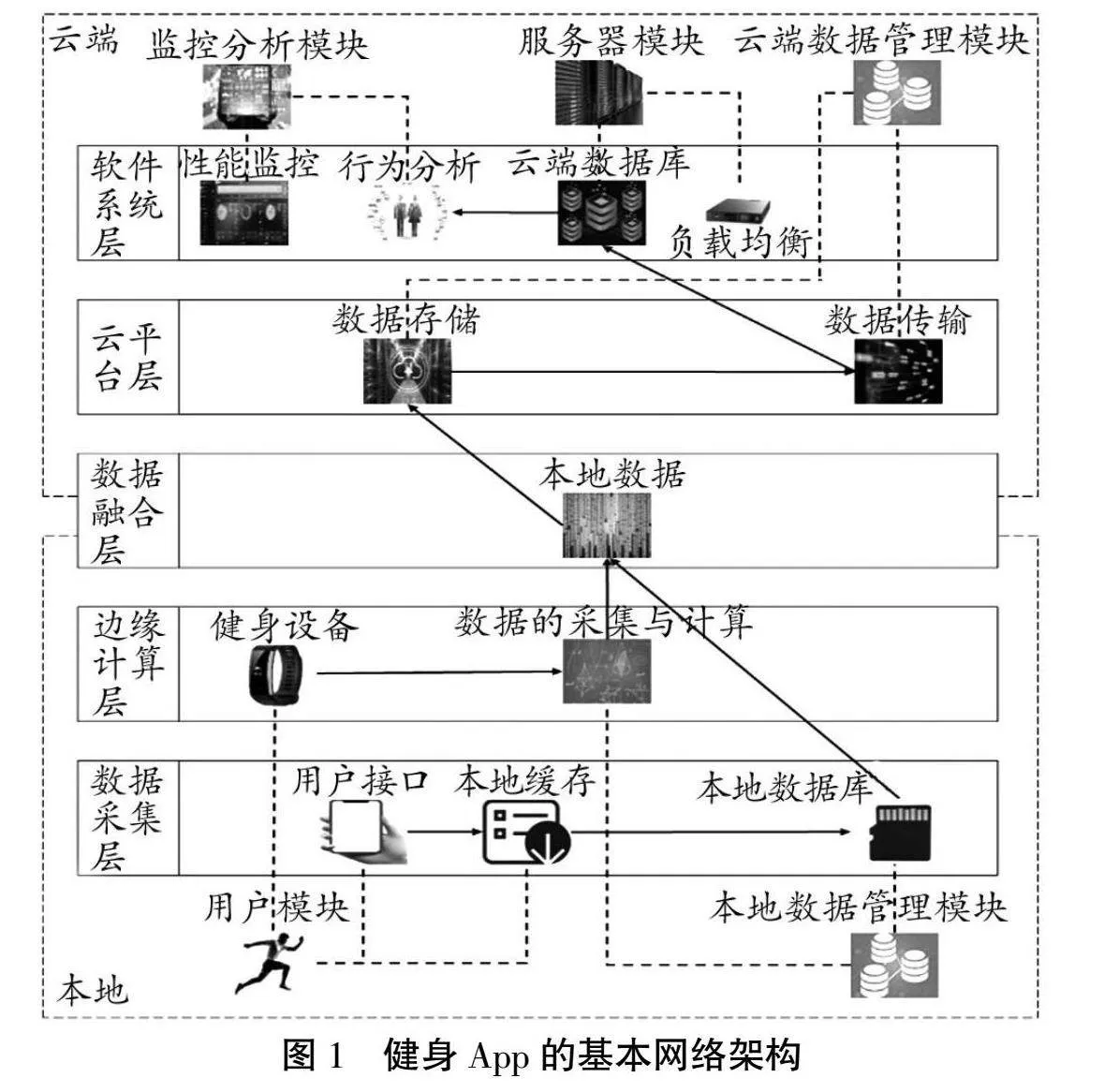
健身App的基本網絡架構如圖1所示，分為用戶端和云端兩部分，一共5層：數據采集和邊緣計算層屬于本地端，包括用戶端和本地數據管理兩部分；云平臺層和軟件系統層屬于云端，包括服務器、云端數據和監控分析三部分；本地端模塊和云端模塊通過數據融合層進行交互。

從健身App網絡架構可知，本地端采集的個人身份信息、大量運動數據等隱私數據基于信息安全會分散存入不同云端服務器，這為惡意軟件的攻擊提供了可乘之機，而運動數據實時上傳，又為DDoS攻擊提供了便利。正是因為健身App這種裝機量大、服務器多、數據傳送實時的特點，使得其更容易遭到惡意軟件的滲透。因此，形成適于對健身App網絡環境安全評估的方法尤為急迫。

1.2 健身App數據安全分析

健身App作為一種通過智能手機或健身手表等設備，輔助用戶記錄和分析個人健康和運動數據的應用程序，其數據特征包括用戶注冊信息、健身手表數據、健身App運動數據、身體基本信息等，諸如性別、年齡、身高等身體數據，運動時間、運動類型、運動地點等運動數據，甚至血壓、心率、體脂率等健康敏感數據。而對于需要調整飲食、作息等個人習慣來增強健身效果的特殊用戶，健身平臺需要獲取其每日食譜、作息安排等隱私數據，甚至還需知曉用戶的病史。這些數據都是與用戶密切相關、且需要保密、不能被第三方竊取的隱私敏感信息［12］。

健身App涉及用戶的個人隱私和健康信息種類多、基數大，所以需要嚴格的隱私保護措施來確保用戶數據的安全性和隱私性，防止數據泄露和濫用。

2 基于黎曼流形的網絡安全風險度量

針對健身App隱私數據容易被惡意軟件攻擊、竊取等安全問題，本研究選取了網絡安全風險度量的概念。網絡安全風險度量即量化網絡系統風險以對網絡系統安全狀態［13］進行精準描述。本研究中通過協方差矩陣變換豐富網絡特征，并將網絡流量特征映射到高維空間，根據安全狀態下的網絡流量確定安全基線，計算當前網絡狀態與安全基線之間的黎曼距離來判定攻擊軟件的種類。同時，通過計算累積風險值，對當前網絡狀態進行度量和描述。

2.1 空間轉換與協方差矩陣

惡意軟件通常會引起異常的網絡流量，其與正常流量相比，存在異常的帶寬利用率、數據包頻率、連接持續時間等差異。通過對流量數據進行時序分析，可以檢測出突發性的流量增長，從而發現惡意軟件。本研究運用了協方差矩陣，通過分析網絡流量特征之間的關系提高識別惡意攻擊的準確率。

按照時間段對網絡流量數據進行劃分，對網絡特征之間進行協方差計算，協方差計算公式如下。

cov（X，Y）=E［（X-E（X））（Y-E（Y））］ 1）。

每個時間段內的數據為一個樣本，對在初始情況下具有n個特征的樣本，通過空間轉換成一個n×n的協方差矩陣對該樣本進行刻畫。高維隨機變量的協方差計算公式如下。其中，xi與xj分別表示高維向量的某2個隨機變量，假設一共存在k個實例，則xim中的m表示第m個實例，如公式（2）所示。

cov（xi，yi）=∑k m=0（x-E（x））（xjm-E（xj））2）。

在分析網絡流量時，每個隨機變量表示網絡流量的一個特征，而k個n個特征的網絡流量的描述則可以通過以下的n×n的協方差矩陣進行描述，如公式（3）所示。

3）。

協方差矩陣的對角線上的元素為同一特征值的方差，表示該特征的離散程度，而其他元素則表示不同特征值之間的協方差，表示2個不同特征之間的相關性。

2.2 基于黎曼度量的網絡安全風險計算方法

Zhao等學者提出，可以基于攻防對抗效用構建網絡安全評估框架［14］。還有學者根據網絡行為效用計算原理采用微分流形［15］對網絡場景進行了刻畫，形成了網絡行為客觀度量方法［16］。本研究通過協方差矩陣對網絡特征值進行處理，使用協方差矩陣對網絡狀態進行描述，通過對協方差矩陣的對角線增添微小擾動可實現協方差矩陣的正定性。本研究的網絡安全狀態描述是基于對稱正定流形［17］形成的（簡稱SPD流形）。

由n×n的矩陣構成的空間為一個具有離群特征的黎曼流形，因而可以使用黎曼測地線對空間中點的距離進行計算，該距離即當前網絡空間狀態與預定的安全狀態［18］之間的差距。對稱正定流形的黎曼距離計算方法最常見的是仿射不變度量，如公式（4）所示，所以本研究的實驗也采用該方法。

δL （X，Y）？劬‖log（X）- log（Y）‖ 4）。

在估算安全風險時，安全風險度量基線被用于對比的標準狀態。安全風險度量基線的設定值為無攻擊、正常運行狀態下的特征平均值作為安全風險度量基線，與該基線的差距表示安全風險值。

本研究通過采集大量安全狀態下的網絡數據以獲得多組對應網絡安全狀態特征值的協方差矩陣。對多組協方差矩陣進行黎曼矩陣的計算以獲得網絡安全狀態的基準值。根據黎曼度量計算當前網絡狀態特征值的協方差矩陣與基準線矩陣的黎曼距離。對于1組含有k個n×n的SPD流形［19］的正定對稱矩陣的數據集合（xi∈ sym+d），流形的每一點的風險值通過公式（5）計算。

Riski=δ（xi，b） 5），

式中：δ表示SPD流形的黎曼測地線的計算函數； b表示安全度量基線的黎曼均值。

2.3 安全風險度量模型

由于惡意軟件攻擊的安全風險是一個持續的過程，因而安全風險也是一個逐漸積累的過程，本研究中的風險累積系數η用于對當前網絡風險進行描述，隨著攻擊的持續，網絡服務資源逐漸被耗盡，風險累積系數隨之增大，某一時刻（t）的風險累積系數計算方法見公式（6），式中：a=2。

ηt=log a（∑t-1i=sRiski） 6）。

當前的實時安全風險值由自檢測到網絡攻擊開始的當前網絡協方差矩陣與安全基線間距離和取對數得出，取對數是為了確保風險累積系數的增長幅度可控，使ηt可以增長到過大的數值。某一時刻（t）的綜合風險值由公式（7）計算得出。

Rt=（1+ηt ）Riskt7）。

綜合風險值由累積系數與當前安全基線共同決定，在受到特定攻擊時，Riskt的值變化幅度穩定在非常小的范圍內，因而在相同攻擊階段，Rt可以很好地體現出ηt的累積變化，在不同攻擊狀態下，Rt可以很好地體現出Riskt的屬性。

3 實驗數據分析

3.1 數據來源

本研究使用CCCS-CIC-AndMal-2020［20-21］數據集進行分析驗證。該數據集包含14個惡意軟件類別，其中有廣告軟件、后門程序、文件感染者、無類別、潛在有害應用程序、勒索軟件、風險軟件、恐嚇軟件、特洛伊木馬等，包括內存、應用程序編程接口（API）、網絡、電池、日志工具（Logcat）和進程六大類共144個特征，可以模擬健身App可能遇到的不同類型的網絡安全威脅，而數據集中的特定惡意軟件類別，如潛在有害應用程序和零日攻擊，更是直接與健身App所面臨的潛在網絡安全威脅相關，非常貼近健身App的實際情境。

3.2 實驗流程

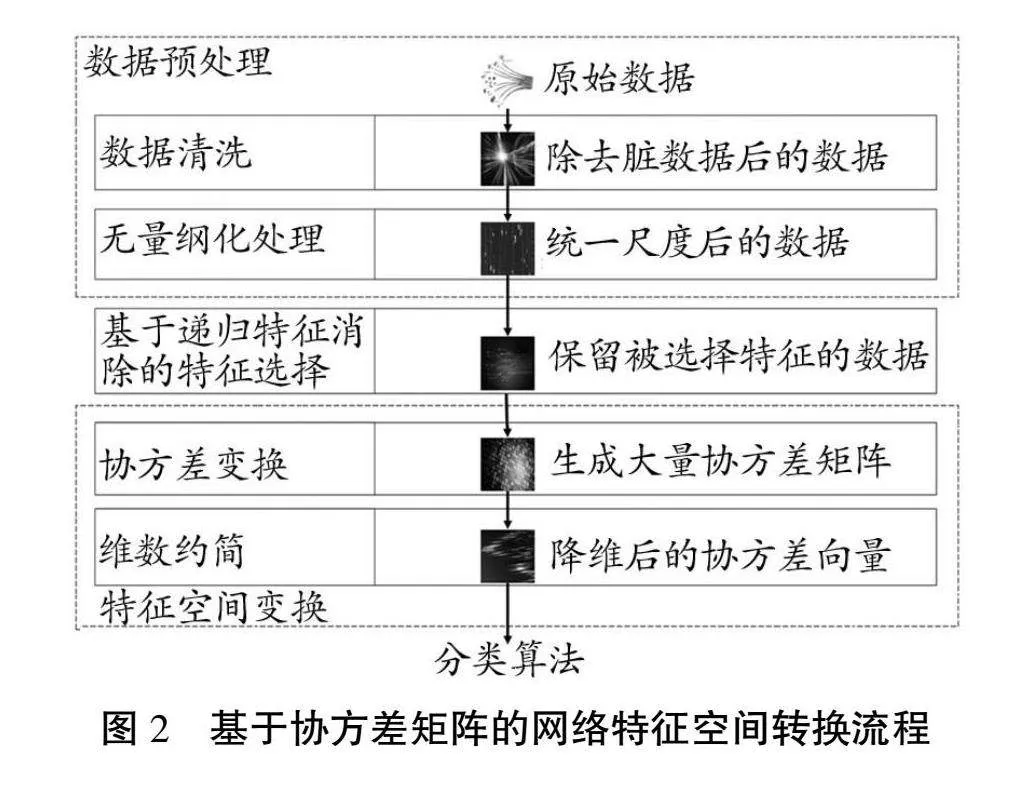
網絡流量數據特征眾多，本研究以CCCS-CIC-An-dMal-2020數據集提供的144個特征變量為基準進行處理，數據處理流程如圖2所示。

3.2.1 數據預處理

在本階段首先對數據進行篩選審核以進一步進行數據挖掘，本階段包括數據清洗和特征選擇。首先對數據進行清洗與無綱量化處理，將無法訓練的“臟”數據進行清洗。其次，如“Hash”“Family”等特征不具有通用意義，因而需要對此類特征進行人工刪除，避免其影響模型有效性。本研究通過隨機森林選擇對結果影響較大的20個特征值及其權重，如圖3特征權重所示，后續實驗將以這20個核心特征作為基礎。

3.2.2 協方差數據處理

使用協方差矩陣對網絡流量進行描述，以200組流量數據為1組，計算對應于一個時間段的網絡流量特征的協方差矩陣，該矩陣選取20個特征作為網絡流量的描述矩陣，以實現升維，將原本20個特征值增長至400個。由此可以證明，對于n條d個數據集合，其協方差矩陣是一個d×d的矩陣A。該矩陣A的對角線數值是原有指標的方差，體現了每個指標的離散程度，可用來表征不同攻擊可能會導致的某些指標離散程度的變化；其非對角線數值是2個隨機變量的協方差，可以反映這2個變量的總體誤差以及這2個變量的相關性。因此，矩陣A是對稱的。為了降低數據的計算、存儲成本，根據矩陣A的對稱性，本研究將處理后的數據又進行降維處理，將d×d的數據壓縮至d（d + 1）/2的向量。

實驗采用邏輯回歸、隨機森林決策樹以及SVM算法對處理前與處理后的數據進行分類識別，并對不同分類算法的識別結果進行橫向對比。同時對網絡流量數據得出的協方差分別計算黎曼距離與歐式距離，使用K鄰近（KNN）算法根據2類距離對攻擊進行分類。

3.2.3 網絡安全基線

由于協方差矩陣具有非負定對稱特點，本研究通過對協方差矩陣的對角線數值增加微小正向擾動以確保其正定性，從而獲取SPD流形，根據協方差矩陣度量基線計算對應的協方差矩陣組，增加相應擾動，并計算黎曼均值，將結果設定為安全風險度量基線。

3.2.4 安全風險值度量

本實驗通過向正向流量中分批次插入惡意攻擊數據模擬受到多種攻擊的網絡流量狀態。整個模擬過程包含53 439條流量數據，通過將當前網絡狀態的協方差矩陣作為輸入數據，并使用Extra Tree對網絡攻擊進行識別，可以計算出網絡流量協方差與網絡安全基線的黎曼距離，進而得出實時網絡安全風險值。在攻擊持續時間內，根據風險累積系數可以計算出綜合網絡安全風險值。

3.3 結果與分析

3.3.1 邏輯回歸算法、隨機森林算法和SVM算法

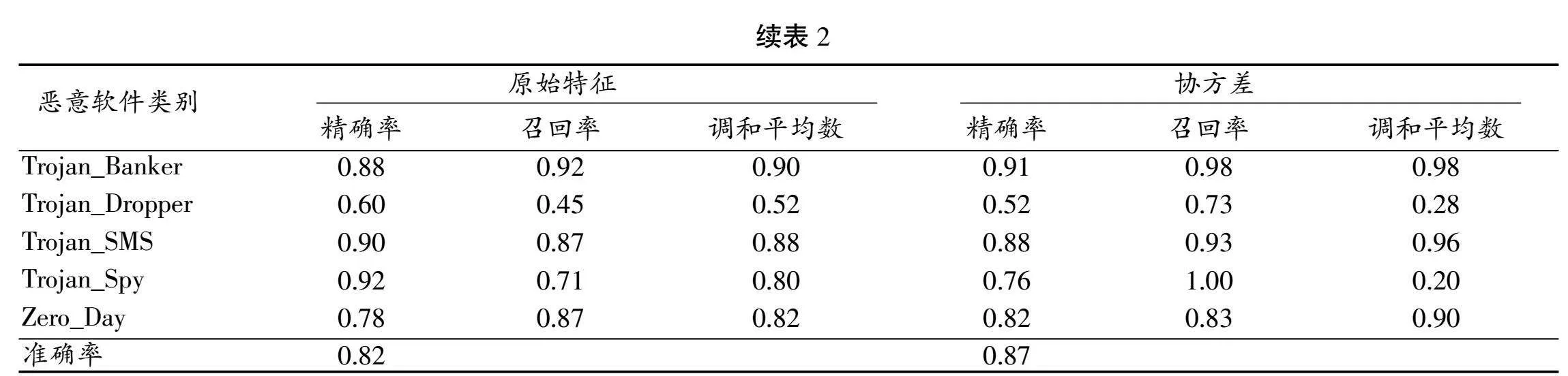
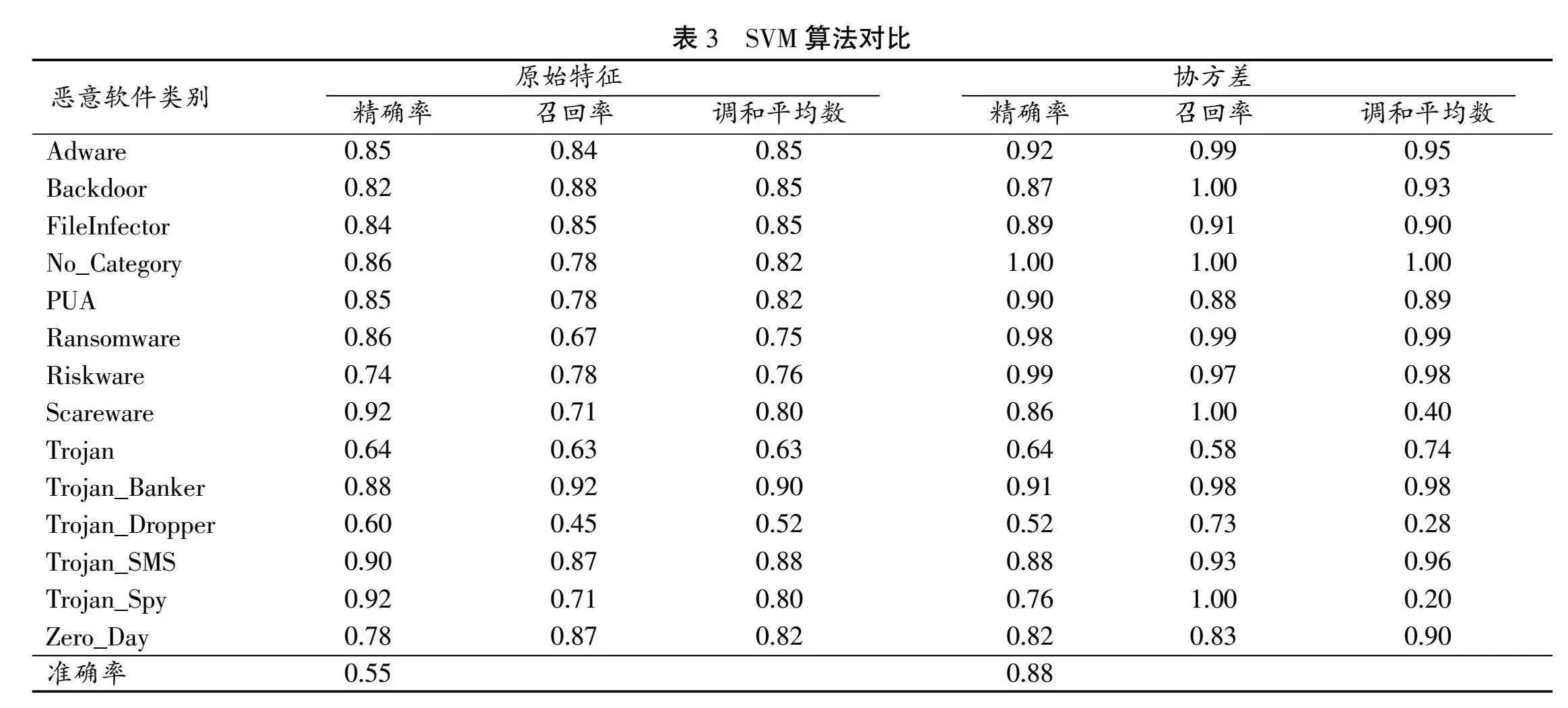
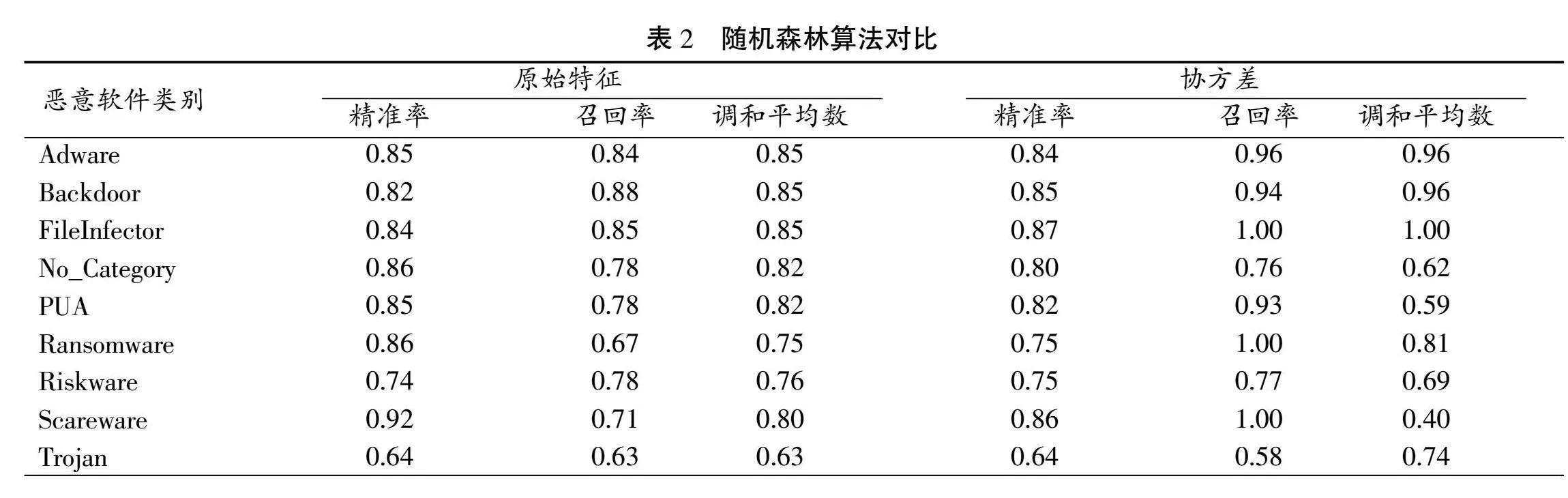
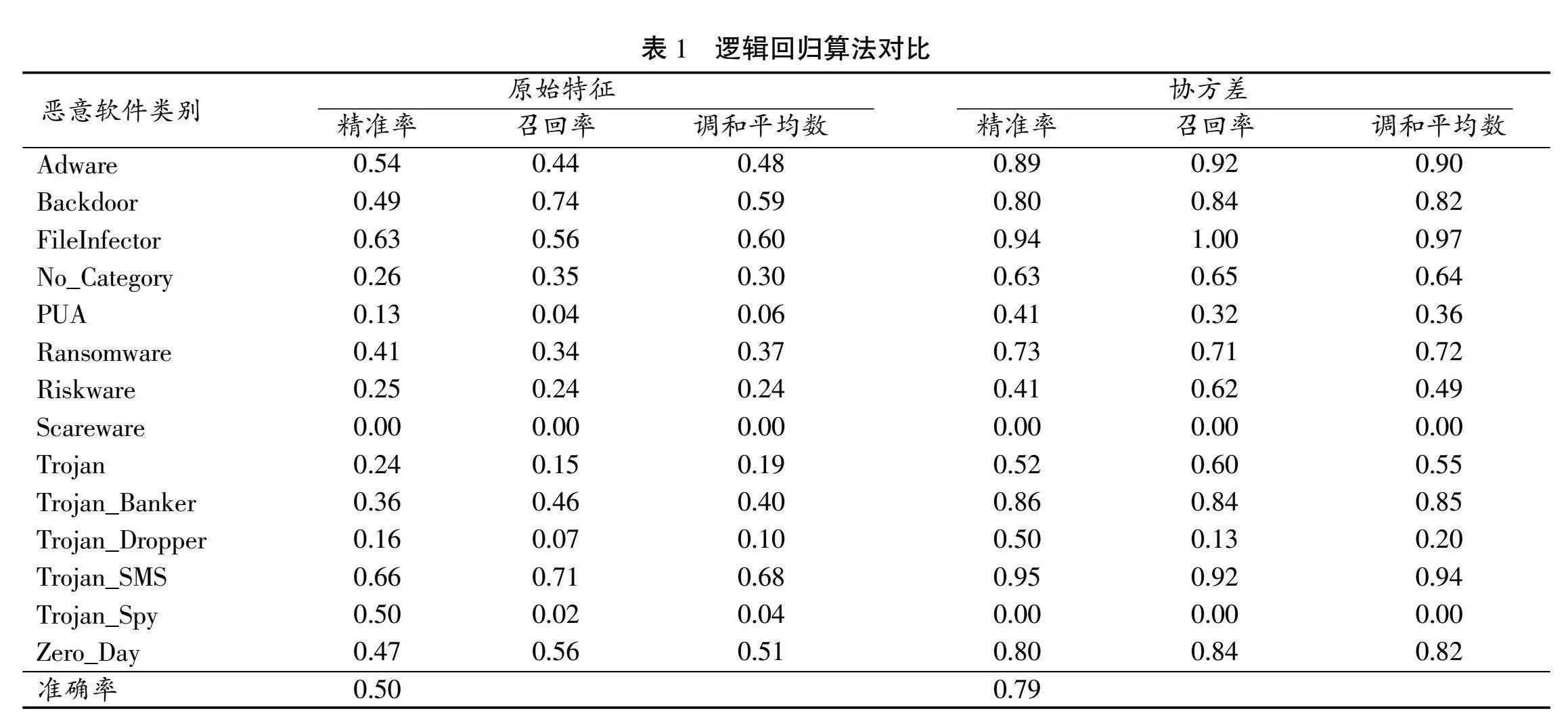
使用邏輯回歸算法、隨機森林算法以及SVM算法對原始數據和協方差變換后的數據進行對比，識別效果如表1、表2和表3所示。

3種機器學習算法均對數據集CCCS-CIC-And-Mal-2020的14類惡意軟件進行分類，并訓練相應模型，以及采用精確率、召回率和精確率與召回率的調和平均數作為評判指標。

由上表數據可知，使用協方差變換之后，機器學習算法對大部分網絡攻擊的識別的效果更佳，與未采用協方差變換的情況相對比，在良性No_Category以及PUA軟件攻擊的識別方面采用協方差變換有了大幅度的改善。

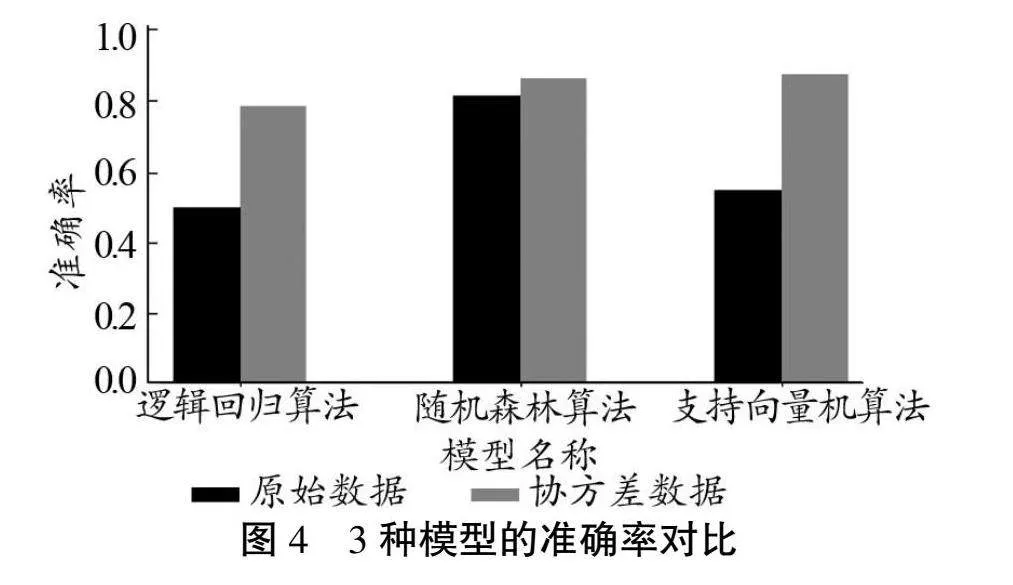
圖4為3種算法的準確率對比圖匯總，從中可知，不同類別算法對使用協方差矩陣進行數據變換后的分類效果明顯更好。

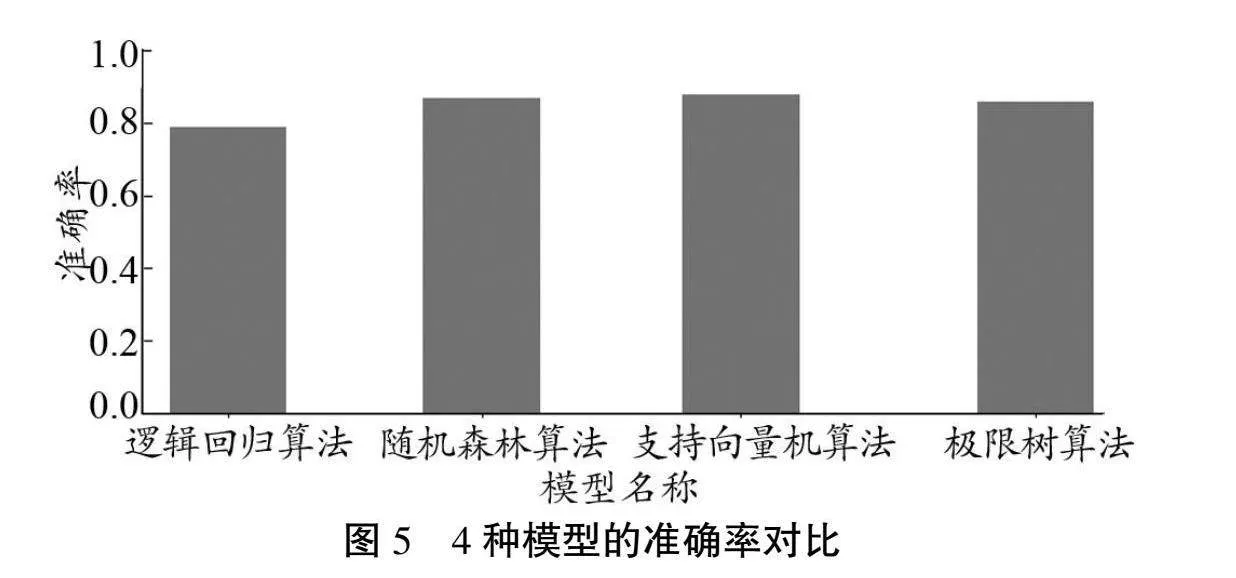
將經過變換后的網絡安全特征協方差矩陣作為數據，分別使用邏輯回歸算法、隨機森林算法、SVM算法及極限樹算法分別進行攻擊識別，識別結果如圖5所示。

從圖5可知，SVM算法在識別攻擊時的效果明顯好于邏輯回歸算法，略好于隨機森林算法和極限樹算法。這說明使用SVM算法可以非常準確地對網絡攻擊流量進行分類，可以為后續的累積安全風險度量提供有力支撐。

3.3.2 KNN

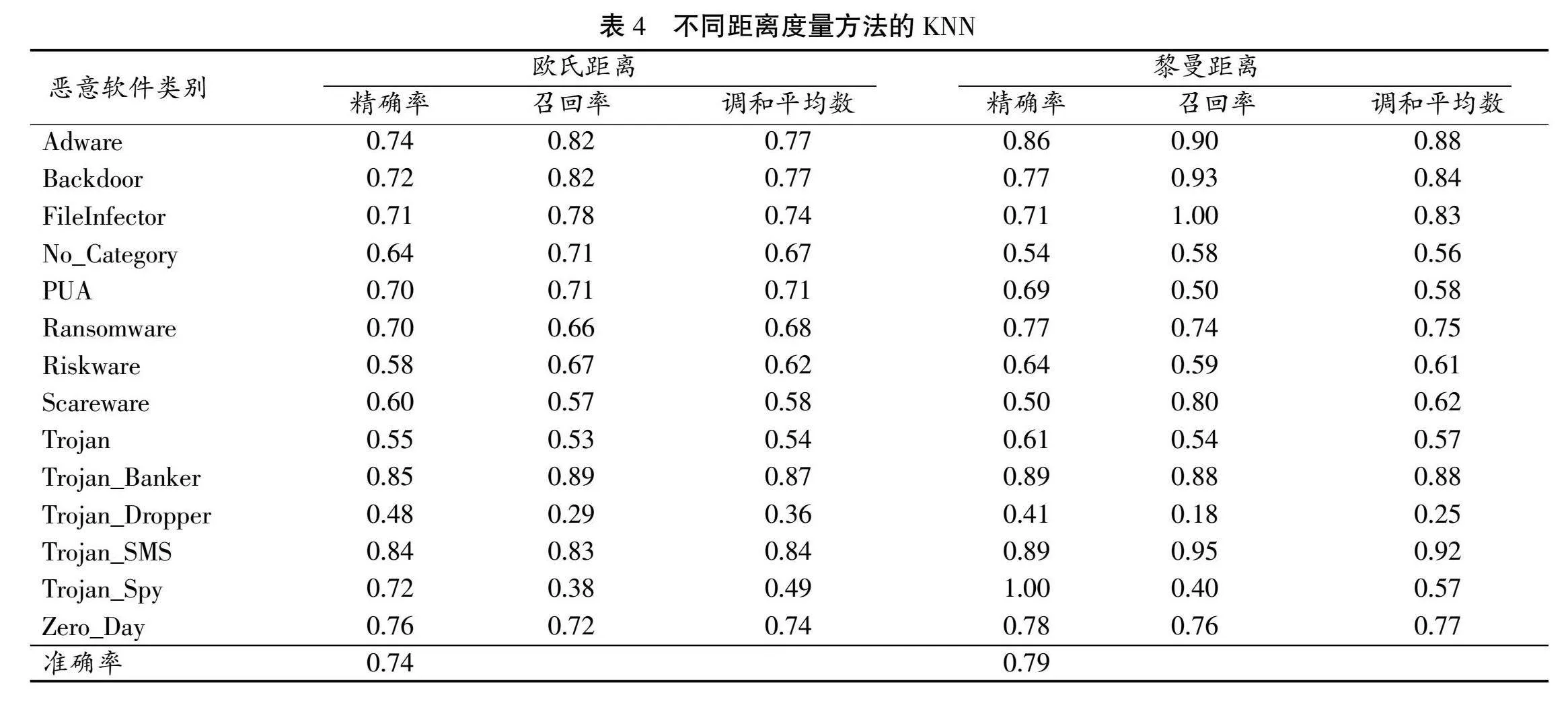
利用KNN算法對歐式距離和黎曼距離對惡意軟件分類的效果進行對比，結果如表4所示。

由實驗結果可知，基于黎曼距離的KNN算法的分類效果更精確，說明黎曼距離能有效反映SPD流形的狀態差異，從而證明了黎曼度量能用于網絡安全風險值的計算。

3.3.3 風險計算

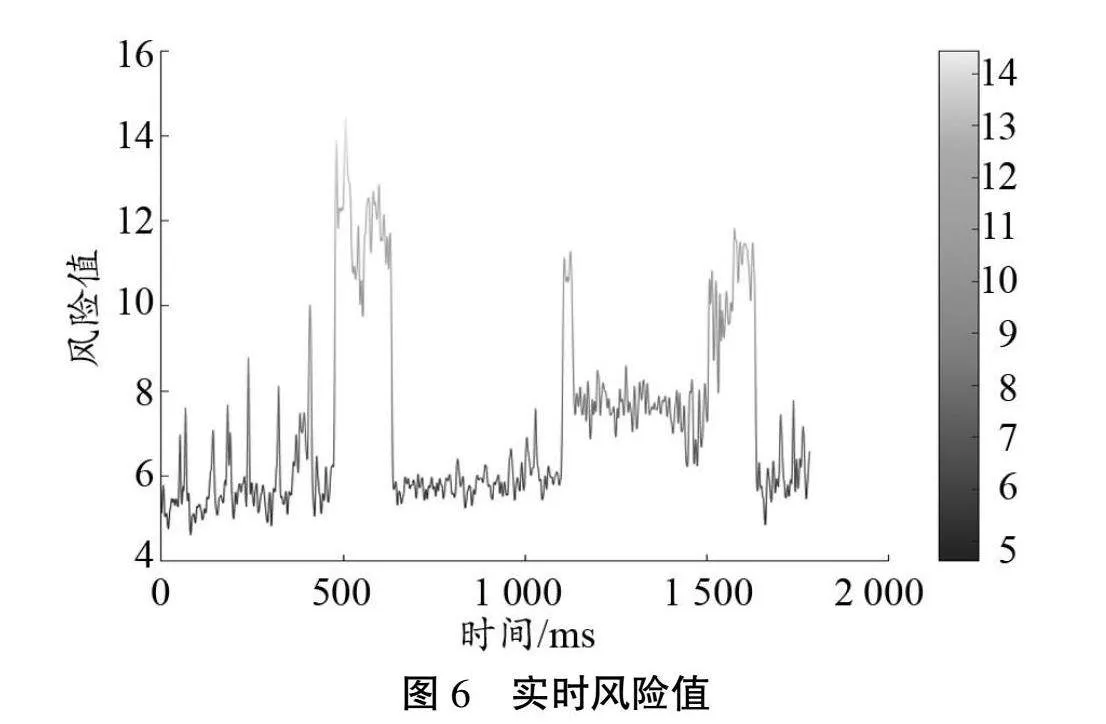
在正常流量中分批插入惡意攻擊數據模擬攻擊行為，針對整個流量數據，根據公式（6）計算得出的實時風險值如圖6所示。

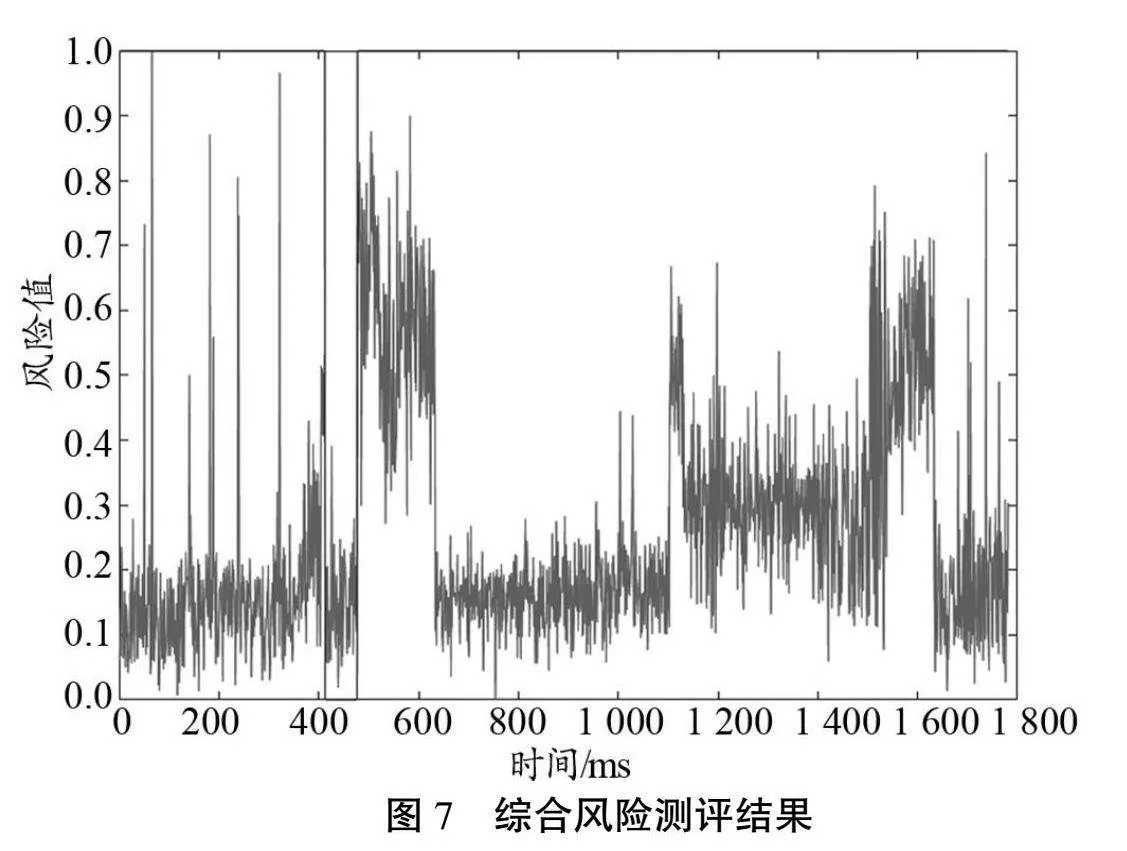
通過識別惡意攻擊類型并確定攻擊持續性，針對惡意攻擊持續時間段內的全部流量數據，根據公式（7）計算綜合風險測評結果如圖7所示。

從圖7可知，在受到網絡攻擊時，網絡實時安全風險值會明顯增大，而在安全狀態下會出現一個比較小的安全風險值，該風險值的變化與攻擊與否相吻合。同時在計算安全風險值時，健身App處于無監督狀態，這也說明可以通過這種度量方法對未知的惡意軟件攻擊風險進行度量。而累積風險是在考慮實時安全風險的基礎上，增大了持續攻擊所產生的累積風險的影響，從而可以計算出一個綜合的網絡安全風險值。從圖7可知，在攻擊初期的網絡安全風險的大小主要由實時安全風險決定，但隨著攻擊時間的持續，攻擊持續時間對風險值的影響將越來越大，這也與真實環境下惡意攻擊的特點［22］相吻合。

通過實驗，充分證明了使用協方差與極限樹結合識別攻擊的算法的有效性，同時也證明了使用黎曼度量計算實時網絡安全風險值的有效性，以及結合累積風險計算綜合網絡安全風險的合理性。

4 結論

針對健身App存在的容易被惡意軟件滲透和攻擊而引發的信息安全問題，本研究提出了一種安全風險值的度量方法，通過協方差矩陣處理數據，進行網絡流量特征的空間轉換，在邏輯回歸算法、隨機森林算法和SVM算法的驗證下，模型的準確率分別提高了29%、5%和33%，驗證了協方差矩陣處理數據的優越性，使健身App平臺能在網絡攻擊初期以及攻擊過程中作出風險預警，盡早地對用戶數據進行防護，從而盡可能地減少損失。本研究提出了使用正常狀態下的網絡流量的黎曼均值作為網絡安全度量基線，采用KNN算法，選擇歐拉度量和黎曼度量2種度量方法進行測試。其中，黎曼度量的模型準確率提高了5%，驗證了使用黎曼度量評估安全風險的有效性，為健身App平臺的安全維護提供了有效標準。最后，本研究提出了風險累積系數，并列出了計算方法和綜合行為風險的計算公式，通過將53 439條數據種插入惡意攻擊軟件，有效地模擬出真實環境下的惡意攻擊，得出該模型的實時風險和綜合風險的計算結果，與真實環境被惡意攻擊的特點吻合，可以為健身App實際開發提供良好的參照。

參考文獻：

［1］ YUAN Z， YAO S， XIA C， et al. Network efficacy evaluation based on AHP for network security situation assessment ［C］//Proceedings of the 2016 6th International Conference on Mach-inery， Materials， Environment， Biotechnology and Computer.Paris： Atlantis Press， 2016：797-800.

［2］ XU N， ZHAO D. The research of information security risk asses-sment method based on AHP［J］. Advanced Materials Resear-ch， 2011， 187： 575-580.

［3］ ZHAO X， XU H， WANG T， et al. Research on multidimensional system security assessment based on AHP and gray correlation ［C］///Proceedings of Trusted Computing and Information Securi-ty： 13th Chinese Conference， CTCIS 2019. Shanghai： Springer Singapore， 2020： 177-192.

［4］ 王增光，盧昱，趙東昊. 基于隱馬爾科夫模型的網絡安全風險評估方法［J］. 空軍工程大學學報（自然科學版），2019，20（3）：71-76.

［5］ YU J， HU M， WANG P， et al. Artificial intelligent techniques and its applications［J］. Journal of Intelligent & Fuzzy Systems， 2018， 34： 861-869.

［6］ ZIHAO L， BIN Z， NING Z， et al. Hierarchical network threat situation assessment method for DDoS based on DS evidence theory［C］//Proceedings of 2017 IEEE International Conference on Intelligence and Security Informatics （ISI）. Beijing： IEEE，2017： 49-53.

［7］ GAO H S， GUO A L，YU X D， et al. RBF-SVM and its application on network security risk evaluation ［C］//Proceedings of the 2008 4th International Conference on Wireless Communications， Netw-orking and Mobile Computing. Shanghai： IEEE， 2008： 36-39.

［8］ HU J， MA D， LIU C， et al. Network security situation prediction based on MR-SVM ［J］. IEEE Access， 2019， 7： 130937-130945.

［9］ 嚴俊龍，李鐵源. 基于 SVM 的網絡安全風險評估模型及應用［J］. 計算機與數字工程，2012，40 （1）： 82-84.

［10］ AJEETHA G， PRIYA G M. Machine learning based DDoS atta-ck detection［C］//Proceedings of the 2019 Innovations in Power and Advanced Computing Technologies （i-PACT）.Pisca-taway： IEEE：i-PACT， 2019： 1-5.

［11］ SHENDE S. Long short-term memory （LSTM） deep learning method for intrusion detection in network security［J］. Internat-ional Journal of Engineering Research， 2020， 9（6）： 1615- 1620.

［12］ 周志雄，唐子人，賈曉蕓，等. 全民健身信息服務平臺關鍵技術研究［J］. 首都體育學院學報，2023，35（3）：257-266.

［13］ KUMAR R， GUPTA D. Software bug prediction system using neural network［J］. European Journal of Advances in Engineer-ing and Technology， 2016， 3（7）： 78-84.

［14］ ZHAO X， ZHANG Y， XUE J， et al. Research on network risk evaluation method based on a differential manifold［J］. IEEE Access， 2020， 8： 66315-66326.

［15］ 詹漢生. 微分流形導引 ［M］. 北京：北京大學出版社，1987：8-12.

［16］ ZHAO X， CHEN Q， XUE J， et al. A method for calculating network system security risk based on aLie group［J］. IEEE Access， 2019， 7： 70610-70623.

［17］ 陳維桓. 微分流形初步［M］. 2 版.北京：高等教育出版社， 2001： 35-38.

［18］ YI B， CAO Y， SONG Y. Network security risk assessment model based on fuzzy theory ［J］. Journal of Intelligent and Fuzzy Systems， 2020， 38（4）：3921-3928.

［19］ 紀永強. 微分幾何與微分流形［M］. 北京：高等教育出版社， 2000： 77-90.

［20］ KEYES D S ， LI B ， KAUR G ，et al. EntropLyzer： Android malware classification and characterization using entropy analysis of dynamic characteristics［C］//Conference on Reconc-iling Data Analytics， Automation， Privacy， and Security： A Big Data Challenge.Canada： IEEE， 2021：1-2.

［21］ RAHALI A ， LASHKARI A H ， KAUR G ，et al.DIDroid： Andr-oid malware classification and characterization using deep image learning［C］// Proceedings of 2020 the 10th International Conference on Communication and Network Security （ICCNS 2020）.Tokyo：ICCNS， 2020： 70-82.

［22］ RAMOS A， LAZAR M， FILHO R， et al. Model-based quantita-tive network security metrics： A survey ［J］. IEEE Communic-ations Surveys and Tutorials， 2017， 19（4）： 2704-2734.