基于理性思維培養的初中數學教學策略研究

［ 摘 要 ］數學是一門要求學習者具有極強思維性的學科，想讓學生學好數學就離不開對學生理性思維的培養.教學中，教師要改變傳統的教學模式，為學生搭建一個自主探究和合作交流的平臺，讓學生經歷觀察、猜想、交流、歸納等過程，逐步發展理性思維，進而提高數學能力與數學素養.

［ 關鍵詞 ］理性思維；自主探究；能力與素養

理性思維是一種思維品質，是數學學習的重要形式.數學在形成人的理性思維、科學精神和促進個人智力發展的過程中發揮著不可替代的作用.不過受唯分論的影響，部分教師的教學存在淺化、僵化、窄化等現象，“滿堂灌”的課堂教學模式依然存在，學生習慣于接受，學習中常常出現“知其然而不知其所以然”的現象，影響學習效果，限制學生理性思維的發展 . 在日常教學中，教師切勿通過強灌的方式將知識教給學生，而應預留時間讓學生去思考，引導學生養成追問“為什么”的品質和習慣，幫助學生厘清問題的來龍去脈，從而使學生的思維走向有序、深刻.下面，筆者結合教學實踐，談談培養學生理性思維的幾點認識.

追本溯源，執果索因

受“分數至上”價值觀的影響，教學中為了追求成績，部分教師常常直接將知識告知學生，然后布置大量的練習，以期通過“多練”加深知識理解，積累解題經驗，提高解題技能 . 殊不知這樣只追求“結果”的教學使得學生在解題過程中容易生搬硬套，不僅影響解題效果和解題信心，而且影響學生理性思維能力的發展.為了扭轉這一局面，教師應重視引導學生追本溯源，讓學生既知道知識從哪兒來，又知道知識去哪里，弄清數學知識的本源、本質，提高理性分析和解決問題的能力.

例如，在教學“全等三角形”一課時，教師啟發并指導學6997cdfcb1f8fb87560a46aad514b827生通過動手操作自主探索全等條件.在研究兩邊和一角時，學生提出這樣一個猜想：若兩個三角形的兩條邊對應相等，且其中一條邊所對的角也相等，那么這兩個三角形全等.面對學生的猜想，教師沒有直接評價，而是引導學生實踐探究.教學片段如下：

師：請大家按照如下步驟作三角形，然后說說你的發現.（教師用PPT展示操作步驟）

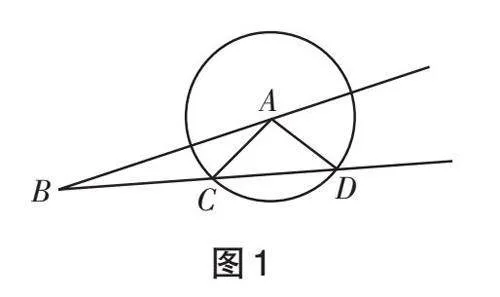
步 驟 如 下 ：（1） 畫 ∠ABC ；（2） 在角的一邊截取線段 AB ，在角的另一邊取點 C，然后以點 A 為圓心， AC 長為半徑畫圓；（3） 延長BC 邊，其與 ⊙A 的另一個交點為 D ，連接 AD .

學生積極操作，很快得到了圖1所示的圖形.

生 1： 在 △ABC 和 △ABD 中 ，AB=AB ， AC = AD ， ∠ABC=∠ABD ，這里雖然兩邊對應相等，且其中一邊所對的角也相等，但是這兩個三角形并不全等，也就是說剛剛的猜想不成立.

師：非常棒，我們在學習過程中會遇到許多神似或形似的知識內容，要加以辨析，切勿盲目套用.

師：增加一個怎樣的條件，可以使剛剛的猜想成立呢？

教師鼓勵學生以小組為單位，結合尺規作圖的經驗繼續探索.學生通過操作、交流，發現若兩個三角形為同一類型的三角形，那么滿足以上條件的兩個三角形全等.

學生通過以上探究活動，不僅激發了參與課堂的積極性，而且順利地證明了猜想，形成了正確深刻的認識.另外，為了讓學生的思維走向縱深，在此基礎上，教師繼續追問：增加一個怎樣的條件，可以使剛剛的猜想成立？通過多角度、全方位的思考與探究，可以有效激活學生的數學思維，使學生對兩個三角形全等的理解走向深刻、理性，從而在深化知識理解的同時，培養學生的理性思維，提高學生的自主探究能力.

問題驅動，思辨明理

數學是一門非常嚴謹的學科，在分析和解決問題的過程中要做到言之有理，論證有據.推理是理性思維的重要表現形式，其貫穿數學教學的始終.在日常教學中，教師要重視引導學生經歷公式的推理過程，從而幫助學生建構一條有序的思維鏈條，提高學生分析和解決問題的能力.

例如，學習“多邊形的內角和”時，若直接給出公式，然后套用，學生確實可以順利地解決問題，但是沒有經歷自主探究的過程，學生難以形成深刻的認識，很容易遺忘.另外，公式推導過程中蘊含豐富的數學思想方法，是培養學生思維能力，發展學生理性思維的重要素材.教師應重視引導學生經歷公式推導的全過程，從而在推導、講解的過程中提高學生的綜合學力.學生在學習本課內容前已經學習了三角形的內角和，并具有一定的圖形分割經驗.對此，教師可以學生為主，讓學生通過經歷從“特殊”到“一般”的探究，歸納總結出多邊形的內角和.為了便于探究，教師設計了如下“任務鏈”，讓學生在任務的驅動下，合理運用轉化思想解決問題 . 任務如下：

任務 1：你想運用什么思想方法來研究？

任務 2：還可以應用哪些方法來研究？

任務給出后，學生開始獨立思考，結合已有知識經驗，學生最容易想到通過分割法來探索多邊形的內角和.從實際反饋來看，學生大多采用分割法，但是所選取的分割方式有所不同，如有的學生從頂點出發，依次連接不相鄰的頂點；有的學生在多邊形內部任意找一點，連接各個點；也有學生在多邊形的邊上任意取一點，連接各個頂點；還有學生從多邊形外部任取一點，連接各個頂點.教學中，教師先引導學生從第一種方法入手，即取多邊形任意一個頂點，連接不相鄰的頂點，并讓學生思考以下問題：

問題 1：四邊形可以分割成幾個三角形？五邊形可以分割成幾個三角形？ n 邊形呢？

問題 2：一共分割了幾次？是否生成新的內角？

問 題 3： n 邊 形 的 內 角 和 與（ n - 1 ） 邊形的內角和有著怎樣的聯系？

問題4： n 邊形的內角和與三角形的內角和有著怎樣的聯系？

學生在問題驅動下得到結論： n邊形內角和為 （n - 2） × 180° .在此基礎上，教師可以讓學生利用其他分割方法繼續探索如何推導 n 邊形內角和公式，以此啟發學生多角度、全方位探索問題，感悟不同方法間的關聯，從而促進知識的深化 . 可見，在日常教學中，教師應堅持以學生為中心，以問題為引領，促進學生深度思考，從而培育學生的理性思維，提升學生的數學核心素養.由點及線，理性思考

學生理性思維能力是在學習過程中逐漸養成的，具有聯系性、生長性.教學中，教師要引導學生從聯系的視角出發，幫助學生打通從已知通往未知的思維通道，從而讓學生的“學”從局部走向整體，從膚淺走向深刻，逐步提高數學應用能力，發展理性思維.例如，“數格點算面積”教學中，教師從生活實際出發，創設如下問題情境：甲、乙兩人分別選取一塊空地栽樹，甲認為乙的土地面積大，理由是：自己地的一圈只栽15 棵樹，而乙的地一圈栽了 17 棵樹.而乙有不同的意見，他認為甲的面積更大，理由是：自己地的內部只能栽16棵樹，而甲的地可以栽17棵樹.你知道他倆誰的地面積更大？

（假設所栽樹的水平、垂直間距相等）

設計意圖 借助實際問題讓學生體會研究不規則圖形面積的重要性，有效激發學生的探究欲.

為了便于學生發現其中的規律，教師設計了如下活動：（格點多邊形的面積為 S ，多邊形內部的格點數為 N ，多邊形邊上的格點數為 L ，小正方形邊長為1）

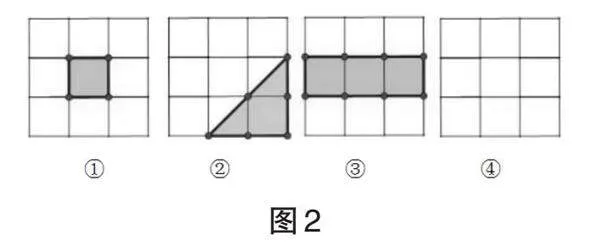
活動一：（1）如圖2，其中①②③均是 N = 0 的格點多邊形，請在④中再畫一個 N = 0 的格點多邊形.

（2）根據圖2，完成表1：

（3） 結合表 1，思考 S ， L 之間的關系.

活動二：結合活動一的經驗，請分別畫出 N = 1 ， 2 ， 3 ，…的格點多邊形，探究 S ， L ， N 三者之間的關系.

教師讓學生從簡單圖形入手，通過操作、觀察、猜想、歸納，最終得到 S ， L ， N 三者之間的關系，即 S =1/2L + N - 1 .通過由點及線的方式進行深入探索，有利于培養學生的理性思維.

總之，理性思維能力不是與生俱來的，需要通過后期的刻苦學習.在教學中，教師應致力于學生理性思維的培養，結合學生實際開展一定的探究活動，有效激活學生的理性思維，從而讓學生的思維從膚淺走向深刻，有效提高學生分析和解決問題的能力，發展學生的數學核心素養.