超邊內部結構對無標度超網絡魯棒性的影響

摘要： 鑒于現有超網絡魯棒性的研究中并未考慮超邊內部結構對超網絡魯棒性的影響，提出一種能描述超邊內部結構與超網絡魯棒性關系的容量負載模型，并通過仿真實驗獲得了超邊內節點在優先連接、隨機連接、全連接3種方式下，k均勻無標度超網絡的魯棒性。通過對比分析發現，無標度超網絡的魯棒性與其超邊內節點的連接方式密切相關，同時也與超邊內節點的規模k以及超邊內部普通邊的數量mk有關。研究結果表明，超邊內部結構對無標度超網絡整體的魯棒性有較大的影響。

關鍵詞： 無標度超網絡；超邊內部結構；容量負載模型；級聯故障；魯棒性

中圖分類號： O157.5; N945.15文獻標識碼： A

Influence of Structure Inside Hyperedge on Robustness of Scale-free Hypernetwork

ZHOU Bin， MA Fuxiang GAO Shujie， MA Xiujuan LI Mingjie

（1.College of Computer， Qinghai Normal University， Xining 810016， China;

2.The State Key Laboratory of Tibetan Intelligent Information Processing and Application， Xining 810008， China）

Abstract：In the existing work on the robustness of the hypernetworks， researchers have not considered the effect of internal structure on the robustness of the hypernetworks. Aiming at this problem， this paper proposes a capacity-load model that can describe the relationship between the internal structure and the robustness of the hypernetworks. By simulation experiments， we obtain the robustness of the k-uniform scale-free hypernetwork under three modes： preferential connection， random connection， and completed connection within hyperedges. Analysis of the comparison experiments reveals that the robustness of the scale-free hypernetwork is related to the ways of nodes' connection， the size k of the nodes， and the number of ordinary edges mk within the hyperedges.The results show that the internal structure of the hyperedges has a large impact on the overall robustness of the scale-free hypernetworks.

Keywords： scale-free hypernetwork; internal structure of hyperedge; capacity-load model; cascading failures; robustness

0 引 言

隨著信息技術的發展，復雜網絡已經成為建模各類復雜系統的有效工具，例如電力網絡[1]、通信網絡[2]、交通網絡[3]和金融網絡[4]等。建模復雜系統的最終目標是分析系統的性能，并達到改善系統性能的目的。對很多現實復雜系統來說，魯棒性是其最重要、最基本的系統性能之一。近年來，研究者也依據復雜網絡理論成功研究了各種復雜系統的魯棒性，獲得了很多重要的結論，并提出了眾多行之有效的優化系統魯棒性的策略[57]。

但隨著人類社會的不斷發展，與人類生活息息相關的各類系統也越來越復雜。國內外多位學者[810]提出很多現有的系統已不能單純地抽象為任意兩個節點之間的關系，而是多個節點間存在更加復雜的聯系。因此，基于圖的復雜網絡理論已不能完全表示日益復雜的系統結構[1113]，也無法深刻分析這類復雜系統的性能。超網絡理論的出現，為研究這類復雜系統帶來了新的思路和研究方法。超網絡中的超邊可以更好地表示多個節點間同時存在的某種復雜關系，因此近年來，超網絡被用于建模許多真實復雜系統，且表現出了比復雜網絡更好的優越性[1416]。雖然超網絡的建模研究已日趨成熟，但由于超網絡結構的復雜性，目前對超網絡動力學性質的研究還處在起步階段。同時，已有的研究結果也表明，超網絡確實表現出了和普通復雜網絡不同的動力學性質。例如，Wu等[17]將復雜系統的同步首次引入到超網絡中，發現超網絡相較于普通網絡可以更恰當地描述多方面的耦合協作關系，更有利于同步問題的研究。Gong等[18]構建了在線社交超網絡，解決了普通社交網絡不能準確描述社交網絡中群聚特性的問題，并對在線社交超網絡中信息全局傳播的動態過程進行了仿真分析，發現同復雜網絡結構相比，基于超圖結構的超網絡中信息全局傳播速度更快，波及范圍更廣。Ma等[19]通過對比研究發現，雖然超網絡面對外部攻擊表現出了和普通網絡類似的性質，但超網絡的級聯故障過程卻比普通的復雜網絡緩慢，面對同樣的外部擾動，表現出了比普通網絡更強的魯棒性。Ma等[20]同樣根據超網絡的結構提出了一類可以描述超網絡級聯故障過程的級聯故障模型，通過該模型的仿真分析，也獲得了類似的結論。此外，Chen等[21]提出了基于超邊擴散的容量負載級聯故障模型，將模型分別應用在隨機超網絡和小世界超網絡上，對比發現兩類超網絡相較于普通網絡具有更強的魯棒性，且隨機超網絡比小世界超網絡具有更強的魯棒性。Luo等[22]發現超網絡相較于普通網絡更適合用于表示復雜的城市公交網絡，節點為公交站點，超邊為線路，并分析了該超網絡的魯棒性，發現公交超網絡對隨機攻擊魯棒，蓄意攻擊脆弱。但上述研究結果大多都默認超網絡超邊內節點的連接方式為全連接，然而現實超網絡中節點內部的連接方式往往都是非全連接的，例如在微信群超網絡，交通超網絡等。因此，以往的研究忽略了超邊的內部結構對超網絡魯棒性的影響，也即忽略了微觀結構對系統整體性能產生的作用。例如，在集成電路開發中，通過超網絡的思想去設計集成電路，研究集成功能塊內部電子元件間的連接關系，可以進一步優化集成電路的魯棒性；再比如，在快遞服務網的布局當中，通過布局快遞網內部的交互關系，從而對快遞服務網的結構進行優化，增強其魯棒性。因此，研究超邊內部結構對超網絡魯棒性的影響，將有利于更好地發現超網絡結構與超網絡魯棒性之間的關系，同時能更全面地認識和理解超網絡魯棒性的影響因素，從而能提出更好的優化策略，提高超網絡抵抗各類攻擊的能力，為進一步增強復雜系統的魯棒性提供可靠的理論支撐。

為此，本文以Barabasi-Albert （BA）無標度超網絡為基礎，考慮了超邊內節點的連接方式，構建了三類k均勻無標度超網絡，并基于Motter等提出的容量負載模型[23]的思想提出了一種新的容量負載模型，研究了超邊內部結構對超網絡魯棒性的影響。

1 超網絡與超網絡模型

超網絡是以超圖[2425]作為拓撲結構對復雜系統進行抽象后形成的網絡，超網絡通過超邊有效表達了多個節點同時滿足的某種關系，比普通網絡更加直觀。例如，作者合作超網絡表達了多個作者合作同一篇論文的情況[15]；交通超網絡表達了多個交通站點被同一條交通線路經過的情況[22]。

超網絡中節點vi的超度定義為包含節點vi的超邊的個數，記為dH（vi）[26]。而節點vi的節點度與普通網絡類似，依然定義為節點vi所關聯的普通邊的個數，記為d（vi）[26]。節點vi在單獨一條超邊ei內的普通度記為kei（vi）。

為了更好地發現超網絡中超邊的內部結構對超網絡魯棒性的影響，本文參考了Hu等[27]提出的k均勻無標度超網絡的演化思想，構建了三類超邊內節點不同連接方式的無標度超網絡模型，如表1所示。三類超網絡模型的具體構建過程如下所述。

步驟1 分別構建節點總數為N，超邊總數為M的k均勻無標度超網絡；

步驟2 斷開超邊內節點間的原有連接。當超邊內的節點之間采用優先連接的方式時，轉1）執行；采用隨機連接方式時，轉2）執行；采用全連接方式時，轉3）執行；

1）超邊內部節點采用優先連接方式：

（1）初始化：設Vei表示超邊ei內的節點集合，超邊ei（1≤i≤M）內的k（1≤k≤N）個節點構成超邊ei的導出子圖G（ei）中的孤立節點；選定3個節點進行全連接使其成為超邊內初始的連通分支C0；設Γt表示t時刻超邊內連通分支Ct的節點集合；

（2）增長：t+1時刻隨機選擇連通分支Ct外的一個節點vk（vk∈Vei，vkCt），增加到Ct中，構成新的連通分支Ct+1；vk加入連通分支時，以（3）中的方式選擇連通分支Ct內的一個節點vi（vi∈Vei，vi∈Ct）；重復（2），不斷增大連通分支，直至其包含超邊ei內的所有節點；

（3）優先連接：設kei，Ct（vi）表示超邊ei內的節點vi在連通分支Ct中的普通度。連通分支Ct外的節點vk選擇連通分支內的δm個節點并用普通邊進行連接；連通分支內的節點vi以優先連接概率Πi被選擇。

Πi=kei（vi）∑Γtj=1kei（vj），vi，vj∈Ct（1）

2）超邊內部節點采用隨機連接方式：

（1）初始化：使超邊ei（1≤i≤M）內的k（1≤k≤N）個節點成為超邊ei的導出子圖G（ei）中的孤立節點，然后給定節點重連邊的概率p∈［0，1］；

（2）超邊內節點以如下的方式隨機重連：a.生成一個隨機數r；b.隨機選擇同一超邊內的一對節點；c.如果r<p，判斷 b 中所選擇的節點對之間是否有連邊，若無連邊，則用一條普通邊連接，否則不做任何操作；

（3）重復步驟（2），直至生成p×k（k-1）/2條普通邊。

3）超邊內部節點全連接方式：

（1）初始化：使超邊ei（1≤i≤M）內的k（1≤k≤N）個節點成為超邊ei的導出子圖G（ei）中的孤立節點；

（2）超邊內節點重連：使k個節點中每對不同的節點之間都恰有一條邊相連，生成包含k個節點、k（k-1）/2條邊的全連通子圖；

步驟3 重復步驟2，直至遍歷超網絡中的所有超邊。

2 基于超邊內部結構的超網絡容量負載級聯故障模型

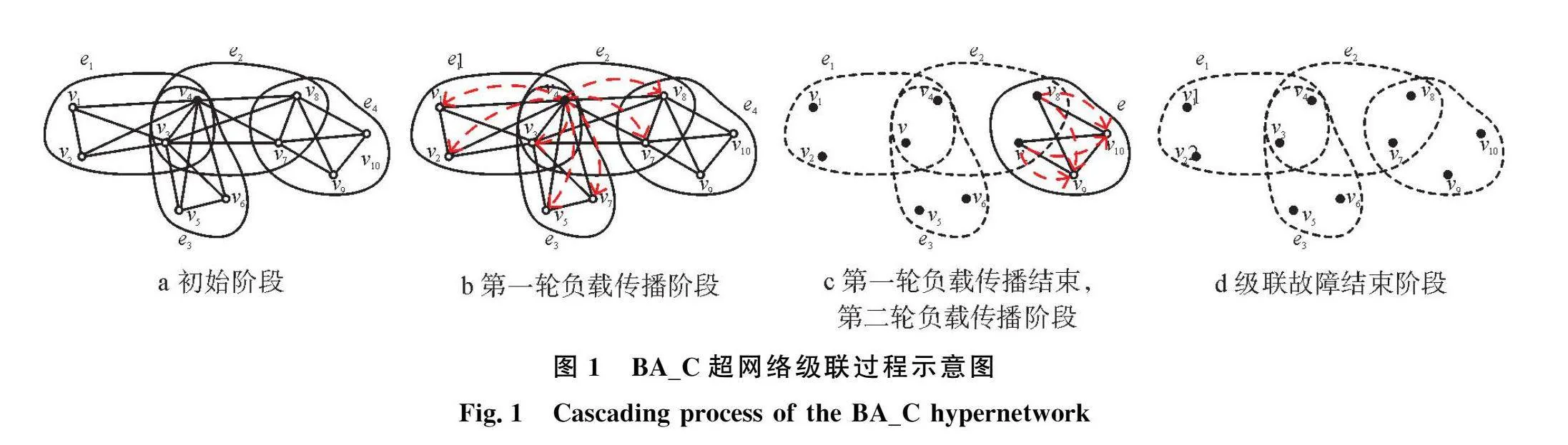
以BA_C超網絡為例，當超網絡中一個節點發生崩潰后，會將自身的負載分配到其未失效的鄰居節點，整個超網絡的級聯故障進程如圖1所示。圖1a中節點v4（填充狀態為失效節點，否則為正常節點）是初始時刻受到攻擊而失效的節點，其余為正常節點；圖1b中顯示初始攻擊節點v4失效后，向其鄰居節點分配負載（箭頭表示為失效節點負載傳播的方向）；圖1c中顯示第一輪負載分配結束后，節點的失效情況。此時超邊e e2和e3中的所有節點均已失效，則這三條超邊失效（虛線表示超邊失效，實線表示超邊未失效），負載通過節點v7和v8繼續向未失效的超邊e4傳播；圖1d表示所有超邊均已失效，級聯故障的擴散到此結束。

以往研究者提出的超網絡級聯故障模型，存在考慮指標過于單一的問題，以Chen等[21]提出的基于超邊擴散的超網絡級聯故障模型為例，作者將超網絡轉換成線圖進行研究，默認超邊內部節點全連接，當一條超邊受到攻擊失效時，負載會傳播到與其相鄰的未失效超邊上，并沒有考慮負載在超邊內部通過節點傳播的情況。為更好地描述超邊內部結構對超網絡魯棒性的影響，本文提出了一種新的容量負載模型用于分析超邊內部結構與超網絡魯棒性之間的關系。

在一個有N個節點的超網絡中，節點vi的初始負載與該節點的超度dH（vi）和節點度d（vi）有關，其初始負載Lvi（0）被定義為

Lvi（0）=α（dH（vi）+d（vi））β i=，…，N，α≥ β≥1（2）

為了控制節點vi的初始負載，設α為負載參數，β為可調參數。由式（2）可知節點初始負載與其節點超度和節點度成正比。

設節點vi與節點vj在某條超邊內通過普通邊連接。在t時刻，當節點vi因故障失效時，首先其負載Lvi將按照失效節點vi的超度dH（vi）等分，并將等分后的負載分配給與其關聯的所有未失效超邊，則與vi關聯的所有未失效超邊接收到的負載都為Lvi/dH（vi）。然后將某條超邊ei接收到的負載按照節點vi在超邊ei中的節點度kei（vi）等分，則節點vj接收到的負載如式（3）所示。

ΔLvi→vjt=Lvit×1dθHvi×1kθeivi（3）

其中，θ為擾動參數，且0≤θ≤1。由式（3）可以看出，t時刻超邊ei內的節點vj接收到的額外載荷ΔLvi→vj（t）與t時刻失效節點vi的超度、節點vi在超邊ei內的普通度以及節點vi的初始負載有關。若t時刻節點vj未失效，則其負載為節點vj在t-1時刻的負載加上從失效節點vi重分配到的負載，即：

Lvj（t）=Lvj（t-1）+ΔLvi→vj（t）（4）

在現實超網絡中，容量是節點或者超邊所能處理負載的最大值，與節點的初始負載成正比。設節點vj的容量為Cvj，如式（5）所示。

Cvj=（1+T）Lvj T≥0（5）

其中，T為容量參數，T的值越大，節點的容量就越大，抵御故障的能力就越強，但抵御成本會增加。臨界閾值TC是避免超網絡發生全局崩潰的最小容量值。當T>TC時，整個超網絡不會出現全局崩潰。當T<TC時，整個超網絡會發生全局崩潰。因此，T的臨界閾值TC是衡量超網絡魯棒性的重要指標。顯然，TC越小，表明超網絡越魯棒。

如果節點vj在獲得額外載荷之后發生失效，則其應滿足不等式：

Lvj（t-1）+ΔLvi→vj（t）>Cvj（6）

如果式（6）成立，則節點vj將過載失效，當vj的負載被重新分配后，可能會導致其它的節點發生失效。結合式（3），式（6）可以表示為

Lvj（t-1）+Lvi（t）×1dθH（vi）×1kθei（vi）>Cvj（7）

為了衡量超網絡的魯棒性，初始攻擊節點vi并使其失效，然后對它的負載進行重新分配。對于負載重新分配后的其它節點，若滿足式（7），則該節點失效。當超邊內節點全失效后，則此條超邊發生失效。當超網絡中的失效節點數達到一個穩定狀態或者所有節點全部失效（全局崩潰）后，統計超網絡中的失效超邊數FM（0≤FM≤M），計算超邊失效比例fM如式（8）所示：

fM=FMM，0≤fM≤1（8）

其中，M為超網絡的超邊總數，由式（8）可知，fM越大說明超網絡中失效超邊數越多，即超網絡的魯棒性越差。

3 仿真分析

在分析k均勻無標度超網絡超邊內部結構對超網絡魯棒性的影響時，本文以k均勻無標度超網絡為底層網絡構建了三類超網絡：BA_P超網絡、BA_R超網絡和BA_C超網絡，對三類無標度超網絡在蓄意攻擊和隨機攻擊兩種策略下的級聯故障進程進行仿真模擬，并記錄了相關實驗數據。仿真實驗中的隨機攻擊方式為隨機選取超網絡中的一個節點進行攻擊；而蓄意攻擊則是選取超網絡中最重要的節點進行攻擊，因為本文研究的是超網絡，所以在選擇節點重點性指標時，選取了能體現超邊內與超邊間結構共同作用的指標，即選擇超網絡中滿足節點度值與節點超度之和最大的節點進行攻擊。

3.1 參數敏感性分析

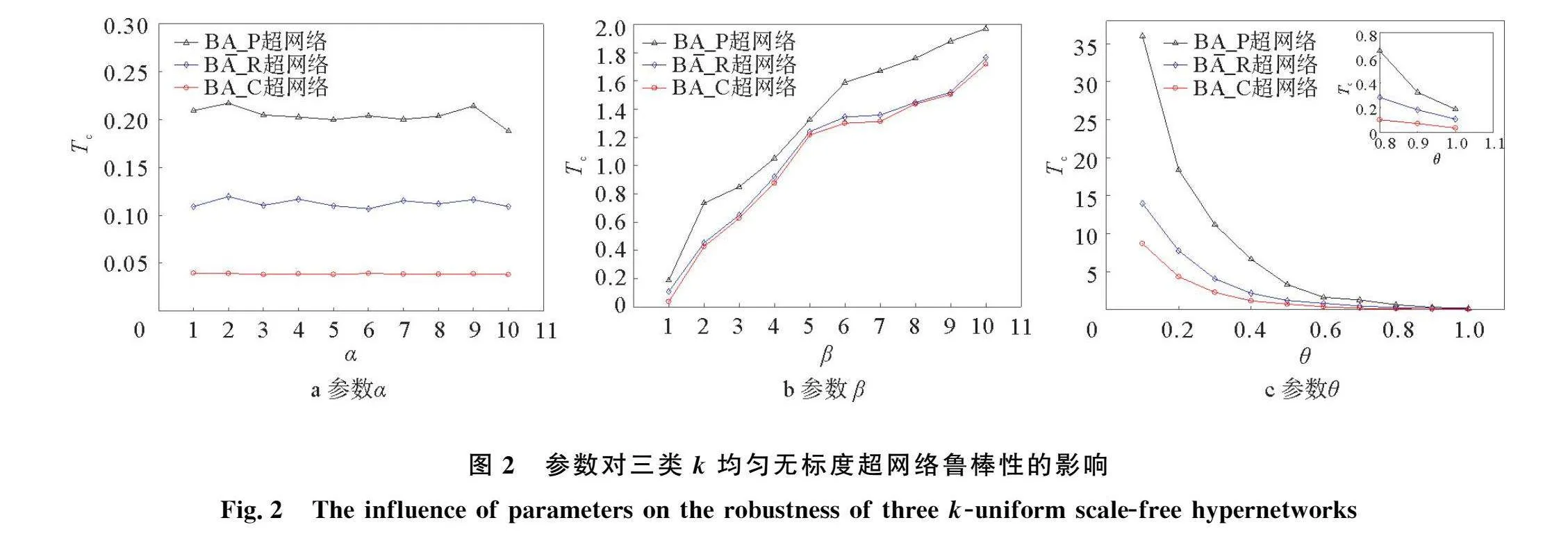
每類超網絡的規模與參數k相關，因此為了進行不同規模下的仿真分析，本文分別采用k為20， 40和60三種規模的網絡。本文研究的重點在于發現超邊內部結構對超網絡魯棒性的影響，為了消除其他不確定因素對魯棒性的影響，這里本文做了參數敏感性分析，如圖2所示。從圖2a中可以看出，三類超網絡對參數α的敏感性較弱，不論α的值如何增大，三類超網絡的魯棒性臨界閾值TC始終保持在一個相對穩定的狀態。α值為10時，三類超網絡魯棒性最優；由圖2b中可知，三類超網絡對參數β的敏感性大致相同，且魯棒性臨界閾值TC與參數β成正比例關系，也即魯棒性會隨著參數β的增大而變差。β值為1時，三類超網絡魯棒性最優；由圖2c可以發現，三類超網絡對參數θ的敏感性較強，其中參數θ對BA_P超網絡的影響尤為明顯。三類超網絡的魯棒性臨界閾值TC與參數θ成反比例關系，即魯棒性隨著參數θ的增大而變強。θ值為1時，三類超網絡魯棒性最優。

因此在仿真分析當中使用控制變量法，選取使得三類超網絡魯棒性達到最優時的參數值，即負載參數α取值為10，參數β取值為1，擾動參數θ取值為1，為了保證結果的有效性與真實性，實驗結果取50次結果的平均值。

3.2 三類k均勻BA無標度超網絡魯棒性分析

圖3顯示了在不同超網絡規模下，三類k均勻無標度超網絡在受到攻擊時，其超邊失效比例fM隨容量參數T的變化情況。圖中結果表明：在蓄意攻擊和隨機攻擊兩種策略下，超邊失效比例隨容量參數值的增大呈遞減趨勢，并在一定的容量參數下達到全局崩潰的臨界閾值。當T≤TC時，三類k均勻無標度超網絡均處于全局崩潰的狀態，當T>TC時，故障規模開始減小并最終達到全局不失效的狀態。

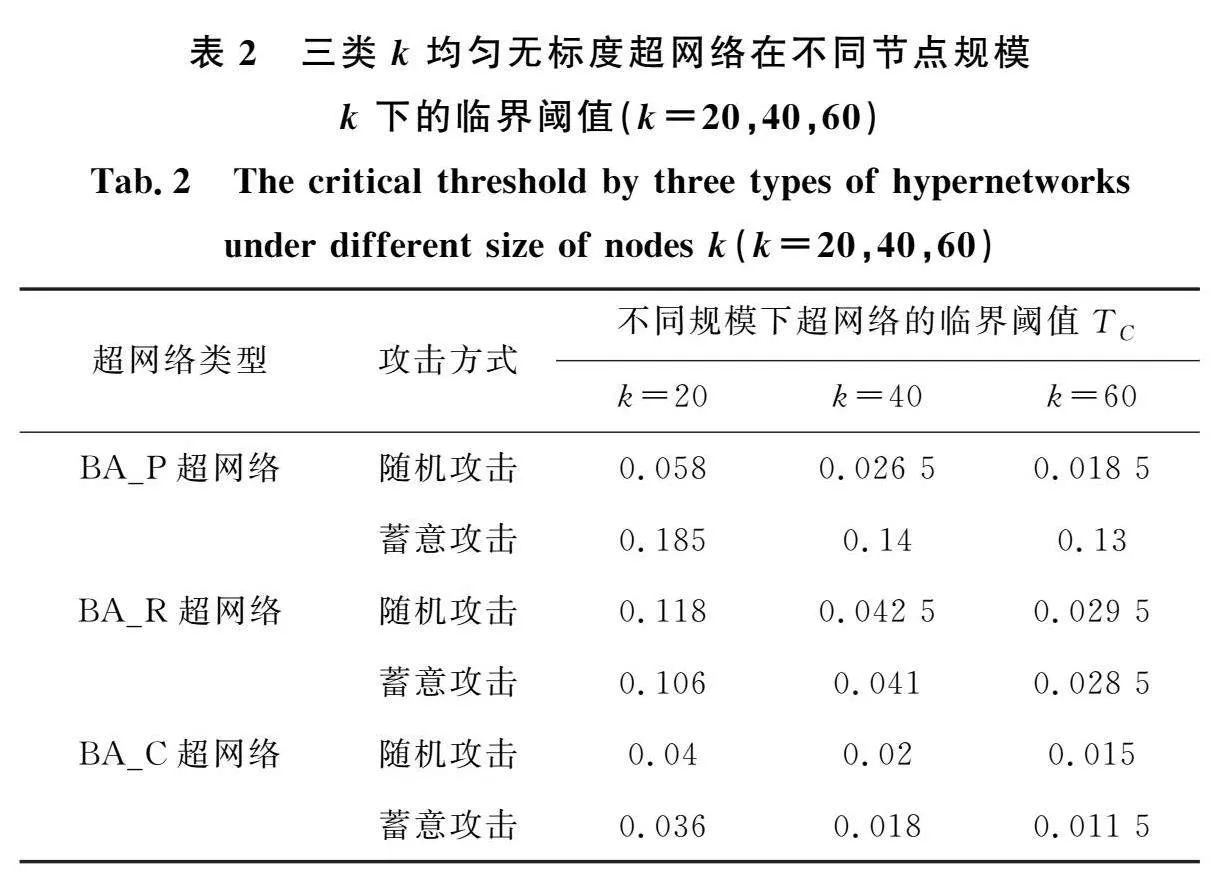
當k=20時，k均勻BA_P超網絡，在蓄意攻擊方式下，當容量參數T=0.185，超網絡的崩潰比例fM=1，即此時超網絡發生全局崩潰；當容量參數T>0.185時，超網絡的崩潰比例fM<1，因此超網絡在受到蓄意攻擊時其臨界閾值TC=0.185；同理分析可得，k均勻BA_P超網絡在受到隨機攻擊時其臨界閾值TC=0.058。由于TC越小，魯棒性越強，結合表2的結果可以明顯看出，k均勻BA_P超網絡在隨機攻擊下魯棒，在蓄意攻擊下脆弱。同理分析可得，k均勻BA_R超網絡在蓄意攻擊下魯棒，在隨機攻擊下脆弱；k均勻BA_C超網絡在蓄意攻擊下魯棒，在隨機攻擊下脆弱。

此外從圖3中可以明顯看出，隨著三類k均勻無標度超網絡規模的增大，其臨界閾值TC均呈逐漸變小的趨勢。這是因為隨著節點規模的增大，當超網絡中的節點發生故障后，失效節點負載重分配時就會有更多的鄰居節點分擔其負載，使超網絡更不容易崩潰。因此，k均勻無標度超網絡的規模越大，超網絡在受到攻擊時越魯棒。

以往的研究結果表明[1921]，當忽略超邊內節點的連接方式時，k均勻無標度超網絡在遭受外部攻擊時與普通的無標度網絡類似，即表現出對隨機攻擊魯棒，對蓄意攻擊脆弱的特性。但本文分析發現，當k均勻無標度超網絡超邊內部節點的連接方式不同時，k均勻無標度超網絡表現出了不同的魯棒性，即當超網絡超邊內節點采用優先連接方式時，超網絡表現出了與已有研究結果一致的魯棒性，而當超邊內的節點采用其他兩種連接方式時，超網絡表現出了相反的魯棒性，但在兩種攻擊方式下的魯棒性差異不大，且超邊內節點的規模對其有重要的影響，即超邊內節點越多，則超邊內節點的連接方式產生的影響也越大。同時，本文對超邊內節點連接方式對魯棒性產生影響的原因進行了具體的分析。這里k均勻無標度超網絡的各超邊之間的連接方式為優先連接。

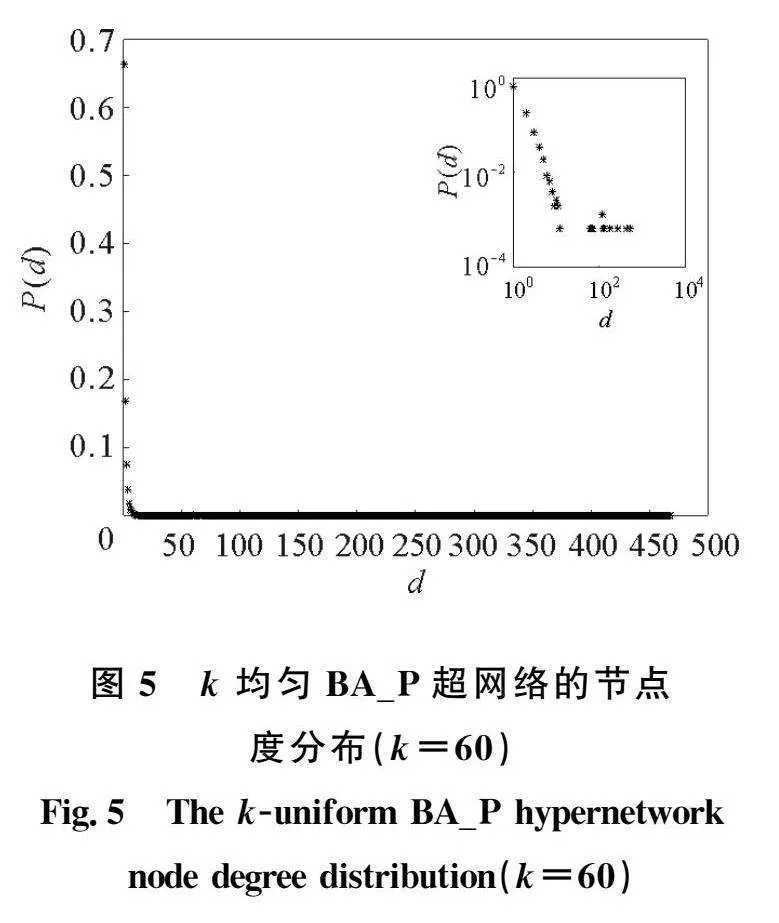
1）當超邊內部節點之間的連接方式為優先連接時，每條超邊內部的節點度分布與節點超度分布均為冪律分布，如圖4和圖5所示。這表明這種連接方式加強了超網絡的無標度特性，因此BA_P超網絡在受到攻擊時與無標度超網絡表現出一致的特性，即對隨機攻擊魯棒，對蓄意攻擊脆弱；

2）當超邊內部節點之間的連接方式為隨機連接時，每條超邊內部的節點度分布為泊松分布，又因節點的超度分布仍為冪律分布，所以BA_R超網絡整體的節點度分布在超度分布的影響下就會呈現偏態的泊松分布，如圖6所示。因此超邊內節點的隨機連接方式改變了超網絡整體的無標度特性，所以BA_R超網絡在受到攻擊時呈現出與ER隨機網絡相同的特性，即對隨機攻擊脆弱，對蓄意攻擊魯棒；

3）當超邊內部節點之間采用全連接的方式時，每條超邊內部為一個規則網絡，因為節點超度分布為冪律分布，如圖4所示，則當一個超度較大的節點遭受到攻擊時，介于本文所規定的負載傳播方式，如第2部分的式（3）所示，失效節點在進行負載傳播的過程中，當超度大的節點vi其負載傳播時，分配到其相鄰未失效節點vj所在超邊上的負載就會相對更少，為Lvit/d θHvi。又因超邊內部節點采用全連接的方式，那么失效節點vi的每個未失效的鄰居節點vj就會分到相對更少的負載，即Lvit/d θHvikθeivi。所以此時超網絡會表現出對蓄意攻擊魯棒，對隨機攻擊脆弱的特性。此外，Ma等[20]研究的無標度超網絡雖然也采用了超邊內全連接的方式，但其研究的k均勻無標度超網絡中k=3，也即超邊內節點的規模僅為3。因此，在Ma等的研究[20]中，超邊內節點的連接方式對超網絡魯棒性產生的影響非常小，不足以改變超網絡整體的魯棒性。本文研究發現，當k均勻無標度超網絡超邊內節點間全連接，且k≥8時，會對k均勻無標度超網絡的魯棒性產生重要的影響，甚至改變其原有的魯棒性，如圖7所示。

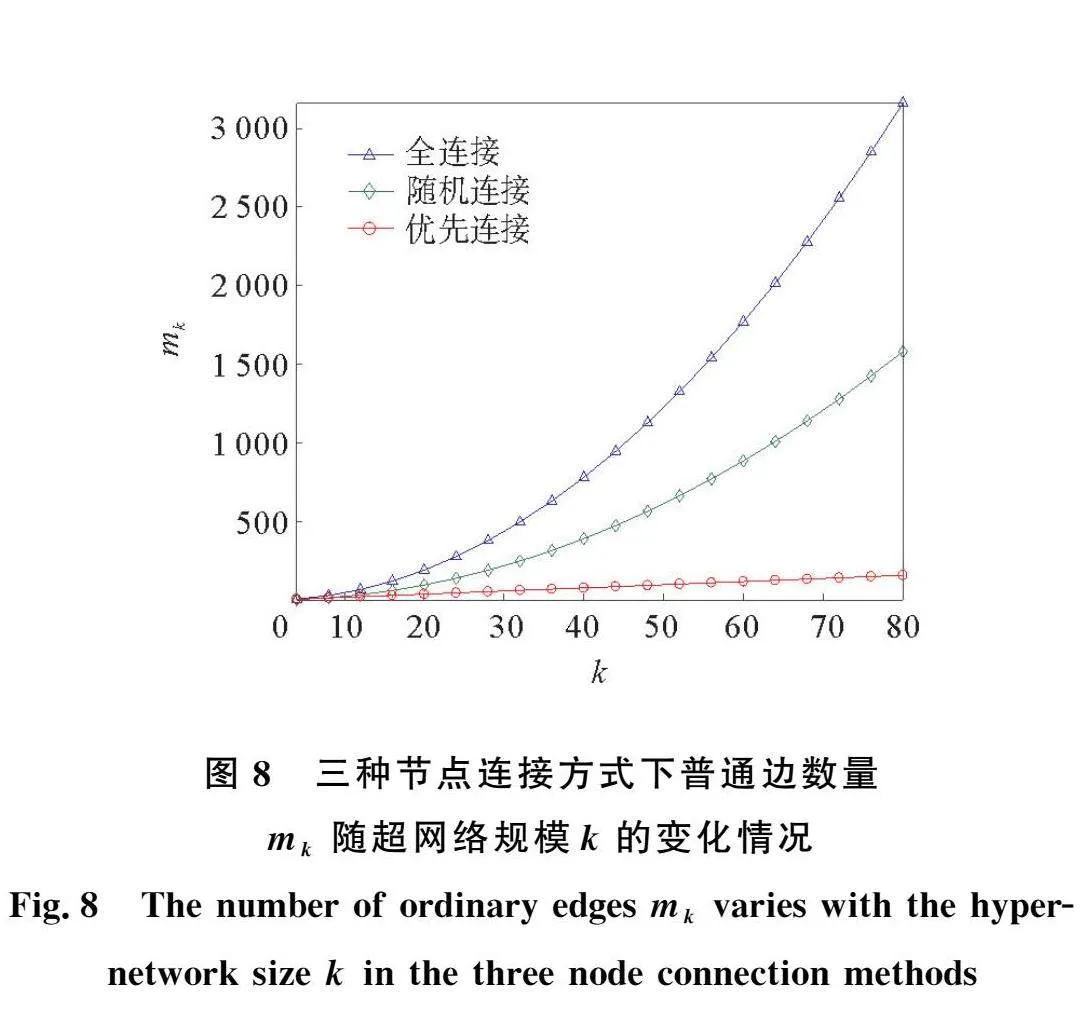
另外，結合表2中的數據分析得出，k均勻無標度超網絡在面對蓄意攻擊時，BA_C超網絡的魯棒性最好，其次是BA_R超網絡，最差的是BA_P超網絡；分析其原因為：k均勻無標度超網絡在面對蓄意攻擊時的魯棒性與超邊內部的普通邊數量mk有關。超邊內部不同結構的普通邊數量如圖8所示。因為在蓄意攻擊時，攻擊的是超邊內部超度占比與節點度占比之和最大的節點，普通邊越多，就會有更多的鄰居節點在負載傳播的過程中分擔其負載。所以在蓄意攻擊策略下，超邊內部普通邊的數量mk越大，k均勻無標度超網絡的魯棒性也越好。而k均勻無標度超網絡在面對隨機攻擊時，因隨機攻擊具有一定的隨機性，又因為無標度超網絡本身的無標度特性，從而減弱了超邊內部普通邊的數量對魯棒性的影響。

4 結論

為了突破現有超網絡結構魯棒性研究的局限性，探究超邊內部結構對超網絡魯棒性的影響，本文提出三類超邊內部結構不同的k均勻無標度超網絡模型，并提出一種新的容量負載模型分析了超邊內部結構對超網絡整體魯棒性的影響。得到結論：當超邊內節點的連接方式與超網絡各個超邊間的連接方式一致時，k均勻無標度超網絡對隨機攻擊魯棒，對蓄意攻擊脆弱；當超邊內節點的連接方式與超網絡各個超邊間的連接方式不一致時，k均勻無標度超網絡對隨機攻擊脆弱，對蓄意攻擊魯棒；當超邊內節點的規模k較大時，其連接方式對k均勻無標度超網絡魯棒性的影響也較大；當超邊內普通邊數量mk越大，k均勻無標度超網絡魯棒性越好。

本文的研究結果對進一步理解微觀結構對系統整體性能的影響有重要的意義，同時也為進一步優化超網絡的結構魯棒性提供了重要的參考。

參考文獻：

[1]REN H P， GAO Y， HUO L， et al. Frequency stability in modern power network from complex network viewpoint[J]. Physica A， 2020， 545（3）： 123558.

[2]WANG T， CHENG H， WANG X. A link addition method based on uniformity of node degree in interdependent power grids and communication networks[J]. Physica A， 2020， 560（5）： 125112.

[3]CAI W X， LIANG F F， WANG Y C， et al. An innovative approach for constructing a shipping index based on dynamic weighted complex networks[J]. Physica A， 202 578（5）： 126101.

[4]毛昌梅， 韓景倜， 劉舉勝. 基于復雜網絡的銀行波動溢出效應研究[J]. 復雜系統與復雜性科學， 2020， 17（2）： 1121.

MAO C M， HAN J T， LIU J S. Volatility spillover effect of chinese listed commercial banks based on complex network[J]. Complex Systems and Complexity Science， 2020， 17（2）： 1121.

[5]王哲， 李建華， 康東， 等. 復雜網絡魯棒性增強策略研究綜述[J]. 復雜系統與復雜性科學， 2020， 17（3）： 126+46.

WANG Z， LI J H， KANG D， et al. Review on strategies enhancing the robustness of complex network[J]. Complex Systems and Complexity Science， 2020， 17（3）： 126，46.

[6]WANG S L， L W Z， ZHANG J H， et al. Method of power network critical nodes identification and robustness enhancement based on a cooperative framework[J]. Reliability Engineering & System Safety， 202 207：107313.

[7]GAO J， BULDYREV S V， HAVLIN S， et al. Robustness of a network formed by n interdependent networks with a one-to-one correspondence of dependent nodes[J]. Physical Review E， 2012， 85（6）： 066134.

[8]陳關榮. 探索復雜網絡的高階拓撲及其應用[R]. 北京： 中國指揮與控制學會， 2021.

CHEN G R. Exploring higher-order topologies of complex networks and applications[R]. Beijing： Chinese Institute of Command and Control.

[9]FEDERICO B， GIULIA C， IACOPO I， et al. Networks beyond pairwise interactions： structure and dynamics[J]. Physics Reports， 2020， 874： 192.

[10] SINAN G A， CLIFF J， CARLOS O M， et al. Hypernetwork science via high-order hypergraph walks[J]. EPJ Data Science， 2020， 9（1）： 519535.

[11] WANG J W， RONG LL， DENG Q H， et al. Evolving hypernetwork model[J]. The European Physical Journal B， 2010， 77（4）： 493498.

[12] ESTRADA E， RODRGUEZ-VELZQUEZ J A. Subgraph centrality and clustering in complex hyper-networks[J]. Physica A， 2006， 364（3）： 581594.

[13] 索琪， 郭進利. 基于超圖的超網絡：結構及演化機制[J]. 系統工程理論與實踐， 2017， 37（3）： 720734.

SUO Q， GUO J L. The structure and dynamics of hypernetworks[J]. Systems Engineering-Theory & Practice， 2017， 37（3）： 720734.

[14] 李甍娜， 郭進利， 卞聞， 等. 網絡視角下的唐詩[J]. 復雜系統與復雜性科學， 2017， 14（4）： 6671.

LI M N， GUO J L， BIAN W， et al. Tang poetry from the perspective of network[J]. Complex Systems and Complexity Science， 2017， 14（4）： 6671.

[15] 胡楓， 趙海興， 何佳倍， 等. 基于超圖結構的科研合作網絡演化模型[J]. 物理學報， 2013， 62（19）： 547554.

HU F， ZHAO H X， HE J B， et al. An evolving model for hypergraph-structure-based scientific collaboration networks[J]. Acta Physica Sinica， 2013， 62（19）： 547554.

[16] 胡楓， 劉猛， 趙靜， 等. 蛋白復合物超網絡特性分析及應用[J]. 復雜系統與復雜性科學， 2018， 15（4）： 3138.

HU F， LIU M， ZHAO J， et al. Analysisand application of the topological properties of protein complex hypernetworks[J]. Complex Systems and Complexity Science， 2018， 15（4）： 3138.

[17] Wu Z Y， Duan J Q， Fu X C. Synchronization of an evolving complex hyper-network[J]. Applied Mathematical Modelling， 2014， 38（11/12）： 29612968.

[18] 鞏云超， 李發旭， 周麗娜， 等. 在線社交超網絡的信息全局傳播模型[J]. 電子科技大學學報， 202 50（3）： 437445.

GONG Y C， LI F X， ZHOU L N， et al. Global Dissemination of Information Based on Online Social Hypernetwork[J]. Journal of University of Electronic Science and Technology of China， 202 50（3）： 437445.

[19] 馬秀娟， 趙海興， 胡楓. 基于超圖的超網絡相繼故障分析[J]. 物理學報， 2016， 65（8）： 374383.

MA X J， ZHAO H X， HU F. Cascading failure analysis in hyper-network based on the hypergraph[J]. Acta Physica Sinica， 2016， 65（8）： 374383.

[20] MA X J， MA F X， YIN J， et al. Cascading failures of k uniform hyper-network based on the hyper adjacent matrix[J]. Physica A， 2018， 510： 281289.

[21] CHEN Y， MA X J， MA F X， et al. The capacity load model of k-uniform hyper-network based on equal load distribution[J]. Journal of Physics： Conference Series， 202 1828（1）： 012060.

[22] 羅海秀， 趙海興， 肖玉芝， 等. 基于超圖的公交超網絡拓撲特性及魯棒性分析[J]. 西南大學學報（自然科學版）， 202 43（10）： 181191.

LUO H X， ZHAO H X， XIAO Y Z. A hypergraph-based analysis of the topology and robustness of bus hypernetworks[J]. Journal of Southwest University （Natural Science Edition）， 202 43（10）： 181191.

[23] MOTTER A E， CHENG L Y. Cascade-based attacks on complex networks[J]. Physical Review E， 2002， 66（6）： 065102.

[24] BERGE C. Graphs and Hpergraphs[M]. New York： Elsevier， 1973.

[25] BERGE C， STERBOUL F. Equipartite colorings in graphs and hypergraphs[J]. Journal of Combinatorial Theory， Series B， 1977， 22（2）： 97113.

[26] BRETTO A. Hypergraph Theory[M]. Heidelberg： Springer， 2013.

[27] 胡楓， 趙海興， 馬秀娟. 一種超網絡演化模型構建及特性分析[J]. 中國科學： 物理學 力學 天文學， 2013， 43（1）： 1622.

HU F， ZHAO H X， MA X J. An evolving hypernetwork model and its properties[J]. Scientia Sinica（Physica， Mechanica& Astronomica）， 2013， 43（1）： 1622.

（責任編輯 李 進）