基于一個復混沌系統的圖像加密算法

摘要： 為改進基于低維系統設計的加密算法存在密鑰空間小等缺陷，構造了一個新的五維復混沌系統，利用相圖、平衡點、參數的影響、Lyapunov指數譜、分岔圖以及譜熵復雜度探究了其混沌動力學性質。研究發現復系統動力學行為豐富，較低維系統更適合應用于圖像加密算法。進而，基于此系統，提出了一個新的加密方案。該方案包括三次擴散及一次置亂，可以很好地增加圖像傳輸中的安全性。最后，通過計算密鑰空間、信息熵、相鄰像素相關性等對此加密方案進行性能分析。分析結果表明，所設計的加密方案具有較大的密鑰空間，擁有良好的加密效果和抵擋外部攻擊的能力。

關鍵詞： 復混沌系統；Zigzag變換；有限域理論；圖像加密

中圖分類號： TP309.7; O415.5文獻標識碼： A

Image Encryption Algorithm Based on a Complex Chaotic System

WANG Yue， AN Xinlei， SHI Qianqian， LIU Siyang

（School of Mathematics and Physics， Lanzhou Jiaotong University， Lanzhou 730070， China）

Abstract：In order to improve the small key space of the encryption algorithm based on low-dimensional system design， a new five-dimensional complex chaotic system is constructed， and its chaotic dynamics properties are studied by using phase diagram， equilibrium point， Lyapunov exponential spectrum， bifurcation diagram and spectral entropy complexity. It is found that the dynamic behavior of this system is rich， and it is more suitable for image encryption algorithm than low-dimensional system. Furthermore， based on this system， a new encryption scheme is proposed in this paper. The scheme includes three diffusion and one scrambling， which can increase the security of image transmission. Finally， the performance of the encryption scheme is analyzed by calculating key space， information entropy， correlation of adjacent pixels and so on. The analysis results show that the encryption scheme designed in this paper has a large key space， good encryption effect and the ability to resist external attacks.

Keywords： complex chaotic system; Zigzag transform; finite field theory; image encryption

0 引言

隨著信息技術的發展，越來越多的圖像進入網絡，威脅著人們的隱私與安全。與同為信息載體的文字不同，圖像具有數據量大、圖像信息相關性強等固有特性。因此，傳統的加密方法（如數據加密標準（DES）等）并不適用于圖像加密。而混沌理論的蓬勃發展，混沌映射與混沌系統因其初值敏感性以及不可預測性等特點逐漸進入大眾視野［1］。自Matthews R［2］首次將混沌理論與圖像加密算法相結合以來，混沌密碼學進入了快速發展時期，越來越多基于混沌系統的圖像加密算法被提出［37］。例如，文獻［6］將一個4維超混沌Lorenz系統結合傳統的RSA加密算法，從測試數據表明該算法可以有效提高密文的抗攻擊能力。文獻［7］將超Chen系統與有限域理論相結合，利用一次置亂和兩次擴散對明文圖像進行加密，實驗結果表明該算法具有較大的密鑰空間。

混沌系統的復雜性與加密算法的安全性息息相關，一般來說，系統越復雜，將其運用在圖像加密中的效果越好。因此，許多學者針對混沌系統做出了創新［812］。比如，劉等［8］提出一種基于量子隨機行走并涉及Lorenz和Rssler多維混沌的三維圖像加密算法，有效提高了圖像在傳輸過程中的安全性。安等［9］設計了一種電磁感應效應下的混合神經元模型，發現其具有復雜的模型結構和高非線性特點，進而應用于圖像加密使加密算法的復雜性顯著提高。Yang等［10］介紹了一個分數階混沌系統，經過數值仿真發現其動力學行為豐富，運用在圖像加密中可以有效增加算法的安全性。提高系統的維數是提高混沌系統復雜性的方法之一。目前許多研究均基于低維系統［1314］，其往往具有密鑰空間小等缺陷。而復混沌系統的復變量包括實部和虛部，是實系統變量的兩倍，進而增加了系統的復雜性，應用在圖像加密算法中效果更好［15］。

本文構造了一個新的五維超混沌系統，通過相圖等探究了這個系統的動力學行為，探究發現其具有復雜的動力學行為，應用在加密算法中效果較好。基于此發現，設計了一個圖像加密方案，此方案主要過程為“擴散—擴散—置亂—擴散”，然后獲得密文圖像。最后通過計算密鑰空間、像素直方圖等對此方案進行測試，測試結果表明：本文設計的加密方案可以有效隱藏明文圖像信息，并且具有良好的抵抗統計攻擊的能力。

1 復混沌系統

文獻［1］基于經典Lorenz系統設計了一個新的三維模型：

=－ax+6.7y+yz=－0.5xz+rx－by=0.8xy－cz+0.5yz（1）

其中，a，b，c，r為系統參數，當a=12.5，b=0.125，c=1.72，r=45時，系統（1）為混沌系統。

本文在系統（1）的基礎上得到一個新的系統，具體形式為

=－ax+6.7y+yz=－0.5xz+rx－by=0.4（y+x）－cz+0.5yz（2）

其中，x=u1+u2i，y=u3+u4i為復變量，z=u5為實變量。將系統（2）的實部和虛部分離，可得到其實數形式：

1=－au1+6.7u3+u3u52=－au2+6.7u4+u4u53=－0.5u1u5+ru1－bu34=－0.5u2u5+ru2－bu45=0.8u1u3+0.8u2u4－cu5+0.6u3u5（3）

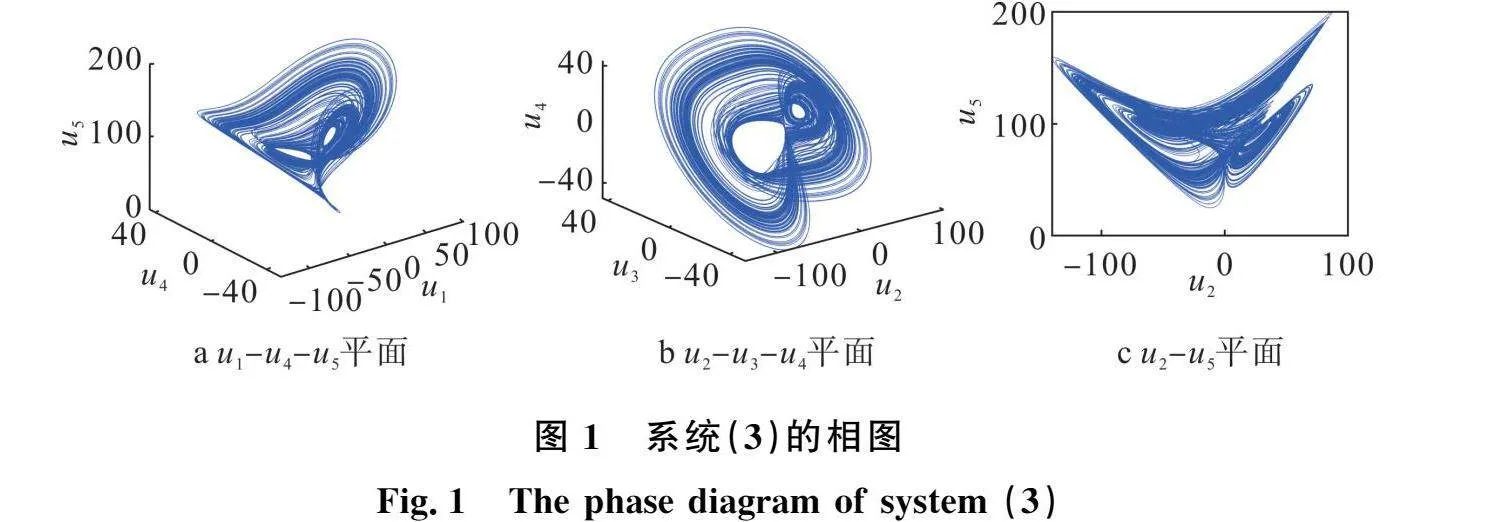
其中，u u2，u3，u4，u5為狀態變量，a，b，c，r為系統參數。當a=14，b=0. c=3.7，r=45時，系統（3）是混沌的。取初值為（ 1），經MATLAB仿真得到系統（3）的混沌吸引子，如圖1所示。此外，依據Wolf算法可以得到系統（3）在參數為a=14，b=0. c=3.7，r=45，初值為（ 1）下的Lyapunov指數分別為LE1=3.071 LE2=0.025 2，LE3=0.001 2，LE4=－10.086 LE5=－14.090 9。系統（3）有3個正Lyapunov指數，故系統為超混沌系統。超混沌系統的非線性動力學特性較普通系統的動力學特性復雜，運動軌跡多變，混沌序列的隨機性更強。進而，將系統（3）應用到圖像加密中，能夠有效提高加密算法安全性和圖像信息的保密性。

2 動力學分析

2.1 平衡點及其穩定性

令1=2=3=4=5=0，即

－au1+6.7u3+u3u5=0－au2+6.7u4+u4u5=0－0.5u1u5+ru1－bu3=0－0.5u2u5+ru2－bu4=00.8u1u3+0.8u2u4－cu5+0.6u3u5=0

取a=14，b=0. c=3.7，r=45，解得平衡點分別為S0=（0，0，0，0，0），S1=（0.015 4，0，7.427 4，0，－6.671 0），S2=（4.154 0，0，7.427 4，0，－6.671 0），S3=（－88.645 4，0，－12.837 7，0，89.971 0），S4=（32.413 5，0，4.694 2，0，89.971 0）。下面討論S0的穩定性。

在S0處將系統（3）線性化，得到Jacobian矩陣為

J（S0）=－a06.7000－a06.70r0－b000r0－b00000－c=－1406.7000－1406.70450－0.1000450－0.100000－3.7

則其特征方程為det（λI－J（S0））=（λ+3.7）（λ+14）（λ+0.1）－301.52=0。解得特征值分別為λ1=－3.700 0，λ2、3bLdMf35vCcd9zhma9bzYsA===11.653 0，λ4、5=－25.753 0。由λ2、3為正實數，λ λ4、5為負實數，得平衡點S0是一個不穩定的鞍點。同理可求得S S3，S4是不穩定的鞍焦點，S2是不穩定的鞍點［1］。

2.2 參數的影響

本節將運用數值方法探究參數b對系統（3）的影響。在固定參數a=14，c=3.7，r=45不變的前提下，分別令b=－8，b=－5，b=0.1，得到了1周期吸引子、２周期吸引子、混沌吸引子，如圖2所示，對應的時間序列圖如圖3所示［16］。從圖2與圖3中可以看出系統（3）既有周期態也有混沌狀態，具有豐富的動力學行為，應用在圖像加密算法中可以取得較好的加密效果。

2.3 分岔圖與Lyapunov指數譜

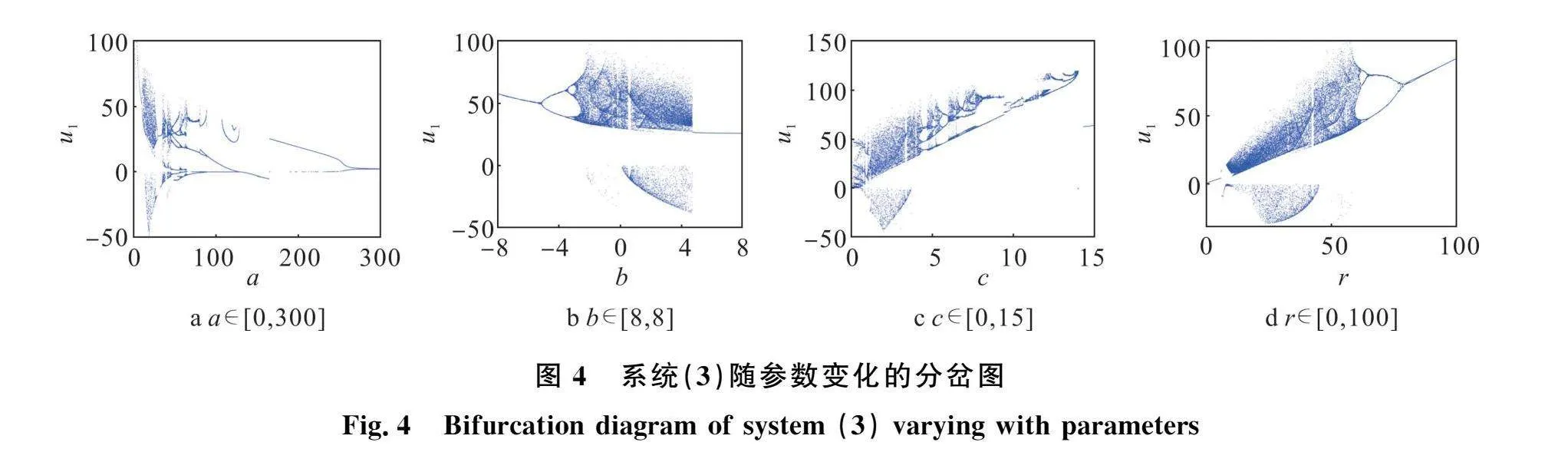
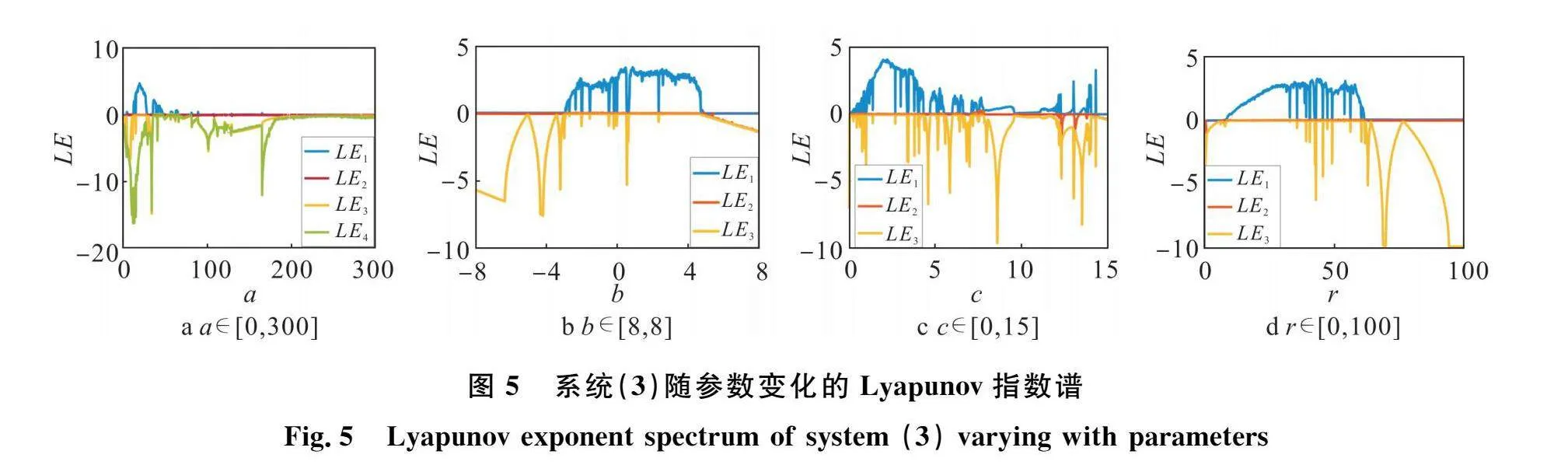
為進一步研究系統（3）的動力學行為，這一節將利用分岔圖與Lyapunov指數譜分析在參數不斷變化下，系統（3）的運動狀態。設置系統的初始條件不變，其它3個參數值固定，讓其中一個參數變化，得到相應的分岔圖和Lyapunov指數譜分別如圖4和圖5所示［3］。需要注意圖5a中兩個指數與圖5b～d中3個指數恒小于0故未展示。對比發現，分岔圖和Lyapunov指數譜的變化是一致的。從圖4與圖5中也可以看出系統（3）具有豐富的動力學行為。

2.4 譜熵復雜度

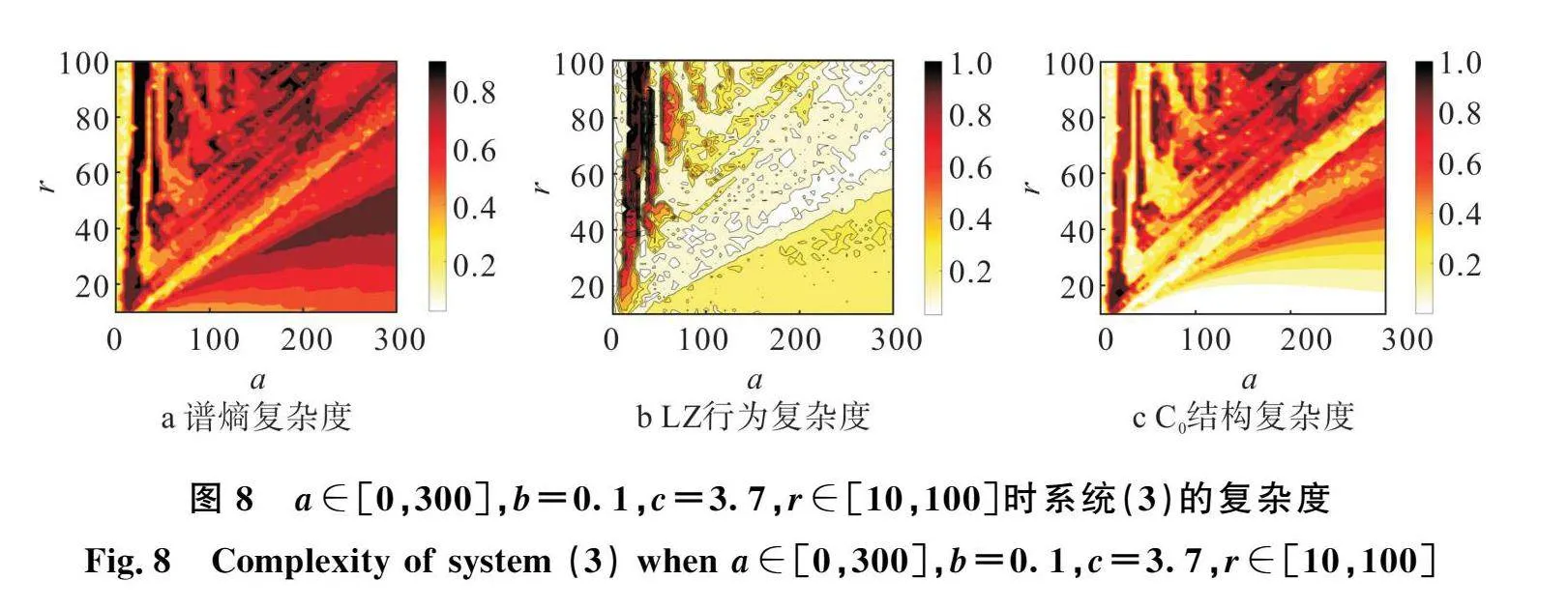
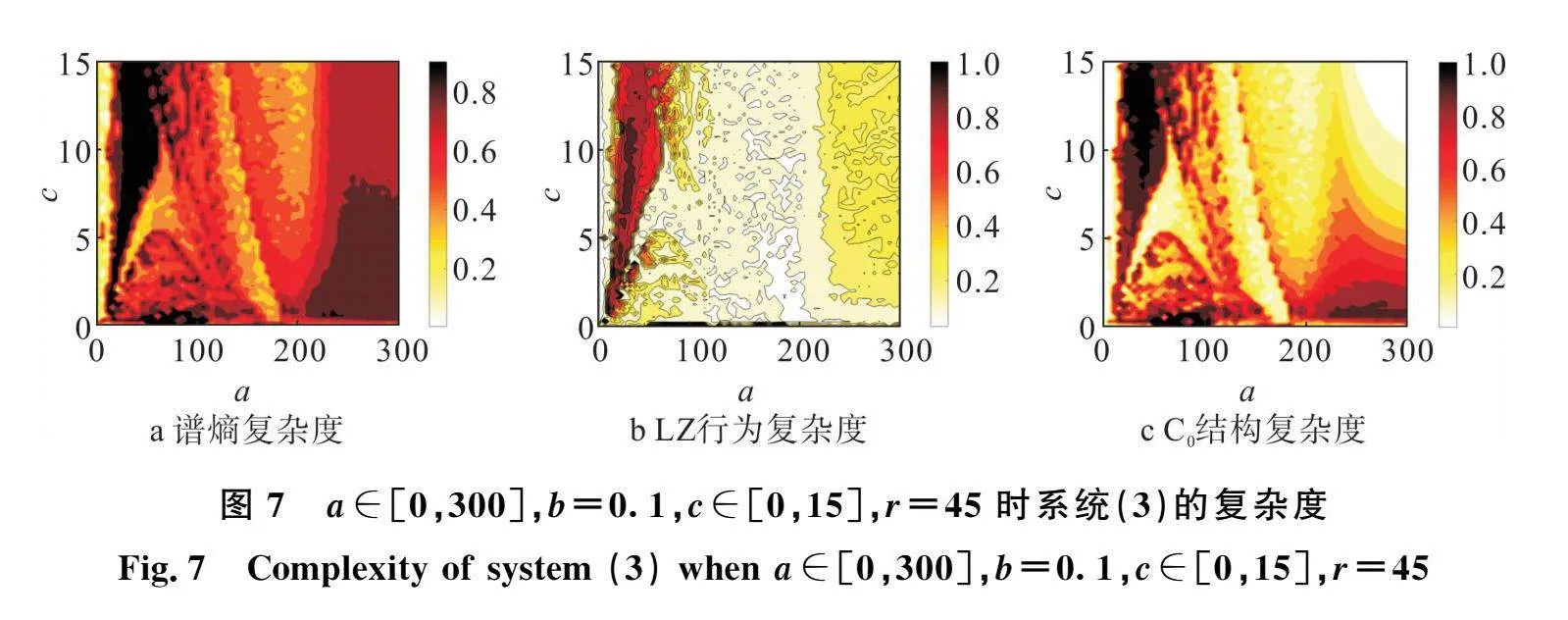
系統生成的序列與隨機序列的近似程度稱為復雜度，復雜度是評價非線性系統動態性能的重要手段。一般地，系統復雜度越大，生成的序列越接近隨機序列，意味著該系統應用在圖像加密中越安全。本文將分別以譜熵（Spectral Entropy， SE）、Lempl-Ziv（LZ）行為復雜度以及C0結構復雜度對系統（3）的復雜度進行分析。分別令a∈［0，300］，b∈［－8，8］，c=3.7，r=45、

a∈［0，300］，b=0. c∈［0，15］，r=45、a∈［0，300］，b=0. c=3.7，r∈［10，100］得到系統（3）的復雜度分別如圖6、圖7、圖8所示。混沌圖的顏色程度代表了參數范圍內混沌系統的復雜程度。深色意味著系統具有較高的復雜度值，并且隨機性能良好。相反，淺色意味著隨機性能較差。當混沌系統用于安全通信時，系統參數的選擇應避開淺色區域。

3 基于超混沌系統的加密與解密算法

3.1 改進的Zigzag變換

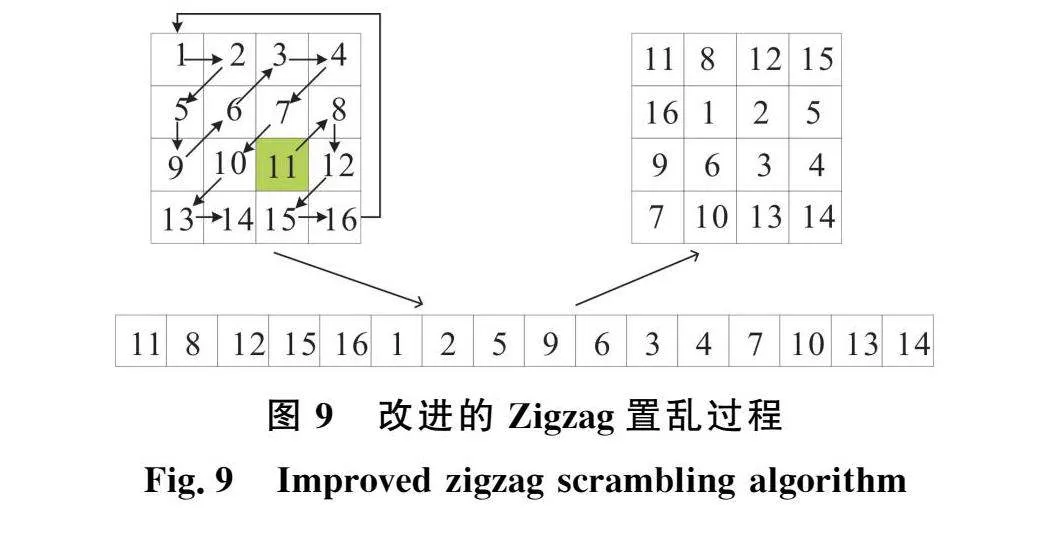
Zigzag變換是一種掃描置亂算法，標準的Zigzag變換過程是從矩陣的左上角數字開始，通過Z字型路徑依次取其他數字，將連續掃描得到的數字按某種方式重新組合成一個二維矩陣［3］。本文采用改進的Zigzag變換，從（3，3）位置處開始進行掃描，具體過程如圖9所示。

3.2 有限域理論

有限域GF（p）是整數的有限集合（p為素數），其基本的數學運算為模運算。本文使用有限域GF（257）={0， …，256}，其中257為素數。GF（257）的算術運算以257為模，此集合共包含257個元素。在乘法運算時，剔除元素0以減少因其造成的信息損失，這時集合中元素的個數為256，正好與圖像像素點灰度值的取值范圍對應。

將二維明文圖像矩陣按行或列展開為一維向量P，令C和S為密文向量，則i從1到MN的正向擴散算法為Ci=Ci－1×Si×Pi，其逆運算為Pi=Ci÷Ci－1÷Si，其中M為矩陣中的行數，N為矩陣中的列數。i從MN到1的逆向擴散算法為Ci=Ci+1×Si×Pi，其逆運算為Pi=Ci÷Ci+1÷Si。

3.3 加密算法

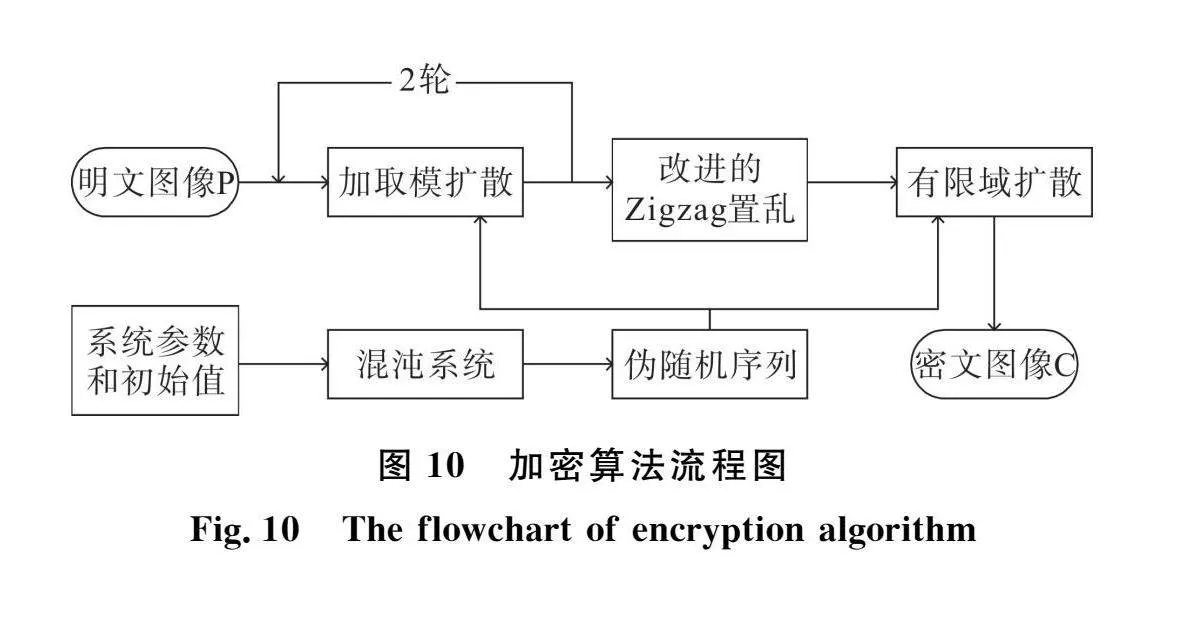
本文提出的基于復混沌系統的加密算法流程如圖10所示，具體步驟如下：

第1步：輸入明文圖像P（M×N），其中M為圖像的長度，N為圖像的高度。

第2步：設置算法的密鑰，即系統的參數和初值，讓系統（1）先迭代800次跳過過渡態，再迭代3MN次，生成4個長度為3MN的偽隨機序列x，y，z，w，結合式（9）得到4個長度為MN的偽隨機向量S S2，X X2：

S=mod（floor（x×pow2（16）），256）Q=mod（floor（y×pow2（16）），256）X=mod（floor（z（MN+1：3MN）×pow2（16）），256）Y=mod（floor（w（MN+1：3MN）×pow2（16）），256）S1=S（MN+1：2MN）S2=Q（MN+1：2MN）X1=X（MN+1：2MN）X2=Y（MN+1：2MN）（4）

第3步：利用向量S S2與式（5）將明文圖像P進行兩次加取模擴散得到圖像A。

Ai=（Ai－1+S1i+Pi）mod256Ai=（Ai+1+S2i+Pi）mod256（5）

其中，Ai，S1i，S2i，Pi分別代表A，S S2，P中的元素，i=，…，MN。

第4步：利用改進的Zigzag變換對擴散后的矩陣A進行置亂，得到圖像矩陣B。

第5步：利用向量X X2與式（6）對圖像B進行有限域擴散得密文圖像C。

Ci=Ci－1×X1i×BiCi=Ci+1×X2i×Bi（6）

其中，Ci，X1i，X2i，Bi均代表C，X X2，B中的元素，i=，…，MN。

解密過程為加密過程的逆過程，在此不再展示。

3.4 實驗結果

本次實驗采用尺寸為256×256的Camera、Lena圖像按照上述加密算法進行加密，實驗平臺為Inter（R）Core（TM）i57Y54CPU@1.20GHz，內存為8GB，操作系統為Windows 10，編程環境為MATLAB 2018b。設定算法的密鑰，其中參數設為a=14，b=0. c=3.7，r=45，初始值為（ 1）。經數值仿真得到Camera與boat的加密圖像與解密圖像，如圖11所示。顯然，加密后的圖像是類噪聲圖像，說明了本文設計的加密算法可以有效隱藏原始圖像信息。從解密結果來看，解密后的圖像與明文圖像并無差別，表明了解密算法的可行性。

4 性能分析

4.1 密鑰空間

一般來說，更大的密鑰空間，代表著算法有更好的安全性。本文設計的加密系統中的密鑰主要包括系統參數a，b，c，r和初值（u10，u20，u30，u40，u50）。其中初值與系統參數a，c的計算精度均為1015，b的計算精度為1017，r的計算精度為1014。因此，密鑰空間大小為1015×7+17+14≈2452。此值遠大于密碼學中密鑰空間的理論值2100，因此本文設計的加密算法可以有效抵抗窮舉暴力攻擊。表1展示了本文與參考文獻［6，7，10，14］設計的加密算法的比較結果。顯然，本文設計的加密算法的密鑰空間稍大于其他算法，這表明本文設計的算法具有極強的抗擊窮舉攻擊的能力。

4.2 密鑰敏感性分析

一個好的加密算法應該有較高的密鑰敏感性。本節采用Camera圖像進行測試，首先設置算法的密鑰a=14，b=0. c=3.7，r=45，u10=u20=u30=u40=u50=1。當使用正確密鑰時得到的解密圖像如圖12a所示。然后固定系統的初始值，對參數a，b，c，r分別施加10-15，10-17，10-15，10-14的微小擾動，得到解密后的Camera圖像如圖12b～e所示。顯然，密鑰產生微小改變后的解密圖像與使用正確密鑰解密后的圖像之間存在巨大差別，這說明本文設計的算法對密鑰極其敏感，能有效抵抗暴力攻擊。

4.3 信息熵

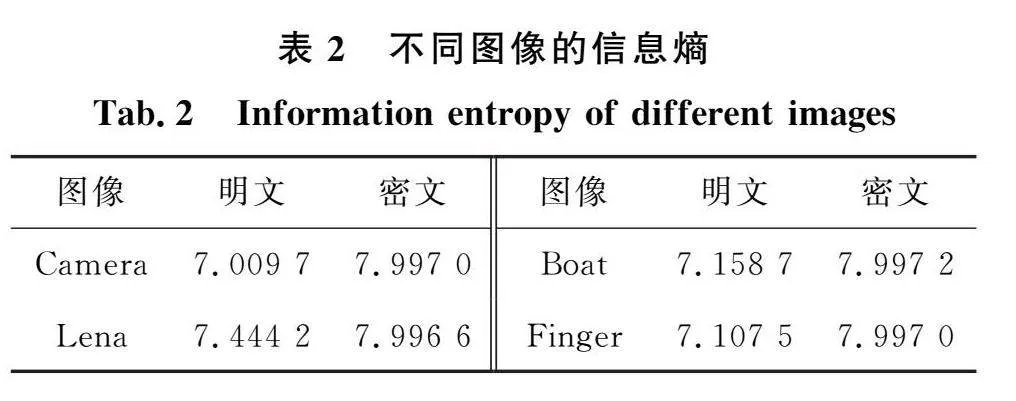
信息熵是反映圖像信息不確定性的重要參考。一般來說，隨著信息熵的增加，圖像信息也具有更大的不確定性和更少的可見性。對于像素值為256的圖像來說，信息熵的理論值為8。越接近理論值8，密文圖像的像素值分布的越均勻，安全性也越高。

本節計算了明文圖像Camera、Lena、Boat、Finger及其對應的加密圖像的信息熵，結果見表2。可以看出，密文的信息熵均接近于理論值8，這表明本文所設計的加密算法使明文圖像的像素值分布均勻，很好地隱藏了明文圖像的信息，具有較強的抵抗外部攻擊的能力。此外，將本文的Lena圖像的信息熵值與參考文獻［4，6，8，10，14］進行對比，結果如表3所示。從表3中可以看出，用本文所設計算法得到的密文圖像的信息熵較多數算法更接近于理論值，從而說明本文算法對于提高圖像加密的安全性更加有效。

4.4 直方圖

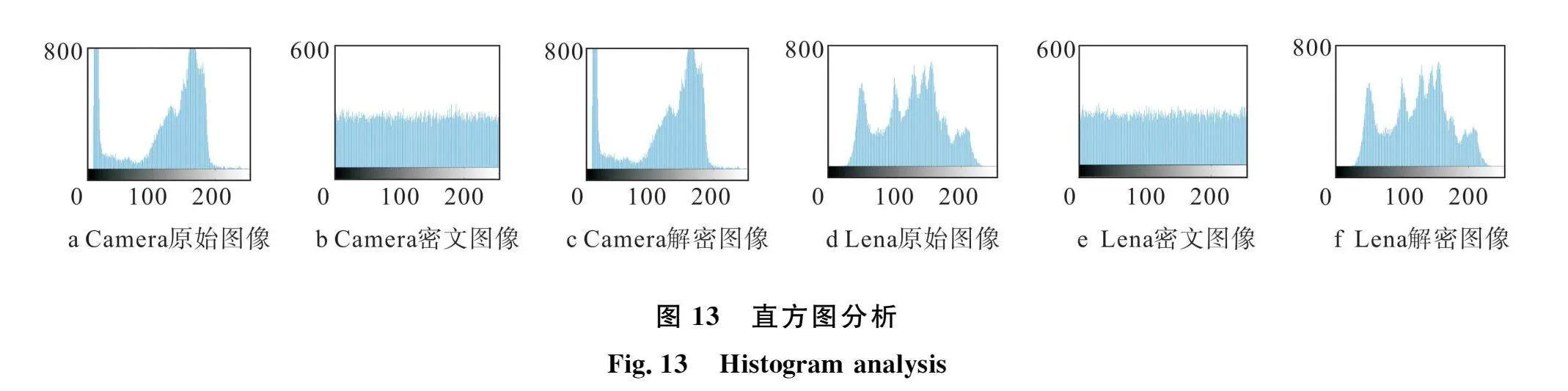
直方圖能直觀地反映圖像像素值的分布情況，常用于評價圖像抵抗統計攻擊的能力。密文圖像的像素值應呈均勻分布，且與明文圖像有明顯差異。本節采用Camera、Lena圖像進行測試，其中圖13a～c為Camera圖像測試結果，圖13d～f為Lena圖像測試結果。顯然，加密圖像的像素值分布均勻，而明文圖像的像素值分布波動較大。這說明，密文圖像抵御統計攻擊的能力較明文圖像更強，安全性更高。

4.5 相關性

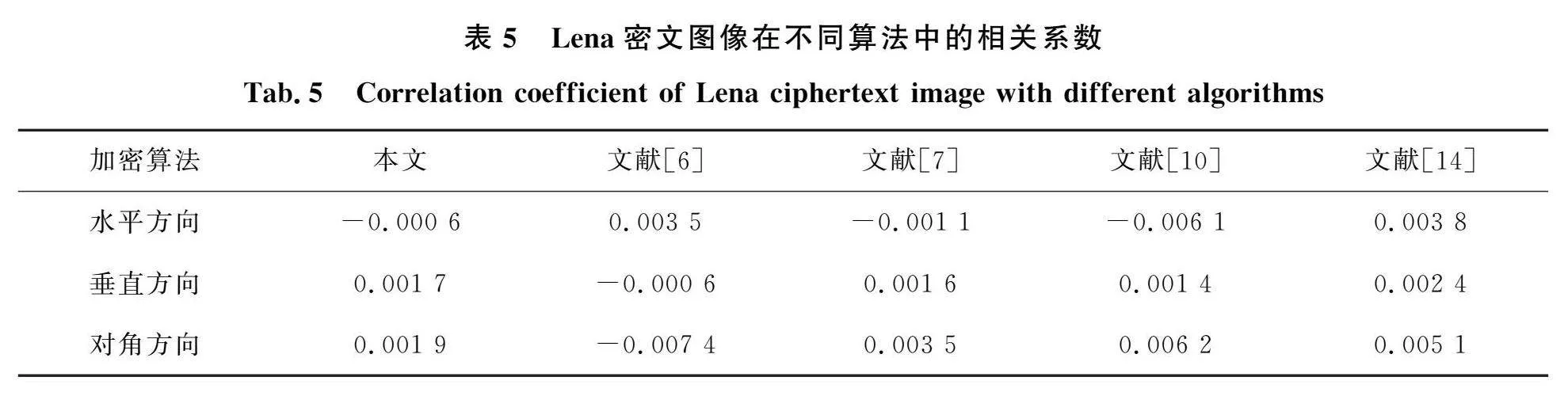
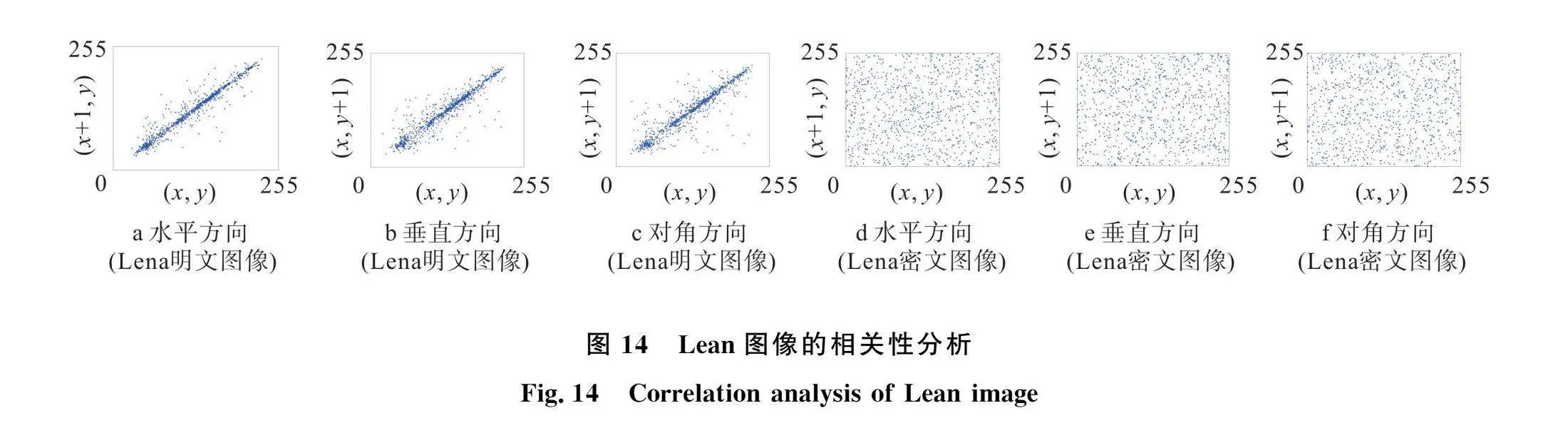
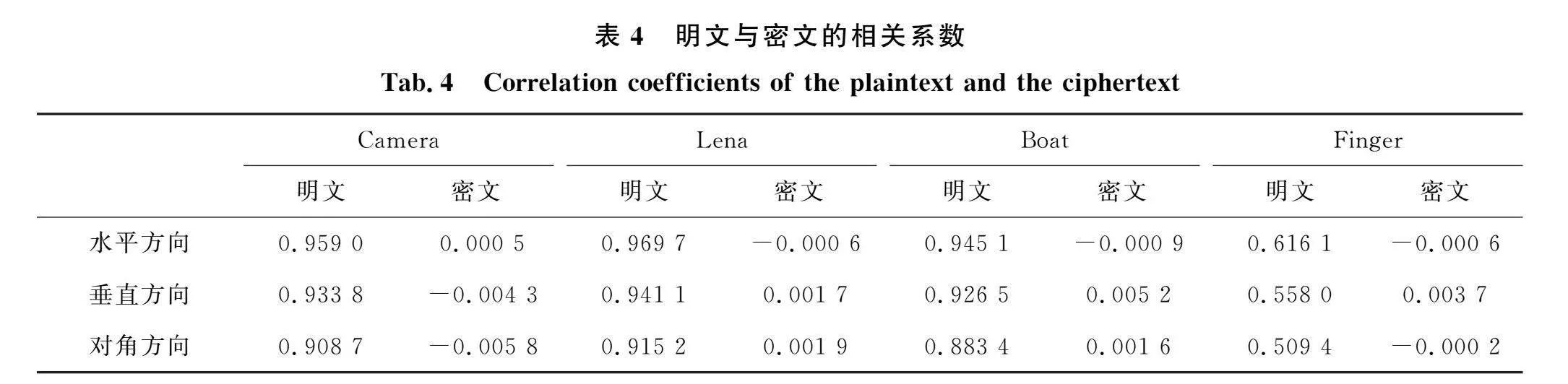
相關性是指圖像相鄰像素之間的關聯性，相關性越高，越容易被統計攻擊破解。因此，加密算法應有效降低明文圖像像素之間的相關性。本次測試分別對Camera、Lena、Boat和Finger的明文圖像與密文圖像在水平、垂直和對角方向各隨機選擇2 000對鄰域像素進行計算，結果如表4所示。選擇Lena明文圖像和Lena密文圖像的像素點集進行分析，得到兩幅圖像相鄰像素的相關系數如圖14所示。顯然，明文圖像的相鄰像素的灰度值在每個方向上均大致沿y=x分布。而密文圖像的相鄰像素的灰度值則是隨機分布在0到255之間。結果表明，本文設計的加密算法能有效降低相鄰像素的相關性。另外，表5中展示了本文與參考文獻［6，7，10，14］中Lena圖像的相關系數比較的結果。顯然，運用本文所設計的算法得到密文圖像的相鄰像素間的相關系數略低于其他算法，這說明本文設計的算法具有良好的抗統計攻擊能力。

5 總結

本文主要介紹了一個基于復混沌系統的圖像加密方案，方案利用了改進的Zigzag置亂、加取模擴散以及有限域擴散。首先對提出的系統進行基本的動力學分析，分析結果表明該系統是一個具有復雜動力學行為的超混沌系統。進而將其應用到設計的加密方案中，發現加密效果良好。接下來進行了安全性分析，利用密鑰空間、密鑰敏感性、信息熵、直方圖、相關性驗證了本文設計的加密方案具有很高的安全性，可以抵擋外部攻擊。未來的研究會繼續尋找動力學行為豐富的混沌系統并將其應用在圖像加密中。

參考文獻：

［1］王珠林， 閔富紅， 彭光婭， 等. 一個新三維混沌系統及其電路實現［J］. 南京師范大學學報（工程技術版）， 2016， 16（1）： 18.

WANG Z L， MIN F H， PENG G Y， et al. A three dimension chaotic system and its circuit realization［J］. Journal of Nanjing Normal University （Engineering and Technology Edition）， 2016， 16（1）： 18.

［2］MATTHEWS R. On the derivation of a “Chaotic” encryption algorithm［J］. Cryptologia， 1989， 13（1）： 2942.

［3］楊飛飛. 基于混沌序列的圖像加密算法研究［D］. 大連：大連工業大學， 2020.

YANG F F. Research on image encryption algorithm based on chaotic sequence［D］. Dalin： Dalian Polytechnic University， 2022.

［4］YOUSIF B， KHALIFA F， MAKRAM A， et al. A novel image encryption/decryption scheme based on integrating multiple chaotic maps［J］. AIP Advances， 2020， 10（7）： 19.

［5］SHI Q Q， AN X L， XIONG L， et al. Dynamic analysis of a fractional-order hyperchaotic system and its application in image encryption［J］. Physica Scripta， 2022， 97（4）： 045201.

［6］LIN R G， LI S. An image encryption scheme based on Lorenz hyperchaotic system and RSA algorithm［J］. Security and Communication Networks， 202 5： 118.

［7］徐昌彪， 孫義龍. 基于超混沌系統和有限域理論的圖像加密算法［J］. 信息通信， 2018， 7： 2123.

XU C B， SUN Y L. Image encryption algorithm based on hyper-chaotic system and finite field theory［J］. Information & Communications， 2018， 7： 2123.

［8］劉瀚揚， 華南， 王一諾， 等. 基于量子隨機行走和多維混沌的三維圖像加密算法［J］. 物理學報， 2022， 71（17）： 140155.

LIU H Y， HUA N， WANG Y N， et al. Three dimensional image encryption algorithm based on quantum random walk and multidimensional chaos［J］. Acta Physica Sinica， 2022， 71（17）： 140155.

［9］安新磊， 熊麗， 喬帥. 電磁驅動下一類混合神經元模型的動力學響應與圖像加密應用［J］. 電子與信息學報， 2023， 45（3）： 929940.

AN X L， XIONG L， QIAO S. Dynamic response of a class of hybrid neuron model by electromagnetic induction and application of image encryption［J］. Journal of Electronics & Information Technology， 2023， 45（3）： 929940.

［10］ YANG F F， MOU J， LIU J， et al. Characteristic analysis of the fractional-order hyperchaotic complex system and its image encryption application［J］. Signal Processing， 2020， 169： 107373.

［11］ 劉思聰， 李春彪， 李泳新. 基于指數余弦離散混沌映射的圖像加密算法研究［J］. 電子與信息學報， 2022， 44（5）： 17541762.

LIU S C， LI C B， LI Y X. A novel image encryption algorithm based on exponent-cosine chaotic mapping［J］. Journal of Electronics & Information Technology， 2022， 44（5）： 17541762.

［12］ 劉公致， 吳瓊， 王光義， 等. 改進型Logistic混沌映射及其在圖像加密與隱藏中的應用［J］. 電子與信息學報， 2022， 44（10）： 18.

LIU G Z， WU Q， WANG G Y， et al. A improved logistic chaotic map and its application in image encryption and hiding［J］. Journal of Electronics & Information Technology， 2022， 44（10）： 18.

［13］ 張文宇， 幸榮盈， 李國東. 基于改進Clifford混沌系統的圖像加密算法［J］. 電子技術應用， 2022， 48（6）： 7378.

ZHANG W Y， XING R Y， LI G D. Image encryption algorithm based on improved Clifford chaotic system［J］. Computer Technology and Its Application， 2022， 48（6）： 7378.

［14］ 葉瑞松， 習玉婷， 陳錦彬. 基于混沌映射和交換置換的自適應圖像加密算法［J］. 徐州工程學院學報（自然科學版）. 2022， 37（2）： 110.

YE R S， XI Y T， CHEN J B. A self-adaptive image encryption scheme based on chaotic map and swapping confusion approach［J］. Journal of Xuzhou Institute of Technology （Natural Sciences Edition）， 2022， 37（2）： 110.

［15］ 王樂元. 基于復混沌的彩色圖像加密算法研究與軟件實現［D］. 泰安： 山東農業大學， 2016.

WANG L Y. Algorithm of color image encryption and its software implementation based on complex chaotic systems［D］. Taian： Shandong Agricultural University College， 2016.

［16］ 王文靜， 安新磊， 于歡歡. 具有隱藏吸引子的混沌系統的動力學分析［J］. 寧夏大學學報（自然科學版）， 2019， 40（3）： 224228.

WANG W J， AN X L， YU H H. Dynamic analysis of chaotic systems with hidden attractors［J］. Journal of Ningxia University （Natural Science Edition）， 2019， 40（3）： 224228.

（責任編輯 耿金花）