基于數學核心素養視角下的初中課堂教學思考與實踐


【摘要】本文從初中數學知識“勾股定理”入手,提出基于數學核心素養視角下的初中課堂教學新思考與新實踐,為促進學生數學核心素養的提升提供力所能及的幫助.
【關鍵詞】核心素養;初中數學;課堂教學
1 引言
勾股定理是初中數學教學中極其重要的概念與工具,也是學生初中數學學習中的重難點,需要教師給予高度重視,促進學生全面進步發展.
2 基于數學核心素養視角下的初中課堂教學新思考與新實踐
傳統的勾股定理教學知識記憶化、探究形式化以及目標應試化現象相對嚴重,因此,教師應該從打造動態化課堂入手,讓學生學會利用實踐、猜想、發現、驗證、證明多元化方式完成學習,提升自身綜合能力.
3 基于數學核心素養視角下的初中數學解題技巧及案例分析
3.1 勾股定理的應用技巧
3.1.1 求解三角形邊長問題
例1 已知△ABC中,AB=17cm,AC=10cm,BC邊上的高AD=8cm,則邊BC的長為.
解析 本題既考查學生的繪圖能力,也考查學生解題中的分類討論能力.因此,需要教師在課堂教學中針對這兩個方面給予高度的重視與引導.
解 已知△ABC中,AB=17cm,AC=10cm,AD=8cm,
由勾股定理可得,
BD=AB2-AD2=172-82=15cm,
CD=AC2-AD2=102-82=6cm,
如圖1所示,假設點D位于邊BC上,
則BC=CD+BD=15+6=21cm,
如圖2所示,若點D位于BC的延長線上,
則BC=BD-CD=15-6=9cm.
所以邊BC的長為21cm或9cm.
例2 在△ABC中,AB=30,AC=25,BC邊上的高AD為24,則△ABC的面積為.
解析 這一題是例1的變式,教師需要引導學生在充分掌握勾股定理的基礎上,對三角形的分類及分類條件等有較為清晰地掌握.
解 已知△ABC中,AB=25,AC=30,AD=24,
由勾股定理可得,
BD=AB2-AD2=302-242=18,
CD=AC2-AD2=252-242=7,
如圖3所示,假設點D位于邊BC上,且AD⊥BC,
則BC=CD+BD=7+18=25,
則S△ABC=12·BC·AD=12×25×24=300,
如圖4所示,若點D位于BC的延長線上,
則S△ABC=S△ABD-S△ACD=12·BD·AD-12·CD·AD=12×18×24-12×7×24=132.
所以△ABC的面積為300或132.
3.1.2 判斷三角形類型
例3 已知三角形的三邊長分別為a,b,c,且滿足a+b=10,ab=18,c=8,則該三角形是.
解析 此處考查學生對勾股定理逆定理的掌握情況,教學中需要充分引導學生學會借助已有條件對三角形的三邊關系進行推導.
解 已知a+b=10,ab=18,c=8,
由勾股定理逆定理可得
a2+b2=a+b2-2ab=100-36=64,
又因為c2=64,
所以a2+b2=c2,則由此可知該三角形為直角三角形.
例4 如圖5,△ABC中,AB=AC=5cm,BC=8cm,動點D在底邊上從B向C以0.25cm/s的速度移動,當點P運動幾秒時,點P與頂點A的連線PA與腰垂直.
解析 此題考查學生對等腰三角形基本知識的掌握情況,解題關鍵是學生需要扎實掌握勾股定理并化難為簡.
解 如圖5,作AD⊥BC,交BC于點D,已知△ABC是等腰三角形,
則BD=CD=12BC=4cm,
在△ABD中,AD=AB2-BD2=3cm,
如圖6所示,當點P運動t秒后有PA⊥AC時,
由AP2=PD2+AD2=PC2-AC2,
可知PD2+32=PD+42-52,
因此PD=2.25cm,
則BP=4-2.25=1.75=0.25t,故而t=7s.
如圖7所示,當點P運動t秒后有PA⊥AB時,同理可證得PD=2.25,則BP=4+2.25=6.25=0.25t,即t=25s.
故而點P運動的時間為7秒或25秒.
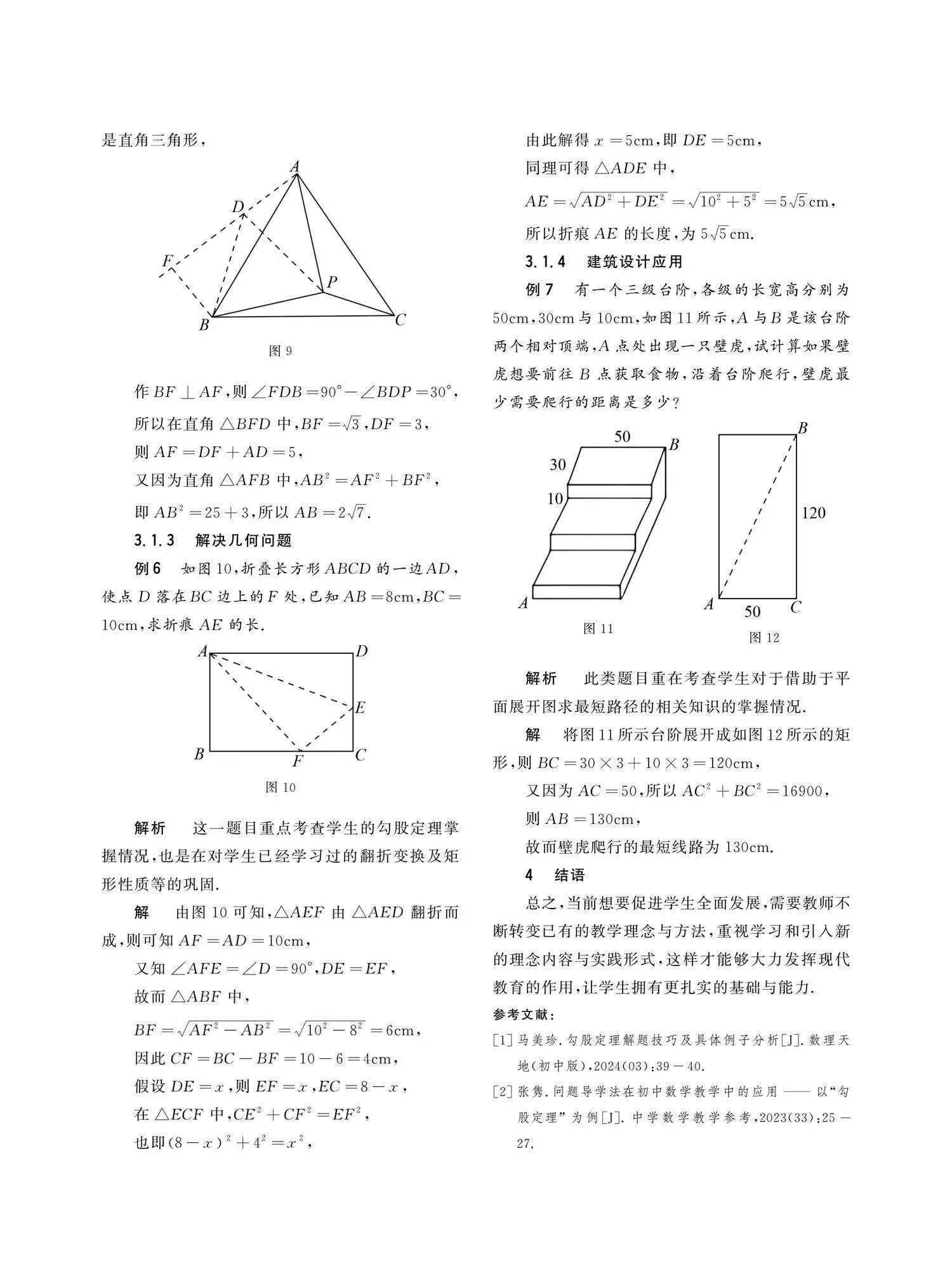
例5 如圖8所示,等邊△ABC中有一點P,已知PA=4,PB=23,PC=2,則AB=.
解析 這道題目放在判斷三角形類型中進行解析分析,學生預解此題,需先將三條線段不在同一個三角形中的三角形旋轉60°后構造直角三角形,再以勾股定理進行解題.
解 將△BPC繞點B逆時針旋轉60°后得△BDA,如圖9所示,故而∠DBP=60°,
又因為PB=23,DB=PB,
則DB=23,△BDP是等邊三角形,
故而PD=23,
又因為DA=PC=2,PA=4,
則可得DA2+PD2=PA2,因此證實△ADP是直角三角形,
作BF⊥AF,則∠FDB=90°-∠BDP=30°,
所以在直角△BFD中,BF=3,DF=3,
則AF=DF+AD=5,
又因為直角△AFB中,AB2=AF2+BF2,
即AB2=25+3,所以AB=27.
3.1.3 解決幾何問題
例6 如圖10,折疊長方形ABCD的一邊AD,使點D落在BC邊上的F處,已知AB=8cm,BC=10cm,求折痕AE的長.
解析 這一題目重點考查學生的勾股定理掌握情況,也是在對學生已經學習過的翻折變換及矩形性質等的鞏固.
解 由圖10可知,△AEF由△AED翻折而成,
則可知AF=AD=10cm,
又知∠AFE=∠D=90°,DE=EF,
故而△ABF中,
BF=AF2-AB2=102-82=6cm,
因此CF=BC-BF=10-6=4cm,
假設DE=x,則EF=x,EC=8-x,
在△ECF中,CE2+CF2=EF2,
也即8-x2+42=x2,
由此解得x=5cm,即DE=5cm,
同理可得△ADE中,
AE=AD2+DE2=102+52=55cm,
所以折痕AE的長度,為55cm.
3.1.4 建筑設計應用
例7 有一個三級臺階,各級的長寬高分別為50cm,30cm與10cm,如圖11所示,A與B是該臺階兩個相對頂端,A點處出現一只壁虎,試計算如果壁虎想要前往B點獲取食物,沿著臺階爬行,壁虎最少需要爬行的距離是多少?
解析 此類題目重在考查學生對于借助于平面展開圖求最短路徑的相關知識的掌握情況.
解 將圖11所示臺階展開成如圖12所示的矩形,
則BC=30×3+10×3=120cm,
又因為AC=50,所以AC2+BC2=16900,
則AB=130cm,
故而壁虎爬行的最短線路為130cm.
4 結語
總之,當前想要促進學生全面發展,需要教師不斷轉變已有的教學理念與方法,重視學習和引入新的理念內容與實踐形式,這樣才能夠大力發揮現代教育的作用,讓學生擁有更扎實的基礎與能力.
參考文獻:
[1]馬美珍.勾股定理解題技巧及具體例子分析[J].數理天地(初中版),2024(03):39-40.
[2]張雋.問題導學法在初中數學教學中的應用——以“勾股定理”為例[J].中學數學教學參考,2023(33):25-27.

