聚焦經典習題 開啟思維之門

教材中的例題和習題為我們提供了經典的解題思路和方法。下面以蘇科版數學教材九（上）第117頁的習題為例，談談對經典習題的學習與思考。

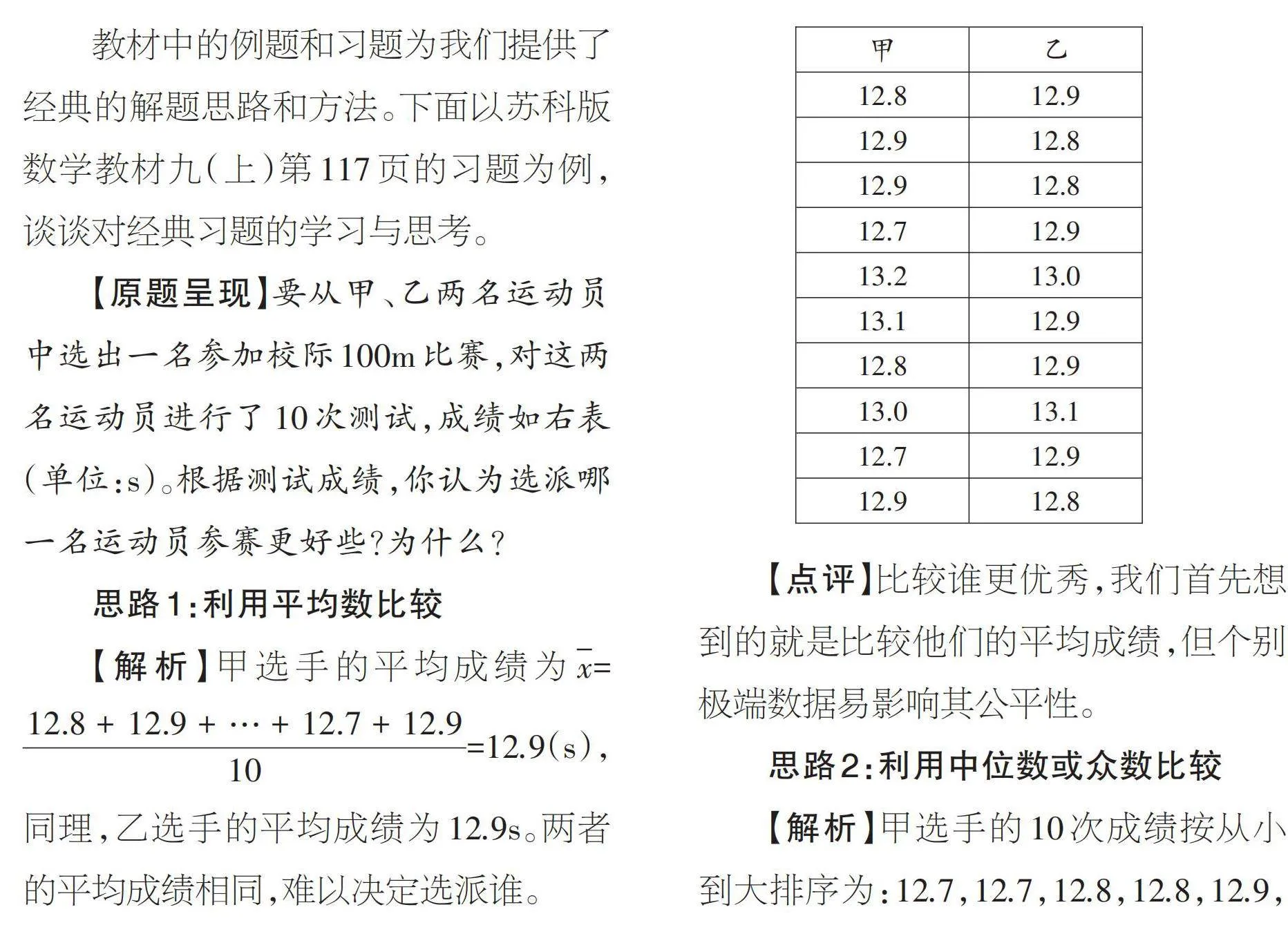
【原題呈現】要從甲、乙兩名運動員中選出一名參加校際100m比賽，對這兩名運動員進行了10次測試，成績如右表（單位：s）。根據測試成績，你認為選派哪一名運動員參賽更好些？為什么？

思路1：利用平均數比較

【解析】甲選手的平均成績為[x]=[12.8+12.9+…+12.7+12.910]=12.9（s），同理，乙選手的平均成績為12.9s。兩者的平均成績相同，難以決定選派誰。

【點評】比較誰更優秀，我們首先想到的就是比較他們的平均成績，但個別極端數據易影響其公平性。

思路2：利用中位數或眾數比較

【解析】甲選手的10次成績按從小到大排序為：12.7，12.7，12.8，12.8，12.9，12.9，12.9，13.0，13.1，13.2，則中位數是[12.9+12.92]=12.9（s），眾數為12.9s；同理，乙選手成績的中位數是12.9s，眾數為12.9s。我們發現兩者的中位數與眾數也相同，因此，仍然難以決定選派誰。

【點評】中位數與眾數也是我們分析數據集中趨勢的常用度量指標。中位數是將一組數據按照從小到大順序排列后，最中間的那個數或最中間兩個數的平均數，而眾數是一組數據中出現次數最多的那個數。眾數不唯一，并且改變部分數據不一定影響中位數與眾數。

思路3：利用極差比較

【解析】甲選手10次成績的極差為13.2-12.7=0.5（s），乙選手10次成績的極差為13.1-12.8=0.3（s）。因為0.3＜0.5，所以乙選手10次成績波動范圍更小，選擇乙選手更為適合。

【點評】極差是用一組數據的最大值減去最小值所得的差來反映這組數據的變化范圍，是刻畫數據離散程度最簡單的統計量。但極差只利用了一組數據兩端的信息，看的是較粗略的離散情況，不能準確反映中間數據的離散程度。

思路4：利用平均差比較

【解析】平均差是一組數據中的每一個數據與它們的平均數的差的絕對值的平均數。由數據求得甲的平均成績為12.9s，乙的平均成績為12.9s，則甲數據的平均差為：[110]（[12.8-12.9]+…+[12.9-12.9]）=0.12（s），同理，求得乙數據的平均差為0.06s。因為0.06＜0.12，所以選擇乙選手參加比賽。

【點評】平均差反映一組數據中每個數值與該組數據算術平均數之間的平均差異。平均差越小，說明數據越接近平均值，該算術平均數的代表性就越大。

思路5：利用方差或標準差比較

【解析】方差是一組數據中每個數據與它們的平均數的差的平方的平均數。計算甲的方差為0.024（s2），乙的方差為0.008（s2）。因為0.008＜0.024，所以乙選手更為穩定。

【點評】方差反映一組數據偏離平均數的大小，但是其數量單位與原數據的數量單位不一致，因此在實際應用時，常常將求出的方差再開平方，這就是標準差。

可見，平均數、中位數、眾數反映一組數據的集中趨勢，極差、平均差、方差、標準差反映一組數據的離散程度。相對而言，方差更能反映一組數據的波動大小，因此，在平均數相近的情況下，通過計算方差來確定參賽運動員比較合適。

（作者單位：江蘇省興化市板橋初級中學）