不同偏壓下半導體器件能帶圖的繪制研究
摘要:能帶圖在半導體物理與器件的學習中占據重要地位。深入分析PN(PNJunction)結在零偏、正偏和反偏電壓下能帶圖的區別與聯系,得到PN結能帶圖繪制的一般規律,并推廣這個一般規律。把金半(MetalSemiconductor,MS)接觸結構當作PN結的特例直接套用PN結中總結的規律,得到MS結構的能帶圖。再利用介質中的電位移連續性直接得到金屬-氧化物-半導體(MetalOxideSemiconductor,MOS)結的能帶圖,認為總結的規律好學易用,可推廣。
關鍵詞:PN結MS結MOS結正反偏能帶圖
ResearchontheDrawingofEnergyBandDiagramofSemiconductorDevicesUnderDifferentBiasVoltages
HAOWenfeiZOULiZHANGZhendongZHANGHaotianYINChaopeng
SONGXiaonaMENGQingduan*
CollegeofInformationEngineering,HenanUniversityofScienceandTechnology,Luoyang,He’nanProvince,471000China
Abstract:Banddiagramplaysanimportantroleinthestudyofsemiconductorphysicsanddevices.ThedifferenceandrelationshipbetweentheenergybanddiagramsofPNJunction(PN)junctionsunderbias,forwardandreversebiasvoltagesareanalyzedindepth,andthegenerallawofPNjunctionbanddiagramdrawingisobtained,andthisgenerallawispromoted.TheMetalSemiconductor(MS)contactstructureisregardedasaspecialcaseofthePNjunctionandtherulessummarizedinthePNjunctionaredirectlyappliedtoobtaintheenergybanddiagramoftheMSstructure.TheenergybanddiagramoftheMetalOxideSemiconductor(MOS)junctionisdirectlyobtainedbyusingtheelectricaldisplacementcontinuityinthereusemedium,anditisbelievedthatthesummarizedlawiseasytolearnandeasytouse,andcanbepromoted.
KeyWords:PNjunction;MSjunction;MOSjunction;Forwardandreversebias;Energybanddiagram
PN(PNJunction)結和金屬-氧化物-半導體(MetalOxideSemiconductor,MOS)結構是半導體器件中的兩種基本結構,它們在光電器件和集成電路等領域有著廣泛應用。正確繪制能帶圖對理解半導體器件的工作原理起著決定性的作用,可以幫助人們深入理解器件的導電特性、擊穿特性以及載流子輸運等核心物理過程[1]。本文以PN結正、反偏下的能帶圖繪制為例,得到PN結在正、反偏下能帶圖繪制的一般規則。將金半(MetalSemiconductor,MS)接觸作為PN結的特例,同時借助電介質中電位移連續的約束,直接得到MOS結構在正、反偏下的能帶圖。這一構想從具體例子得到一般規律,再演繹到特殊實例,可歸納,可演繹,能夠提升對器件工作原理的深入理解,具有指導意義。
1模型的建立
1.1正反偏條件下PN結能帶圖的繪制
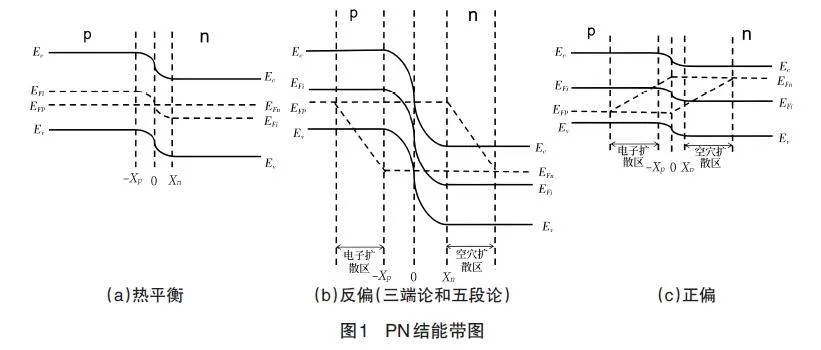
PN結能帶圖的繪制規則:(1)接觸前P型半導體和N型半導體能帶圖的繪制;(2)接觸后二者具有統一的費米能級,即以P型半導體為基準,把N型半導體的能帶圖往下平移,使二者的費米能級保持在同一水平位置[2];(3)在空間電荷區處,能帶圖以反“S”形連接兩側的P型半導體和N型半導體,即可得到空間電荷區中電子應遵循的電勢能()分布;(4)把往下平移即可得到,最后即可得到完整的PN結在零偏下的能帶圖,如圖1(a)所示。
PN結兩端加反向電壓,與內建電場的方向一致,增強了空間電荷區的電場,使空間電荷區展寬,勢壘高度也由零偏時的增加到,反向電壓的施加打破了零偏時載流子擴散與漂移之間的動態平衡,使得漂移運動強于擴散運動。勢壘高度也由e增高為(+),空間電荷區的費米能級之差,這里低于。空間電荷區兩側,少子從空間電荷區邊界處的最小值逐步增加到遠離邊界處半導體中的正常值,空間電荷區兩側少子分布是指數的,在能帶圖上顯示為準費米能級與X呈線性關系[3]。如圖1(b)所示。
反偏時,PN結的能帶圖從零偏時的三段過渡到反偏時的五段,即在零偏時PN結空間電荷區的兩側添加了兩個少子擴散區,這里少子從P和N區分別向空間電荷區擴散。空間電荷區的電場增強了,表現為空間電荷區和的斜率的絕對值更大,斜率的符號表示電場的方向與坐標系方向的異同。由此認為反偏就是外加電場與內建電場方向保持一致的狀態[4]。
正偏時,外加電場與內建電場相反,疊加的結果削弱了空間電荷區的電場。在少子擴散區中,準費米能級隨位置呈線性變化[5],如圖1(c)所示。
1.2PN結正反偏能帶圖繪制規則“五段論”
(1)接觸前,分別繪制P型和N型半導體的能帶圖。
(2)接觸后,如果沒有外加偏壓,PN結具有統一的費米能級。
(3)空間電荷區能帶圖的繪制,沿對稱軸劈開拋物線,取其右半部分,把左側部分沿水平軸翻轉180°,把反轉后的部分往右平移至PN結的界面處,與拋物線的右半部分相連接,隨后在連接處沿水平軸翻轉180°得到反形“S”結構。把反形“S”結構連接兩邊的P型、N型半導體的能帶圖,即得到零篇下PN結能帶圖繪制的三段論。反形“S”曲線的繪制也可采用如下的判據,接觸后半導體表面的電子濃度如果比體內的電子濃度低,則半導體表面的能帶相對于體內往上彎曲,反之則往下彎曲。半導體表面電子濃度的增減由接觸前費米能級的相對位置決定,電子從費米能級高的地方流入費米能級低位置。
(4)施加偏壓后,PN結處于非平衡狀態,空間電荷區統一的費米能級分裂成電子和空穴的準費米能級,其中多子的準費米能級維持不變,少子的準費米能級大幅偏離零偏時系統的費米能級,準費米能級之差即為外加偏壓與電荷的乘積。反偏時,相對于下移,正偏時,則相對于移。
(5)在空間電荷區的兩側,形成兩個少子擴散區,少子擴散區的兩側為中性區,在少子擴散區,少子的準費米能級隨坐標呈線性關系,向中性區費米能級靠攏。
1.3PN結正反偏能帶圖繪制規則的應用
1.3.1實例1:金半接觸
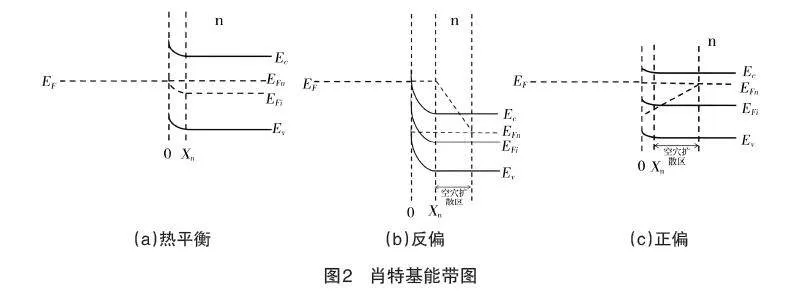
當PN結中P區的摻雜濃度接近原子濃度時,其導電性接近于金屬,所以MS結可以看作PN結的一個特例。運用上述PN結的繪制規則,很容易就能得到各種偏壓下金半接觸的能帶圖。重摻雜的P型半導體直接用費米能級替換,即把費米能級放置于P型半導體能帶圖中的處。對于重摻雜的P型半導體來說,電子的流出與流入與自身的多子濃度相比,可以忽略,故此重摻雜P型半導體中的能帶不發生彎曲[6]。
金屬(重摻雜P型半導體)與N型半導體接觸時,接觸前,若金屬費米能級的位置低于N型半導體費米能級的位置,則電子從N型半導體流入金屬,接觸后,N型半導體表面的能帶相對于體內往上彎曲,像PN結能帶圖中N型區的能帶圖那樣。接觸后,把PN結能帶圖中P型區一側直接用費米能級替換就得到了零偏時金屬與N型半導體接觸后的能帶圖,如圖2(a)所示。同理,加偏壓時,把重摻雜部分用費米能級直接替換就得到了金半接觸在不同偏壓下的能帶圖[7]。替換后的能帶圖如圖2(b)和2(c)所示。
1.3.1實例2:金屬-氧化物-半導體結構
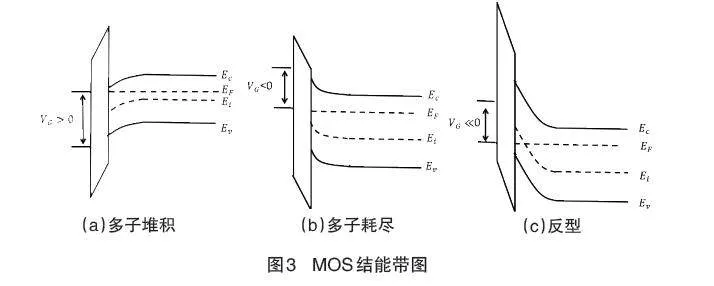
在MS結的基礎上,在界面處添加一層氧化物絕緣層,就把MS結轉變為MOS結。表面勢及空間電荷區內的電荷分布情況隨金屬與半導體間的增加而變化,基本上可歸納為堆積、耗盡和反型三種情況。根據金半接觸正反偏下的繪制規則及介質的電位移連續性(交界處氧化層導帶底斜率與氧化層介電常數的乘積等于交界處半導體導帶底斜率與半導體介電常數的乘積),即可畫出正反偏下MOS結的能帶圖。
當金屬與半導體之間加正電壓時,表面層形成多數載流子電子的堆積如圖3(a)所示,耗盡狀態是反型的前一個過程,先多子耗盡,當金屬與半導體間加不太高的負電壓時,即反偏,如圖3(b)所示,當負電壓進一步增大,表面層內形成由少數載流子堆積的反型層,表面處的能帶相較于體內進一步向下彎曲,只需把耗盡時的能帶圖讓能帶進一步彎曲即可,如圖3(c)。
2結語
PN結施加偏壓后,能帶圖變為“五段論”,電子擴散區和空穴擴散區兩側的能帶圖為接觸前P型、N型半導體的能帶圖;電子擴散區與空穴擴散區的能帶圖為準費米能級與中性P區、N區距離的線性表達;空間電荷區內的能帶圖為二次曲線或更高次的曲線,取決于摻雜分布,總體線型呈現反“S”型。繪制金半接觸的能帶圖直接套用PN結的規律,而金屬-氧化物-半導體結構的能帶圖根據金半接觸正反偏下的繪制規則及介質的電位移連續性可直接繪出。
參考文獻
- 楊杜娟.CsSnI3-BP異質結的界面特征和光電特性的第一性原理研究[D].長沙:湖南大學,2022.
- 楊佳東,楊占金,汪海玲,等.CdS基復合納米材料光催化制氫的研究進展[J].山東化工,2023,52(9):61-64,68.
- 母恒恒.硅漂移探測器的結構優化與網型小像素探測器的性能研究[D].湘潭:湘潭大學,2022.
- 翁加付.氮化鎵半導體器件的性能優化仿真及制備研究[D].桂林:桂林理工大學,2023.
- 李曉.一種新型高精度低功耗的數字溫度傳感器設計[J].集成電路應用,2023,40(8):16-18.
- 呂肖林.0.3THz單片集成倍頻器[D].成都:電子科技大學,2020.
- 彭博,李奇,張舒淼,等.金剛石肖特基二極管的研究進展[J].人工晶體學報,2023,52(5):732-745.

