面向組網雷達干擾任務的多機伴隨式編隊航跡預規劃方法

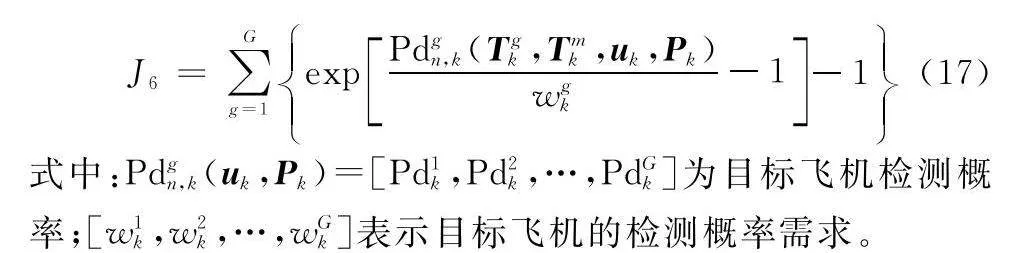
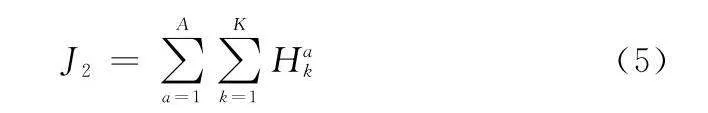
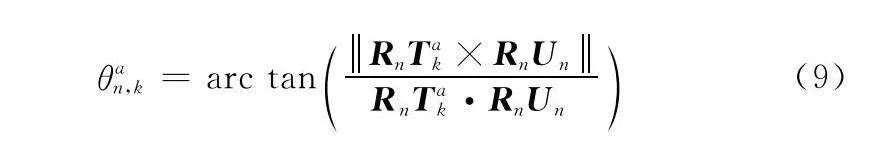
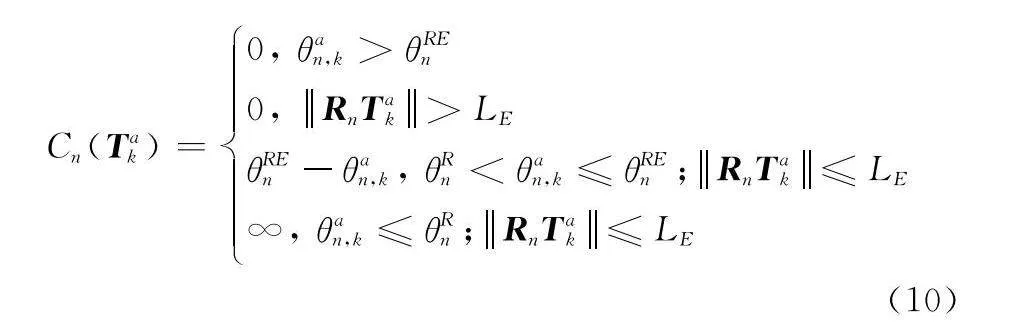
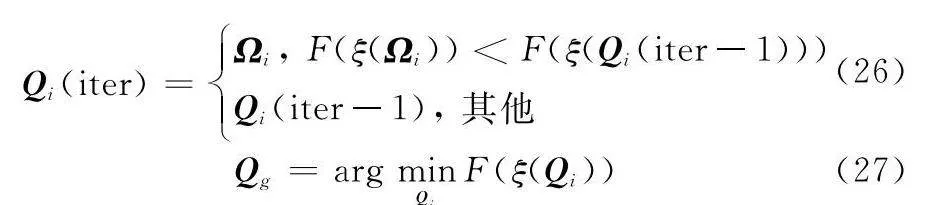
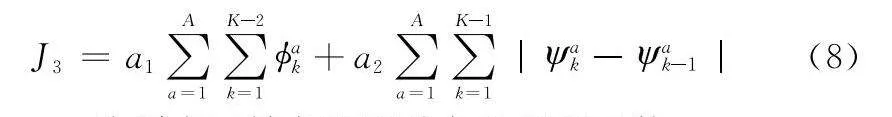
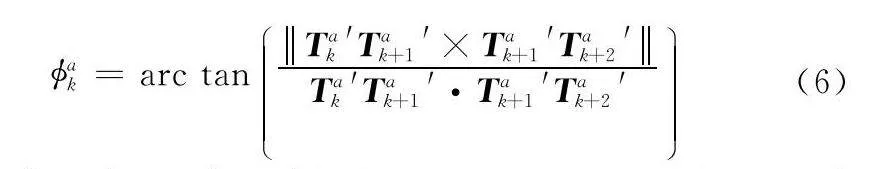
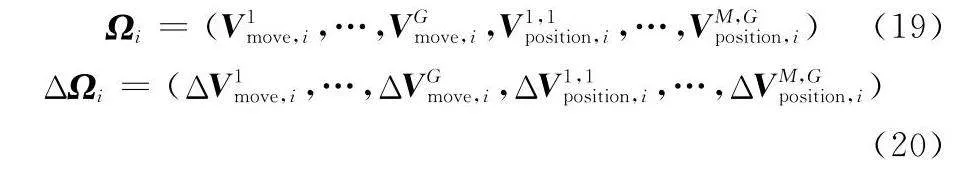
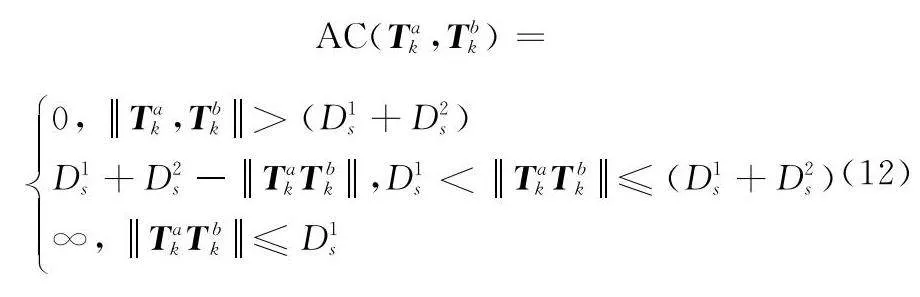
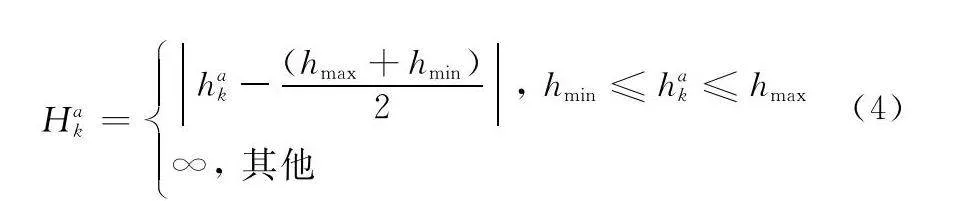
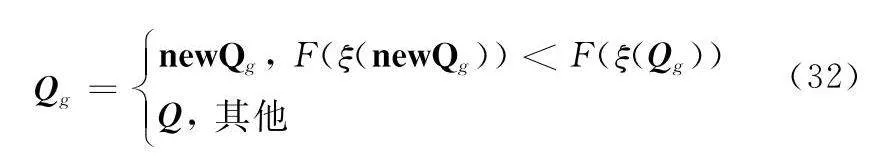
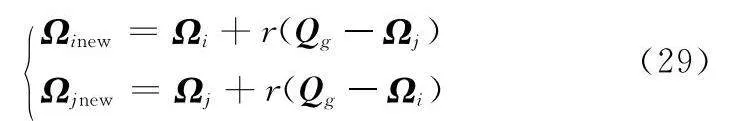
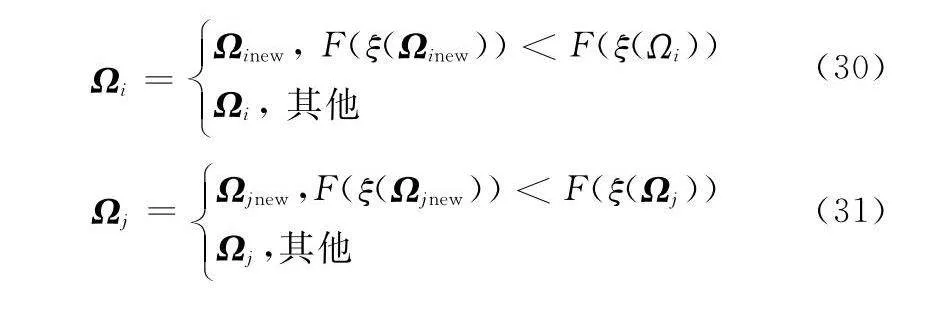
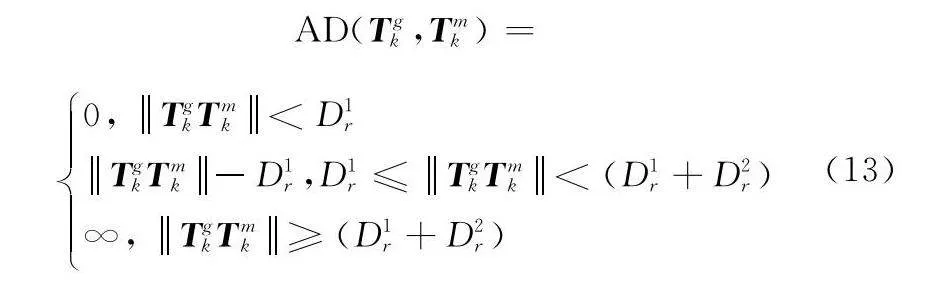
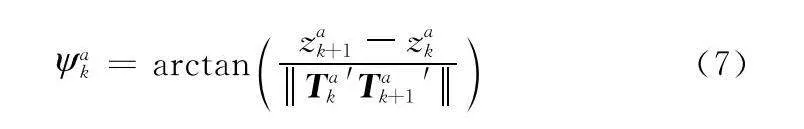
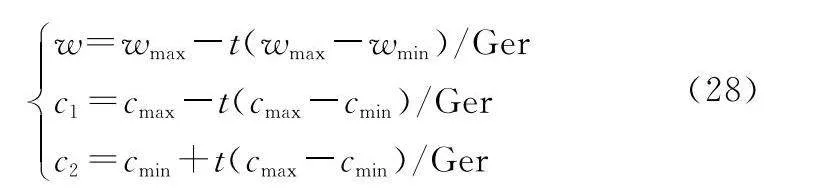
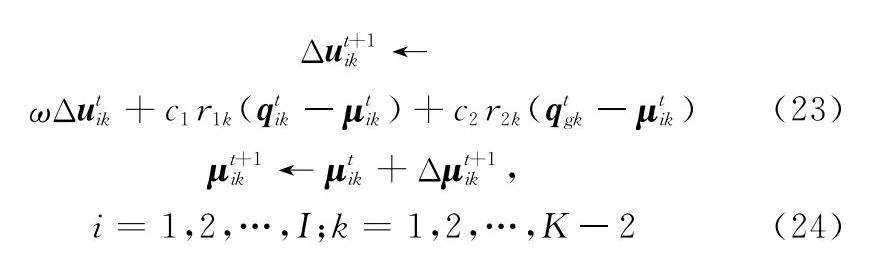
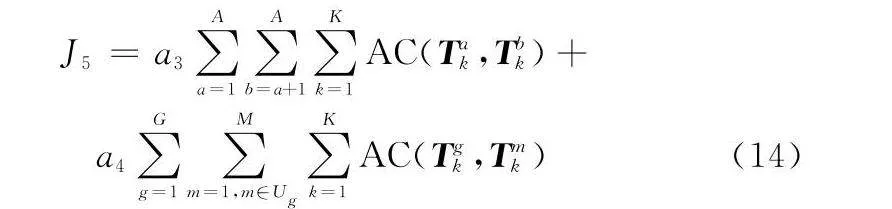
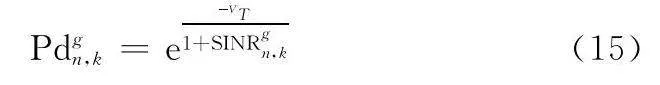
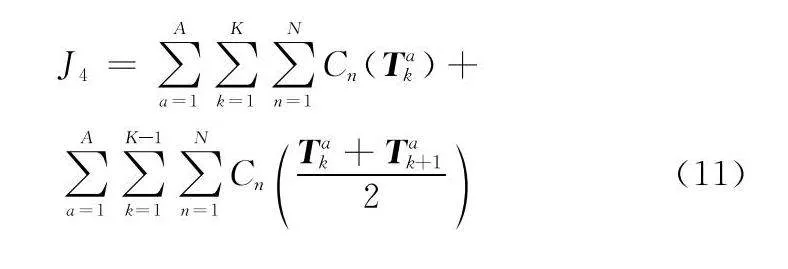
摘 要： 針對多目標突防組網雷達系統場景，為有效提高干擾效果以及突防成功率，編隊航跡規劃尤為重要。因此，首先構建航跡規劃模型，從飛行器自身約束、航跡安全性、機間協調以及任務完成效果4個方面出發，結合多機伴隨式編隊及其所處環境特點，提出較為完備的航跡規劃準則，形成一個新的整體目標函數;其次，為有效描述每架飛機的機動特性以及伴飛干擾機與目標飛機間的聯系，提高算法搜索能力，提出基于多球面矢量（multi-spherical vector-based， MS）方法;為進一步提高算法的探索和開發能力，提出多面球矢量逐航跡點學習混合粒子群優化（multi-spherical vector-based hybrid particle swarm optimization with track point by track point learning， TLHPSO）算法，并將兩者相結合，形成基于多面球矢量的逐航跡點學習混合粒子群優化（MS-based hybrid particle swarm optimization with track point by track point learning， MS-TLHPSO）航跡規劃方法;最后，構建相應仿真場景進行驗證。對比結果表明，MS方法以及TLHPSO優化算法在尋優能力上具有明顯優勢;同時，所提算法在不同初始場景下最優解的平均值均優于其他算法，充分說明所提算法能夠在保證穩定性的前提下規劃具有更高可信度的編隊航跡。

關鍵詞： 組網雷達; 編隊航跡; 規劃準則; 多球面矢量; 逐航跡點學習

中圖分類號： TN 974

文獻標志碼： A

DOI：10.12305/j.issn.1001-506X.2024.08.28

Multi-syndrome jammers formation trajectory preplanning method for

netted radar jamming task

ZOU Weiqi， NIU Chaoyang^*， LIU Wei， WANG Yanyun， ZHAN Jiaqi

（School of Data and Target Engineering， PLA Strategic Support Force Information

Engineering University， Zhengzhou 450001， China）

Abstract： For the multi-target penetrating netted radar system scenario， in order to effectively improve the interference effect and penetration success rate， formation trajectory planning is particularly important. Therefore， this paper firstly builds a trajectory planning model. Starting from the four aspects of the aircraft’s own constraints， trajectory safety， constraints among aircrafts， and task completion effect， combined with the characteristics of the multi-syndrome jammers formation and its environment， a relatively complete trajectory planning criterion is proposed to form a new overall objective function. Secondly， in order to effectively describe the maneuver properties of each aircraft and the connection between the accompanying jammer and the target aircraft， and improve the algorithm’s search ability， a multi-spherical vector-based （MS） method is proposed. At the same time， in order to further improve the exploration and development capabilities of the proposed algorithm， a hybrid particle swarm optimization with track point by track point learning （TLHPSO） algorithm is proposed， and the two algorithms are combined to form MS-TLHPSO trajectory planning method. Finally， the simulation scenarios are constructed for verification. The comparison results show that the MS method and the TLHPSO optimization algorithm have obvious advantages in the ability to find the optimal value. The proposed algorithm in this paper is superior to other algorithms in terms of the average value of the optimal solution in different initial scenarios， which fully shows that the algorithm in this paper can plan formation tracks with higher reliability under the premise of ensuring stability.

Keywords： netted radar; formation trajectory; planning criterion; multi-spherical vector; track point by track point learning

0 引 言

隨著信號處理以及組網技術的發展，組網雷達已經成為對抗電子干擾的重要手段，相較于傳統單基地雷達，組網雷達測量精度以及識別能力大大提高，并且利用數據的互聯互通，能夠充分發揮協同對抗的優勢。

在多目標突防組網雷達場景中，組網雷達給進攻方飛行器帶來了巨大威脅，進攻方機群為了有效完成任務，需盡可能避免組網雷達的探測。然而，僅有一類機群難以滿足雷達探測條件，即進攻方機群往往為多機伴隨式編隊，由目標機群和伴隨式干擾機群構成。因此，在實際應用過程中合理規劃編隊航跡顯得尤為重要，其能夠有效降低組網雷達的探測威脅，同時合理規劃干擾機群與目標機群間的關系，可以有效降低組網雷達防御范圍，進一步提高干擾效果及突防成功率^［1］。

現階段，航跡規劃被廣泛應用于民用和軍用場景^［2-5］，多機編隊航跡規劃指的是在三維空間中規劃多條符合飛行特性及機間關系的路線，該編隊路線在相應約束條件下達到最優或者接近最優效果。航跡規劃問題可以看作一個數學優化問題，即在一定約束條件下求解一個目標函數的最優值問題。因此，本文針對現有研究，從目標函數的構建以及模型求解算法兩個方面進行總結。

目標函數構建主要包括飛行器自身約束、航跡安全性、機間協調以及任務完成效果^［6］。飛行器自身約束指的是航線的實際可行性受到飛行器自身性能參數的限制，主要包括飛行時間、飛行高度、燃油消耗、動力學和位姿^［7-8］等。航跡安全性指的是飛行器在飛行過程中需避開或者盡可能在短時間通過威脅區域^［9-10］，威脅區域主要包括地形威脅以及藍方（進功方）威脅，其中雷達探測威脅是藍方進功方威脅的重要一環。目前，大多數研究是將單部雷達的探測區域作為一個獨立威脅區域，依據無人機與雷達之間的距離規定威脅成本^［11-13］，針對組網雷達探測威脅的研究較少。文獻［1］依據組網雷達探測特性計算組網雷達對編隊各航線節點的探測威力圖，然而其不能夠直觀地描述組網雷達探測威脅。機間協調指的是多架飛機間的空間和時間約束，主要包括避碰^［8］、同步性要求^［14］、連通性維護^［15］、編隊約束^［16］等。現階段針對多機伴隨式編隊機間協調的研究較少，由于多機伴隨式編隊由兩類飛機構成，其不僅需要考慮多架飛機間的空間和時間約束，還需要考慮干擾機群與目標機群間的關系。任務完成效果指的是不同應用場景下多機編隊所負責任務的完成情況，目的是引導多機編隊在有限的時間內完成任務并實現最大收益，例如在覆蓋搜索任務中往往以最大環境探索和覆蓋率描述任務完成效果^［17-18］。多機伴隨式編隊的主要任務是協同干擾組網雷達，因此協同干擾效果即為任務完成效果，合理描述協同干擾效果是多機伴隨式編隊航跡規劃準則的重要部分。

模型求解算法可以大致分為3類^［19］：精確方法、傳統啟發式算法和元啟發式算法^［20］。相對于元啟發式算法，一般將精確方法和傳統啟發式算法稱之為傳統方法，主要包括Dijkstra算法^［21］、A^*算法^［22-23］、快速搜索隨機樹算法^［24-25］以及模擬退火算法^［26］等。傳統方法雖然易于實現，但是缺乏靈活性，僅能在一些簡單場景中表現出良好性能。近年來，由于元啟發式算法在處理無人機約束方面的有效性以及在復雜場景中搜索全局最優的能力，其在航跡規劃中變得越來越流行，主要包括遺傳算法（genetic algorithm， GA）^［27-28］、蟻群優化（ant colony optimization， ACO）算法^［29-30］、粒子群優化（particle swarm optimization， PSO）算法^［31-32］、差分進化（differential evolution， DE）算法^［33］、螢火蟲算法（firefly algorithm， FA）^［34-35］、布谷鳥搜索（cuckoo search， CS）算法^［36］等。

在現有的元啟發式算法中，PSO算法具有群體智能的兩個重要屬性，即認知性和社會一致性，這些特性允許群中每個粒子遵循自己的經驗和群經驗來搜索解。與其他啟發式算法相比，PSO算法能夠在較短的計算時間內找到全局解，并具有穩定的收斂性^［37］，同時由于其群體性質，PSO算法可以并行運行在多個處理器上，節省航跡規劃所需的計算時間^［38］。鑒于上述優點，PSO算法被廣泛應用于航跡規劃問題，并產生了許多變體。文獻［39］提出一種無人機網絡分布式動態PSO算法，用于在災難場景中探測任務生成航跡;文獻［40］提出一種基于綜合改進PSO算法的無人機編隊三維航跡規劃算法，其中包括改進粒子的初始分布、自適應調整參數以及用期望粒子代替不期望粒子的變異策略;文獻［41］為解決傳統PSO算法容易早熟收斂導致陷入局部最小的問題，提出一種改進PSO算法，能夠更加快速、準確地規劃三維航跡;文獻［42］針對無人機在復雜環境中的航跡規劃問題，提出一種基于球面矢量的PSO算法，能夠生成高質量的解決方案。為提高多無人機協同系統的魯棒性和自適應性，分布式PSO算法被廣泛應用。文獻［43］受協同進化理論的啟發，提出一種具有精英保持策略的分布式協同PSO算法，該算法能夠滿足無人機間的協作要求和約束條件，與協同進化遺傳算法相比，有更好的穩定性和搜索成功率;文獻［44］針對不同的戰術需求，提出了3種基于分布式PSO的航跡規劃算法，能夠有效地為執行偵察任務的無人機群生成航跡。為進一步提高算法的性能，PSO算法常常與其他算法相結合，文獻［45］針對多無人機廣域最優覆蓋航跡規劃問題，提出一種基于PSO算法和GA的混合算法，綜合兩者優勢，能夠在合理的計算時間內獲得高質量解。文獻［46］針對PSO算法易于陷入局部最優和收斂速度慢的特點，設計一種改進PSO機制——空間細化投票機制（spatial refined voting mechanism， SRVM），提高所有粒子的搜索精度和速度。文獻［13］采用3種有效策略對PSO算法進行改進，并將改進PSO算法與改進共生有機體搜索（modified symbiotic organisms search， MSOS） 相結合，提出一種新的混合PSO算法，用于求解多無人機的協同航跡規劃問題，在收斂精度、收斂速度和穩定性方面具有顯著優勢，為進一步提高PSO算法的性能提供了思路。

總而言之，從上述不同場景的目標函數構建以及模型求解方法可以看出，針對多目標突防組網雷達場景的多機伴隨式編隊航跡規劃的研究較少。因此，本文主要在已有研究的基礎上，完成多機伴隨式編隊航跡規劃模型的構建，并提出一種有效的模型求解方法以進行求解。本文的主要工作可以總結如下：

（1） 從飛行器自身約束、航跡安全性、機間協調以及任務完成效果4個方面出發，結合多機伴隨式編隊及其所處環境特點，提出較為完備的航跡規劃準則，構建一個新的整體目標函數。

（2） 提出一種新的模型求解方法，稱為基于多球面矢量的逐航跡點學習混合PSO（multi-spherical vector-based hybrid PSO with track point by track point learning， MS-TLHPSO）算法。其中，所提出的MS方法使用兩類向量分別表示每架飛機的機動特性以及伴飛干擾機與目標飛機間的聯系，能夠有效提高算法搜索能力;所提出的TLHPSO算法避免了進化航跡點信息被掩蓋，同時提高了算法的探索和開發能力。

（3） 針對已構建的航跡規劃模型以及模型求解方法進行仿真實驗，并將所得結果與已有航跡規劃方法進行比較，驗證本文所提模型和方法的有效性。

1 多機伴隨式編隊航跡規劃模型

1.1 系統配置

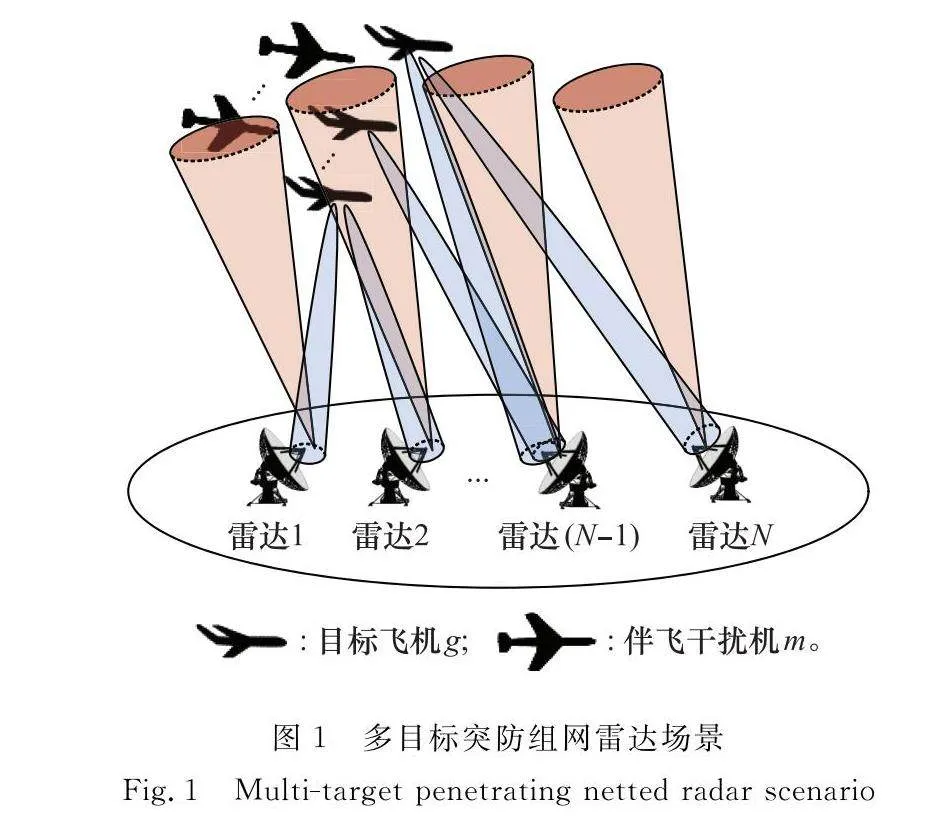
為有效描述多機伴隨式編隊突防組網雷達的組網過程，構建了多目標突防組網雷達場景，如圖1所示。其中，假設編隊中有多個目標飛機，干擾機在伴飛目標的同時對組網雷達進行協同干擾，降低組網雷達對目標飛機的檢測性能。

組網雷達由N部雷達組成，第n部雷達的坐標為R_n=（x_n，y_n，z_n），圖1中紅色波束表示組網雷達對多機伴隨式編隊的探測;多機伴隨式編隊由目標飛機和伴飛干擾機組成，目標飛機數為G，目標飛機g（g=1，2，…，G）在k時刻的航跡點為T^g_k=（x^g_k，y^g_k，z^g_k）;伴飛干擾機數為M，伴飛干擾機m（m=1，2，…，M）在k時刻的航跡點為T^m_k=（x^m_k，y^m_k，z^m_k）;各個干擾機中的干擾波束如圖1藍色波束所示，本文利用u_k和P_k對多波束干擾系統的波束指向以及發射功率進行描述：

u_k=［u¹_k，u²_k，…，u^M_k］^T（1）

P_k=［P¹_k，P²_k，…，P^M_k］^T（2）

式中：u^m_k=［u_m，1，k，u_m，2，k，…，u_m，N，k］^T表示干擾機m在k時刻的波束指向;P^m_k=［P_m，1，k，P_m，2，k，…，P_m，N，k］^T表示干擾機m在k時刻的波束發射功率。

1.2 目標函數構建

本節從飛行器自身約束、航跡安全性、機間協調以及任務完成效果4個方面出發，結合多機伴隨式編隊及其所處環境特點，提出較為完備的航跡規劃準則，構建整體目標函數。其中，航跡長度成本、高度成本以及平滑成本表示飛行器自身約束;雷達探測威脅成本表示航跡安全性;多機伴隨式編隊機間協調成本表示機間協調;協同干擾效果成本表示任務完成效果。

（1） 航跡長度成本

為使飛機在飛行過程中高效運行，同時資源利用更加合理，在優化準則中定義最小化航跡長度。首先得到K個航跡點的坐標T^a_k=（x^a_k，y^a_k，z^a_k），其次計算相鄰兩個航跡點之間的歐式距離T^a_kT^a_k+1，最終得到關于航跡長度的成本函數J₁：

J₁=∑Aa=1∑K-1k=1T^a_kT^a_k+1（3）

（2） 航跡高度成本

在飛行過程中，往往將飛行高度定義在執行相應任務的可行范圍內，從而得到與航跡點相關的高度成本H^a_k：

H^a_k=h^a_k－（h_max+h_min）2， h_min≤h^a_k≤h_max

∞， 其他

（4）

式中：h^a_k=z^a_k－h（x^a_k，y^a_k）表示k時刻航跡點z_k相對于地面h（x_k，y_k）的高度;h_min表示飛行高度設定最小值;h_max表示飛行高度設定最大值。

將各個航跡點的高度成本H_k進行累積求和，從而得到關于航跡高度的成本函數J₂：

J₂=∑Aa=1∑Kk=1H^a_k（5）

（3） 航跡平滑成本

航跡平滑成本用于評估各航跡點間轉彎速度以及爬升速度。

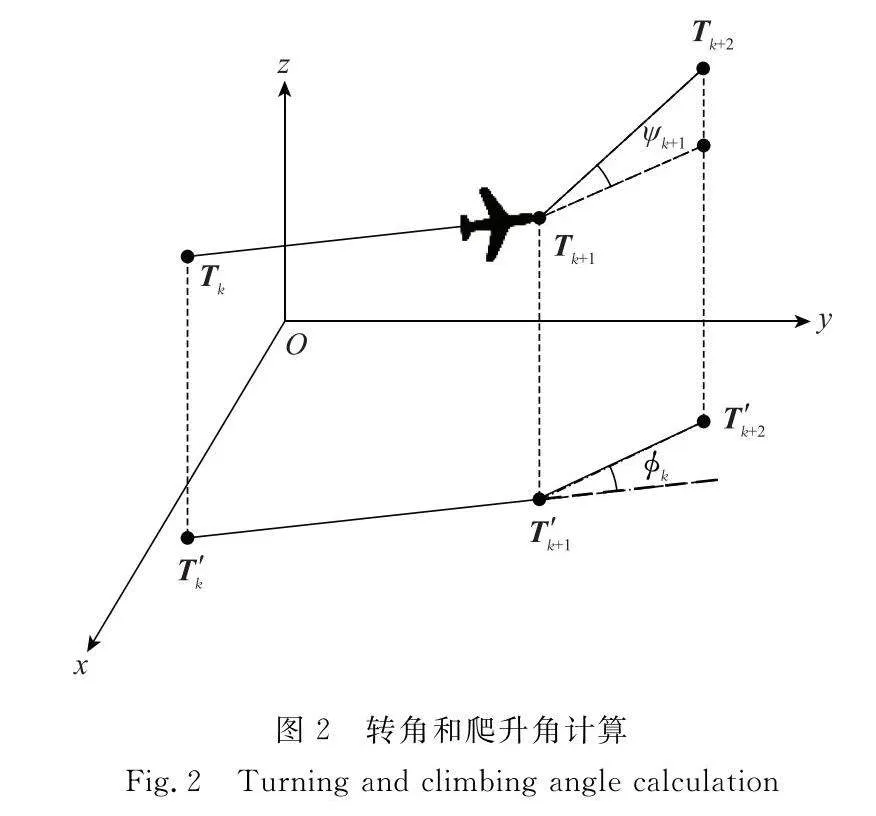
如圖2所示，轉角?_k表示兩條相鄰航跡T^a_kT^a_k+1和T^a_k+1T^a_k+2在Oxy平面的夾角：

?^a_k=arc tan

T^a_k′T^a_k+1′×T^a_k+1′T^a_k+2′T^a_k′T^a_k+1′·T^a_k+1′T^a_k+2′

（6）

式中：T^a_k′T^a_k+1′，T^a_k+1′T^a_k+2′表示T^a_kT^a_k+1和T^a_k+1T^a_k+2在Oxy平面的投影。

爬升角a_k表示相應航跡T^a_kT^a_k+1及其在Oxy平面的投影T^a_k′T^a_k+1′的夾角：

a_k=arctan

z^a_k+1－z^a_kT^a_k′T^a_k+1′（7）

式中：z^a_k表示飛機的z軸坐標，即該位置的地面高度加上飛行高度。

最終得到關于轉角和爬升角的成本函數J₃：

J₃=a₁∑Aa=1∑K－2k=1?^a_k+a₂∑Aa=1∑K－1k=1|a_k－a_k－1|（8）

式中：a₁，a₂分別表示轉角和爬升角的懲罰系數。

（4） 雷達探測威脅成本

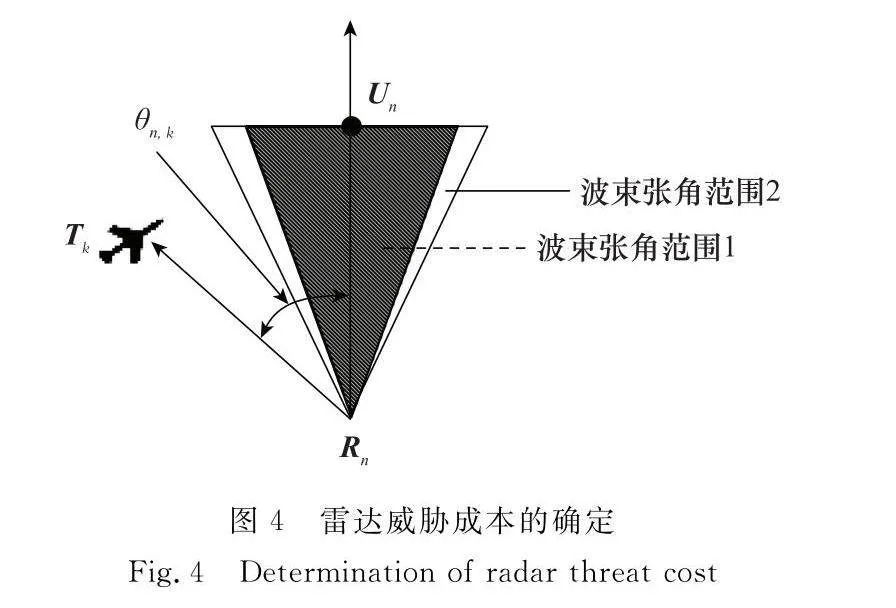
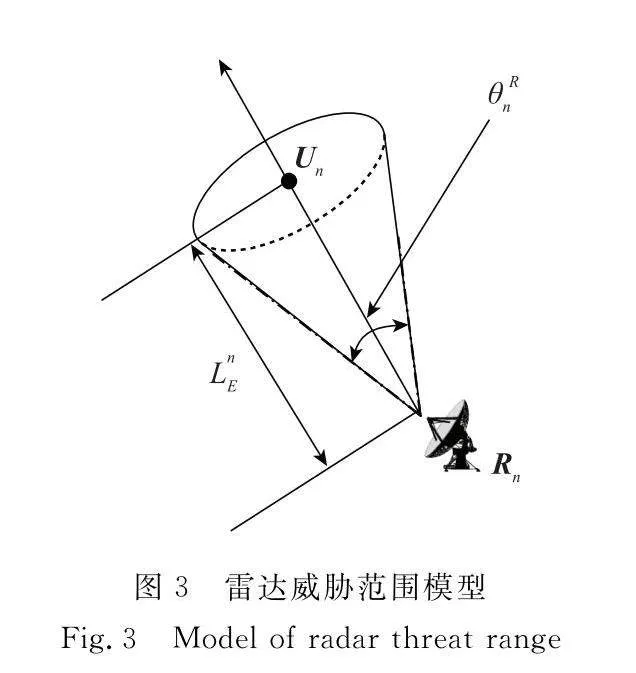
在多目標突防組網雷達場景中，為確保飛機在任務執行過程中的安全性，需要考慮組網雷達波束探測所帶來的威脅。因此，建立如圖3所示的雷達威脅范圍模型，假設已知N個雷達的波束指向R_nU_n、波束張角θ^R_n以及有效探測距離Lⁿ_E。

如圖4所示，為判斷航跡點T^a_k 是否在雷達威脅范圍內，需計算R_nU_n與R_nT^a_k的夾角θ^a_n，k，并將其與雷達波束張角范圍進行比較。

為更好確定關于雷達探測威脅所帶來的成本函數，將波束張角范圍設定為兩類。第一類為圖中陰影部分所示，波束張角θ^R_n與圖3構建模型一致，航跡點位于此范圍內，成本函數值設定為無窮大;第二類為圖中空白部分所示，其波束張角θ^RE_n=θ^R_n+θ_s。關于k時刻航跡點T^a_k 的成本函數C_n（T^a_k） 如下所示：

最終得到關于雷達探測威脅的成本函數J₄如下所示：

（5） 多機伴隨式編隊機間協調成本

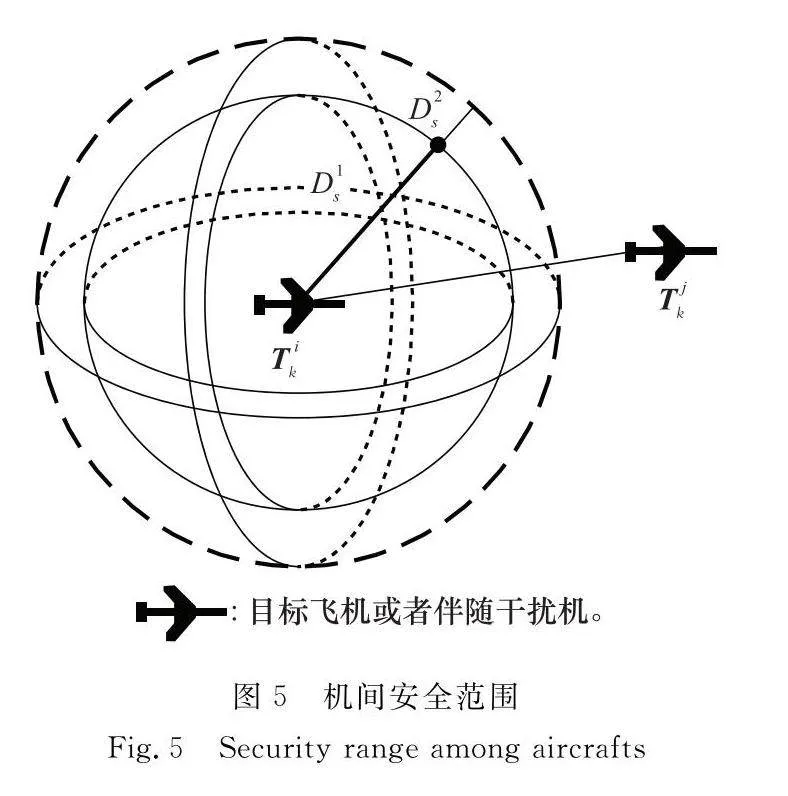
在多架飛機飛行過程中，首先需要考慮各飛機間避碰問題，假設每一架飛機的安全范圍如圖5所示，關于時刻航跡點T^a_k與T^b_k的機間碰撞成本函數AC（T^a_k，T^b_k）如下所示：

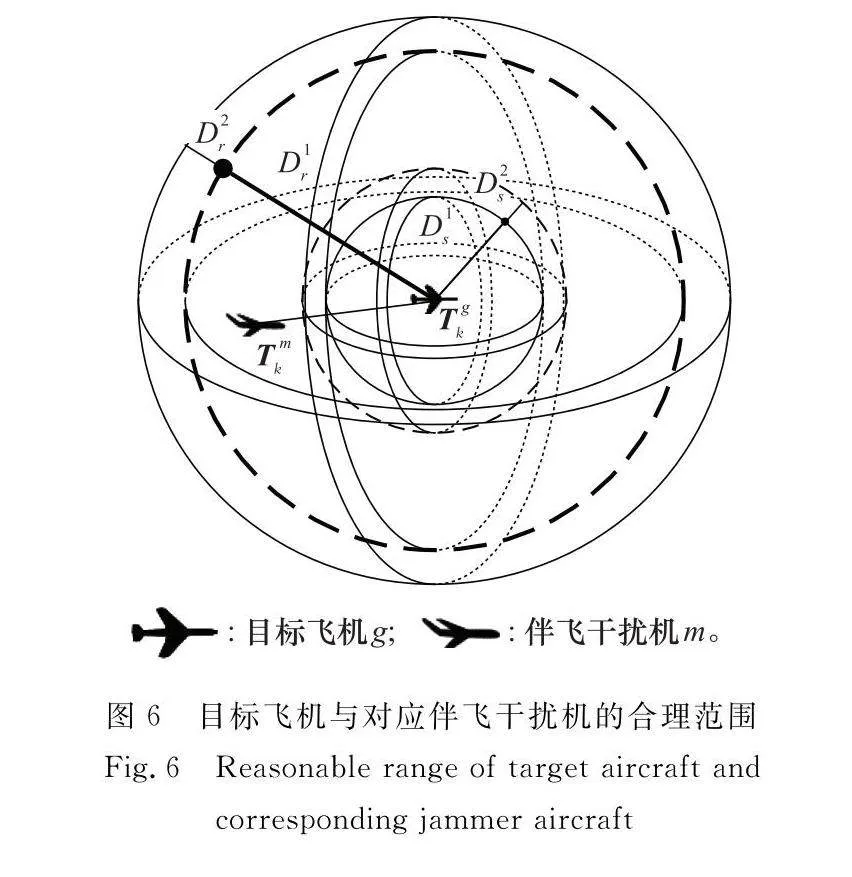
本文針對的是多目標突防組網雷達場景，因此在考慮機間協調成本時，需要保證目標飛機與其伴飛干擾機處于一個合理的范圍內。假設每一架目標飛機的合理范圍如圖6所示，關于k時刻目標飛機航跡點T^g_k與伴飛干擾機航跡點T^k_m的合理范圍成本函數AD（T^g_k，T^m_k）如下所示：

最終得到機間協調成本函數J₅如下所示：

J₅=a₃∑Aa=1∑Ab=a+1∑Kk=1AC（T^a_k，T^b_k）+

a₄∑Gg=1∑Mm=1，m∈Ug∑Kk=1AC（T^g_k，T^m_k）（14）

式中：a₃和a₄表示懲罰系數;U_g表示伴飛干擾機與目標飛機g相關聯的集合。

（6） 協同干擾效果成本

多機伴隨式編隊的主要任務是協同干擾組網雷達，因此協同干擾效果即為任務完成效果，合理描述協同干擾效果是多機伴隨式編隊航跡規劃準則的重要部分。考慮到壓制干擾的本質是將目標的回波信號湮沒在干擾信號中，以此來降低雷達對目標的檢測概率，同時檢測概率被眾多學者作為衡量干擾效果的指標，因此本文采用文獻［47］中基于檢測概率的協同干擾效果來評估指標。

首先得到k時刻雷達n對目標g的檢測概率^［48-50］：

Pd^g_n，k=e^{－VT1+SINRgn，k}（15）

式中：V_T為檢測門限值（多脈沖非相干積分的檢測閾值）;SINR^g_n，k表示在雷達n收到干擾時，目標飛機g的回波信干噪比。

其次，得到k時刻雷達n對目標飛機g的檢測概率：

Pd^g_k=∏Nn=1Pd^g_n，k（16）

最后，基于服務質量（quality of service， QoS）^［51］原理構建相應全局性能成本函數J₆：

式中：Pd^g_n，k（u_k，P_k）=［Pd¹_k，Pd²_k，…，Pd^G_k］為目標飛機檢測概率;［w¹_k，w²_k，…，w^G_k］表示目標飛機的檢測概率需求。

綜合上述飛行航跡規劃相應準則，本文構建整體目標函數如下所示：

min F=∑6i=1w_iJ_i（18）

式中：J_i表示飛行航跡規劃準則中對應的成本函數;w_i表示J_i對應的權重系數;該目標函數決策變量為G架目標飛機以及M架伴飛干擾機的所有航跡點T^a_k=（x^a_k，y^a_k，z^a_k）。

2 模型求解

隨著目標函數F的確定，多機伴隨式編隊航跡規劃問題可以轉化為數學優化問題，即確定決策變量最小化目標函數F。目標函數F通常是復雜的多峰函數，難以求得其最優解，因此本文針對多機伴隨式編隊特性，提出一種MS-TLHPSO算法，為航跡規劃提供高質量解決方案。

2.1 MS方法

文獻［42］利用飛機的機動特性，提出了基于球面矢量的PSO（spherical vector-based PSO， SPSO）算法，用以解決單架飛機航跡規劃問題。本文在此基礎上針對多機伴隨式編隊航跡特性，為有效描述每架飛機的機動特性以及伴飛干擾機與目標飛機間的聯系，提高算法搜索能力，提出MS方法。

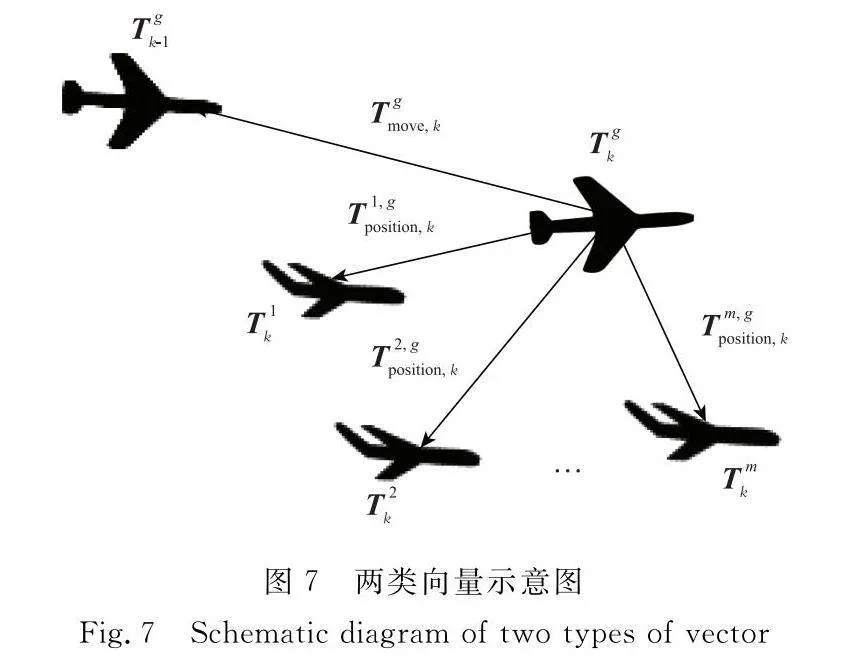
多機伴隨式編隊航跡規劃不僅需要考慮每架飛機的機動特性，還需要考慮伴飛干擾機與目標飛機間的聯系。因此，本文算法以每個目標飛機航跡點為中心給出兩類向量。如圖7所示，第一類向量V_move用于表示目標飛機從一個航跡點到下一個航跡點的移動，第二類向量V_position用于表示伴飛干擾機與其對應目標飛機間的相對位置。

圖7 兩類向量示意圖

Fig.7 Schematic diagram of two types of vector

為更直觀說明MS方法，本節將MS方法與PSO算法相結合進行說明，即基于多SPSO（multi SPSO， MSPSO）算法，該算法中一個粒子i的位置被描述為Ω_i，與粒子相關的速度則被描述為一個增量向量ΔΩ_i：

Ω_i=（V¹_move，i，…，V^G_move，i，V^1，1_position，i，…，V^M，G_position，i）（19）

ΔΩ_i=（ΔV¹_move，i，…，ΔV^G_move，i，ΔV^1，1_position，i，…，ΔV^M，G_position，i）（20）

式中：V^g_move，i表示目標飛機g的所有航跡點移動路線;V^m，g_position，i表示伴飛干擾機m與目標飛機g的相對位置：

V^g_move，i=

（ρ^g_i1，^g_i1，?^g_i1，ρ^g_i2，^g_i2，?^g_i2，…，ρ^g_i，K－2，^g_i，K－2，?^g_i，K－2）（21）

V^m，g_position，i=

（ρ^m，g_i1，^m，g_i1，?^m，g_i1，ρ^m，g_i2，^m，g_i2，?^m，g_i2，…，ρ^m，g_i，K－2，^m，g_i，K－2，?^m，g_i，K－2）（22）

將k時刻所有球面向量合集（ρ^all_ik，^all_ik，?^all_ik）表示為μ_ik;將速度（Δρ^all_ik，Δ^all_ik，Δ?^all_ik）表示為Δμ_ik，更新公式如下所示：

Δu^t+1_ik←

ωΔu^t_ik+c₁r_1k（q^t_ik－μ^t_ik）+c₂r_2k（q^t_gk－μ^t_ik）（23）

μ^t+1_ik←μ^t_ik+Δμ^t+1_ik，

i=1，2，…，I;k=1，2，…，K－2（24）

式中：ω為慣性權重;c₁c₂為學習因子;r_1k、r_2k均為［0，1］內的隨機數;Q_i=（q_i1，q_i2，…，q_i，K－2），Q_g=（q_g1，q_g2，…，q_g，K－2）分別表示粒子局部最佳位置和全局最佳位置的向量集。

為更好評估相應成本，以便確定粒子局部最佳位置和全局最佳位置，需要將Ω_i轉換為直接航跡點T_i：

x^g_ik=x^g_i，k－1+ρ^g_iksin ^g_ikcos ?^g_ik

y^g_ik=y^g_i，k－1+ρ^g_iksin ^g_iksin ?^g_ik

z^g_ik=z^g_i，k－1+ρ^g_ikcos ^g_ik

x^m_ik=x^g_i，k+ρ^m，g_iksin ^m，g_ikcos ?^m，g_ik

y^m_ik=y^g_i，k+ρ^m，g_iksin ^m，g_iksin ?^m，g_ik

z^m_ik=z^g_i，k+ρ^m，g_ikcos ^m，g_ik

（25）

局部最佳位置和全局最佳位置的更新如下所示：

Q_i（iter）=Ω_i， F（ξ（Ω_i））lt;F（ξ（Q_i（iter－1）））

Q_i（iter－1）， 其他（26）

Q_g=arg minQi F（ξ（Q_i））（27）

為進一步提高算法的探索和開發能力，進一步優化編隊航跡，本文對傳統PSO算法進行適應性改進。將在下一節介紹逐航跡點學習混合粒子群優化（hybrid pacticle swarm optimization with track point by track point learning， TLHPSO）算法。

2.2 TLHPSO算法

在多機伴隨式編隊軌跡規劃問題中，所求決策變量由路徑中各航跡點信息組成，因此為避免進化過程中航跡點信息間相互干擾導致正確信息被掩蓋的問題，本文提出一種逐航跡點學習策略，獨立地對每一航跡點信息進行考察;同時，與在多機航跡規劃問題上有較好表現的MSOS算法^［13］相混合，進一步提高算法探索和開發能力，最終形成TLHPSO算法。

本文算法動態改變慣性權重w、認知系數c₁以及社會系數c₂，使得搜索策略在不同階段受到不同因素影響：

w=w_max－t（w_max－w_min）/Ger

c₁=c_max－t（c_max－c_min）/Ger

c₂=c_min+t（c_max－c_min）/Ger（28）

式中：ω_max，ω_min表示慣性權重系數ω的最大值和最小值;c_max，c_min表示學習因子c₁和c₂的最大值和最小值;t表示當前迭代次數;Ger表示最大迭代次數。

本文算法在每一次迭代中，首先按照公式更新各個粒子位置及速度。其次，為更好挖掘局部最優解，引入MSOS算法。在此操作中，從粒子群中隨機選取一個Ω_j，并結合當前的全局最佳位置Q_g來得到個體Ω_i的新后代Ω_inew，Ω_j在同一時間執行相同的操作得到Ω_jnew，具體公式如下所示：

Ω_inew=Ω_i+r（Q_g－Ω_j）

Ω_jnew=Ω_j+r（Q_g－Ω_i）（29）

式中：r為［0，1］范圍內的隨機數。

再次，依據新個體Ω_inew和Ω_jnew更新個體Ω_i和Ω_j：

Ω_i=Ω_inew， F（ξ（Ω_inew））lt;F（ξ（Ω_i））

Ω_i， 其他 （30）

Ω_j=Ω_jnew，F（ξ（Ω_jnew））lt;F（ξ（Ω_j））

Ω_j，其他（31）

最后，按照式（26）和式（27）對局部最佳位置Q_i和全局最佳位置Q_g更新完畢后，引入Q_i指導Q_g的逐航跡點學習策略，該策略能夠避免進化航跡點信息被掩蓋的問題，提高求解質量。該策略思想為，依據每架飛機各個時刻航跡點分解位置向量Q_i和Q_g，將位置向量Q_i某一航跡點值替換Q_g對應航跡點值，形成新的位置向量newQ_g，并計算目標函數值，評價新的位置向量newQ_g，更新全局最佳位置Q_g：

Q_g=newQ_g， F（ξ（newQ_g））lt;F（ξ（Q_g））

Q， 其他（32）

當第i個粒子的局部最佳位置Q_i所有航跡點信息都對Q_g的對應維度指導完畢后，第（i+1）個粒子重復上述操作，直至所有粒子完成操作。

2.3 基于MS-TLHPSO求解多機伴隨式編隊航跡

首先，需要獲取目標組網雷達N個雷達節點的波束指向R_nU_n、波束張角θ^R_n以及有效探測距離Lⁿ_E;其次，需要設定整體目標函數相關參數;最后，基于MS-TLHPSO求解多機伴隨式編隊航跡。

具體步驟如算法1所示。

3 仿真實驗

本文仿真實驗處理器為Inter（R）Core（TM） i7-10875H CPU@2.30 GH。為更好地對本文算法性能進行分析，本節首先給出了實驗場景以及相關算法參數的通用設置;其次，本節在相同初始場景下進行實驗，從收斂曲線以及最優解兩個方面對算法尋優能力進行分析;最后，在不同初始場景以及航跡存在一定偏離的情況下進行實驗，進一步分析算法的穩定性。

3.1 實驗相關參數設置

假設組網雷達由N部雷達組成，伴飛干擾機數為M，目標飛機數為G，多波束干擾系統以及組網雷達相關參數參考文獻［47］。MS-TLHPSO算法相關參數設置如表1所示。

表1 MS-TLHPSO算法相關參數

Table 1 Parameters involved in MS-TLHPSO algorithm相關參數具體數值最大迭代次數Ger300粒子數I100慣性系數最大值W_max1慣性系數最小值W_min0.4學習因子最大值c_max2.5學習因子最小值c_min1.5評估周期T₁4逐航跡點學習周期T₂50

3.2 算法尋優能力分析

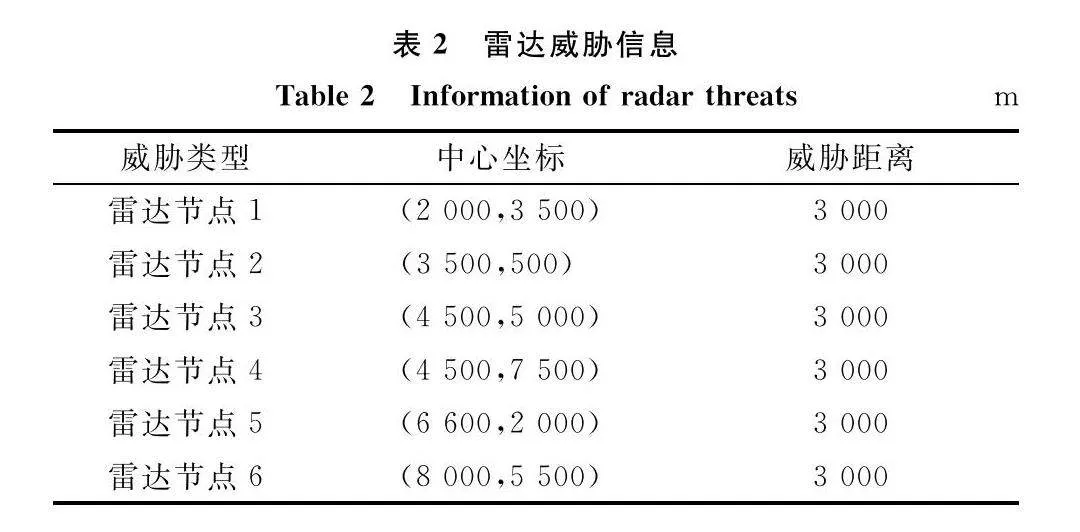
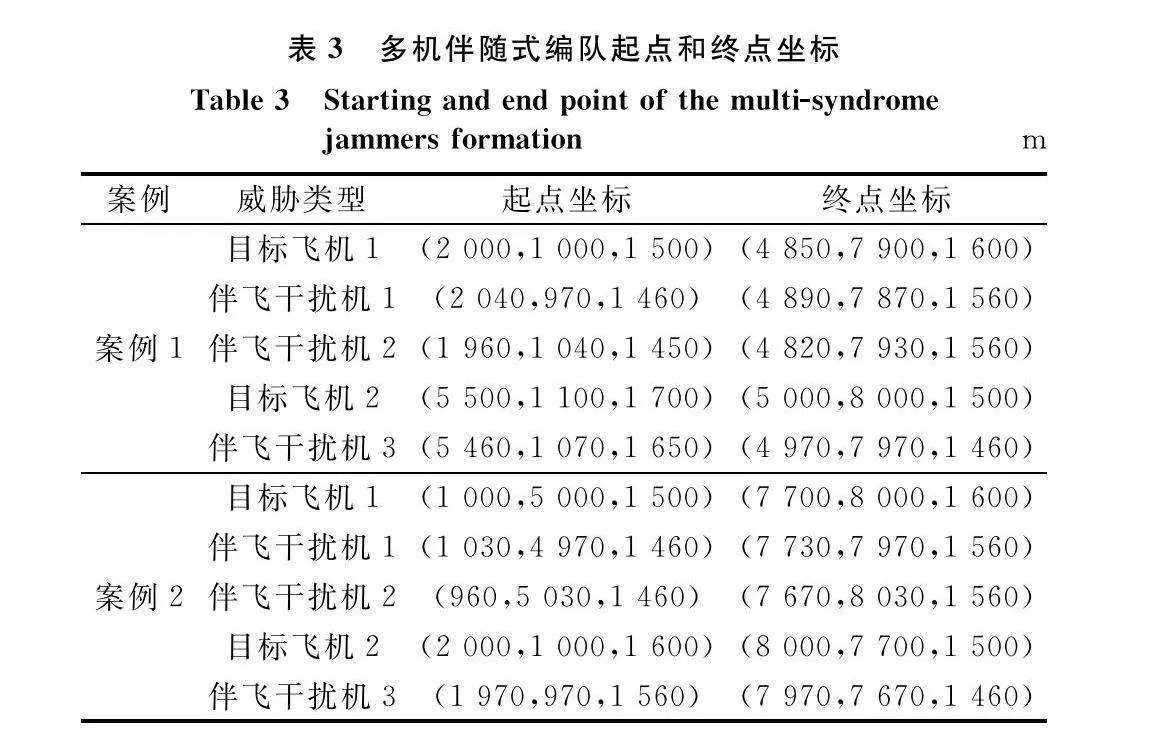
在本節中，為評估本文所提算法有效性以及尋優能力，在相同場景中模擬兩個不同案例進行實驗，兩個案例的起點和終點不相同，場景的初始條件以及兩個案例的具體設置如表2和表3所示。

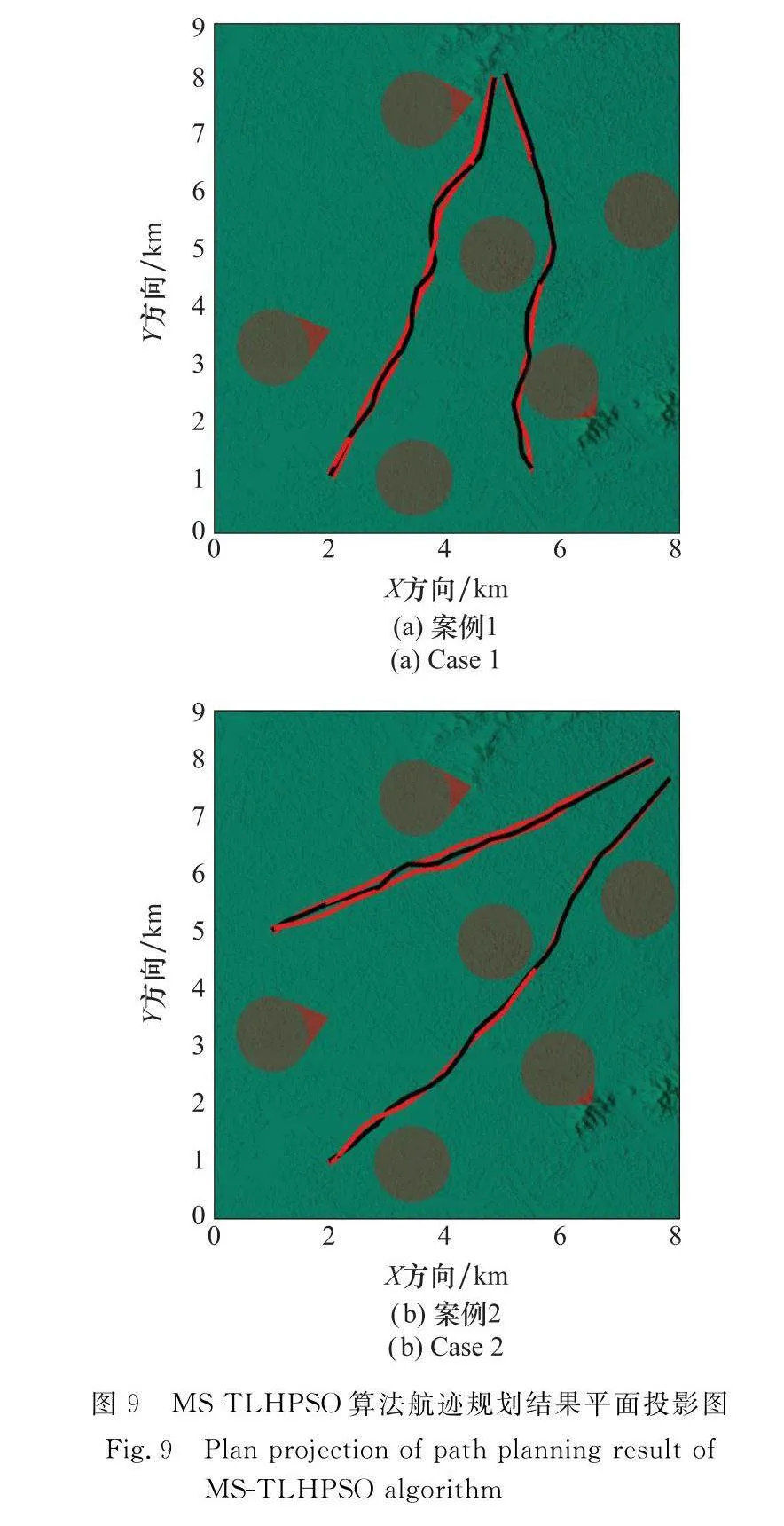
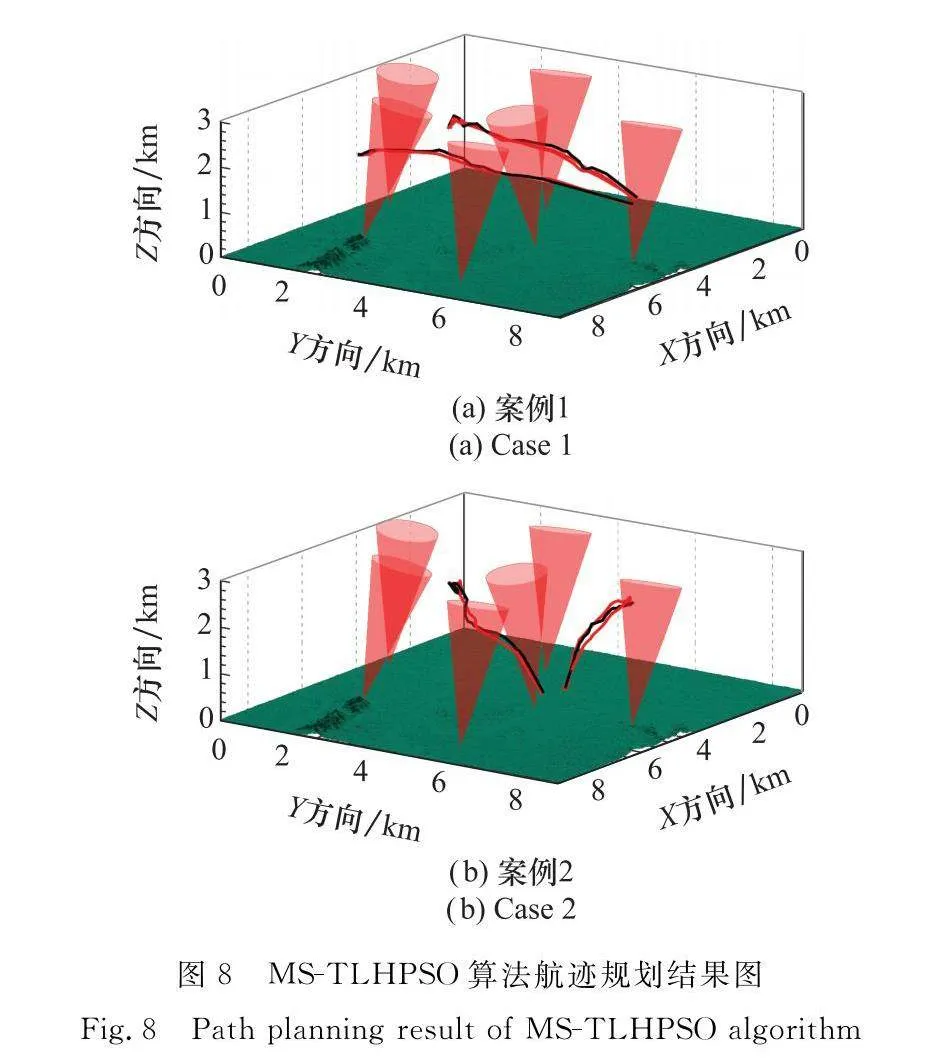
圖8為MS-TLHPSO算法航跡規劃結果圖，圖9為MS-TLHPSO算法航跡規劃結果平面投影圖。結合三維視圖以及平面投影圖可以看出，在兩個案例中，本文算法規劃結果均能夠滿足航跡規劃的預定要求，首先能夠有效規避雷達威脅，并對雷達節點實施干擾，保證航跡安全性;其次，能夠滿足已設定的機間合作約束，保證機間的合理安全距離和通信距離;最后，在保證安全性以及機間合作約束的前提下，最小化航跡的長度成本、高度成本以及平滑成本，更好地減少飛機的能源消耗。

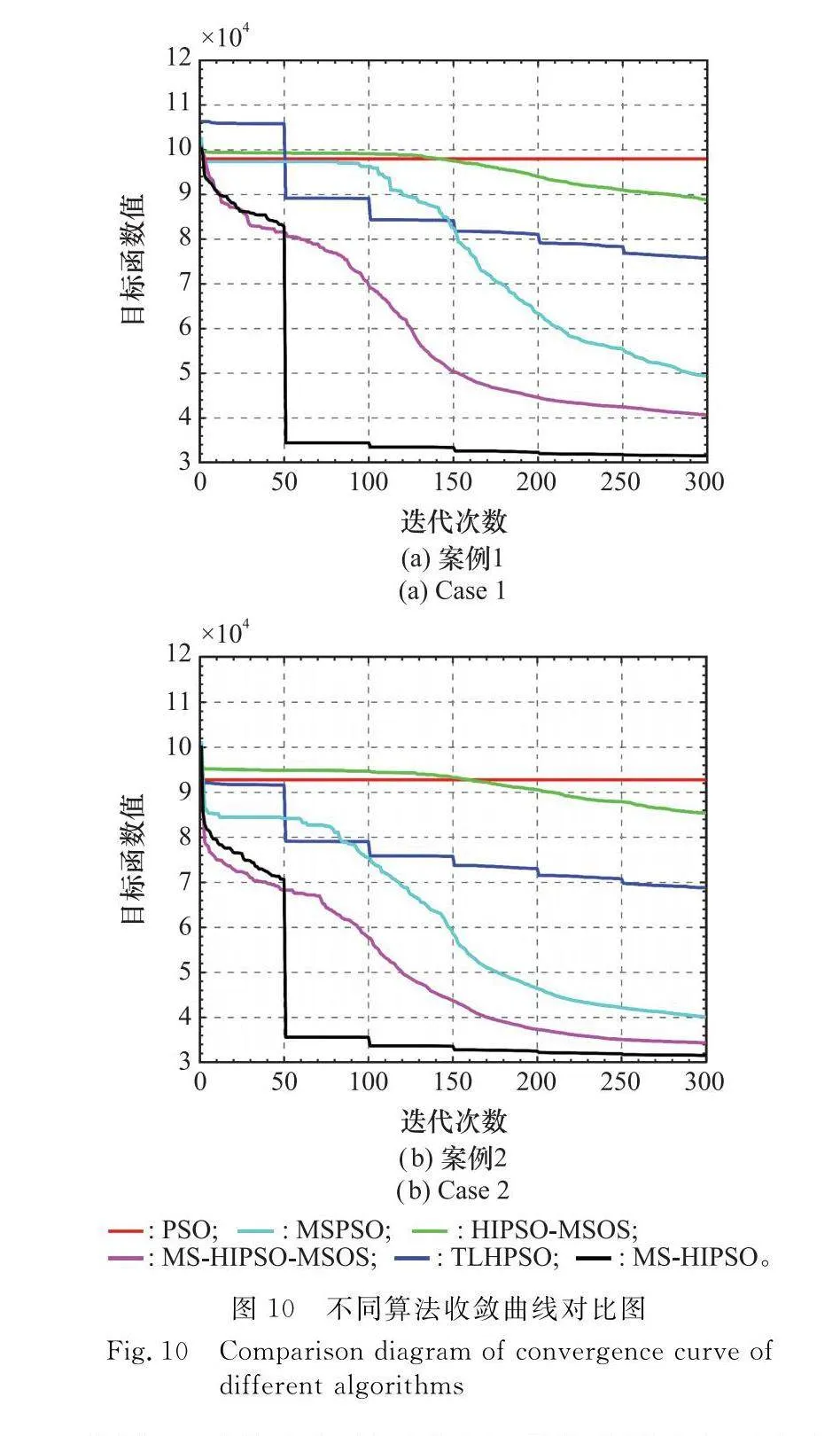
為進一步說明本文算法優勢，本節將6種算法應用至航跡規劃求解，并進行20組獨立實驗。其中，PSO算法為傳統PSO算法;混合改進粒子群優化改進共生有機體搜索（hybrid improved particle swarm optimization and modified symbiotic organisms search （HIPSO-MSOS）算法為文獻［13］所提算法;TLHPSO算法、多面球矢量粒子群優化（multi-spherical vector-based particle swarm optimization， MS-PSO）算法以及MS-TLHPSO算法為本文所提算法;MS-HIPSO-MSOS算法則由MS-PSO算法與HIPSO-MSOS算法相結合。各算法相關參數設置保持一致，圖10表示6種算法的收斂曲線（20組獨立實驗取平均值）。

從圖10可以看出，基于多MS的優化算法在兩個案例中效果明顯優于普通優化算法。分析原因，基于多MS的優化算法一方面利用向量V_move更好地描述目標飛機的機動特性，另一方面利用向量V_position描述伴飛干擾機與目標飛機間的聯系，能夠更加準確、有效地搜索最優編隊航跡，有效提高算法搜索能力。

TLHPSO算法在兩個案例中的效果明顯優于PSO算法和HIPSO-MSOS算法;同時MS-TLHPSO算法的效果也明顯優于MSPSO算法和MS-HIPSO-MSOS算法。分析原因，本文算法混合了MSOS算法，提高算法探索和開發能力，有利于挖掘最優解;同時設定周期為50的逐航跡點學習策略，能夠避免進化航跡點信息被掩蓋的問題，使得當周期為50時收斂曲線出現明顯下降，更好地跳出局部最優，獲得更優的編隊航跡。

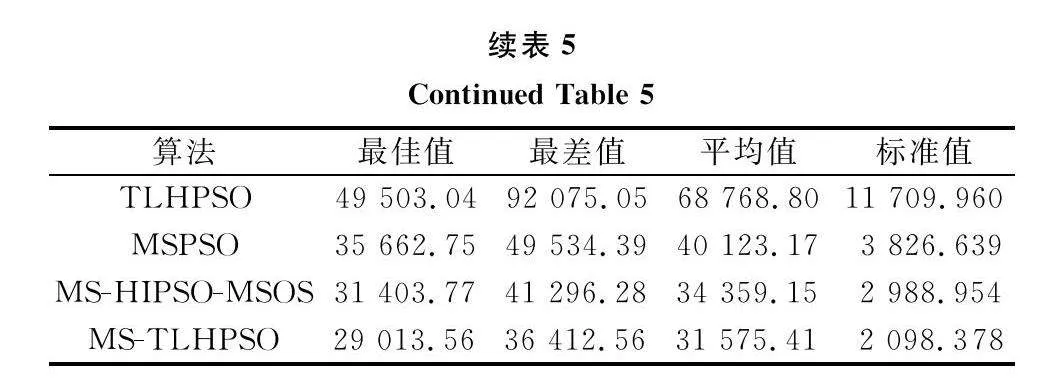
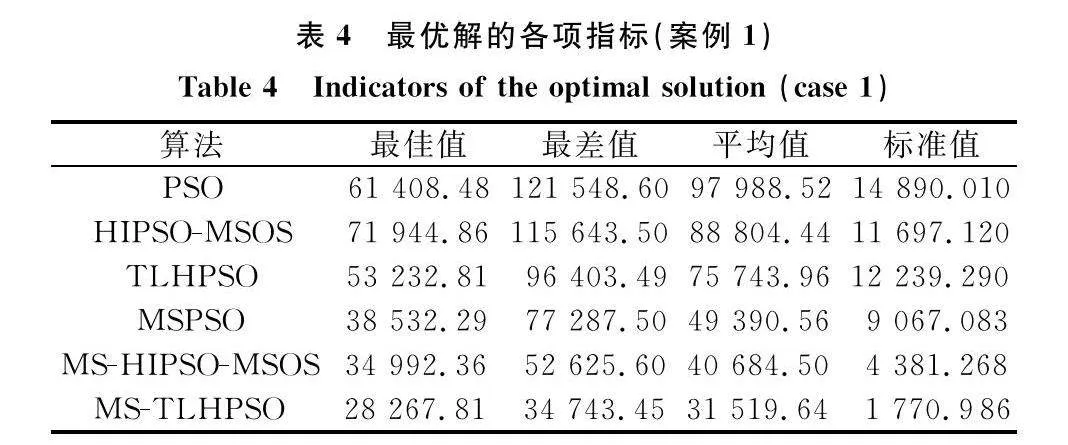
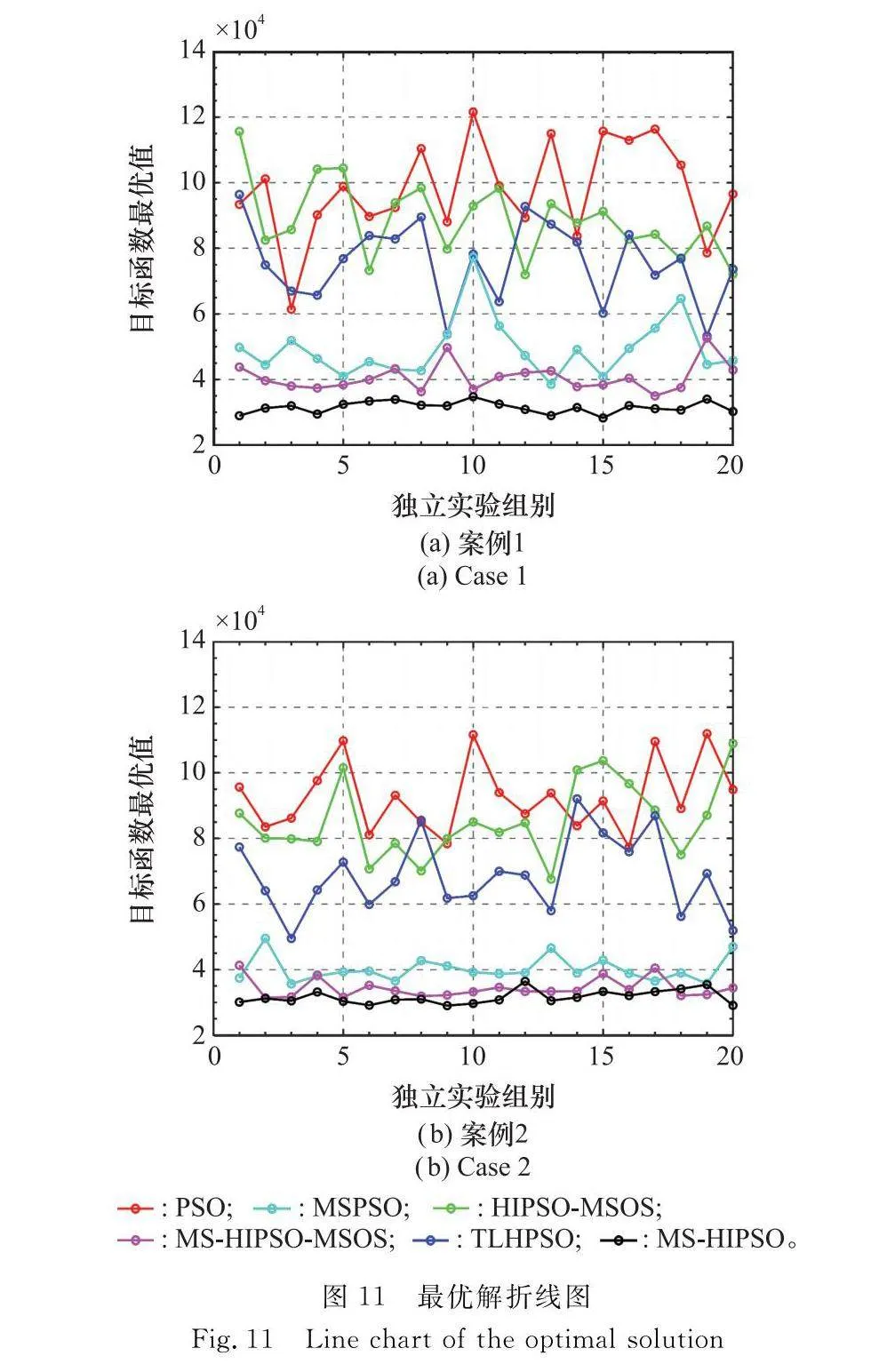
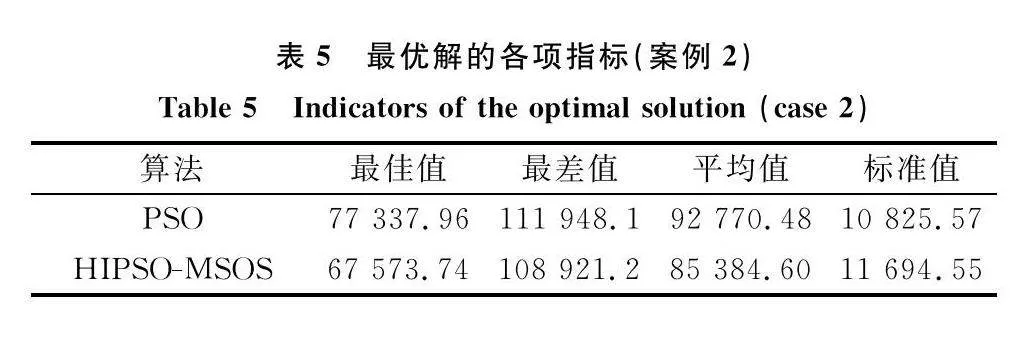
最后，針對不同獨立實驗中各算法最優解進行分析，圖11表示由20個獨立實驗中每個算法獲得的最優解組成的折線圖;表4和表5表示由20個獨立實驗中每個算法獲得的最優解的各項指標。

從圖11可以看出，在不同的案例中，本文所提MS-TLHPSO算法在絕大多數獨立實驗中，最優解值優于其他算法。從表4以及表5可以看出，在不同的案例中，本文所提MS-TLHPSO算法在最優解的最佳值、最差值、平均值以及標準差方面均優于其他算法。上述結果充分說明了本文算法的優勢，表明本文算法能夠在保證穩定性的前提下規劃具有更高可信度的編隊航跡。

3.3 算法穩定性分析

為進一步分析算法的穩定性，本節在不同的初始場景以及航跡存在一定偏離的情況下進行實驗。

（1） 不同初始場景的情況

本節首先引入不同初始場景，在第3.1節的基礎上加入了不同種類和不同數量的威脅，同時改變編隊飛機的組合和數量，在不同的對抗烈度情況下進行實驗。

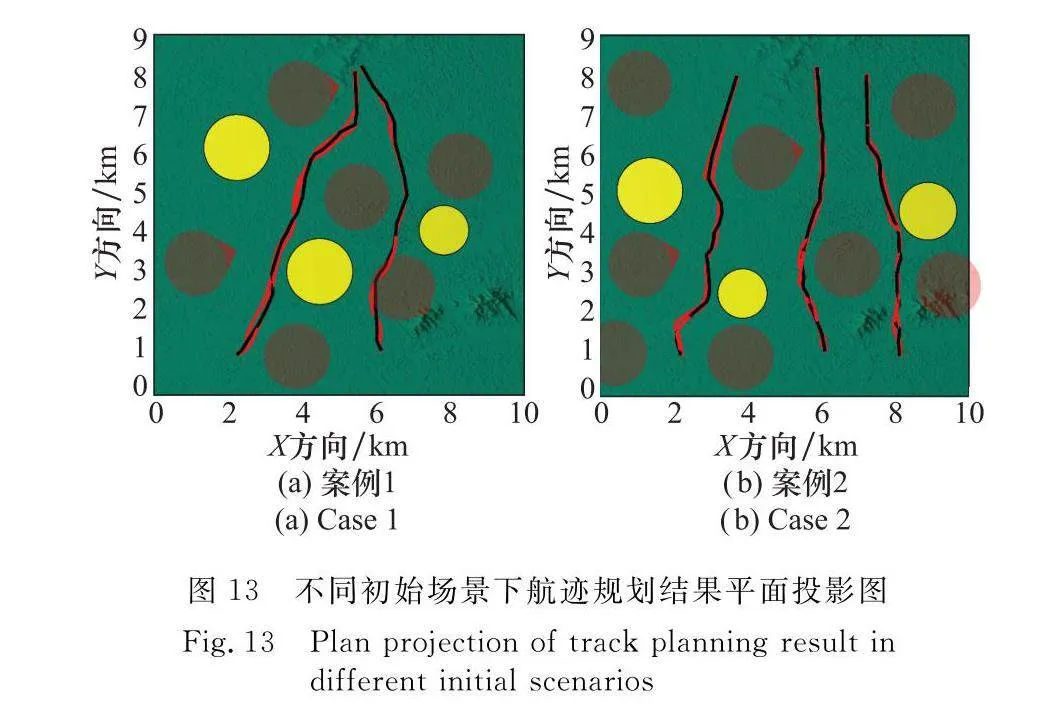
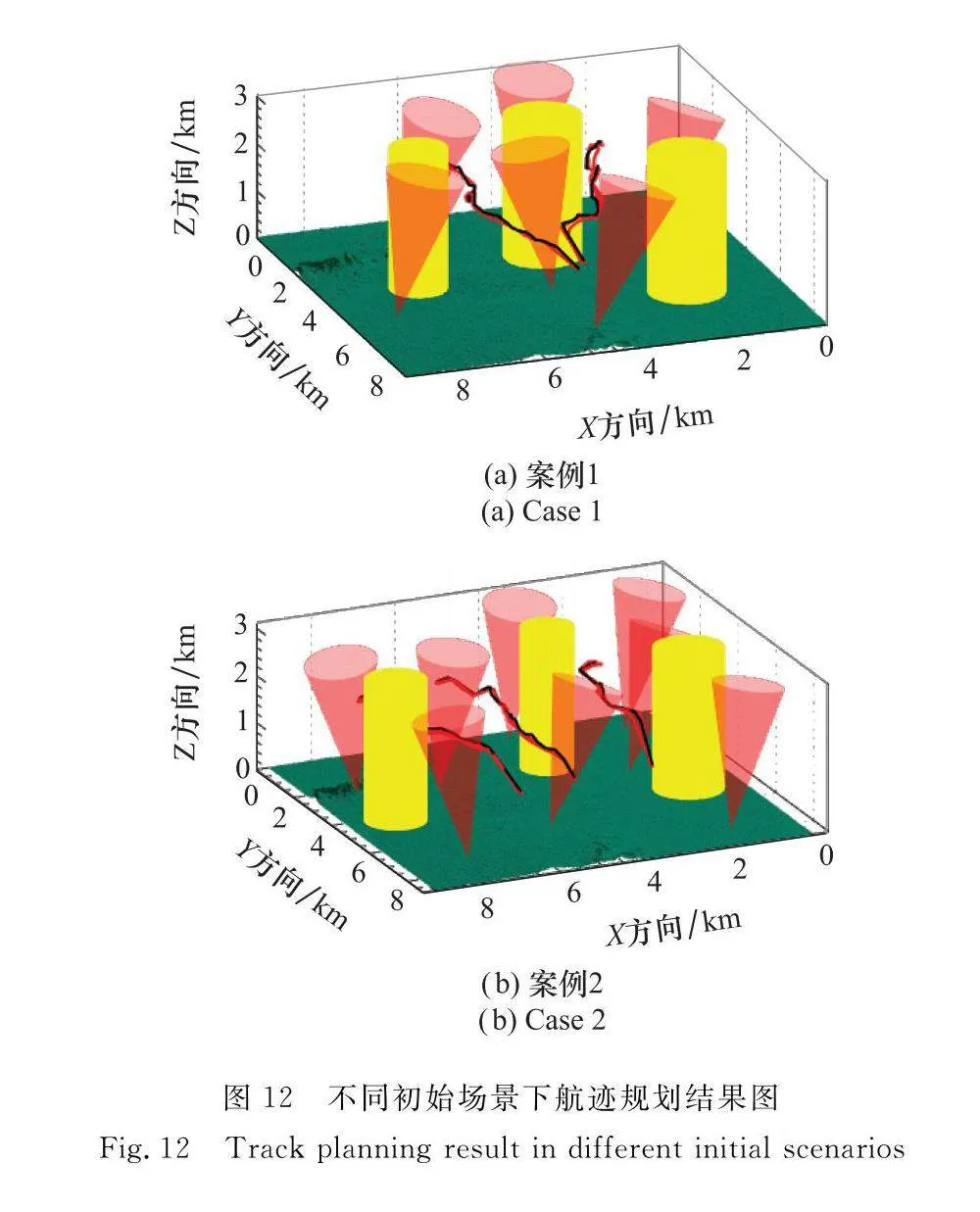
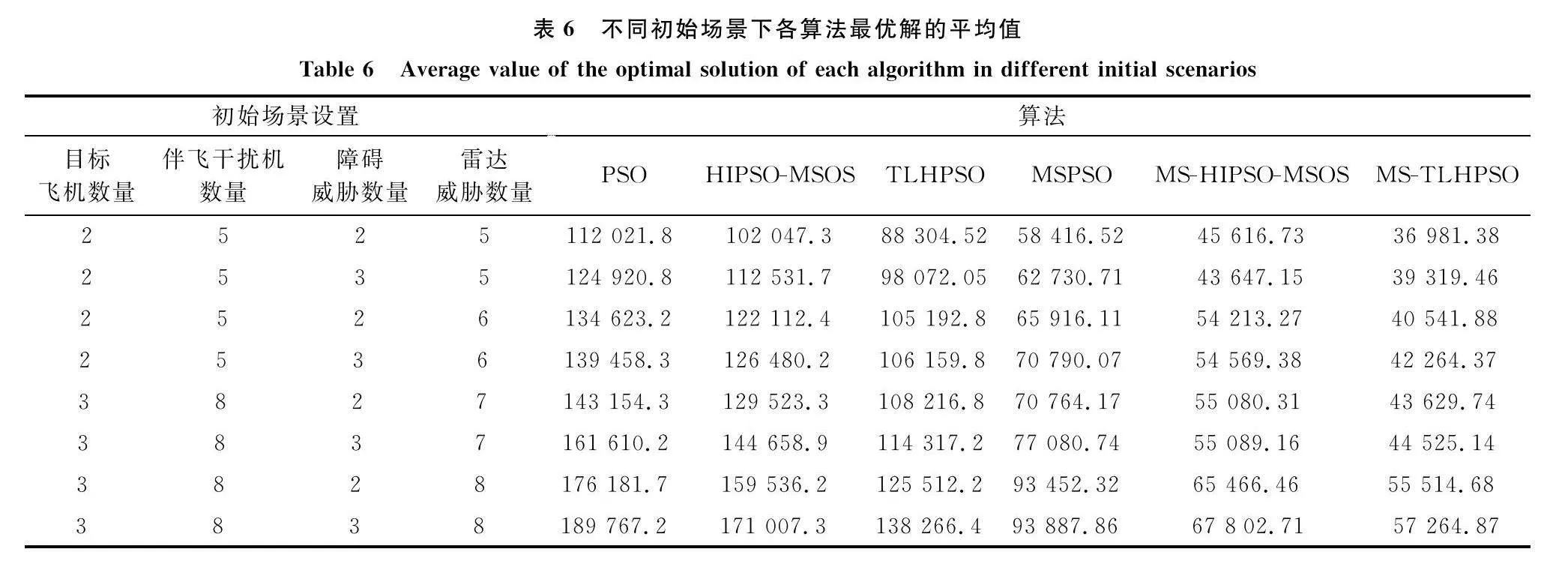
表6表示在8個不同對抗烈度下各個算法目標函數的最優解平均值比較結果（20組獨立實驗取平均）;圖12和圖13為兩個具有代表性案例的軌跡規劃結果圖（對應表6中第4種情況和第8種情況），圖中黃色圓柱體表示飛行過程中的障礙威脅，紅色波束表示飛行過程中的雷達威脅。

從圖12和圖13可以看出，在不同的初始場景下，本文算法規劃結果均能夠滿足航跡規劃的預定要求。從表6可以看出，在8種不同的情況下，本文算法的最優解平均值均優于其他對比算法，能夠有效說明本文所提算法的穩定性以及普遍適用性。

（2） 航跡存在一定偏離的情況

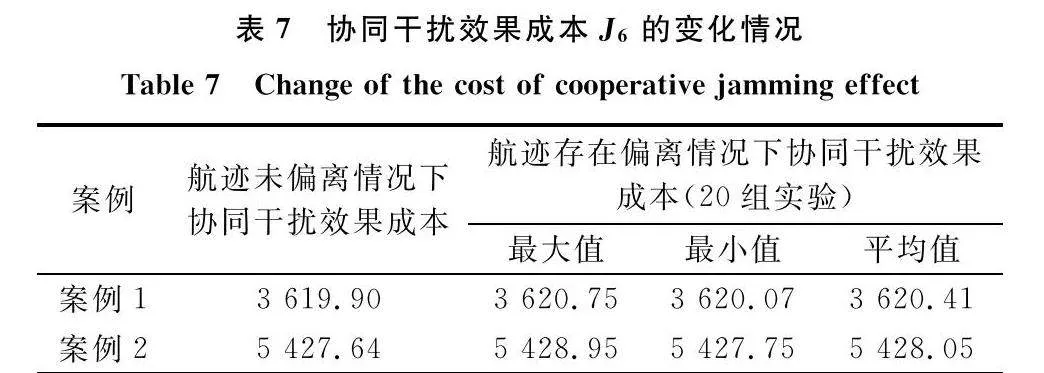
由于在飛行過程中存在多方面因素影響，航跡規劃結果可能存在一定的偏離情況。因此，本節在MS-TLHPSO算法航跡規劃結果中隨機加入一定程度的擾動，來觀察干擾效果的變化。

針對圖12中兩個案例的航跡規劃結果，對各個航跡點隨機加入擾動，并進行20次獨立實驗，得到協同干擾效果成本J₆的變化情況，如表7所示。

由表7可以看出，在本文算法規劃的航跡存在一定偏離的情況下，協同干擾效果成本函數值相較于未偏離情況有所上升，但是變化幅度并不明顯，說明本文算法所規劃的航跡結果在考慮擾動因素的情況下，依舊具有較好的穩定性。

4 結束語

本文有效完成了多目標突防組網雷達場景下編隊航跡規劃。首先，構建編隊航跡規劃模型，從飛行器自身約束、航跡安全性、機間協調以及任務完成效果4個方面出發，結合多機伴隨式編隊及其所處環境特點，提出較為完備的航跡規劃準則，形成一個新的整體目標函數，將航跡規劃問題轉化為數學優化問題。其次，為了更好地描述飛機的機動特性以及伴飛干擾機與目標飛機間的聯系，進一步提高算法的探索和開發能力，提出一種MS-TLHPSO算法以求解編隊航跡。最后，構建相應仿真場景進行驗證。實驗結果表明，本文所提算法能夠有效滿足編隊航跡規劃的預定要求，其中基于MS的方法性能明顯優于普通優化方法，TLHPSO算法性能明顯優于PSO算法和HIPSO-MSOS算法。同時，本文所提算法在最優解的最佳值、最差值、平均值以及標準差方面均優于其他算法，充分說明本文所提算法能夠在保證穩定性的前提下規劃具有更高可信度的編隊航跡，為進一步研究多機伴隨式編隊航跡規劃提供一些思路。

在多機伴隨式編隊航跡規劃研究領域，多目標優化算法的應用以及深度強化學習算法的應用可以作為未來的研究重點。針對多目標優化問題，本文采取的方法為對各優化目標函數添加相應的權重系數，將多目標問題轉化為單目標問題并進行優化處理，這種方法可能存在著權重系數設置不合理的情況，因此在未來的研究中，可以利用多目標優化算法解決此問題，為多機伴隨式編隊航跡規劃研究提供新思路。目前，本文所提方法僅適用于事先獲取戰場環境信息的情況，難以適用于動態場景。針對動態任務規劃場景，深度強化學習的應用是一個熱點領域。因此，下一步關于多機伴隨式編隊航跡規劃的研究應該更多關注基于深度強化學習算法的應用。

參考文獻

［1］張養瑞. 對組網雷達的多機伴隨式協同干擾技術研究［D］. 北京： 北京理工大學， 2015.

ZHANG Y R. Research on key technologies of cooperative ECM in multi-syndrome jammers for countering radar net［D］. Beijing： Beijing Institute of Technology， 2015.

［2］DENG C， WANG S W， HUANG Z， et al. Unmanned aerial vehicles for power line inspection： a cooperative way in platforms and communications［J］. Journal of Communications， 2014， 9（9）： 687-692.

［3］LEE K S， OVINIS M， NAGARAJAN T， et al. Autonomous patrol and surveillance system using unmanned aerial vehicles［C］∥Proc.of the IEEE 15th International Conference on Environment and Electrical Engineering， 2015： 1291-1297.

［4］SONG B D， PARK K， KIM J. Persistent UAV delivery logistics： MILP formulation and efficient heuristic［J］. Computers amp; Industrial Engineering， 2018， 120： 418-428.

［5］杜云， 賈慧敏， 邵士凱， 等. 面向多目標偵察任務的無人機航線規劃［J］. 控制與決策， 2021， 36（5）： 1191-1198.

DU Y， JIA H M， SHAO S K， et al. UAV trajectory planning for multi-target reconnaissance missions［J］. Control and Decision， 2021， 36（5）： 1191-1198.

［6］ZHANG H， XIN B， DOU L H， et al. A review of cooperative path planning of an unmanned aerial vehicle group［J］. Frontiers of Information Technology amp; Electronic Engineering， 2020， 21（12）： 1671-1694.

［7］CHEN Q Y， LU Y F， JIA G W， et al. Path planning for UAVs formation reconfiguration based on Dubins trajectory［J］. Journal of Central South University， 2018， 25（11）： 2664-2676.

［8］LIU Y， ZHANG X J， ZHANG Y， et al. Collision free 4D path planning for multiple UAVs based on spatial refined voting mechanism and PSO approach［J］. Chinese Journal of Aeronautics， 2019， 32（6）： 1504-1519.

［9］LIU W， ZHENG Z， CAI K Y. Distributed on-line path planner for multi-UAV coordination using bi-level programming［C］∥Proc.of the IEEE 25th Chinese Control and Decision Confe-rence， 2013： 5128-5133.

［10］BOUZID Y， BESTAOUI Y， SIGUERDIDJANE H. Guidance-control system of a quadrotor for optimal coverage in cluttered environment with a limited onboard energy： complete software［J］. Journal of Intelligent amp; Robotic Systems， 2019， 95（2）： 707-730.

［11］SHAO S， SHI W， ZHAO Y， et al. A new method of solving UAV trajectory planning under obstacles and multi-constraint［J］. IEEE Access， 2021， 9： 161161-161180.

［12］CHAI X Z， ZHENG Z S， XIAO J M， et al. Multi-strategy fusion differential evolution algorithm for UAV path planning in complex environment［J］. Aerospace Science and Technology， 2022， 121： 107287.

［13］HE W J， QI X G， LIU L F. A novel hybrid particle swarm optimization for multi-UAV cooperate path planning［J］. Applied Intelligence， 2021， 51（10）： 7350-7364.

［14］CHENG X M， CAO D， LI C T. Survey of cooperative path planning for multiple unmanned aerial vehicles［J］. Applied Mechanics and Materials， 2014， 668/669： 388-393.

［15］ZHANG D F， DUAN H B. Social-class pigeon-inspired optimization and time stamp segmentation for multi-UAV cooperative path planning［J］. Neurocomputing， 2018， 313： 229-246.

［16］WANG Z， LIU L， LONG T. Minimum-time trajectory planning for multi-unmanned-aerial-vehicle cooperation using sequential convex programming［J］. Journal of Guidance， Control， and Dynamics， 2017， 40（11）： 2976-2982.

［17］WU Q P， ZHOU S L， YAN S， et al. A cooperative region surveillance strategy for multiple UAVs［C］∥Proc.of the IEEE Chinese Guidance， Navigation and Control Conference， 2014： 1744-1748.

［18］ZHEN Z Y， XING D G， GAO C. Cooperative search-attack mission planning for multi-UAV based on intelligent self-organi-zed algorithm［J］. Aerospace Science and Technology， 2018， 76： 402-411.

［19］楊旭， 王銳， 張濤. 面向無人機集群路徑規劃的智能優化算法綜述［J］. 控制理論與應用， 2020， 37（11）： 2291-2302.

YANG X， WANG R， ZHANG T. Review of unmanned aerial vehicle swarm path planning based on intelligent optimization［J］. Control Theory amp; Applications， 2020， 37（11）： 2291-2302.

［20］趙暢， 劉允剛， 陳琳， 等. 面向元啟發式算法的多無人機路徑規劃現狀與展望［J］. 控制與決策， 2022， 37（5）： 1102-1115.

ZHAO C， LIU Y G， CHEN L， et al. Research and development trend of multi-UAV path planning based on metaheuristic algorithm［J］. Control and Decision， 2022， 37（5）： 1102-1115.

［21］程凝怡， 劉志乾， 李昱奇. 一種基于Dijkstra的多約束條件下智能飛行器航跡規劃算法［J］. 西北工業大學學報， 2020， 38（6）： 1284-1290.

CHENG N Y， LIU Z Q， LI Y Q. A Dijkstra based intelligent aircraft with multiple constraints track planning algorithm［J］. Journal of Northwestern Polytechnical University， 2020， 38（6）： 1284-1290.

［22］LIU X， GONG D X. A comparative study of A-star algorithms for search and rescue in perfect maze［C］∥Proc.of the IEEE International Conference on Electric Information and Control Engineering， 2011： 24-27.

［23］SONG R， LIU Y C， BUCKNALL R. Smoothed A* algorithm for practical unmanned surface vehicle path planning［J］. Applied Ocean Research， 2019， 83： 9-20.

［24］YERSHOVA A， JAILLET L， SIMéON T， et al. Dynamic-domain RRTs： efficient exploration by controlling the sampling domain［C］∥Proc.of the IEEE International Conference on Robotics and Automation， 2005： 3856-3861.

［25］SUN Q P， LI M， WANG T H， et al. UAV path plan-ning based on improved rapidly-exploring random tree［C］∥Proc.of the Chinese Control and Decision Conference， 2018： 6420-6424.

［26］BEHNCK L P， DOERING D， PEREIRA C E， et al. A modified simulated annealing algorithm for UAVs path planning［J］. IFAC-Papersonline， 2015， 48（10）： 63-68.

［27］ZENG X P， LI Y M， QIN J. A dynamic chain-like agent gene-tic algorithm for global numerical optimization and feature selec-tion［J］. Neurocomputing， 2009， 72（4-6）： 1214-1228.

［28］TSAI C C， HUANG H C， CHAN C K. Parallel elite genetic algorithm and its application to global path planning for autonomous robot navigation［J］. IEEE Trans.on Industrial Electro-nics， 2011， 58（10）： 4813-4821.

［29］ZHONG L， LUO Q， WEN D， et al. A task assignment algorithm for multiple aerial vehicles to attack targets with dynamic values［J］. IEEE Trans.on Intelligent Transportation Systems， 2013， 14（1）： 236-248.

［30］WU H S， LI H， XIAO R B， et al. Modeling and simulation of dynamic ant colony’s labor division for task allocation of UAV swarm［J］. Physica A： Statistical Mechanics and its Applications， 2018， 491： 127-141.

［31］CHEN D B， ZHAO C X. Particle swarm optimization based on endocrine regulation mechanism［J］. Control Theory and Applications， 2007， 24（6）： 126-134.

［32］ZHANG Q R， GU G C. Path planning based on improved binary particle swarm optimization algorithm［C］∥Proc.of the IEEE Conference on Robotics， Automation and Mechatronics， 2008： 462-466.

［33］ZHANG X Y， DUAN H B. An improved constrained differential evolution algorithm for unmanned aerial vehicle global route planning［J］. Applied Soft Computing， 2015， 26： 270-284.

［34］ALJARAH I， LUDWIG S A. A new clustering approach based on glowworm swarm optimization［C］∥Proc.of the IEEE Congress on Evolutionary Computation， 2013： 2642-2649.

［35］GOEL U， VARSHNEY S， JAIN A， et al. Three dimension path planning for UAVs in dynamic environment using glow-worm swarm optimization［J］. Procedia Computer Science， 2018， 133： 230-239.

［36］SONG P C， PAN J S， CHU S C. A parallel compact cuckoo search algorithm for three-dimensional path planning［J］. Applied Soft Computing， 2020， 94： 106443.

［37］GAING Z L. Particle swarm optimization to solving the economic dispatch considering the generator constraints［J］. IEEE Trans.on Power Systems， 2003， 18（3）： 1187-1195.

［38］LALWANI S， SHARMA H， SATAPATHY S C， et al. A survey on parallel particle swarm optimization algorithms［J］. Arabian Journal for Science and Engineering， 2019， 44（4）： 2899-2923.

［39］SANCHEZ-GARCIA J， REINA D G， TORAL S L. A distributed PSO-based exploration algorithm for a UAV network assisting a disaster scenario［J］. Future Generation Computer Systems—the International Journal of Escience， 2019， 90： 129-148.

［40］SHAO S K， PENG Y， HE C L， et al. Efficient path planning for UAV formation via comprehensively improved particle swarm optimization［J］. ISA Transactions， 2020， 97： 415-430.

［41］AHMED G， SHELTAMI T， MAHMOUD A， et al. IoD swarms collision avoidance via improved particle swarm optimization［J］. Transportation Research Part A： Policy and Practice， 2020， 142： 260-278.

［42］PHUNG M D， HA Q P. Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization［J］. Applied Soft Computing， 2021， 107： 107376.

［43］SHAO Z， YAN F， ZHOU Z， et al. Path planning for multi-UAV formation rendezvous based on distributed cooperative particle swarm optimization［J］. Applied Sciences， 2019， 9（13）： 2621.

［44］WANG Y B， BAI P， LIANG X L， et al. Reconnaissance mission conducted by UAV swarms based on distributed PSO path planning algorithms［J］. IEEE Access， 2019， 7： 105086-105099.

［45］HAGHIGHI H， SADATI S H， DEHGHAN S M M， et al. Hybrid form of particle swarm optimization and genetic algorithm for optimal path planning in coverage mission by cooperated unmanned aerial vehicles［J］. Journal of Aerospace Technology and Management， 2020， 12： e4320.

［46］LIU Y， ZHANG X J， ZHANG Y， et al. Collision free 4D path planning for multiple UAVs based on spatial refined voting mechanism and PSO approach［J］. Chinese Journal of Aeronautics， 2019， 32（6）： 1504-1519.

［47］張大琳， 易偉， 孔令講. 面向組網雷達干擾任務的多干擾機資源聯合優化分配方法［J］. 雷達學報， 2021， 10（4）： 595-606.

ZHANG D L， YI W， KONG L J. Optimal joint allocation of multi jammer resources for jamming netted radar system［J］. Journal of Radars， 2021， 10（4）： 595-606.

［48］DAUM F. Radar handbook［J］. IEEE Aerospace and Electronic Systems Magazine， 2008， 23（5）： 41.

［49］LIU W， WANG Y L， LIU J， et al. Performance analysis of adaptive detectors for point targets in subspace interference and Gaussian noise［J］. IEEE Trans.on Aerospace and Electronic Systems， 2018， 54（1）： 429-441.

［50］FANG Z X， WEI Z Q， CHEN X， et al. Stochastic geometry for automotive radar interference with RCS characteristics［J］. IEEE Wireless Communications Letters， 2020， 9（11）： 1817-1820.

［51］YI W， YUAN Y， HOSEINNEZHAD R， et al. Resource scheduling for distributed multi-target tracking in netted colocated MIMO radar systems［J］. IEEE Trans.on Signal Processing， 2020， 68： 1602-1617.

作者簡介

鄒瑋琦（1998—），男，碩士研究生，主要研究方向為認知干擾決策、協同干擾決策。

牛朝陽（1981—），男，副教授，博士，主要研究方向為雷達信息處理與對抗。

劉 偉（1980—），男，副教授，博士，主要研究方向為智能信息處理、遙感圖像分析。

王艷云（1998—），男，碩士研究生，主要研究方向為微波光子雷達。

湛嘉祺（1999—），男，碩士研究生，主要研究方向為無人機任務規劃。