基于目標量測誤差分布的航跡抗差關聯算法
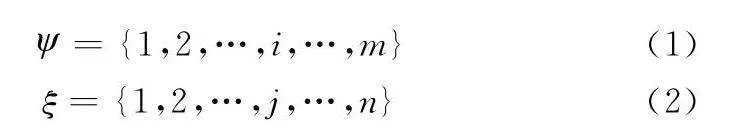
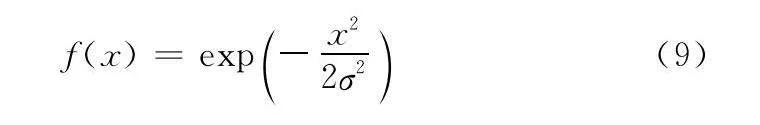
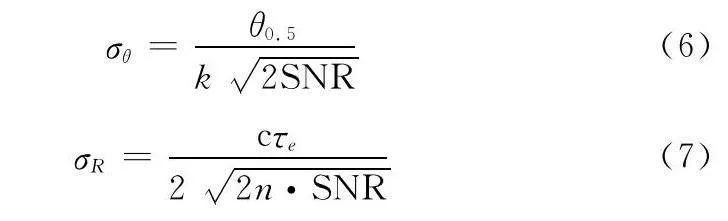
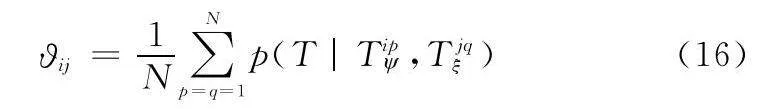


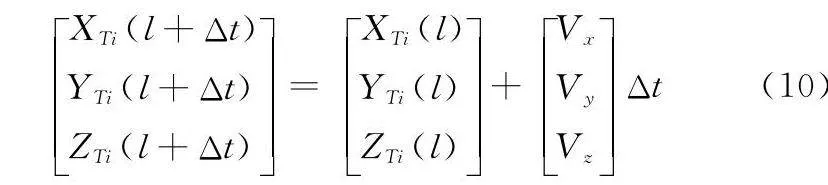
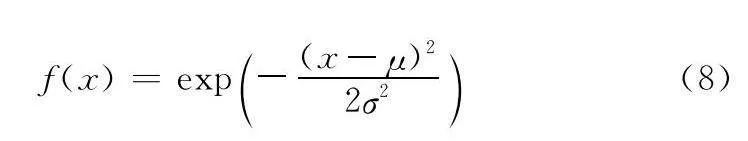
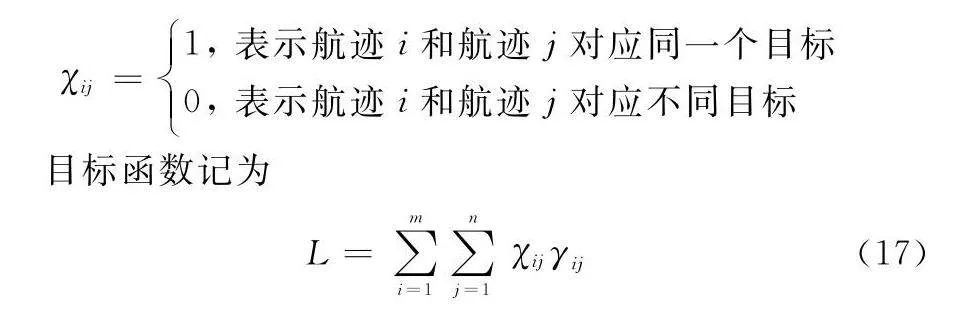
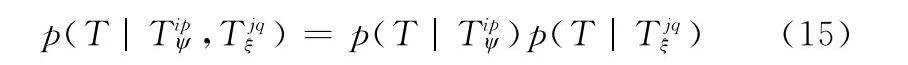
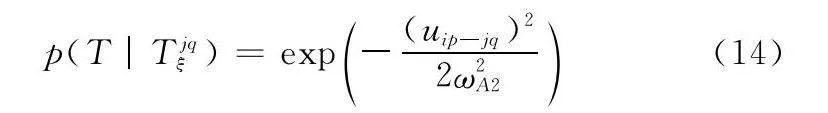
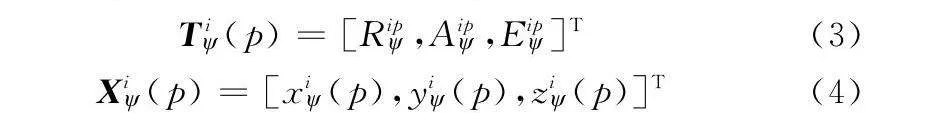
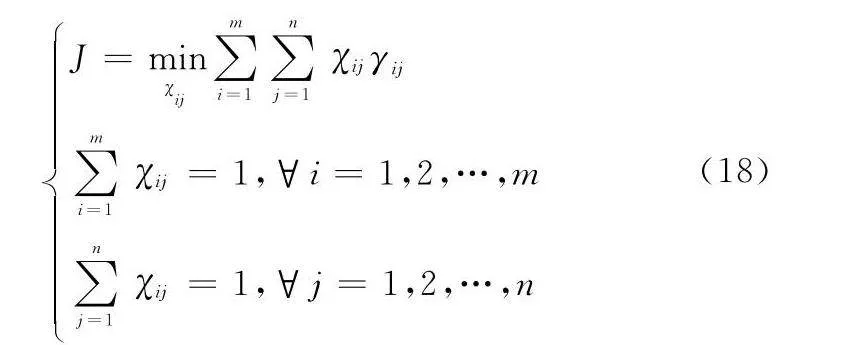

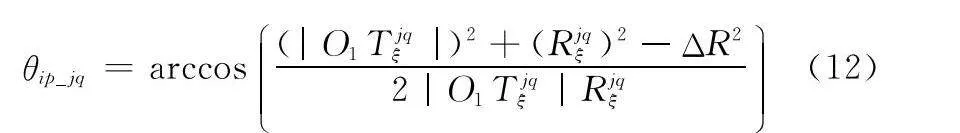
摘 要: 針對在遠距離密集目標情況下,因角度維誤差導致目標空間定位誤差變大而航跡誤關聯率較高的問題,提出一種基于目標量測誤差分布的航跡抗差關聯算法。首先在分析目標量測誤差空間概率分布特征的基礎上,定義了與目標同一性密切相關的視同因子;然后利用關聯目標對與雷達之間的幾何關系、目標量測距離和雷達站址等先驗信息,基于模糊數學理論中的高斯隸屬度函數,計算得到目標航跡之間的航跡關聯度和航跡關聯代價矩陣;最后利用經典分配法進行航跡關聯判定。仿真結果表明,所提算法航跡誤關聯率低、抗差性好,且不受目標數目變化的影響。
關鍵詞: 航跡關聯; 誤差分布; 隸屬度函數; 多維分配
中圖分類號: TN 957.51
文獻標志碼: A
DOI:10.12305/j.issn.1001-506X.2024.08.29
Anti-bias track association algorithm based on target measurement
error distribution
YANG Xin*, RUAN Kaizhi, LIU Hongming, WANG Xiaoke, LIU Jingqiu, SHI Yusheng
(Shanghai Electro-Mechanical Engineering Institute, Shanghai 201109, China)
Abstract: In the case of long-range and dense targets, aiming at the problem of high track error correlation rate due to large spatial positioning error of target caused by angle dimension error, an anti-bias track association algorithm based on target measurement error distribution is proposed. Firstly, based on the analysis of the spatial probability distribution characteristics of the target measurement error, the algorithm defines the reckon factor closely related to target identity. Then, using the geometric relationship between the associated target pair and radar, the measurement distance of target, the radar site and other prior information, the track association degree and track association cost matrices between the target tracks are calculated based on the Gaussian affiliation function in fuzzy mathematics theory. Finally, the classical allocation method is used to determine the track correlation. Simulation results show that the proposed algorithm has low track error correlation rate and good robustness, and is not affected by the number of targets.
Keywords: track association; error distribution; affiliation function; multidimensional allocation
0 引 言
在分布式多傳感器多目標跟蹤融合系統中,需要判斷不同傳感器上報的目標航跡是否源于同一目標,即航跡關聯[1-3]。航跡關聯是目標信息融合的前提,也是融合中心亟需解決的關鍵問題之一[4-6]。同時,隨著軍事技術的快速發展,采用分布式雷達組網對目標進行協同探測和戰場態勢監視已成為一種必然趨勢,多傳感器航跡關聯則顯得尤其重要[7-9]。但各傳感器采樣周期不一致和開機時間不同,致使局部節點上報目標航跡異步,系統誤差與隨機誤差的存在也導致目標觀測位置發生偏移且帶有誤差,這些都大大增加了航跡關聯的難度[10-27]。
其中,為克服系統誤差和隨機誤差對航跡關聯的影響,文獻[14-15]將系統誤差轉換為旋轉量和平移量,分別提出一種基于Fourier變換和Radon變換的航跡對準關聯技術,但在大系統誤差下,算法的抗差性較差。而文獻[16]采用基于密度的模糊聚類思想,將誤差帶來的不確定性模糊化,所提方法的關聯結果接近貝葉斯最小均方誤差準則下的結果。考慮系統誤差隨時間變化,文獻[17]用區間灰數來表示目標定位的不確定性,提出一種基于區間相離度的航跡灰色關聯算法。文獻[18-19]同樣使用灰色關聯理論,將時變系統誤差的影響用灰區域來描述,分別用灰色區間相對支持度和區域覆蓋度來表征目標航跡關聯程度的大小。但由于文獻[17-19]在計算航跡灰關聯系數時,各傳感器數據存在不可交換性,當存在非共同觀測目標時,航跡誤關聯率變大,故文獻[20]對灰關聯度進行修正并引入了目標航跡歷史信息,提出一種基于序貫修正灰關聯度的全局最優航跡關聯算法,提高了局部節點在非共同觀測目標情況下的航跡正確關聯率。
雖然各傳感器系統誤差的存在使目標航跡發生偏移,但對目標間的相對位置關系影響卻很小,故文獻[21]利用目標間恒定的相對距離信息,將拓撲結構相似性引入到航跡關聯中;文獻[22]基于量測目標拓撲結構的空間不變性,根據目標參照系下鄰近目標間的拓撲統計距離信息進行全局最優關聯;文獻[23]則采用參考拓撲特征表示航跡的不確定性,通過非剛性變換描述航跡間的結構差異;文獻[24]結合海上目標位置變化慢、空間拓撲關系穩定的特點,基于三角形穩定結構設計了適用于海上目標的航跡抗差關聯算法。不足的是,在目標密集分布情況下,此類算法的關聯計算量較大,且會導致目標空間拓撲關系不穩定,部分目標航跡被錯誤關聯,尤其是當目標位于遠距離時,由于測角誤差導致目標在角度維的定位誤差變大,這一現象更加明顯。
進一步,針對航跡異步、系統誤差與隨機誤差并存時的航跡關聯問題,文獻[25]基于高斯隨機矢量統計特性推導出一種基于距離分級聚類的機載雷達航跡抗差關聯算法,但測角隨機誤差的增大會導致關聯性能惡化。文獻[26]分析目標航跡間的時空交叉關系,定義廣義時空交叉點,提出了一種以航跡對時空交叉點為特征,通過特征匹配來實現航跡關聯的算法。文獻[27]則通過計算目標航跡序列與航跡點之間的k近鄰平均距離,進而用得到的不等長航跡序列之間的灰色關聯度,表征目標航跡之間的相似度,最后通過經典分配法進行異步航跡關聯判決,算法關聯效果較好。但以上算法仍然依賴于目標的空間定位精度,在距離遠、目標分布密集、系統誤差和隨機誤差較大條件下,航跡誤關聯率較高,算法抗差性較差。
針對以上問題,本文首先對航跡關聯問題進行描述,分析目標量測誤差空間的概率分布特征,給出利用目標量測距離信息進行目標關聯的基本思想,最后提出一種基于目標量測誤差分布的航跡抗差關聯算法。
1 問題描述
這里以兩部獨立的單基地雷達對同一遠距離空域內的多個目標進行監視和跟蹤為例,目標在所監視的空域內隨機分布,雷達1位于(L1,B1,H1),雷達2位于(L2,B2,H2),雷達數據融合中心位于(L0,B0,H0)。在某一時刻t,融合中心則會接收兩雷達局部節點上報的目標航跡信息。在融合中心的一個處理周期T內,可將兩雷達觀測得到的目標航跡標號集合記為
={1,2,…,i,…,m}(1)
ξ={1,2,…,j,…,n}(2)
式中:m和n分別表示雷達1和雷達2上報的目標航跡數;i和j對應不同目標的航跡序號。
在以雷達1站址為原點的北天東坐標系下,觀測目標航跡i的第p個航跡點的極坐標與北天東直角坐標為
Ti(p)=[Rip,Aip,Eip]T(3)
Xi(p)=[xi(p),yi(p),zi(p)]T(4)
式中:p=1,2,…,ni,ni表示雷達1采集的第i條航跡的航跡點數。
同理,對雷達2來說,觀測目標航跡ξj的第q個航跡點的極坐標與北天東直角坐標為Tjξ(q)和Xjξ(q),q=1,2,…,njξ,niξ表示雷達2采集的第j條航跡的航跡點數。此外,由于不同雷達傳感器的掃描周期不同,各雷達目標航跡之間一般為不等長航跡序列,即ni≠njξ。
顯然,在進行目標航跡關聯時,由于雷達1航跡集合中至多有一條航跡與雷達2航跡集合中的一條航跡成功關聯,可記雷達1航跡i與雷達2航跡ξj源于同一目標為事件Hij;雷達1航跡i與雷達2航跡ξk源于同一目標為事件Hik。則若航跡i與ξj確實來自同一個目標并成功被關聯,應滿足以下準則:
p(Hij)gt;p(Hik)(5)
式中:k≠j,k=1,2,…,n;p(·)表征為根據某一關聯準則計算出的事件發生可能的大小。
由此,航跡關聯問題可轉換為尋找合適關聯準則下的事件判決問題,或者也可同現有航跡關聯算法一樣,等效于構造某個指標表征目標航跡之間的相似度,如目標航跡之間的灰色區間相對支持度[18]和區域覆蓋度[19]。但在大多數情況下,由于存在航跡誤關聯情況,所以一般會先獲得航跡關聯矩陣或航跡關聯代價矩陣,再利用經典分配等算法,進行全局最優或代價最小的目標航跡關聯判決[27]。
2 目標量測誤差空間的概率分布
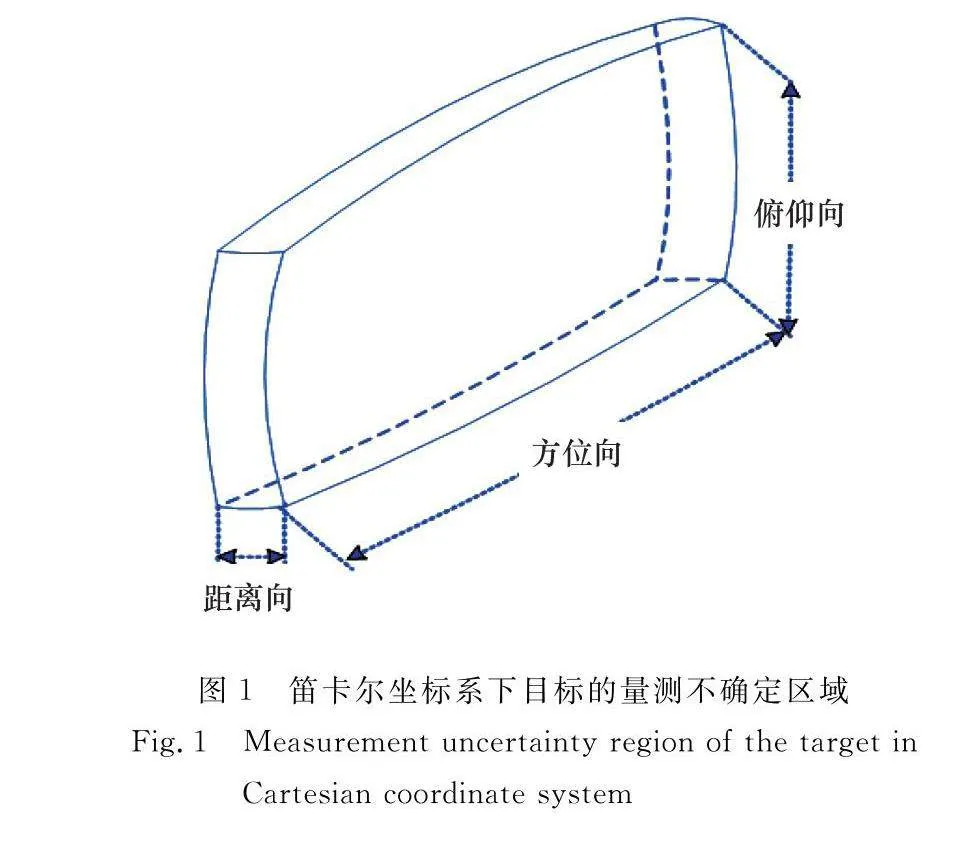
目標空間位置信息的獲取是雷達最基本的任務,其不外乎目標徑向距離r、方位角a和俯仰角e等目標參數的探測、濾波和估計。由于雷達設備工作機制、使用信號波形參數的不同,可獲取目標參量的維度、個數、目標量測誤差的空間概率分布特征和范圍也會有所差別[28-29]。
這里關注跟蹤測量雷達對目標量測誤差空間的概率分布特征,假設目標徑向距離、方位角和俯仰角信息已知。
顯然,由熱噪聲引起的角度和距離誤差一般認為都服從高斯隨機分布,角度和距離誤差均方根表示如下:
σθ=θ0.5k2SNR(6)
σR=cτe22n·SNR(7)
式中:θ0.5為雷達半波束寬度;SNR為雷達信號匹配輸出的信噪比;k為常數;c為光速;τe是脈壓后的脈寬;n為平滑脈沖個數。
而其他因目標閃爍、數據量化和脈沖抖動等因素引起的角度和距離誤差成分各自共同疊加在一起,均可認為距離向和角度向的誤差分布近似為非零的高斯噪聲分布。
但不同的是,僅從數值上看,角度誤差不隨目標距離變化。但若在笛卡爾空間觀察,隨目標探測距離變遠,目標在方位向和俯仰向的空間不確定范圍將逐步增大,遠大于有限的距離誤差,目標的空間定位誤差變大。
最終,目標的誤差空間分布為典型的“西瓜皮”形狀,如圖1所示。
3 基于目標量測誤差分布的航跡抗差
關聯算法3.1 基本思想
為便于描述將當前時刻探測的兩條目標航跡的航跡點關聯為同一目標程度的大小,有如下定義。
定義視同因子。對目標進行同一性識別時,用以表征將目標觀測值視為來源于對同一個目標觀測的可能性大小,取值范圍為0~1。視同因子越大,關聯為同一目標的可能性越大。
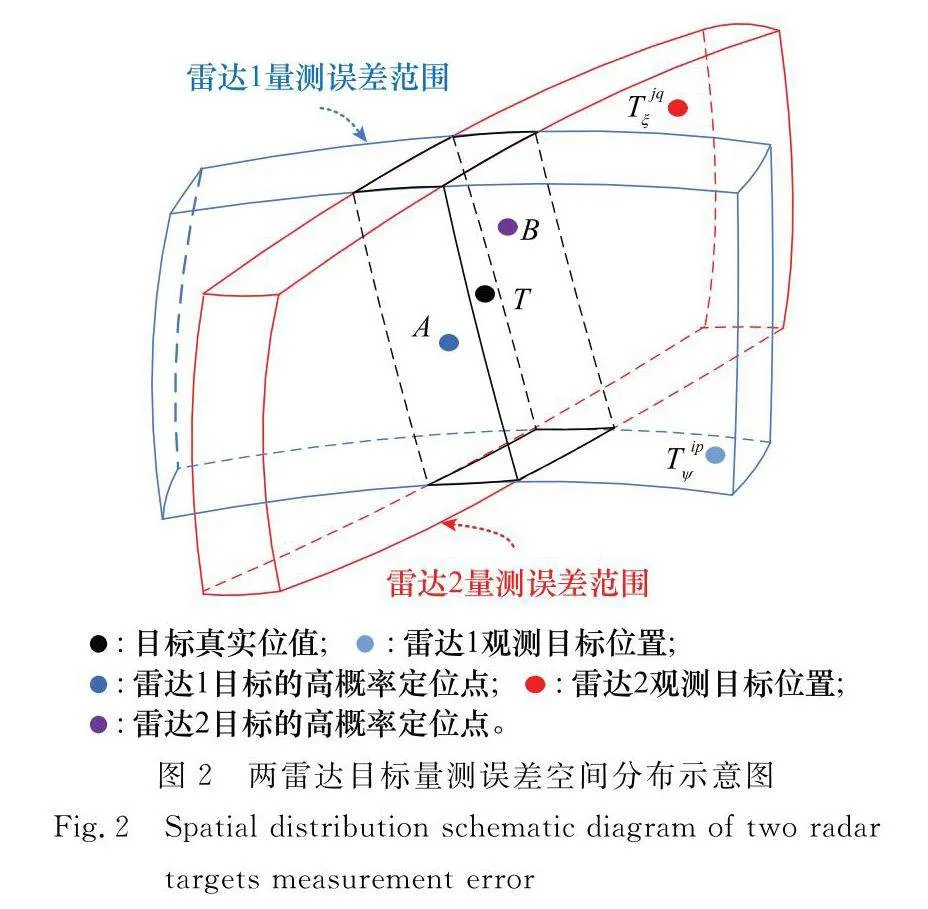
以兩雷達目標航跡關聯為例,兩雷達在對空間中同一遠距離目標進行觀測時,其目標量測誤差空間分布的不確定區域如圖2所示。
其中,目標量測值是雷達在測量誤差條件下對目標真實位置觀測的先驗概率值;高概率定位點則是指基于另一雷達對目標的量測值、誤差分布特征、雷達和目標的空間拓撲結構關系等各種先驗信息對目標進行二次定位后得到的后驗概率估計值;雷達1和雷達2對目標的量測誤差范圍(藍色“西瓜皮”區域和紅色“西瓜皮”區域),則是為囊括目標誤差空間分布范圍,且因距離和角度維誤差分布為高斯分布,對其距離向和角度向的最大單側誤差分布范圍均取1倍系統誤差與4倍起伏誤差均方根之和組成。
顯然,如果選用測距精度較高的雷達,兩雷達目標量測誤差空間存在明顯的互補特性,其相交區域為目標探測存在的高概率空間(黑色區域),可在其中計算得到兩雷達各自對目標的高概率定位點(不唯一)。同時可以發現,利用同源目標的先驗信息,計算兩雷達各自目標的高概率定位點與其雷達觀測值的誤差大小,均在其誤差空間分布范圍內。
所以,基于上述特點,可對目標航跡進行關聯。雖然兩雷達對目標的高概率定位點A和B均未知,但仍可利用另一雷達對目標測量的距離信息,基于兩雷達和觀測目標之間的幾何關系,近似計算兩雷達目標量測值Tip和Tjqξ距離的高概率定位點在方位向上的橫向距離偏差,并將其轉換成方位向上的角度偏差,最后利用該角度偏差計算得到視同因子。
若兩目標量測值同源,則計算得到的方位向的角度偏差最小,用于判斷其關聯為同一目標T的視同因子p(T|Tip)和p(T|Tjqξ)之積應最大。故可計算多幀下的視同因子之積,將其取平均后用以表征兩條目標航跡關聯程度的大小,再利用經典分配等算法進行全局最優航跡關聯。
3.2 目標關聯度函數
判斷兩雷達目標量測值是否同源,需要計算視同因子,其計算函數為目標關聯度函數。函數值表征的是兩目標關聯為同一個目標的可能性大小,也可以說是一個目標隸屬于另一個目標的程度大小。基于此,可利用模糊理論中的隸屬度函數計算視同因子的大小,隸屬度函數取值范圍為0~1,也正與視同因子的取值范圍一致。
由第3.1節可知,同源目標關聯時,方位向上計算的角度偏差越小,視同因子越大,所以隸屬度函數的選取應確保角度偏差越小(甚至為零)時,隸屬度函數取值越大并趨于1;反之,角度偏差越大,隸屬度函數的取值應越小并趨于0。此外,隸屬度函數曲線應具備較好的連續性、平滑性和可調節性,以適應雷達在不同測量誤差和系統誤差條件下觀測的目標航跡數據。
綜上所述,可選用高斯隸屬度函數作為目標關聯度函數,計算視同因子的大小。
高斯隸屬度函數,又稱為正態分布隸屬度函數,函數表達式為
式中:f(x)為參數x的隸屬度;μ為分布期望,即高斯函數的中心;σ為高斯函數的寬度。
高斯隸屬度函數圖像是一條位于x軸正上方的鐘形曲線,中心點處的隸屬度最高,隨著距離中心點的距離增加,隸屬度逐漸減小。
需要注意的是,當用高斯隸屬度函數計算視同因子時,μ=0,x為方位向上計算的角度偏差,而盡可能地囊括雷達在方位向上觀測所有目標的單側誤差范圍,σ可取雷達在方位向上的系統誤差與4倍隨機起伏誤差均方根之和。
所以,目標關聯度函數表達式為
3.3 算法步驟
3.3.1 時空統一
在實際工程中,雷達數據融合中心收到的各雷達上傳的目標航跡均是異步航跡,在進行目標航跡關聯前,需要完成各雷達數據間的空間統一和時間配準。
空間統一,主要指坐標統一,這里指不同觀測坐標系之間的互相轉換關系。考慮地球曲率和雷達布站等影響,且為符合工程實際應用,選擇雷達數據融合中心坐標系為大地坐標系,將兩雷達觀測目標數據轉換到雷達數據融合中心下。
時間配準的一般做法則是將各傳感器數據統一到掃描周期較長的一個傳感器上。目前,常用的方法有兩種:Blair等[30]提出的最小二乘配準法[30]和王寶樹等[31]提出的內插外推法。此外,也可利用濾波器得到的目標速度,將目標位置外推至需要的時刻,完成航跡同步。
雷達i在l時刻觀測目標T的北天東坐標為(XTi(l),YTi(l),ZTi(l)),i=1,2,而需要對準的時刻為l+Δt。若目標速度為(Vx,Vy,Vz),則外推公式如下所示:
3.3.2 視同因子的計算
在對兩雷達目標航跡完成時空統一后,在每一個時刻下,可依次計算用于判斷任意兩條目標航跡之間的航跡點是否關聯為同一目標的視同因子。
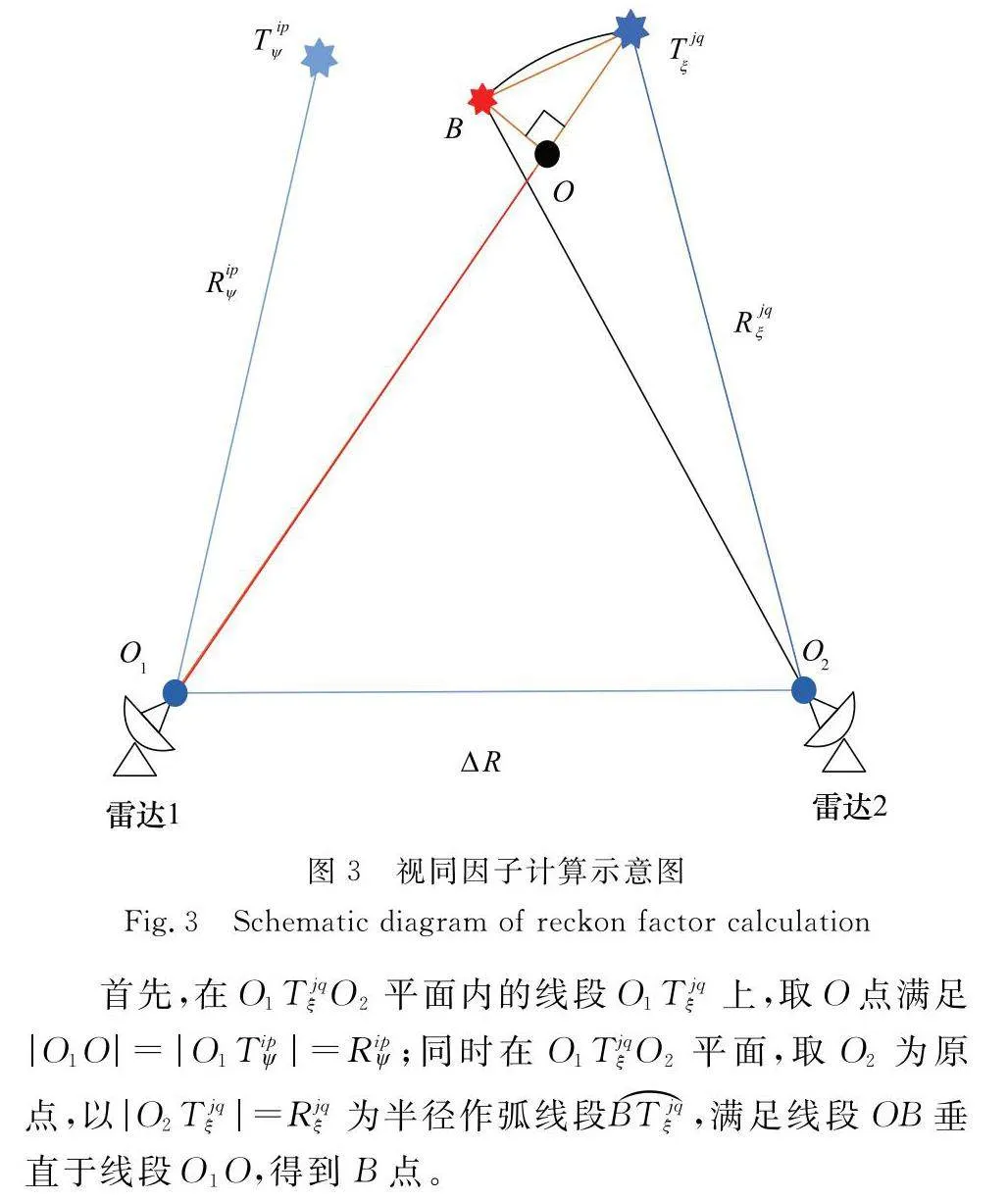
圖3為視同因子計算示意圖,本文在北天東直角坐標系下對兩雷達和目標進行分析。
首先,在O1TjqξO2平面內的線段O1Tjqξ上,取O點滿足|O1O|=|O1Tip|=Rip;同時在O1TjqξO2平面,取O2為原點,以|O2Tjqξ|=Rjqξ為半徑作弧線段BTjqξ,滿足線段OB垂直于線段O1O,得到B點。
然后,視同因子可按如下步驟進行計算。
步驟 1 計算Tjqξ到雷達1的距離|O1Tjqξ|。
步驟 2 計算雷達1到目標Tip和Tjqξ的距離誤差|OTjqξ|:
|OTjqξ|=||O1O|-|O1Tjqξ||(11)
雖然雷達1到目標Tjqξ的距離|O1Tjqξ|隱含了雷達2角度測量誤差帶來的影響,但若目標Tip和Tjqξ為同一目標,其徑向距離偏差|OTjqξ|的數值不會太大,故可設置一較大距離誤差門限η,對關聯目標進行粗篩選。
若滿足距離誤差門限,繼續步驟3;反之,兩雷達目標觀測值關聯為同一目標T的視同因子p(T|Tjqξ)值為零。
步驟 3 計算兩雷達與目標Tjqξ的視線夾角∠O1TjqξO2=θip_jq,表達式為
步驟 4 連接線段BTjqξ,假設兩雷達目標觀測值屬于同一目標T,基于兩雷達目標量測距離信息,可暫把B點(不唯一)當做Tjqξ的高概率定位點。
顯然,若兩雷達目標觀測值屬于同一目標,其方位向上的角度誤差∠BO2Tjqξ應小于雷達2在方位向上觀測目標的最大單側角度誤差分布范圍(最多為2°~3°)內,且由于目標距離較遠,弧線段BTjqξ和直線段BTjqξ長度可近似相等,可用|BTjqξ|表征目標量測值Tjqξ與其高概率定位點B在方位向上的橫向距離偏差。
進一步地,在遠距離情況下,在雷達目標視線切線方向上,基于幾何近似,∠BTjqξO2可近似為90°,則有∠OBTjqξ≈θip_jq。
故跨雷達計算的目標距離誤差|OTjqξ|可轉換為在雷達2方位向上帶來的橫向距離偏差|BTjqξ|,從而可將|OTjqξ|轉換為角度偏差uip_jq:
uip_jq=|BTjqξ|Rjqξ=|OTjqξ|sin(θip_jq)Rjqξ(13)
步驟 5 計算視同因子p(T|Tjqξ):
式中:ωA2為雷達2在方位向上的最大單側角度誤差范圍,ωA2=ΔA2+4σA2,ΔA2是雷達2在方位向上的系統誤差,σA2是雷達2在方位向上的隨機誤差均方根值。
步驟 6 交換目標Tjqξ和Tip,基于以上步驟,同理可得p(T|Tip)。
步驟 7 實際上,若兩雷達目標觀測值Tjqξ和Tip屬于不同目標,計算出的p(T|Tip)和p(T|Tjqξ)值偏差較大或兩者都很小,故可取一較大的視同因子偏差門限φ進行判別,0lt;φlt;1。
若p(T|Tip)和p(T|Tjqξ)兩者數值偏差大于φ,則用于判斷兩目標航跡之間的航跡點最終是否關聯為同一目標的視同因子p(T|Tip,Tjqξ)的值為0;反之,可取兩視同因子p(T|Tip)和p(T|Tjqξ)的乘積表征p(T|Tip,Tjqξ):
p(T|Tip,Tjqξ)=p(T|Tip)p(T|Tjqξ)(15)
3.3.3 航跡關聯度
航跡關聯度主要用于判斷兩條或多條目標航跡是否關聯為同一目標。
在對目標航跡進行時空統一后,兩雷達間任意目標航跡i和ξj可組成一對航跡序列等長的航跡關聯對(i,ξj),可令ni=njξ=N。
而對于目標航跡i和ξj的航跡關聯度?ij,0≤?ij≤1,可用關于兩條目標航跡之間每一幀的航跡點對(Tip,Tjqξ),計算視同因子p(T|Tip,Tjqξ)并對其取平均后的值表征:
?ij=1N∑Np=q=1p(T|Tip,Tjqξ)(16)
3.3.4 航跡關聯判決
當求得目標航跡關聯度?ij后,可將目標航跡關聯錯誤代價定義為γij=1-?ij,得m×n維的目標航跡關聯代價矩陣Φm×n=[γij]。
令變量:
χij=1, 表示航跡i和航跡j對應同一個目標
0, 表示航跡i和航跡j對應不同目標
目標函數記為
L=∑mi=1∑nj=1χijγij(17)
則可構成以下二維分配[27]問題:
對于該二維分配問題,可將其等價為一個帶權二分圖的最優匹配問題,γij即為二分圖的兩個節點i和j之間的權值,可采用KM(Kuhn-Munkres)算法進行求解。
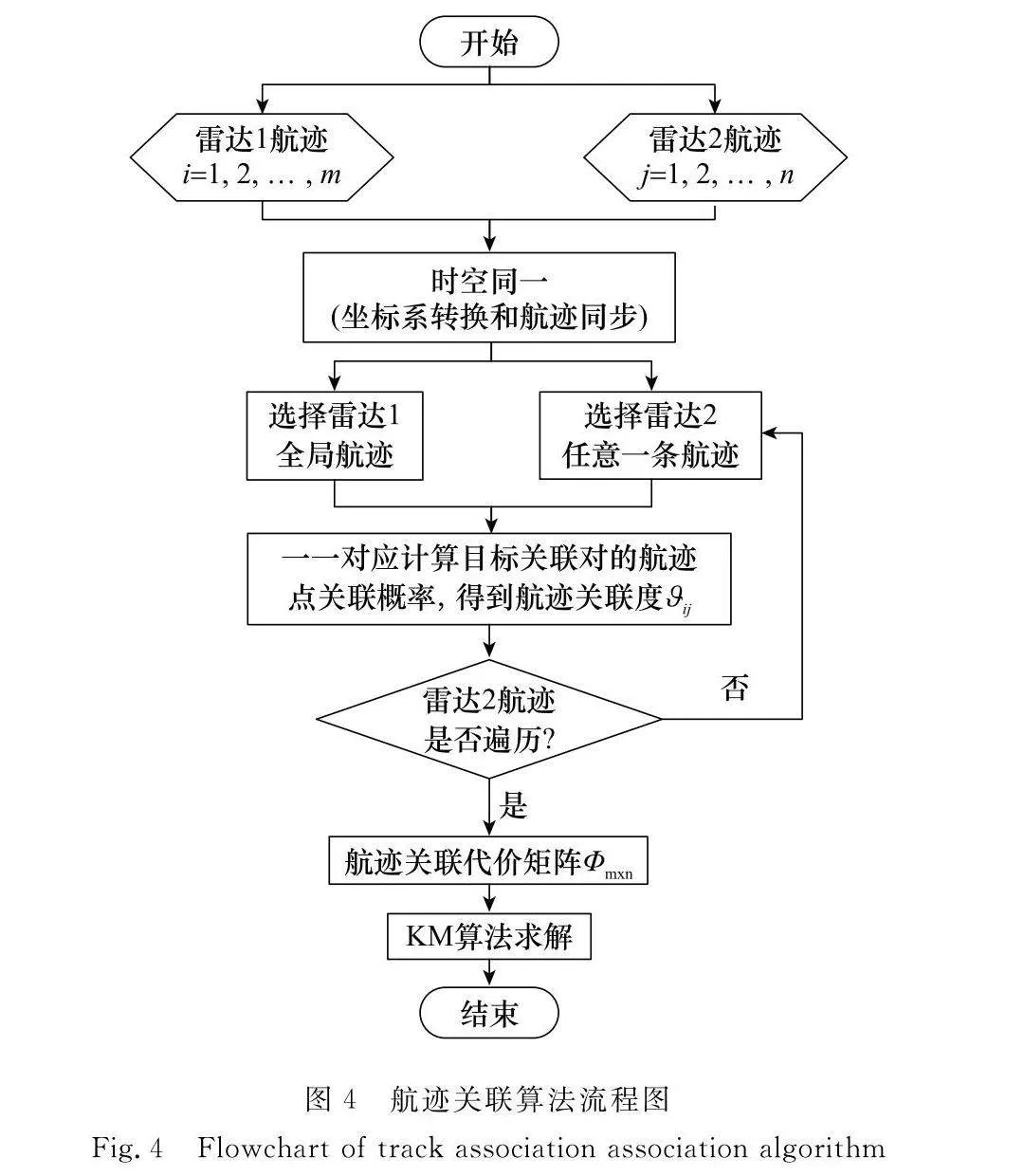
3.4 算法流程
綜上所述,基于目標量測誤差分布的航跡抗差關聯算法流程圖如圖4所示。
4 仿真驗證分析
為驗證本文所提航跡抗差關聯算法的性能,且在因角度維誤差而導致遠距離目標空間定位誤差變大的情況下,能很好地解決密集目標航跡誤關聯率高的問題,將本文所提航跡抗差關聯算法同文獻[20]和文獻[27]所提現有航跡關聯算法性能較好的算法進行對比。
通過設置不同參數下的場景進行仿真,采用正確關聯概率Ec和錯誤關聯概率Ee作為航跡關聯結果的評價指標,給出各算法之間的仿真結果和對比分析。
4.1 仿真環境
為突顯本文所提算法的優越性,考慮兩雷達均有較大的測距和測角隨機誤差,這里假設某分布式系統中有兩部異地配置且相距40 km的單基地雷達,雷達1采樣周期為0.4 s,雷達2采樣周期為0.6 s。兩雷達的最大測距系統誤差為100 m,測角系統誤差為0.5°,測距隨機誤差均方根為200 m,測角隨機誤差均方根則為2°。
兩雷達對300 km外同一空域內的200批目標進行跟蹤,并假設所有目標在空間中的不同高度下等高勻速平飛,目標起始運動方向隨機分布在0~2π rad內,而初速度大小則隨機分布在200~400 m/s內。兩雷達對目標持續跟蹤20 s后,將目標航跡數據上傳至融合中心,共進行100次蒙特卡羅仿真實驗。
其中在對目標航跡進行關聯時,由于目標在遠距離情況下因角度誤差導致目標空間定位精度變差,跨雷達計算同一目標量測距離的誤差值也會較大。故距離誤差門限η的取值可通過預估目標的最大測角誤差,基于兩雷達對目標的量測距離和視線夾角,依據式(13)取一預估值。而在本文所設目標仿真場景下,η可取5~9 km。在100次的蒙特卡羅仿真實驗中,η取值為7 km,視同因子偏差門限φ則可取較大值,一般取0.5即可。
4.2 算法關聯效果對比
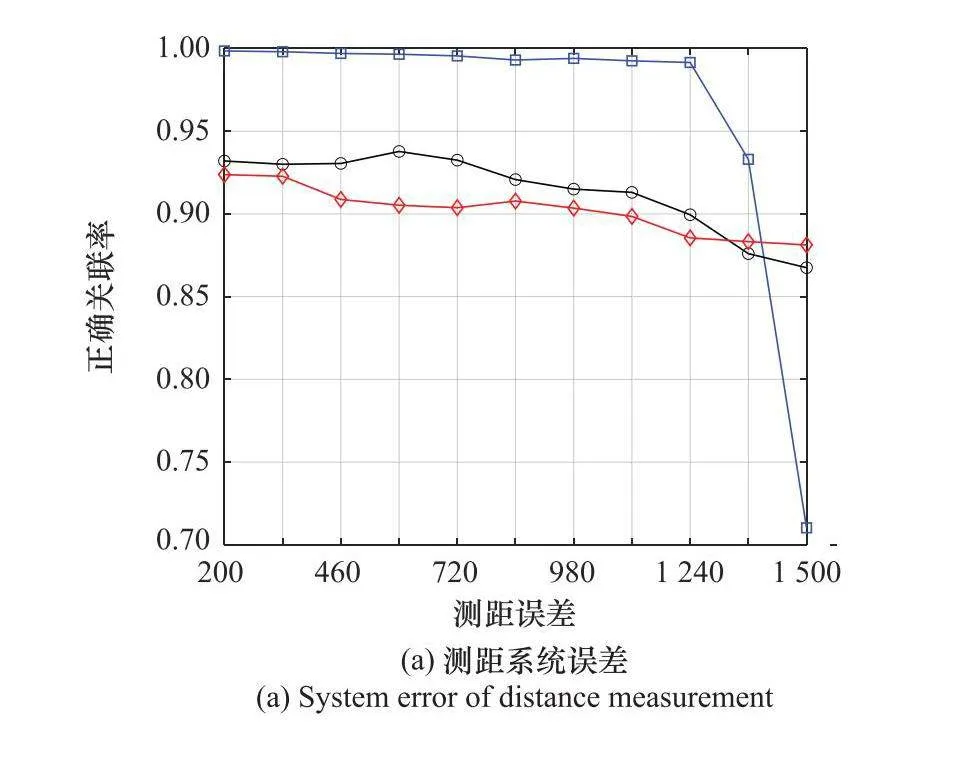
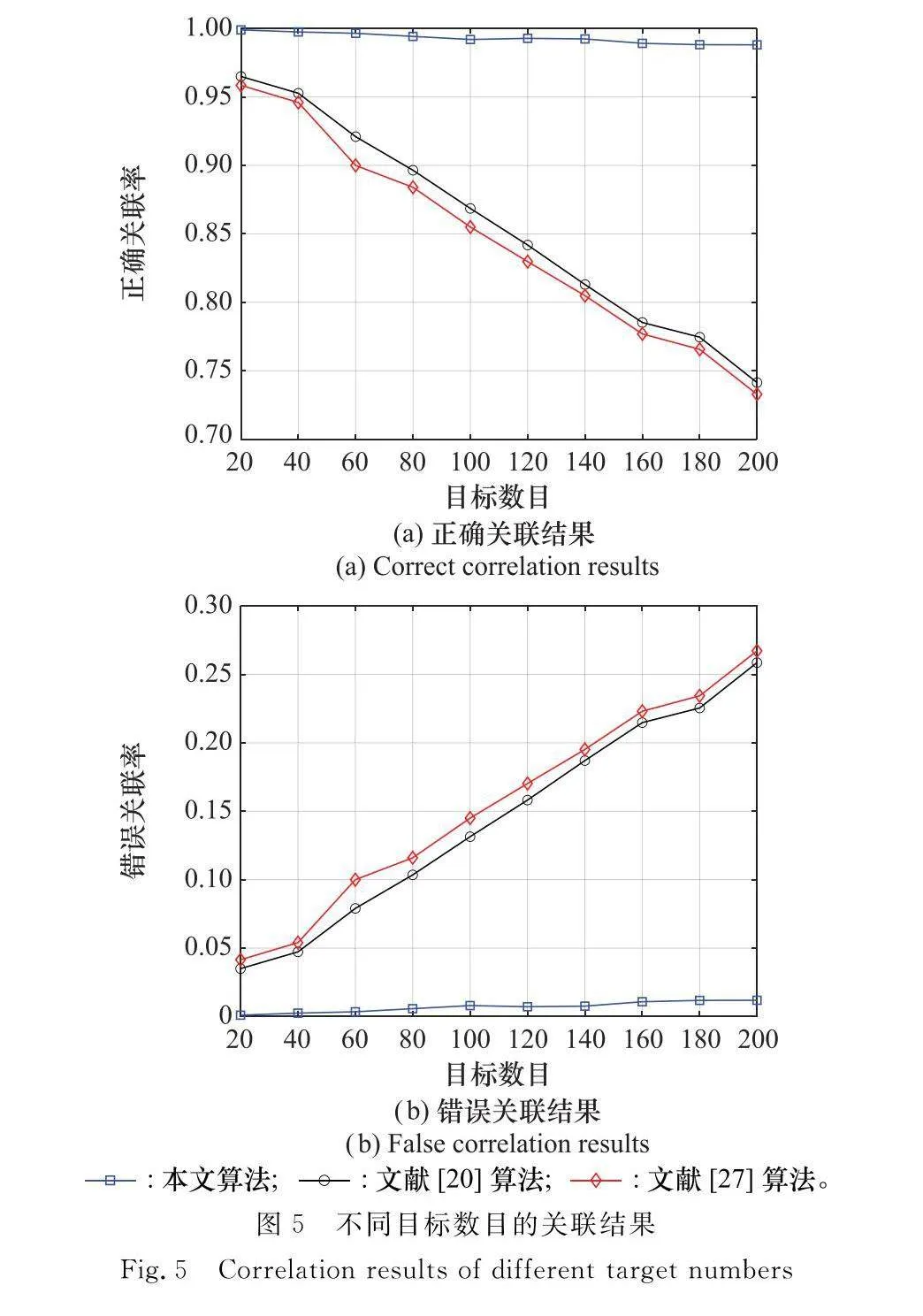
首先,改變仿真環境中的目標數目,其他參數保持不變,目標密集程度對算法正確關聯率和錯誤關聯率的影響如圖5所示。
從圖5可以看出,當目標數目增多時,文獻[20]和文獻[27]算法的正確關聯率下降較明顯,目標航跡錯誤關聯率均逐步增大至25%左右。而本文算法不受目標密集程度的影響,其正確關聯率均較高且都在98.5%以上,錯誤關聯率在1.5%以下。這是由于文獻[20]的序貫修正灰關聯法和文獻[27]的k近鄰平均距離法均利用了目標航跡點在空間中的歐式距離信息,算法關聯效果與目標的空間定位精度的大小有關。
當目標距離越遠時,尤其目標密集分布且位于300 km外的遠距離情況下,測角誤差會導致目標在空間中的定位精度變得極差,特別是當測角隨機誤差較大時,這一現象更加明顯,所以文獻[20]和文獻[27]算法的關聯準確率越來越低,錯誤關聯率越來越高。此外,相對文獻[27]算法而言,文獻[20]的算法雖然需要對異步航跡進行同步,但由于在航跡關聯時,考慮了目標歷史時間序列的航跡信息,對灰關聯度進行了修正,所以算法效果相對較好。
相比測角誤差導致遠距離目標在角度維存在較大的空間定位誤差的情況,本文算法利用了遠距離目標的距離向誤差有限這一特征,引入目標量測距離信息,充分利用目標與兩雷達的空間關系和雷達站址等先驗信息,計算視同因子和目標航跡關聯度,進行全局最優航跡關聯,大大降低了測角誤差給航跡關聯帶來的影響,算法正確關聯率高,效果最好。
4.3 抗差關聯性能比較
為檢驗兩雷達在不同測距與測角系統誤差和隨機誤差情況下,本文所提算法的抗差關聯性能,這里將兩雷達測角隨機誤差均方根值設為1°,仿真環境中的其他參數不變。然后,進行100次蒙特卡羅仿真實驗,得到文獻[20]和文獻[27]算法對200批目標航跡的正確關聯概率分別為94.95%和95.78%,本文算法的正確關聯率則為99.81%,再次證明了本文算法關聯性能最好。最后,分別改變雷達2的測距與測角系統誤差和隨機誤差均方根,觀察不同誤差條件對兩雷達算法正確關聯率的影響。
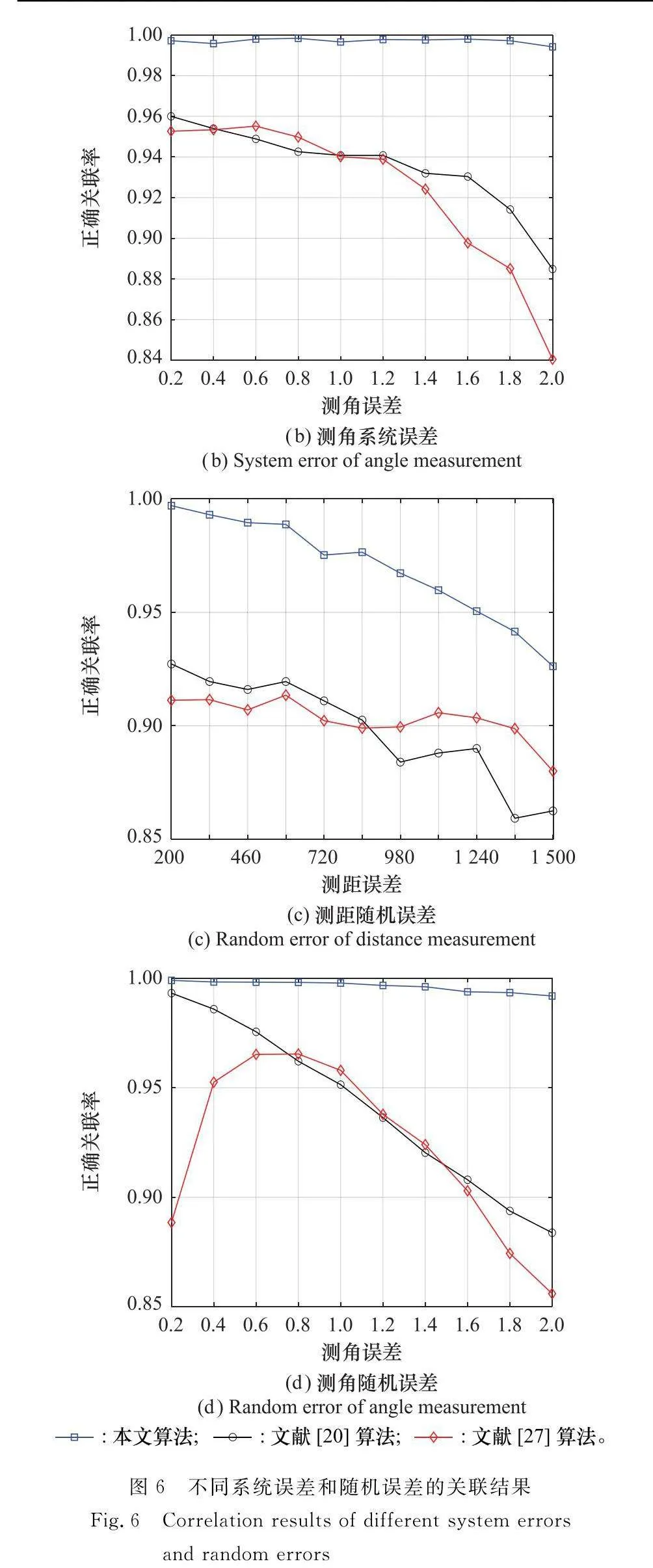
圖6(a)和圖6(b)分別給出了3種算法在不同測距和測角系統誤差情況下的關聯結果。圖6(c)和圖6(d)則分別給出了3種算法在不同測距和測角隨機誤差均方根情況下的關聯結果。
如圖6(b)和圖6(d)所示,對測角系統誤差和隨機誤差均方根變化來說,當測角系統誤差和隨機誤差均方根逐漸增大時,文獻[20]算法的正確關聯率也同圖6(a)和圖6(c)一樣呈明顯下降趨勢,且因角度維誤差引起的目標空間定位誤差較大,目標的航跡正確關聯率變化較大,整體分別下降了7.51%和10.94%。
同理,測角系統誤差和隨機誤差均方根變化對文獻[27]的航跡關聯算法影響也較大。不同的是,當雷達2測角系統誤差和測角隨機誤差均方根分別在0.6°和0.8°向左右兩側擴散時,前者算法的正確關聯率在左右兩側分別下降025%和11.22%,后者則分別下降了7.69%和10.12%。
這是由于文獻[27]算法關聯的前提是應使用觀測目標精度差距不大的兩雷達,因為一旦兩個雷達觀測同一空間目標的精度差距較大,在對密集目標進行航跡關聯時,航跡間的k近鄰平均距離增大,目標正確關聯的可靠性降低,導致航跡誤關聯率增大。如圖6(b)和圖6(d)所示,雷達1測角系統誤差和測角隨機誤差均方根分別為0.5°和1°,加之受雷達布站影響,當雷達2測角系統誤差和測角隨機誤差均方根分別在0.6°和0.8°向左右兩側擴散時,兩雷達觀測同一空間目標的精度差距增大,航跡間的k近鄰平均距離增大致使在進行全局最優航跡關聯時,航跡誤關聯率升高,文獻[27]算法的航跡正確關聯率才在其左右兩側存在下降趨勢。
由于本文算法核心是不依賴于目標測角信息,而是基于兩雷達對遠距離目標的量測距離誤差有限這一特征,將跨雷達計算的目標距離誤差轉換為其方位向的角度偏差,基于角度偏差信息進行視同因子計算和后續目標航跡關聯,雷達測角誤差的變化對算法關聯性能影響不大。
而針對本文所設仿真場景,在圖6(c)中,當雷達2測距隨機誤差增大時,本文算法正確關聯率雖然明顯下降,但關聯性能是最優的。這主要是由于在計算目標視同因子和航跡關聯度時,目標運動特性和分散區域不同,本文算法關注了目標歷史航跡信息,且在計算多幀視同因子并取平均來表征目標航跡關聯度后,進行全局最優航跡關聯判決,最大可能地降低了測距隨機誤差對目標航跡正確關聯的影響。此外,由于目標測距誤差增大,目標在空間中的定位誤差也增大,故文獻[20]和文獻[27]算法的目標航跡正確關聯率同圖6(a)中一樣,出現下降趨勢。
對于距離向來說,同樣在圖6(a)中,在本文所設仿真場景下,雷達1測距系統誤差為100 m,當雷達2測距系統誤差增大時,若兩雷達測距系統的誤差不超過1 200 m,相比文獻[20]和文獻[27]所提算法,本文算法仍具有較高的正確關聯率;反之,算法正確關聯率會迅速下降。這是由于本文所提算法隱含了跨雷達計算同一目標的距離偏差|OTjqξ|最小這一假設,當兩雷達的測距精度差距比較大時,尤其是當其中某一雷達存在較大距離系統誤差時,在三維空間中跨雷達計算的同一目標的距離偏差|OTjqξ|會變大。由式(13)和式(14)可知,這雖然會影響視同因子的計算,降低關聯正確率,但是只要兩雷達對目標測距精度的差距不超過某個范圍,加之考慮了目標歷史航跡信息、目標運動特性和分散區域的不同,本文所提算法的假設仍然成立,且通過進行全局最優航跡關聯判決,在一定程度上盡可能保證了算法的有效性,正確關聯率下降不明顯;反之,本文算法關聯性能則會迅速下降。這也進一步表明了本文所提目標航跡關聯算法適用于在雷達之間測距精度較高且測距誤差不是很大的情況下進行目標航跡關聯。
需要說明的是,前文所述兩雷達對目標測距精度的差距范圍的大小,與雷達和目標之間的相對位置關系、目標密集程度和目標運動特性有關。但在實際工程中,無論是系統誤差還是隨機起伏誤差,雷達對目標的測距和測角誤差不可能很大,且雷達之間的測量精度也基本差距不大。本文所述仿真場景只用于進行綜合仿真論證,凸顯本文所提算法的優越性,也進一步表明了本文算法的適用性較高。
綜上所述,在實際工程中,在不同測距與測角的系統誤差和隨機誤差情況下,本文所提算法的航跡誤關聯率最高,抗差關聯性能最好。
5 結 論
本文提出了一種基于目標量測誤差分布的航跡抗差關聯算法,算法主要利用雷達目標量測距離信息,基于測距誤差有限這一特征,充分考慮了兩雷達站址、目標量測誤差分布特征和雷達與目標的空間幾何關系,計算得到用于判斷目標航跡點是否關聯的視同因子與航跡關聯度,最后利用經典分配法進行航跡關聯判決。
仿真結果表明,本文所述算法在距離遠、目標密集、系統誤差與隨機起伏誤差較大場景下,航跡正確關聯率高、抗差性好,克服了現有航跡關聯算法由測角誤差導致遠距離目標空間定位誤差較大而存在航跡誤關聯率高的不足。
參考文獻
[1]CHAI L, YI W, KONG L J. Joint sensor registration and multi-object tracking with PHD filter in distributed multi-sensor networks[J]. Signal Processing, 2023, 206: 108909.
[2]曾雅俊, 王俊, 魏少明, 等. 分布式多傳感器多目標跟蹤方法綜述[J]. 雷達學報, 2023, 12(1): 197-213.
ZENG Y J, WANG J, WEI S M, et al. Review of the method for distributed multi-sensor multi-target tracking[J]. Journal of Radars, 2023, 12(1): 197-213.
[3]ZHU H, WANG M L, YUEN K V, et al. Track-to-track association by coherent point drift[J]. IEEE Signal Processing Letters, 2017, 24(5): 643-647.
[4]ZOU K, ZHU H, LI Y F, et al. Track-to-track association for intelligent vehicles by preserving local track geometry[J]. Sensors, 2020, 20(5): 1412.
[5]LI B Z, DONG Y L, HUANG G D, et al. Radar/ESM anti-bias track association algorithm based on track distance vector detection[J]. The Journal of Engineering, 2019, 2019(21): 7563-7567.
[6]CUI Y Q, LIU Y, TANG T T, et al. A new adaptive track correlation method for multiple scenarios[J]. IET Radar, Sonar Navigation, 2021, 15(9): 1112-1124.
[7]賴文星, 王創維, 顧樹峰, 等. 一體化防空協同組網作戰研究[J]. 空天防御, 2022, 5(4): 92-96.
LAI W X, WANG C W, GU S F, et al. Integrated air defense cooperative networking operation research[J]. Air and Space Defense, 2022, 5(4): 92-96.
[8]雒梅逸香. 基于組網雷達數據融合的目標跟蹤技術研究[D]. 西安: 西安電子科技大學, 2018.
LUOMEI Y X. Study on target tracking technology based on radar network data fusion[D]. Xi’an: Xidian University, 2018.
[9]郭凱德. 組網雷達協同探測技術研究[D]. 西安: 西安電子科技大學, 2019.
GUO K D. Research on cooperative detection technology of networked radar[D]. Xi’an: Xidian University, 2019.
[10]LIU Y, HE Y, DONG K, et al. Fuzzy binary track correlation algorithms for multisensor information fusion[J]. Journal of Networks, 2014,9(3): 672-681.
[11]TOKTA A, HOCAOGLU A K. Sensor bias estimation for track-to-track association[J]. IEEE Signal Processing. Letters, 2019, 26(10): 1426-1430.
[12]ZHU H Y,WANG C. Joint track to track association and sensor registration at the track level[J]. Digital Signal Processing, 2015, 41: 48-59.
[13]魏兵桌, 劉鑫, 曹政, 等. 一種基于統計的二維航跡關聯方法[J]. 空天防御, 2020, 3(1): 93-98.
WEI B Z, LIU X, CAO Z, et al. A two-dimensional track correlation method based on statistics[J]. Air and Space Defense, 2020, 3(1): 93-98.
[14]何友, 宋強, 熊偉. 基于傅里葉變換的航跡對準關聯算法[J]. 航空學報, 2010, 31(2): 356-362.
HE Y, SONG Q, XIONG W. A track registration correlation algorithm based on Fourier transform[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(2): 356-362.
[15]何友, 宋強, 熊偉. 基于相位相關的航跡對準關聯技術[J]. 電子學報, 2010, 38(12): 2718-2723.
HE Y, SONG Q, XIONG W. Track alignment-correlation technique based on phase correlation[J]. Acta Electronica Sinica, 2010, 38(12): 2718-2723.
[16]MOUSA N, SAEID P, LEILI M K. An adaptive density-based fuzzy clustering track association for distributed tracking system[J]. IEEE Access, 2019, 7: 135972-135981.
[17]衣曉, 張懷巍, 曹昕瑩, 等. 基于區間灰數的分布式多目標航跡關聯算法[J]. 航空學報, 2013, 34(2): 352-360.
YI X, ZHANG H W, CAO X Y, et al. A track association algorithm for distributed multi-target systems based on gray interval numbers[J]. Acta Aeronautica et AstronauticaSinica, 2013, 34(2): 352-360.
[18]楊軍佳, 張培峰, 納學柱. 雷達組網航跡灰色關聯方法[J]. 電訊技術, 2019, 59(3): 318-322.
YANG J J, ZHANG P F, NA X Z. A grey method of radar network track association[J]. Telecommunication Engineering, 2019, 59(3): 318-322.
[19]衣曉, 周威. 基于區域覆蓋度的航跡灰關聯算法[J]. 火力與指揮控制, 2020, 45(5): 45-50.
YI X, ZHOU W. Track grey correlation algorithm based on regional coverage[J]. Fire Control amp; Command Control, 2020, 45(5): 45-50.
[20]董凱, 關欣, 王海鵬, 等. 基于序貫修正灰關聯度的全局最優航跡關聯算法[J]. 電子與信息學報, 2014, 36(8): 1939-1945.
DONG K, GUAN X, WANG H P, et al. Global optimal track association algorithm based on sequential modified grey association degree[J]. Journal of Electronics amp; Information Technology, 2014, 36(8): 1939-1945.
[21]ZHU H Y, HAN S Y. Track-to-track association based on structural similarity in the presence of sensor biases[J]. Journal of Applied Mathematics, 2014(1): 294657.
[22]董凱, 王海鵬, 劉瑜. 基于拓撲統計距離的航跡抗差關聯算法[J]. 電子與信息學報, 2015, 37(1): 50-55.
DONG K, WANG H P, LIU Y. Anti-bias track association algorithm based on topology statistical distance[J]. Journal of Electronics amp; Information Technology, 2015, 37(1): 50-55.
[23]QI L, HE Y, DONG K, et al. Multi-radar anti-bias track association based on the reference topology feature[J]. IET Radar Sonar amp; Navigation, 2018, 12(3): 366-372.
[24]崔亞奇, 熊偉, 顧祥岐. 基于三角穩定的海上目標航跡抗差關聯算法[J]. 系統工程與電子技術, 2020, 42(10): 2223-2230.
CUI Y Q, XIONG W, GU X Q. Anti-bias association algorithm for marine target track based on triangular stability[J]. Systems Engineering and Electronics, 2020, 42(10): 2223-2230.
[25]齊林, 熊偉, 何友. 基于距離分級聚類的機載雷達航跡抗差關聯算法[J]. 電子學報, 2018, 46(6): 1475-1481.
QI L, XIONG W, HE Y. Anti-bias track-to-track association algorithm for aircraft platforms based on distance hierarchical clustering[J]. Acta Electronica Sinica, 2018, 46(6): 1475-1481.
[26]崔亞奇, 熊偉, 唐田田. 一種基于時空交叉點新特征的航跡關聯算法[J]. 電子與信息學報, 2020, 42(10): 2500-2507.
CUI Y Q, XIONG W, TANG T T. A track correlation algorithm based on new space-time cross-point feature[J]. Journal of Electronics amp; Information Technology, 2020, 42(10): 2500-2507.
[27]衣曉, 曾睿. 基于k近鄰平均距離的異步航跡關聯算法[J]. 系統工程與電子技術, 2022, 44(11): 3515-3521.
YI X, ZENG R. Asynchronous track-to-track association algorithm based on k means distance of nearest neighbors[J]. Systems Engineering and Electronics, 2022, 44(11): 3515-3521.
[28]于選桐, 劉唐興, 王號, 等. 組網雷達分布式誤差估計方法[J]. 信息化研究, 2020, 46(4): 21-24.
YU X T, LIU T X, WANG H, et al. Distribute error estimation method of netlike radar[J]. Information Research, 2020, 46(4): 21-24.
[29]李國君, 孔博. 空饋式雷達目標模擬誤差分析方法研究[J]. 艦船電子工程, 2023, 43(7): 74-78.
LI G J, KONG B. Research on analysis method of space radiation radar target simulation error[J]. Ship Electronic Engineering, 2023, 43(7): 74-78.
[30]BLAIR W D, RICE T R, ALOUANI A T, et al. Asynchronous data fusion for target tracking with a multitasking radar and optical sensor [C]∥Proc.of the SPIE Conference on Acquisition, Tracking and Pointing, 1991: 234-245.
[31]王寶樹, 李芳社. 基于數據融合技術的多目標跟蹤算法研究[J]. 西安電子科技大學學報, 1998, 25(3): 269-272.
WANG B S, LI F S. The research on multiple targets tracking based on data fusion technology[J]. Journal of Xidian University, 1998, 25(3): 269-272.
作者簡介
楊 鑫(1998—),男,碩士研究生,主要研究方向為航跡關聯、多傳感器數據融合。
阮開智(1985—),男,高級工程師,碩士,主要研究方向為武器系統設計。
劉紅明(1967—),男,高級工程師,博士,主要研究方向為信號處理、MIMO雷達。
王曉科(1984—),男,高級工程師,博士,主要研究方向武器系統設計。
劉靜秋(1991—),女,工程師,碩士,主要研究方向為軟件系統設計。
施裕升(1996—),男,助理工程師,碩士,主要研究方向為探測制導與系統設計。

