基于樣條插值的非線性自干擾對消技術

摘 要：

針對雷達干擾機收發天線之間存在的非線性自干擾耦合問題，研究一種基于樣條插值的非線性自干擾對消方法。該方法將樣條插值和自適應濾波相結合，分別建立樣條哈默斯坦模型和樣條維納模型，通過引入魯棒性較強的反正切（arctangent， ARC）函數作為代價函數，得到兩種模型下樣條控制點和濾波器系數的自適應學習規則，并分析樣條控制點數量對自干擾對消性能的影響。仿真實驗表明，對于帶寬為60 MHz的信號，所提基于ARC參數學習方法與傳統最小均方參數學習方法相比，對消比獲得4 dB左右的提升，收斂速度提高1倍。另外，針對信道突變的場景，所提方法跟蹤性能好且穩態誤差低。當背景噪聲中存在非高斯脈沖干擾時，所提方法能夠有效應對脈沖噪聲環境下的干擾。

關鍵詞：

非線性自干擾對消; 樣條插值; 反正切函數; 脈沖噪聲

中圖分類號：

TN 974

文獻標志碼： A""" DOI：10.12305/j.issn.1001-506X.2024.09.03

Nonlinear self-interference cancellation technique based on spline interpolation

ZHAO Zhongkai1，2，*， GUAN Zeyue1， LI Hu3

（1. College of Information and Communication Engineering， Harbin Engineering University， Harbin 150001， China;

2. Key Laboratory of Advanced Marine Communication and Information Technology， Ministry of Industry

and Information Technology， Harbin Engineering University， Harbin 150001， China;

3. Beijing Aerospace Long March Aircraft Research Institute， Beijing 100076， China）

Abstract：

In view of the nonlinear self-interference coupling problem between the transmitting and receiving antennas of radar jammer， a nonlinear self-interference cancellation method based on spline interpolation is studied. The method combines spline interpolation and adaptive filtering， and establishes the spline-based Hammerstein model and the spline-based Wiener model respectively. By introducing the robust arctangent （ARC） function as the cost function， the adaptive learning rules of the spline control points and filter coefficients under the two models are obtained， and the influence of the number of spline control points on the performance of the self-interference cancellation is analyzed. Simulation experiments show that for signals with a bandwidth of 60 MHz， the proposed ARC-based parameter learning method achieves about 4 dB improvement in the interference cancellation ratio compared with the traditional least mean square parameter learning methods， and the convergence speed can be improved by a factor of one. In addition， the method has good tracking performance and low steady-state error for the scenario of sudden channel change. When non-Gaussian pulse interference exists in the background noise， the proposed method can effectively cope with the interference in the impulse noise environment.

Keywords：

nonlinear self-interference cancellation; spline interpolation; arctangent （ARC） function; impulsive noise

0 引 言

電子戰在現代化戰爭中發揮著至關重要的作用，雷達干擾機作為重要的軍事武器，為保護藍方設備和干擾紅方雷達提供了保障。干擾機發射的干擾信號不僅對紅方產生了干擾，還會耦合至近端接收機形成自干擾，特別是對于機載、彈載等狹小的平臺，大功率的自干擾信號會影響接收機的正常工作、嚴重時甚至產生自激［1］。自干擾對消技術的核心要義在于根據參考信號，對自干擾信號進行準確的估計，并將估計的自干擾信號從接收信號中減去。目前，對消技術已被廣泛應用在5G同時同頻全雙工技術［2-3］、雷達直達波信號對消［4］、水聲帶內全雙工通信［5-6］等領域。按照抵消位置的不同，一般分為空域［7］、模擬域［8］和數字域對消［9-11］，由于數字域具備簡單、靈活的數字信號處理能力，因此探究高性能的數字對消技術是目前主流的研究方向［12］。高性能主要體現在：準確地還原自干擾、快速地適應信道的變化和計算復雜度低。傳統的自干擾對消將收發鏈路看成理想的線性系統，未考慮實際應用時引入的非線性因素，如功放非線性［13］、相位噪聲［14］、同相正交（in-phase/quadrature， I/Q）不平衡［15］等。目前研究表明，影響對消性能的主要限制因素是發射鏈路的功率放大器帶來的非線性失真［16］。盡管線性自干擾是能量占比大的部分，但如果不對非線性自干擾進行抵消，將會影響整個數字域的對消性能。

文獻［17］介紹一種基于箕舌線樣條插值的算法，該算法能夠準確估計出非線性系統的權值，但未給出復信號樣條插值算法的推導和分析。文獻［18］提出一種基于正則化的非線性自干擾對消方法，能夠提高系數估計精度并且避免參數過擬合，但隨著發射功率的增大，病態特性受噪聲的擾動減小，該方法的性能會受限。文獻［19］通過對線性對消殘差使用隨機傅里葉特征的最小均方（random Fourier features-least mean square， RFF-LMS）誤差算法，在保持性能相近的同時將計算復雜度降低了兩個數量級。文獻［20］提出一種基于二維正交化廣義線性復數最小均方（widely linear complex least mean square， WLCLMS）誤差的自干擾對消方法，通過特征值分解實現輸入信號的去相關，能夠在時變信道環境下完成實時跟蹤，但該方法的信號處理流程復雜并且正交化涉及大量矩陣運算，計算復雜度高。近年來隨著深度學習的不斷發展，學者們提出基于神經網絡的非線性對消方法［21］，通過將訓練樣本輸入神經網絡重建自干擾。但該方法需要一定的訓練時間和大量的數據，并且在迭代過程中容易陷入局部最優;另外，該網絡模型是針對固定信道場景下的，實際環境中信道特性是不斷動態變化的，因此存在實時性差的問題。無論是采用常規的最小二乘（least square， LS）算法還是深度學習的方法，在硬件實現時都對計算資源成本的要求較高，實現起來變得困難。

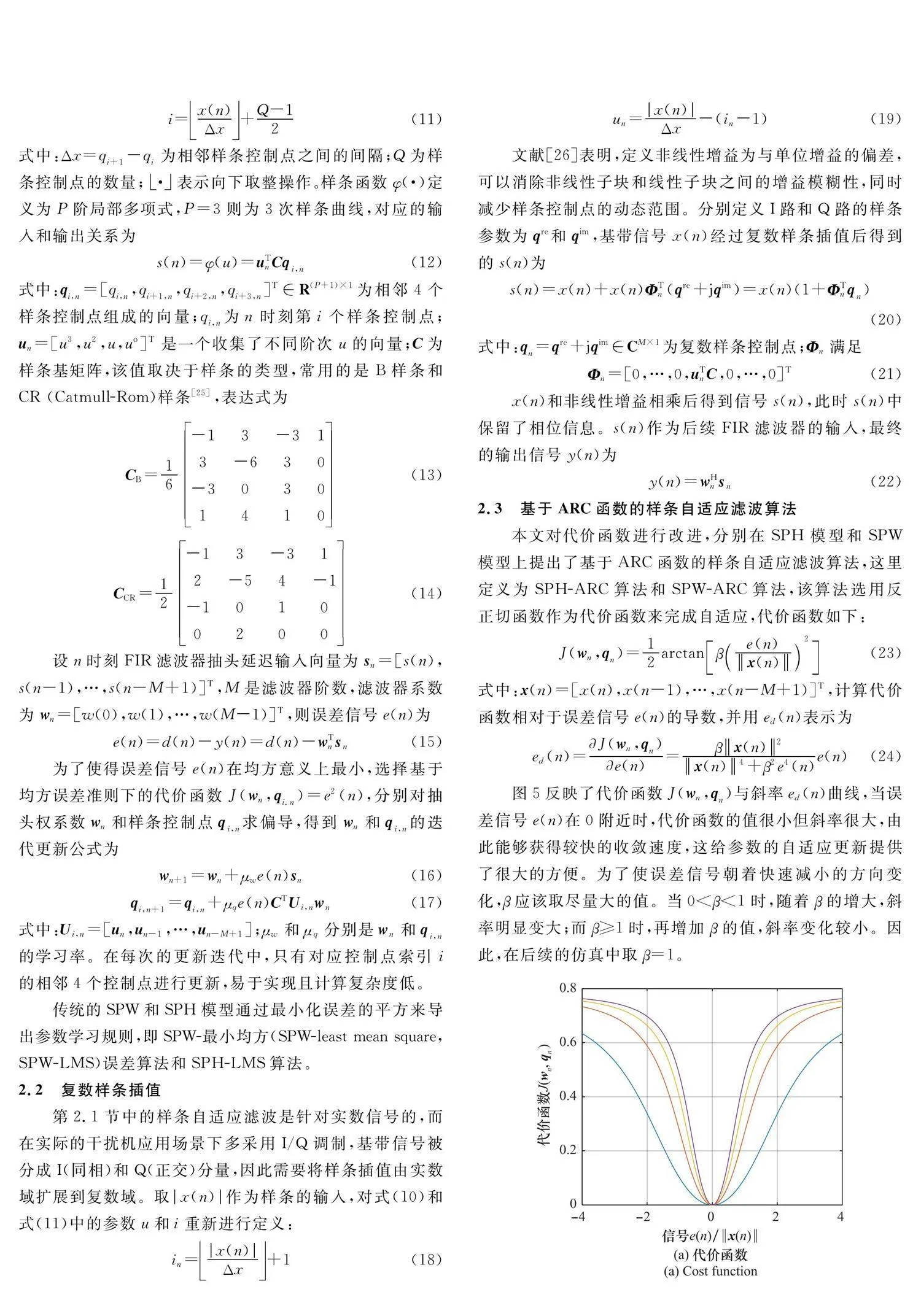
針對上述問題，本文研究了一種基于樣條插值的非線性自干擾對消方法。首先，分別建立樣條Hammerstein（spline-based Hammerstein， SPH）模型和樣條Wiener（spline-based Wiener， SPW）模型，并將樣條插值由實數域擴展到復數域。然后，基于反正切（arctangent， ARC）形式的代價函數，分別在兩種模型下推導相應的自適應濾波算法，即SPH-ARC算法和SPW-ARC算法，并分析樣條控制點數量對自干擾對消性能的影響。最后，通過仿真實驗，對本文的算法在估計精度、收斂速度和魯棒性方面進行驗證。

1 系統模型

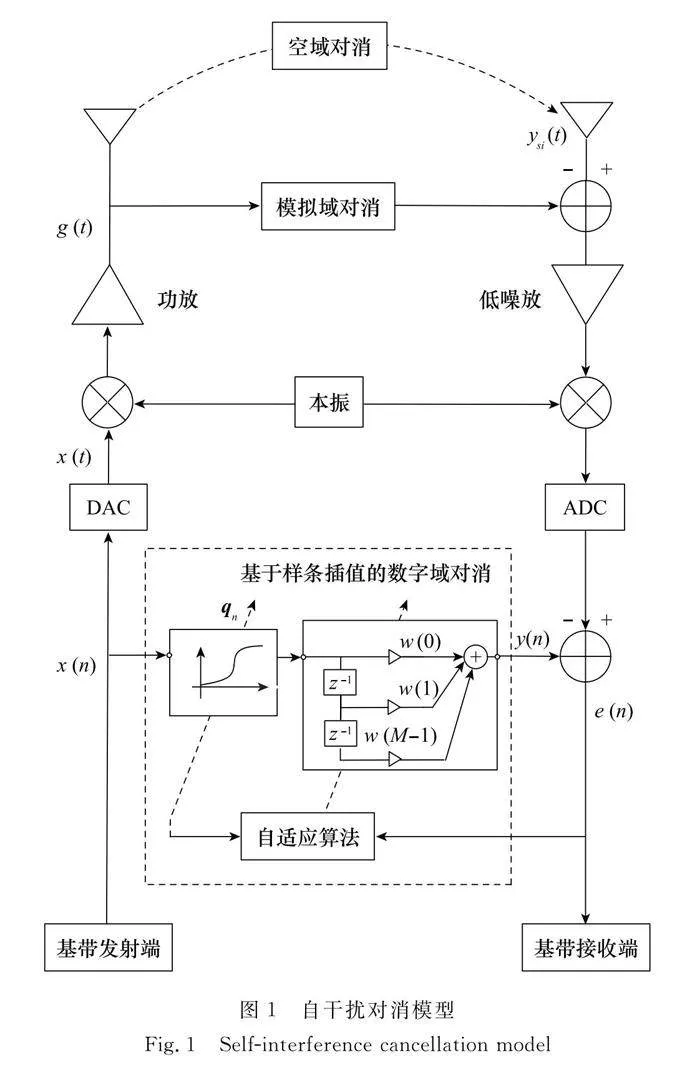
同時同頻全雙工干擾機對消模型如圖1所示。干擾機工作時發射的大功率干擾信號到達接收機形成自干擾，受現實工程中多種因素限制，經過空域、模擬域對消后，仍有部分自干擾信號殘余，為了保證整個鏈路自干擾抑制效果的最大化，在數字域對自干擾信號完成進一步的抑制。

基帶信號x（n）經過數模轉換器 （digital to analog converter， DAC）、上變頻后，通過功率放大器 （power amplifier， PA）得到射頻信號g（t），經過多徑信道后到達接收端形成自干擾信號ysi（t），d（n）是n時刻經過下變頻和模數轉換器 （analog to digital converter， ADC）后得到的接收信號，y（n）、e（n）分別是n時刻的估計信號和誤差信號。為了突出重點，假設進入數字域的信號是經空域、模擬域抑制后的。

1.1 發射信號模型

發射的寬帶信號經過功放后產生帶外頻譜展寬，需要建立描述功放特性的行為模型。在PA的行為建模中，Hammerstein模型可以看作是由無記憶非線性子塊和有記憶線性子塊級聯構成的，而Wiener模型則是將兩個子塊以相反的順序級聯［22］，兩種模型結構分別如圖2和圖3所示。

圖2和圖3中，F（·）為無記憶非線性函數，H（·）為有記憶線性函數，若Hammerstein模型中非線性子塊采用無記憶級數模型，則兩個子塊的輸出表示為

3 仿真驗證

下面對所提出的基于樣條插值對消方法性能進行驗證與評估。采用均方誤差（mean squared error， MSE）來評價算法的收斂速度、跟蹤性能與穩態誤差，采用干擾對消比（interference cancellation ratio， ICR）評價干擾對消水平。

MSE曲線能夠反應誤差信號不斷變小的過程，收斂時穩定的MSE值越小，則算法的穩態誤差越小。ICR表示對消前后自干擾抑制的程度，ICR的值越大，殘余的自干擾信號越接近系統噪聲v（n），自干擾對消的效果越好。

3.1 收斂速度與穩態誤差性能驗證

仿真條件設置如下，基帶發射信號為帶寬60 MHz的帶限高斯白噪聲，功放PA建模采用Hammerstein模型仿真，參考文獻［27］非線性子塊由樣條插值查找表LUT 實現，即q*=［－0.2，－

0.18，－0.16，…，－0.1，－0.08，－0.091，0.042，－0.001，－0.01，0.01，－0.015，0.058，0.12，0.1，0.12，…，0.18，0.2］T，線性子塊由FIR濾波器實現，即w=［0.1，0.5，0.3，－0.5，0.2］T，采樣率245 MHz，自干擾信道設置為瑞利信道，傳播路徑個數為4，信道沖激響應為h=［0.2，0.7，0.3，0.1，0］T，樣條類型選擇CR樣條，另外加入功率為-100 dB的系統噪聲。

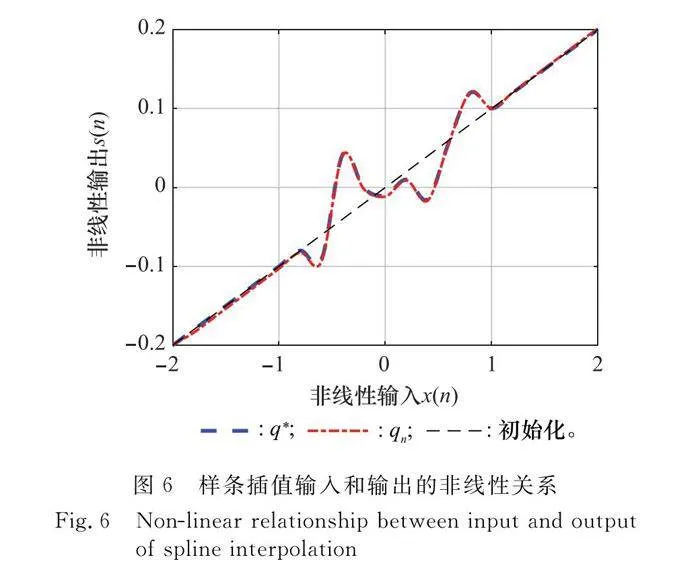
圖6描述了基帶信號x（n）和樣條插值輸出信號s（n）之間的非線性關系，其中q*曲線反映了根據查找表LUT建模時的非線性關系，收斂后的qn曲線能夠很好地與期望曲線相一致。由于Hammerstein模型中的線性FIR部分與自干擾信道是級聯的，由式（8）可知，因多徑效應帶來的影響可以通過增加記憶深度來消除，最終wn收斂后的結果是線性FIR部分w和自干擾信道h線性卷積后的值。

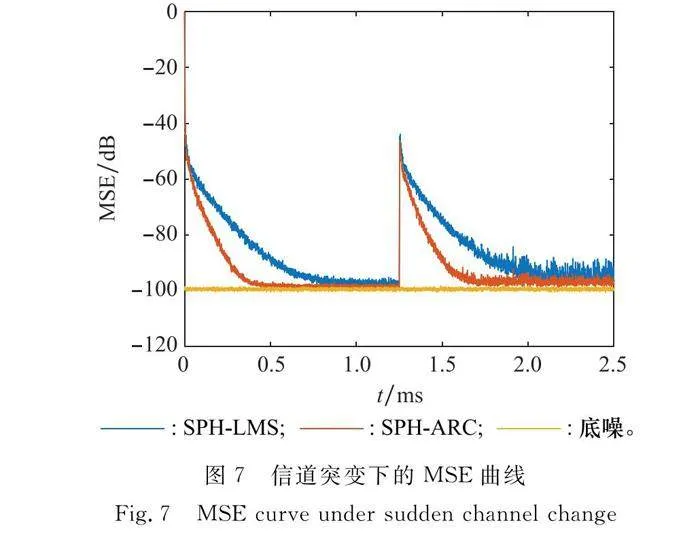
為了驗證算法在自干擾信道發生突變時的跟蹤能力，本文在仿真中間時刻1.25 ms時，自干擾信道系數向量變為原來的2倍，即h=2×［0.2，0.7，0.3，0.1，0］T，觀察算法的時變跟蹤能力。

圖7反映了算法的MSE曲線，當自干擾信道發生突變時，本文的SPH-ARC算法能夠以更快的速度完成跟蹤，相比于傳統的SPH-LMS算法，收斂速度提高了1倍。當系統采樣率為245 MHz時，SPH-ARC算法能夠在0.5 ms左右完成收斂，能夠滿足實時性的要求。另外，穩定時SPH-ARC算法能保持更低的穩態誤差，在性能方面保持更優。綜上所述，當信道未發生變化時，SPH-ARC算法能夠保持高收斂速度和低穩態誤差;當信道發生變化時，這種優勢仍然保持。

3.2 非線性對消性能

下面對比分析SPH-LMS算法和SPH-ARC算法非線性對消的性能，以對消比為評價指標，仿真條件采用第3.1節中的參數。

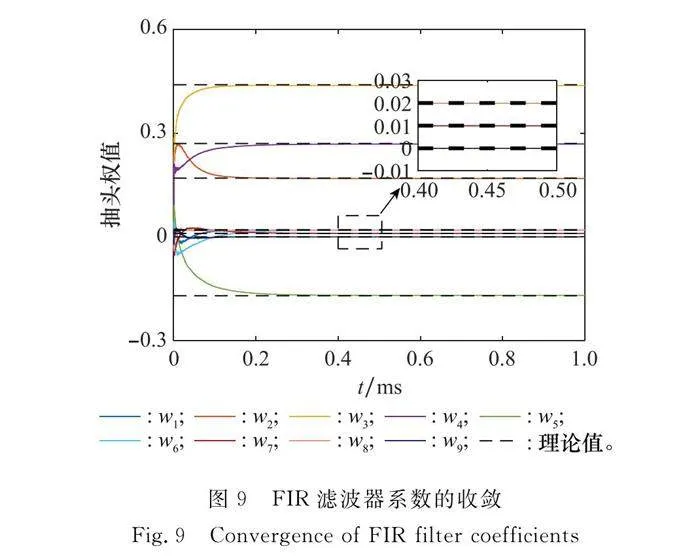
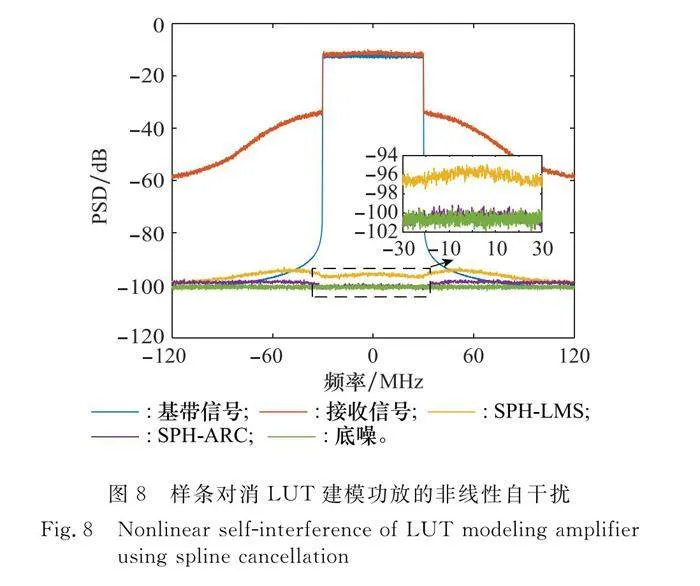
圖8為對消前及兩種算法對消后殘余干擾信號的功率譜密度（power spectral density， PSD）。由于功放非線性的存在，接收信號d（n）的功率譜出現帶外頻譜展寬。相比于對消前的自干擾信號功率譜，SPH-LMS算法未能實現完全的自干擾抑制，仍有一部分自干擾殘留;而SPH-ARC算法能夠達到將自干擾對消至底噪的抑制效果，經計算SPH-ARC算法比SPH-LMS算法對消比提升了4.2 dB。由于整個仿真鏈路中由樣條控制點組成的查找表LUT和FIR濾波器系數是已知的，即先通過樣條正向建模，再自適應求解系數完成對消。如圖9所示，最終自適應估計得到的系數與仿真設定的值幾乎保持一致，完成的ICR指標較高。

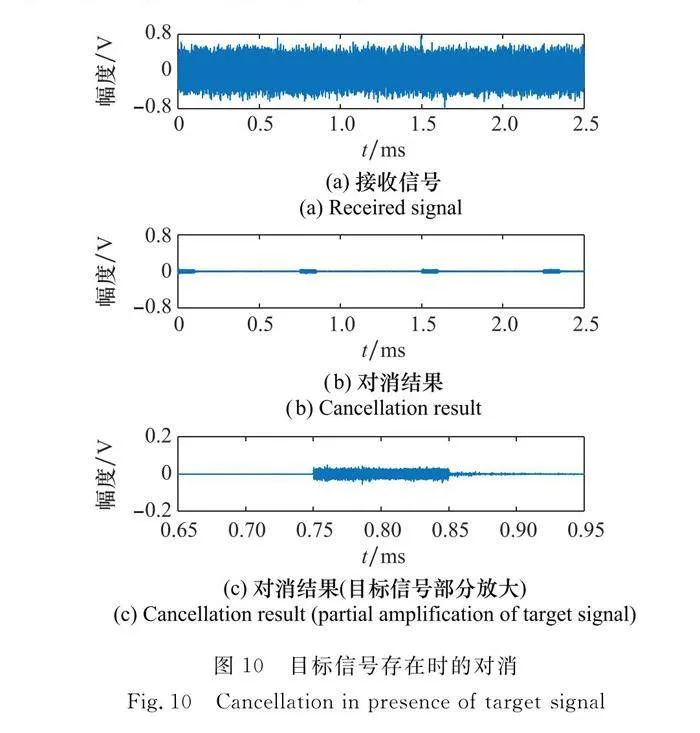
若考慮目標信號對自干擾對消性能的影響，這里假設目標信號與自干擾信號是不相關的，目標信號參數設置如下：信號類型為線性調頻 （linear frequency modulation， LFM） 脈沖信號，中心頻率30 MHz，帶寬40 MHz，脈寬100 μs，脈沖重復周期0.75 ms。

圖10所示為目標信號存在的情況下對消前后的時域波形，此時的接收信號包含了目標LFM脈沖與自干擾信號，并且目標脈沖在時域上被自干擾信號淹沒。經過非線性對消后，自干擾信號能夠得到很好地抑制，對消后殘余的是與參考信號不相關的目標脈沖。

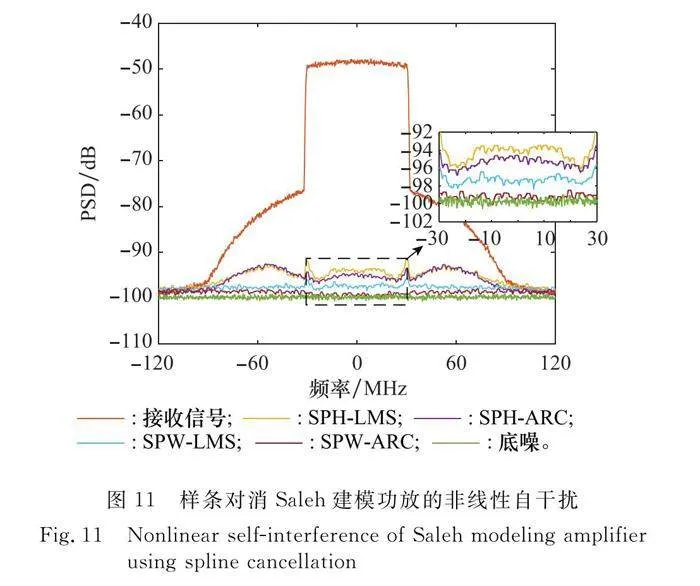
為了驗證基于樣條插值對消方法在其他功放模型下的對消性能，選用不同的功放模型完成建模。仿真參數設置如下：假設PA服從Wiener模型，分別由線性時不變（linear time invariant， LTI）系統子塊和Saleh非線性子塊組成，設定LTI線性子塊的系統函數為，H（z）=0.769 2+0.153 8z－1+0.076 9z－2，非線性子塊采用無記憶Saleh模型建模，其幅度A（r）和相位φ（r）分別滿足A（r）=（αar）/（1+βar2）和φ（r）=（αφr2）/（1+βφr2），其中αa=2.158 7，βa=1.151 7，αφ=4.003 3，βφ=9.104 0，選取的系數與文獻［28］相同。輸入信號仍為帶寬60 MHz的帶限高斯白噪聲，系統噪聲為均值為0、方差為0.001的白噪聲，干噪比為45 dB，FIR濾波器階數為5，樣條控制點由21個等間隔的數組成qn=［－2.0，－1.8，－1.6，…，1.6，1.8，2.0］T，樣條類型選擇CR樣條。

圖11所示為對消前以及4種算法對消后的自干擾信號功率譜。相比于原始自干擾信號功率譜，4種算法均實現了有效的自干擾抑制。其中，SPW模型下的SPW-ARC算法相比于SPW-LMS算法具備更好的抑制效果，同樣SPH模型下的SPH-ARC算法相比于SPH-LMS算法也能夠抵消更多的自干擾。可以看到，就SPH-LMS算法和SPH-ARC算法而言，其未能實現完全的自干擾抑制，仍有部分自干擾殘留，而利用SPW-LMS算法和SPW-ARC算法則可以有效的抑制掉殘余的自干擾。這是因為在PA建模過程中采用的是Wiener模型，在抵消時SPW模型下的算法與建模的Wiener模型更匹配，因此自干擾抑制效果會更好，抵消后的殘余信號更接近底噪。其中，SPW-LMS算法抵消后的殘余的帶內自干擾信號功率距離底噪3 dB左右，SPW-ARC算法則可以完全抵消到底噪附近，帶內對消比達到50 dB。

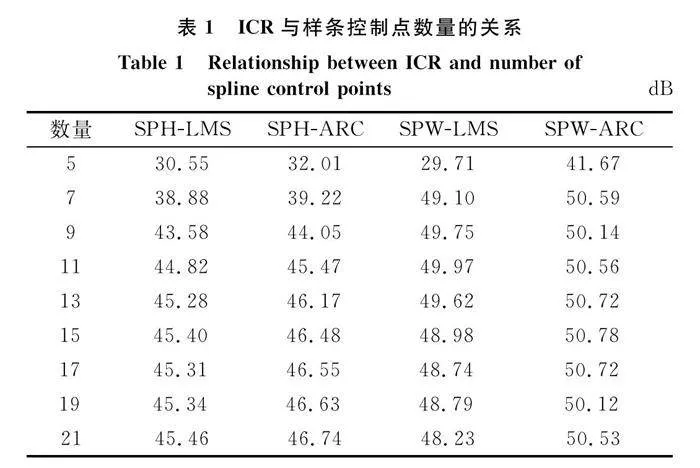
樣條控制點數量決定了系數估計的精度，從而影響自干擾抑制的性能，如果用于更新的樣條控制點qn過少，則不能達到很好的效果。表1給出了4種算法的帶內ICR與樣條控制點數量之間的關系。由于樣條基矩陣C是一個四階矩陣，根據式（12）的描述，每次迭代至少有4個樣條控制點同時參與計算，即qn的數量大于4。

當樣條控制點數量為5時，SPW-ARC算法的ICR為41.67 dB，而SPW-LMS算法的ICR僅為29.71 dB。當樣條控制點數量較少時，SPW-ARC和SPH-ARC算法相較于SPW-LMS和SPH-LMS算法ICR的優勢更加明顯。隨著樣條控制點數量的不斷增加，ICR呈現逐漸變大的趨勢。當樣條控制點數量大于13時，此時再增加樣條控制點的數量，ICR基本保持不變。當樣條控制點數量為21時，SPW-ARC算法完成的ICR指標優于SPW-LMS算法，SPH-ARC算法同樣保持這樣的優勢。因此，為了簡化計算并保證計算復雜度，選擇合適數量的樣條控制點是十分關鍵的。

3.3 存在脈沖干擾下的對消

在實際的干擾機環境中存在大量的電磁設備，背景噪聲中會伴隨有突發干擾，尤其是大幅度尖峰脈沖干擾，其分布統計特征符合典型的非高斯特性，脈沖干擾會導致最小均方樣條插值算法的性能退化。非高斯噪聲中應用最廣泛的是Alpha穩定分布模型，其特征函數［29］為

f（t）=exp{jδt－γ|t|α［1+jβsgn（t）S（t，α）］}（39）

式中：S（t，α）=tan（απ/2）， α≠1

（2/π）ln|t|， α=1;α∈（0，2］

是表示脈沖強

度的特征指標;β∈［－1，1］是對稱參數;γgt;0是色散參數;δ∈（－∞，∞）是位置參數。其中，α的值越小，代表大幅度值的脈沖出現的概率越高，當α=2時脈沖噪聲失去突發的特性，進而成為高斯噪聲。

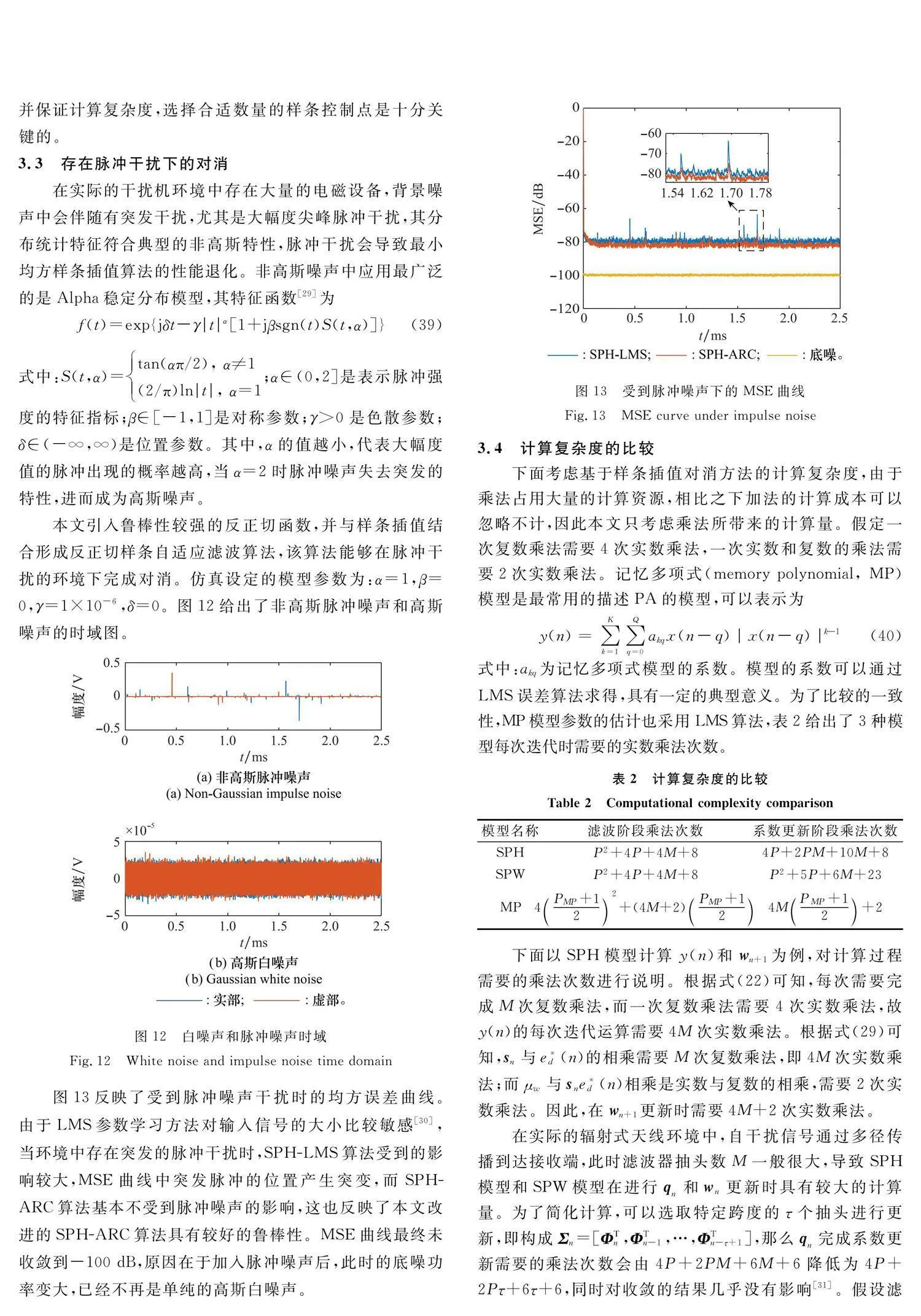
本文引入魯棒性較強的反正切函數，并與樣條插值結合形成反正切樣條自適應濾波算法，該算法能夠在脈沖干擾的環境下完成對消。仿真設定的模型參數為：α=1，β=0，γ=1×10－6，δ=0。圖12給出了非高斯脈沖噪聲和高斯噪聲的時域圖。

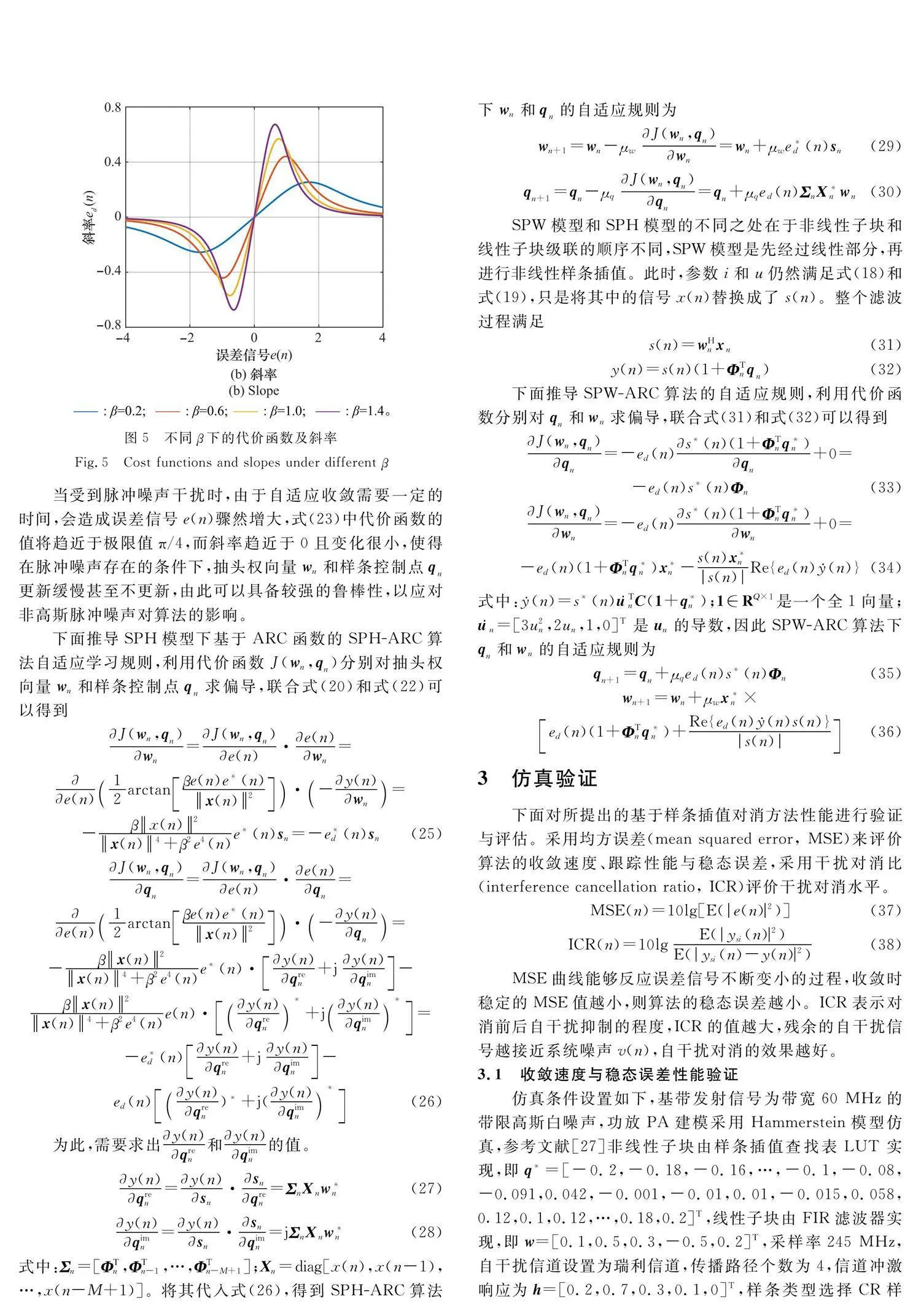
圖13反映了受到脈沖噪聲干擾時的均方誤差曲線。由于LMS參數學習方法對輸入信號的大小比較敏感［30］，當環境中存在突發的脈沖干擾時，SPH-LMS算法受到的影響較大，MSE曲線中突發脈沖的位置產生突變，而SPH-ARC算法基本不受到脈沖噪聲的影響，這也反映了本文改進的SPH-ARC算法具有較好的魯棒性。MSE曲線最終未收斂到-100 dB，原因在于加入脈沖噪聲后，此時的底噪功率變大，已經不再是單純的高斯白噪聲。

3.4 計算復雜度的比較

下面考慮基于樣條插值對消方法的計算復雜度，由于乘法占用大量的計算資源，相比之下加法的計算成本可以忽略不計，因此本文只考慮乘法所帶來的計算量。假定一次復數乘法需要4次實數乘法，一次實數和復數的乘法需要2次實數乘法。記憶多項式（memory polynomial， MP）模型是最常用的描述PA的模型，可以表示為

y（n）=∑Kk=1∑Qq=0akqx（n－q）|x（n－q）|k－1（40）

式中：akq為記憶多項式模型的系數。模型的系數可以通過LMS誤差算法求得，具有一定的典型意義。為了比較的一致性，MP模型參數的估計也采用LMS算法，表2給出了3種模型每次迭代時需要的實數乘法次數。

下面以SPH模型計算y（n）和wn+1為例，對計算過程需要的乘法次數進行說明。根據式（22）可知，每次需要完成M次復數乘法，而一次復數乘法需要4次實數乘法，故y（n）的每次迭代運算需要4M次實數乘法。根據式（29）可知，sn與e*d（n）的相乘需要M次復數乘法，即4M次實數乘法;而μw與sne*d（n）相乘是實數與復數的相乘，需要2次實數乘法。因此，在wn+1更新時需要4M+2次實數乘法。

在實際的輻射式天線環境中，自干擾信號通

過多徑傳播到達接收端，此時濾波器抽頭數M一般很大，導致SPH模型和SPW模型在進行qn和wn更新時具有較大的計算量。為了簡化計算，可以選取特定跨度的τ個抽頭進行更新，即構成Σn=［ΦTn，ΦTn－1，…，ΦTn－τ+1］，那么qn完成系數更新需要的乘法次數會由4P+2PM+6M+6降低為4P+2Pτ+6τ+6，同時對收斂的結果幾乎沒有影響［31］。假設濾波器抽頭數M=76，樣條階數P=2，MP模型的非線性階數為PMP=11，SPH模型在系數更新時，qn和wn自適應迭代需要的乘法次數分別為774和306，而MP模型則需要1 826次實數乘法，這對算法的實時性提出了巨大的挑戰。對于濾波過程，MP模型需要的實數乘法次數為1 980，而基于樣條插值的SPH 模型和SPW模型僅需要324次的實數乘法，可以減少83%的計算度。

另外，針對干擾機所處的環境而言，發射鏈路PA的非線性可以認為保持恒定，當自干擾信道發生變化時，只需要對濾波器系數wn進行自適應更新即可，而不需要進行樣條控制點qn的更新，進一步降低了計算復雜度。

4 結 論

本文采用基于樣條插值的數字對消方法用于解決干擾機中由于功放非線性導致的非線性自干擾問題，在樣條查找表LUT和自適應濾波基礎上，分別針對SPW模型和SPH模型設計了魯棒性更強的SPW-ARC算法和SPH-ARC算法。仿真結果表明，本文改進的算法能有效提升收斂速度并且改善穩態誤差性能，在信道突變的場景下跟蹤性能更好。同時，也克服了由于傳統SPW-LMS算法和SPH-LMS算法對輸入信號敏感，導致脈沖噪聲干擾場景下性能惡化的問題。

對Hammerstein模型建模的PA，相比于SPH-LMS算法，本文的SPH-ARC算法收斂速度提高了1倍，ICR也獲得了4 dB左右的提升。對Wiener模型的PA，SPW-ARC算法相較于SPW-LMS算法對消比提升了3 dB左右。因此，將本文方法應用于非線性自干擾對消領域中具有一定的應用價值。

參考文獻

［1］ GE S H， XING J L， LIU Y C， et al. Dual-stage co-site RF interference canceller for wideband direct-conversion receivers using reduced observation chain［J］. IEEE Trans.on Electromag-netic Compatibility， 2020， 62（3）： 923-932.

［2］ HONG Z H， ZHANG L， LI W， et al. Frequency-domain RF self-interference cancellation for in-band full-duplex communications［J］. IEEE Trans.on Wireless Communications， 2023， 22（4）： 2352-2363.

［3］ MORI S， MIZUTANI K， HARADA H. Digital self-interference cancellation scheme for full-duplex cellular system in 5G［C］∥Proc.of the IEEE 33rd Annual International Symposium on Personal， Indoor and Mobile Radio Communications， 2022： 1165-1170.

［4］ ZHANG Y， LIU J， ZHOU H F. One novel method of complex direct wave suppression based on CLEAN technology［C］∥Proc.of the IEEE International Symposium on Phased Array System amp; Technology， 2019.

［5］ SHEN L， HENSON B， ZAKHAROV Y， et al. Digital self-interference cancellation for full-duplex underwater acoustic systems［J］. IEEE Trans.on Circuits and Systems II： Express Briefs， 2020， 67（1）： 192-196.

［6］ FICIU I D， STANCIU C L， ELISEI-ILIESCU C， et al. Low-complexity implementation of a data-reuse RLS algorithm［C］∥Proc.of the 45th International Conference on Telecommunications and Signal Processing， 2022： 289-293.

［7］ DU Y Q， CHEN J H， LI G H， et al. Integrated self-interference suppression for single antenna full-duplex without circulator［C］∥Proc.of the IEEE 20th Interregional NEWCAS Conference， 2022： 75-79.

［8］ 何方敏， 李毅， 孟進， 等. 基于導頻的同頻噪聲干擾對消技術［J］. 系統工程與電子技術， 2020， 42（5）： 992-998.

HE F M， LI Y， MENG J， et al. Pilot-aided cancellation technology for co-frequency noise interference［J］. Systems Engineering and Electronics， 2020， 42（5）： 992-998.

［9］ LUO Y J， BI L H， ZHAO D. Adaptive digital self-interference cancellation based on fractional order LMS in LFMCW radar［J］. Journal of Systems Engineering and Electronics， 2021， 32（3）： 573-583.

［10］ MORI S， MIZUTANI K， HARADA H. A digital self-interference cancellation scheme for in-band full-duplex-applied 5G system and its software-defined radio implementation［J］. IEEE Open Journal of Vehicular Technology， 2023， 4： 444-456.

［11］ KONG D H， KIL Y S， KIM S H. Neural network aided digital self-interference cancellation for full-duplex communication over time-varying channels［J］. IEEE Trans.on Vehicular Technology， 2022， 71（6）： 6201-6213.

［12］ HUANG X， LE A T， GUO Y J. Joint analog and digital self-interference cancellation for full duplex transceiver with frequency-dependent I/Q imbalance［J］. IEEE Trans.on Wireless Communications， 2023， 22（4）： 2364-2378.

［13］ FUKUI T， KOMATSU K， MIYAJI Y， et al. Analog self-interference cancellation using auxiliary transmitter considering IQ imbalance and amplifier nonlinearity［J］. IEEE Trans.on Wireless Communications， 2020， 19（11）： 7439-7452.

［14］ MOHAMMADIAN A， TELLAMBURA C， VALKAMA M. Analysis of self-interference cancellation under phase noise， CFO， and IQ imbalance in GFDM full-duplex transceivers［J］. IEEE Trans.on Vehicular Technology， 2020， 69（1）： 700-713.

［15］ YAO Y， JIN Y， LI M Y， et al. An accurate three-input nonlinear model for joint compensation of frequency-dependent I/Q imbalance and power amplifier distortion［J］. IEEE Access， 2019， 7： 140651-140664.

［16］ ERDEM M， AYAR H， NAWAZ H， et al. Monostatic antenna in-band full duplex radio： performance limits and characterization［J］. IEEE Trans.on Vehicular Technology， 2019， 68（5）： 4786-4799.

［17］ GUO W Y， ZHI Y F. Nonlinear spline Versoria prioritization optimization adaptive filter for alpha-stable clutter［J］. IEEE Trans.on Aerospace and Electronic Systems， 2023， 59（1）： 734-744.

［18］ 管鵬鑫， 汪奕汝， 趙玉萍. 基于正則化的全雙工通信系統非線性自干擾消除方法［J］. 北京大學學報（自然科學版）， 2021， 57（6）： 991-996.

GUAN P X， WANG Y R， ZHAO Y P. A regul-arization based nonlinear self-interference suppression method for full duplex communication systems［J］. Acta Scientiarum Naturalium Universitatis Pekinensis， 2021， 57（6）： 991-996.

［19］ ERDEM M， OZKAN H， GURBUZ O. A new online nonlinear self-interference cancelation method with random fourier features［J］. IEEE Wireless Communications Letters， 2022， 11（7）： 1379-1383.

［20］ 崔中普， 葛松虎， 李亞星， 等. 基于二維正交化WLCLMS的自干擾對消方法［J］. 系統工程與電子技術， 2022， 44（9）： 2726-2735.

CUI Z P， GE S H， LI Y X， et al. Two-dimensional orthogonalization WLCLMS scheme for self-interference cancellation［J］. Systems Engineering and Electronics， 2022， 44（9）： 2726-2735.

［21］ 路雷， 褚建軍， 唐燕群， 等. 基于卷積長短時記憶深度神經網絡的帶內全雙工非線性數字自干擾消除［J］. 電子與信息學報， 2022， 44（11）： 3874-3881.

LU L， CHU J J， TANG Y Q， et al. Driven non-linear digital self interference cancellation for in-band full duplex systems based on convolution long short-term memory deep neural network［J］. Journal of Electronics amp; Information Technology， 2022， 44（11）： 3874-3881.

［22］ GHANNOUCHI F M， HAMMI O. Behavioral modeling and predistortion［J］. IEEE Micro-wave Magazine， 2009， 10（7）： 52-64.

［23］ 全欣， 劉穎， 范平志， 等. 一種抑制相位噪聲的多通道變時延下變頻全雙工收發方法［J］. 電子與信息學報， 2023， 45（5）： 1627-1634.

QUAN X， LIU Y， FAN P Z， et al. A multiple-downconversion full-duplex transceiver design for phase noise suppression［J］. Journal of Electronics amp; Information Technology， 2023， 45（5）： 1627-1634.

［24］ SCARPINITI M， COMMINIELLO D， PARISI R， et al. Nonlinear spline adaptive filtering［J］. Signal Processing， 2013， 93（4）： 772-783.

［25］ LIU C， ZHANG Z， TANG X. Steady-state performance for the sign normalized algorithm based on Hammerstein spline adaptive filtering［C］∥Proc.of the International Conference on Control， Automation and Information Sciences， 2019.

［26］ CAMPO P P， KORPI D， ANTTILA L， et al. Nonlinear digital cancellation in full-duplex devices using spline-based Hammerstein model［C］∥Proc.of the IEEE Globecom Workshops， 2018.

［27］ SCARPINITI M， COMMINIELLO D， PARISI R， et al. Hammerstein uniform cubic spline adaptive filters： learning and convergence properties［J］. Signal Processing， 2014， 100： 112-123.

［28］ SALEH A A M. Frequency-independent and frequency-depen-dent nonlinear models of twt amplifiers［J］. IEEE Trans.on Communications， 1981， 29（11）： 1715-1720.

［29］ YANG L D， LIU J， YAN R Q， et al. Spline adaptive filter with arctangent-momentum strategy for nonlinear system identification［J］. Signal Processing， 2019， 164： 99-109.

［30］ 劉郁林. 自適應濾波算法與實現［M］. 4版. 北京： 電子工業出版社， 2014.

LIU Y L. Adaptive filtering： algorithms and practical implementation［M］. 4th ed. Beijing： Electronic Industry Press， 2014.

［31］ CAMPO P P， ANTTILA L， KORPI D， et al. Cascaded spline-based models for complex nonlinear systems： methods and applications［J］. IEEE Trans.on Signal Processing， 2021， 69： 370-384.

作者簡介

趙忠凱（1979—），男，副教授，博士，主要研究方向為雷達偵察與干擾、寬帶信號檢測與識別。

關澤越（1998—），男，碩士研究生，主要研究方向為雷達干擾機自干擾對消。

李 虎（1986—），男，高級工程師，博士，主要研究方向為雷達電子對抗。