基于信干噪比最大化的盲提取抗主瓣干擾方法

摘 要：

針對雷達主瓣干擾抑制問題，提出一種基于信干噪比（signal to interference plus noise ratio， SINR）最大化的盲提取主瓣干擾抑制方法。與盲分離不同，盲提取能夠從多路混合信號中提取出感興趣的一路分量，這更適合在多信源多通道的復雜電磁環境下進行干擾抑制。該方法在混合信號距離域建立SINR最大化的優化模型，采用粒子群優化（particle swarm optimization， PSO）算法進行求解并提取出目標回波信號實現主瓣干擾抑制。經仿真測試，該方法相較于傳統的盲分離干擾抑制方法，提升了干擾抑制效果;無需信源數目估計，對通道數目要求更低，在欠定場景中依然適用;減小了計算復雜度，更適用于復雜電磁環境。

關鍵詞：

雷達抗干擾; 主瓣干擾抑制; 盲提取; 粒子群優化算法

中圖分類號：

TN 974

文獻標志碼： A""" DOI：10.12305/j.issn.1001-506X.2024.09.09

Anti-mainlobe jamming method via blind extraction based on maximizing SINR

YU Lei1，2， LIU Yipin1，2，*， WEI Yinsheng1，2

（1. School of Electronics and Information Engineering， Harbin Institute of Technology， Harbin 150001， China;

2. Key Laboratory of Marine Environmental Monitoring and Information Processing， Ministry of Industry

and Information Technology， Harbin 150001， China）

Abstract：

Regarding the suppression of radar mainlobe jamming， a blind extraction method for suppressing mainlobe jamming based on maximizing the signal to interference plus noise ratio （SINR） is proposed. Unlike blind separation， blind extraction can extract interested components from multiple mixed signals， making it more suitable for jamming suppression in complex electromagnetic environments with multiple sources and channels. This method establishes an optimization model for maximizing SINR in the distance domain. The target echo signal is solved and extracted using the particle swarm optimization （PSO） algorithm to achieve mainlobe jamming suppression. Simulation testing shows that the proposed method improves the jamming suppression effect compared to traditional blind separation jamming suppression methods. It does not require estimation of the number of sources and has lower requirements for the number of channels， making it applicable in underdetermined scenarios. Additionally， it reduces computational complexity， making it more suitable for complex electromagnetic environments.

Keywords：

radar anti-jamming; mainlobe jamming suppression; blind extraction; particle swarm optimization （PSO） algorithm

0 引 言

隨著電子對抗技術的發展，雷達接收的信號除了目標信號還包含對方釋放的電子干擾。其中，對于主瓣干擾，傳統的信號處理方法很難進行濾除。作為現代信號處理的重要分支，盲信號分離是指在沒有源信號和信道參數先驗信息的前提下，只依靠接收器接收到的混合信號分離出源信號。其代表性算法有特征矩陣聯合近似對角化（joint approximate diagonalization of eigen matrices， JADE）算法［1］、快速獨立成分分析（fast independent component analysis， FastICA）算法［2］等。由于盲信號分離模型與陣列信號接收模型相匹配且具備盲處理的能力，即不需要干擾信號先驗知識，因此盲分離方法已經成為雷達主瓣干擾抑制的主流方法之一。在近年來的研究中，文獻［3］結合子陣結構以及稀疏理論利用盲分離進行主瓣干擾抑制;文獻［4］提出一種基于魯棒白化預處理的盲分離干擾抑制方法;文獻［5］利用信號的極化域信息進行盲分離;此外還結合空時多通道處理［6］、深度學習［7］的干擾抑制算法。盲分離算法及其改進已經在雷達主瓣干擾抑制中得到廣泛應用［8-12］。

在現代雷達所面臨的復雜電磁環境下，空間中源信號數目較多，且受限于載體本身，雷達天線接收通道數有限，上述基于盲分離的干擾抑制方法在實際應用中存在一些問題。首先，傳統盲分離算法不能在接收通道數目小于源信號數目時對混合信號進行分離，這是因為此時為欠定問題，混合矩陣不滿足列滿秩的條件。信源數目小于等于接收通道數目是盲信號分離的基本假設之一，這限制了盲分離方法的適用范圍。其次，盲分離的前提是知道信源數目，基于盲分離的干擾抑制算法往往需要進行信源數目估計，而信源數目估計存在的誤差會直接影響到盲分離的效果［13］，這導致使用盲分離進行干擾抑制往往輸出達不到預期信干噪比。另外，混合信號中有用的分量往往只有目標回波，而盲分離算法會同時將所有源信號分離出來，其中大多數運算量都花費在了計算干擾分量中，當信源數目較大時盲分離算法將消耗巨大的運算資源和存儲資源。此外，盲分離干擾抑制方法雖然對輸入信干比不敏感，但受輸入信噪比影響較大，即向每個陣元接收信號中夾雜噪聲會嚴重影響分離效果。

盲信號提取是盲信號分離的一種特殊實現途徑，能夠逐個地、按一定順序提取源信號。當混合信號中只對部分信號感興趣時，可通過盲提取進行逐一獲得。比較成熟的盲提取算法有基于負熵等統計量的逐步提取算法［14-16］，這類算法相當于在盲分離時加入約束條件，使得算法收斂到分離出感興趣的某種類型信號。也有基于線性預測器［17］和非線性預測器［18］的提取算法，主要利用了源信號的在線預測性。此外，還有基于目標源信號特殊時間結構先驗知識的提取算法［19］，這類方法適用性強，應用廣泛。目前，盲提取已經在數學［20］、聲學［21］、醫學［22］機械［23］等多個領域得到充分應用［24-27］。

文獻［28-29］提出混沌信號的盲提取算法，根據所提取信號的特點構建了目標函數并分別采用人工蜂群算法和粒子群優化算法進行求解，達到了預期效果。文獻［30］利用目標信號的時間結構以及先驗知識，實現任意占空比數字信號位同步時鐘盲提取。文獻［31］結合低秩矩陣分析和秩約束空間，提出一種新的盲語音提取方法。這些研究成果表明，通過利用提取信號的特性選取合適的目標函數，采用智能優化算法進行求解能夠實現盲提取。在雷達領域，文獻［32］提出基于盲提取的雷達信號分選，并給出盲提取用于干擾抑制的可行性;文獻［33-34］采用基于線性預測的盲提取分別用于雜波抑制以及目標檢測，而基于盲提取的主瓣干擾抑制的研究并不多。

針對盲分離方法在雷達主瓣干擾抑制中存在的問題，本文結合雷達信號特性與盲提取理論，提出了一種基于最大化信干噪比的雷達信號盲提取主瓣干擾抑制方法。該算法能夠從接收混合信號中直接提取出目標回波信號，減小了運算資源的使用，且抑制后信干噪比更高，受噪聲的影響更低，對盲分離無法解決的欠定場景依然有效。本文首先建立信號模型，對問題進行簡要描述，其次給出了主瓣干擾抑制的核心算法，最后在仿真場景下進行算法有效性驗證并與現有盲分離算法進行對比。

1 抗主瓣干擾信號模型

考慮雷達接收天線為一維均勻線陣，陣元數目為M，陣元間距為d。雷達發射信號復包絡為線性調頻脈沖，表示為

3 算法驗證

3.1 抗干擾有效性驗證

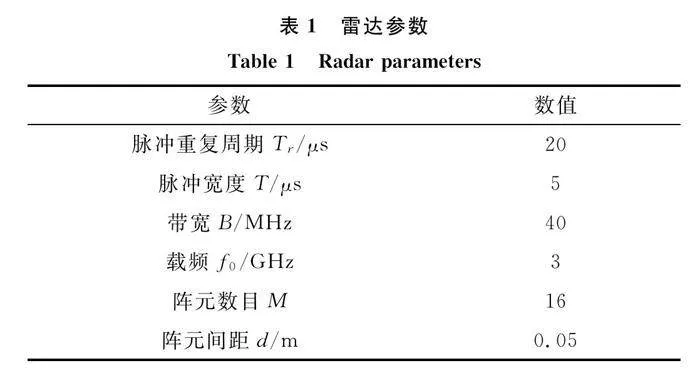
為了說明本文方法對于雷達主瓣干擾抑制的有效性，采取線性調頻體制雷達進行了主瓣干擾抑制仿真實驗，接收天線陣采用均勻直線陣。陣元配置與信號仿真參數如表1所示。

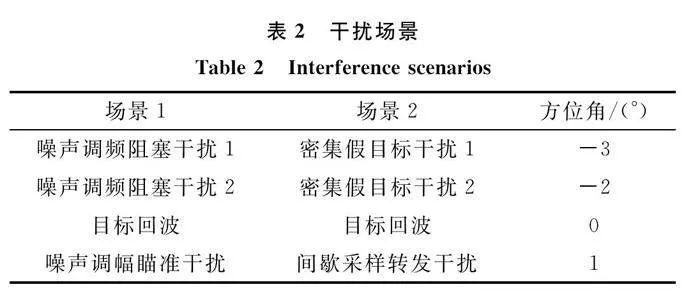
考慮了兩種干擾場景，每個場景中含有一個目標回波信號以及3個不同角度的主瓣干擾信號。分別為場景1主瓣壓制干擾場景、場景2主瓣欺騙干擾場景，如表2所示。

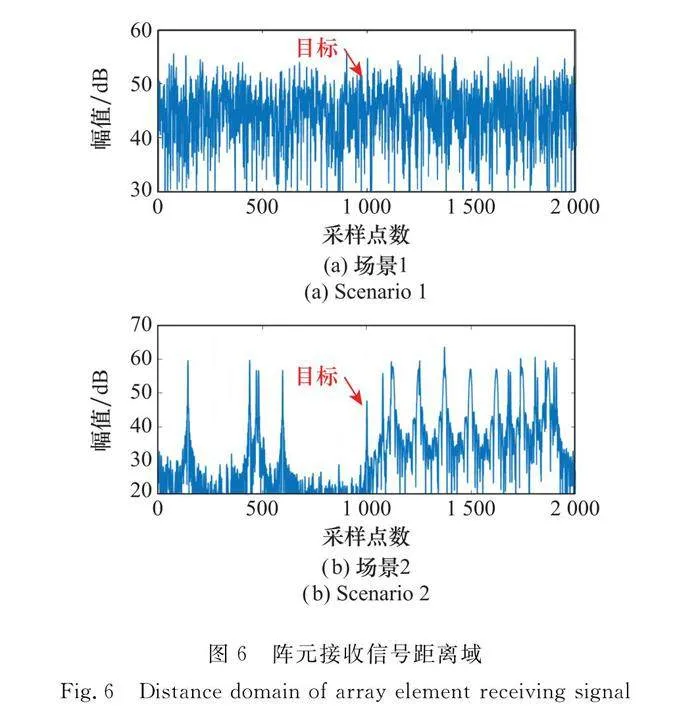
兩場景的目標回波分別于901和1 001距離單元處。通過調整噪聲與干擾信號功率，設置兩種場景脈壓前信噪比為10 dB，脈壓前信干比分別為-30 dB、-20 dB，得到場景1與場景2某單個陣元接收信號距離域即干擾抑制前距離域數據，如圖6所示。可見兩種場景下目標被完全淹沒。

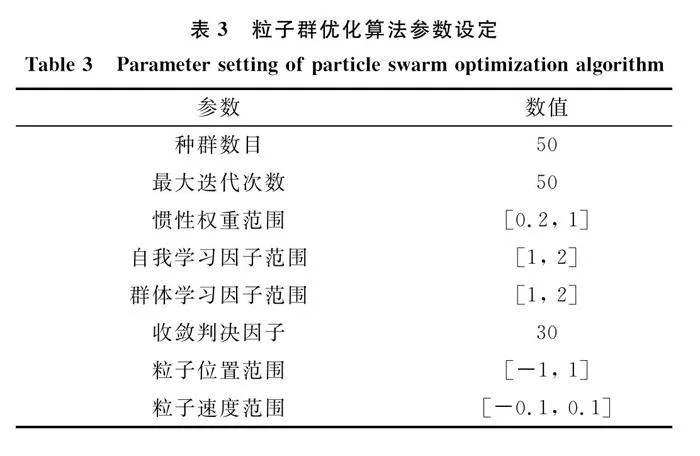
將16路混合信號距離域進行盲提取，設置盲提取算法中粒子群優化步驟的相關參數如表3所示。

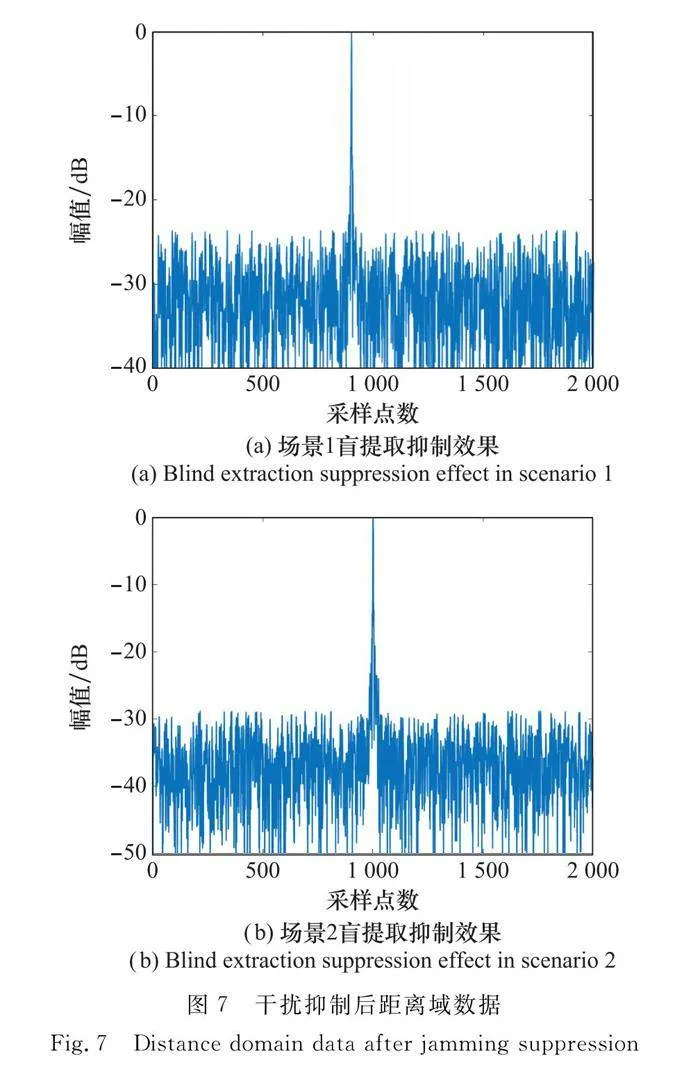
盲提取系統輸出提取信號經歸一化后如圖7所示。

可見，兩種場景提取信號得到了目標分量，脈壓后信干噪比分別達到了25 dB與30 dB，即含主瓣干擾的接收信號經盲提取系統后干擾得到了抑制。

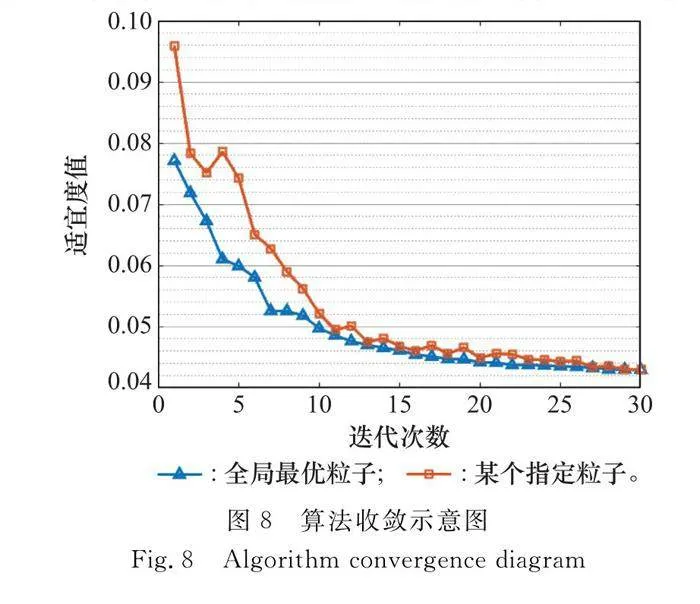
首先，測試算法的收斂速度。本文的盲提取算法核心為通過粒子群優化得到提取矢量w，其收斂速度直接關系到算法的效率。此外，在對粒子群優化算法的最大迭代次數以及種群數目等參數的設置中，也需要對算法收斂效果進行分析，選擇兼顧收斂效果和收斂時間的參數。以場景1為例，在干擾抑制的過程中記錄隨著迭代次數增加，全局最優粒子的適宜度與某個指定粒子的適宜度，繪制其變化曲線如圖8所示。

可見，隨著迭代的進行，種群中的全局最優粒子的適宜度迅速下降，在25次迭代后即收斂。而對于某個特定的粒子，由于需要跳出局部最優解，其適宜度偶見上升，在迭代次數25次時已經收斂。這表明采用粒子群優化算法計算最優分離矢量具有較快的收斂速度。此外，特定粒子最終其適宜度值與全局最優粒子適宜度值相近，這說明經過優化后所有粒子都聚集在了最優值附近。

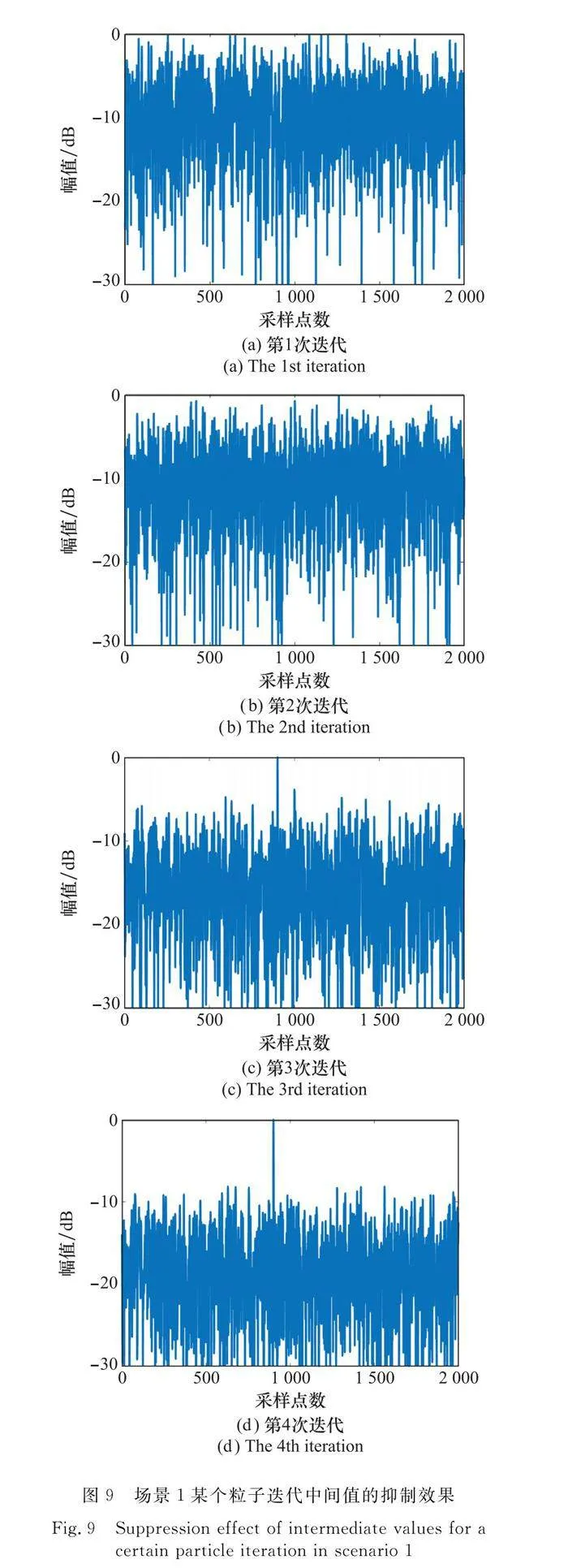
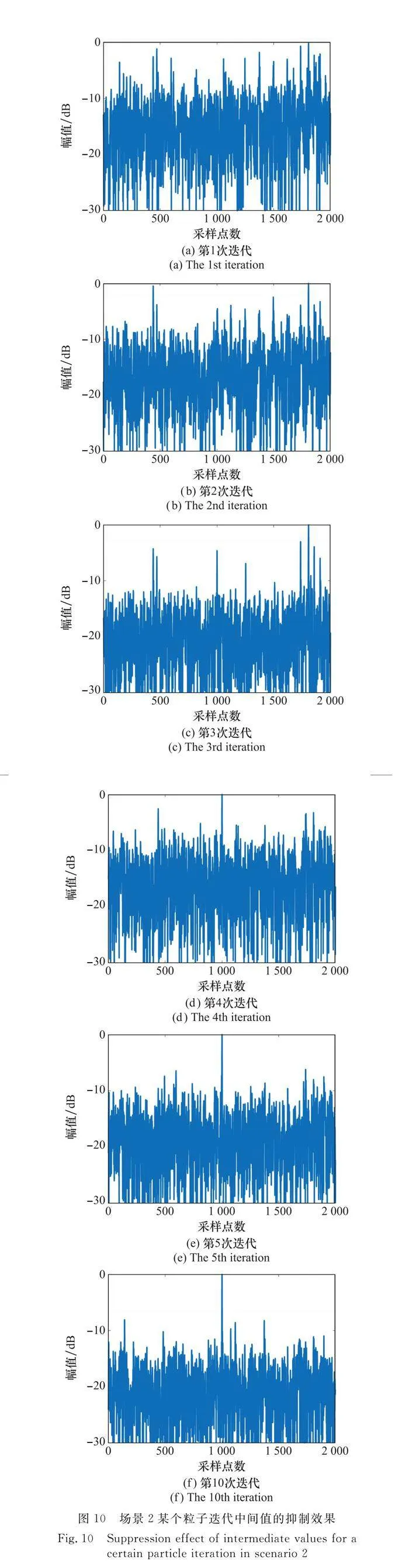
其次，測試算法的收斂精度，即測試采用式（19）所定義的目標函數能否將提取矢量收斂到提取出目標回波信號而不是其他的局部最優解。在干擾抑制的過程中記錄每次迭代得到的提取矢量，繪制其對應的提取信號，分別對場景1和場景2得到一組隨著迭代次數增加提取信號的變化，如圖9和圖10所示。

可見，對于壓制和欺騙兩類干擾，在迭代初期提取信號峰值并不是目標位置。但隨著迭代的逐步進行，提取矢量經過自我學習與群體學習逐漸向全局最優靠攏，目標位置迅速顯露，并被鎖定為峰值，從而進行進一步的優化消除干擾。

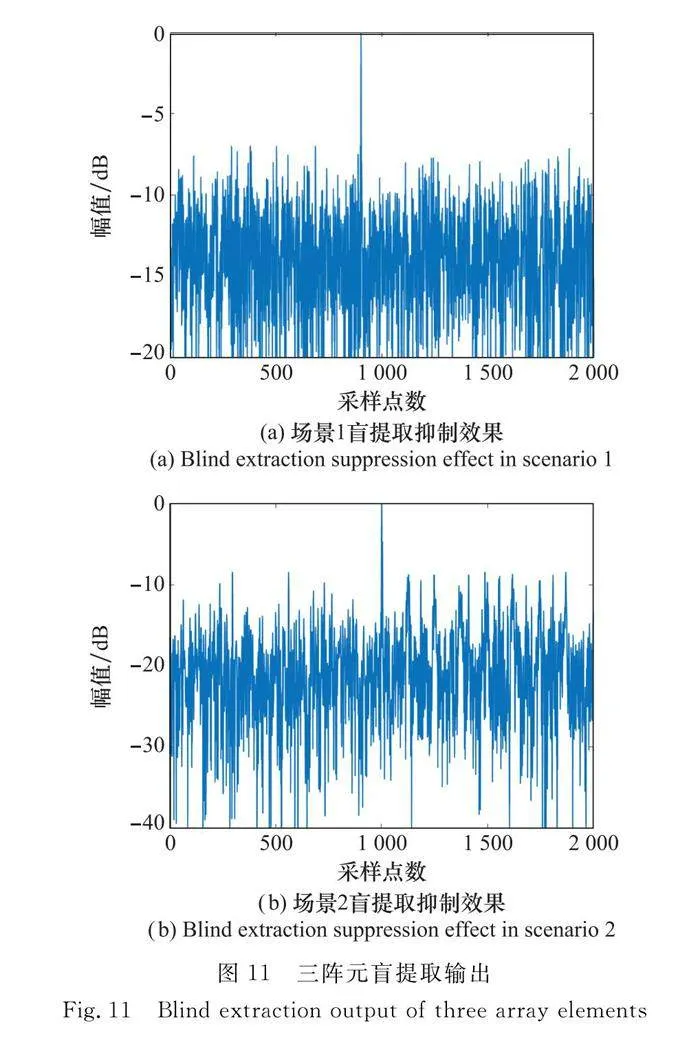
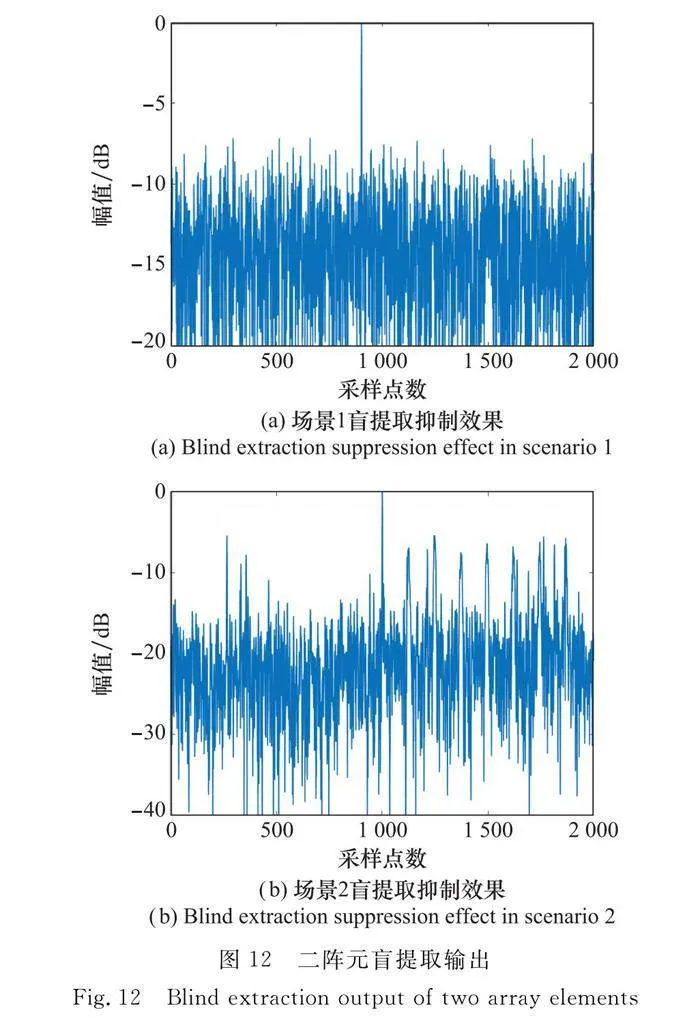
下面檢驗本方法在欠定條件下的性能，由于兩種場景信源數目為4，將上述兩種場景中陣元數目減少為3和2，分別進行盲提取干擾抑制，輸出分別如圖11和圖12所示。

可見，當陣元數目小于信源數目時，盲提取依然能夠對主瓣干擾起到抑制效果。對于接收陣元數目為3時，兩場景的輸出脈壓后信干噪比約為8 dB，對于接收陣元數目為2的極端場景，其輸出的脈壓后信干噪比依然能大于5 dB。這表明本算法在欠定場景中依然適用。

3.2 算法性能對比

在主瓣干擾抑制中應用較為廣泛的盲分離方法有Fast-ICA算法和JADE算法，這些算法都具有魯棒性高、運算速度快等優點。本節針對相同的距離域數據，利用本文的盲提取算法與這兩種傳統盲分離方法進行干擾抑制，分別從改變接收通道數目、輸入信噪比以及改變干擾入射方位角方面分析干擾抑制效果，并對比了3種算法的運算復雜度，驗證了盲提取方法的優越性。

3.2.1 抗干擾效果隨接收通道數目變化分析

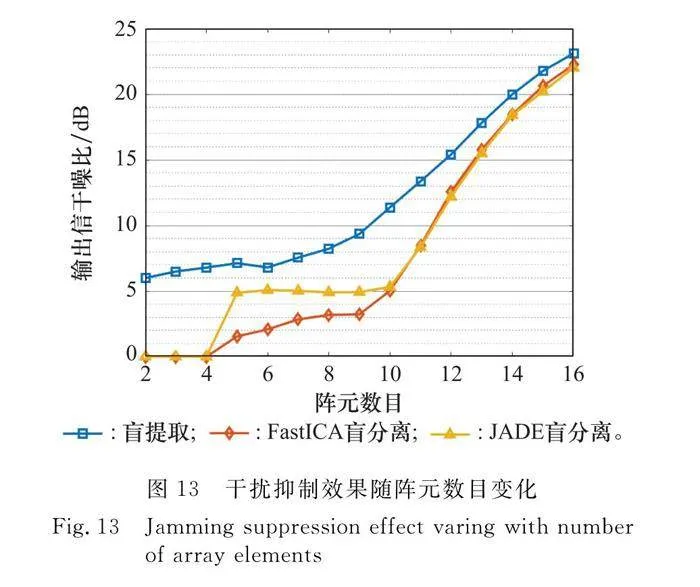
以場景1為例，對比本文盲提取算法與現有盲分離算法的干擾抑制效果。設置陣元數目范圍為2～16，對每個陣元數目下的接收信號同時進行盲提取與盲分離，并做100次蒙特卡羅模擬，統計干擾抑制輸出信干噪比，得到3種方法的干擾抑制效果，即輸出信干噪比隨陣元數目變化，如圖13所示。

可見，本文的盲提取算法干擾抑制效果優于傳統盲分離算法，在本場景下其脈壓后輸出信干噪比相較于盲分離最高可達8 dB。隨著陣元數目的減少，傳統盲分離算法抑制效果下降更明顯。當陣元數目減少到小于信源數目時，傳統盲分離算法無法運行而盲提取仍能夠有效地抑制干擾。

3.2.2 干擾抑制效果隨輸入信噪比變化分析

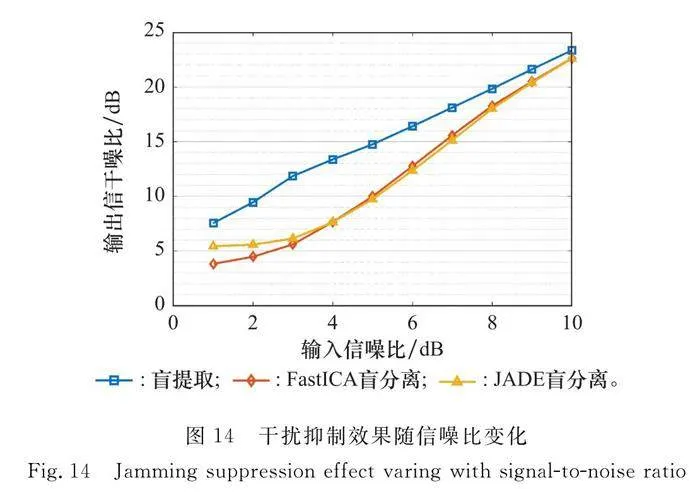
在眾多盲分離算法中，低信噪比下分離性能急劇下降是一個普遍存在的問題。以場景1為例，控制陣列接收時的噪聲功率使脈壓前信噪比變化范圍為1～10 dB，每個信噪比等級分別進行100次蒙特卡羅模擬，以輸出信干噪比來衡量干擾抑制效果，最終得到兩種算法的脈壓后輸出信干噪比隨輸入信噪比的變化，如圖14所示。

可見，在本場景中，當接收機信噪比較高時，盲提取與盲分離方法的干擾抑制效果相近。而隨著信噪比的降低，盲分離算法干擾抑制效果相較于盲提取下降迅速，即傳統盲分離算法相較于所提盲提取算法對噪聲更加敏感。在相同的輸入信噪比下，盲提取算法相較于傳統盲分離算法，干擾抑制效果提升最高可達7 dB。

3.2.3 干擾抑制效果隨方位角變化分析

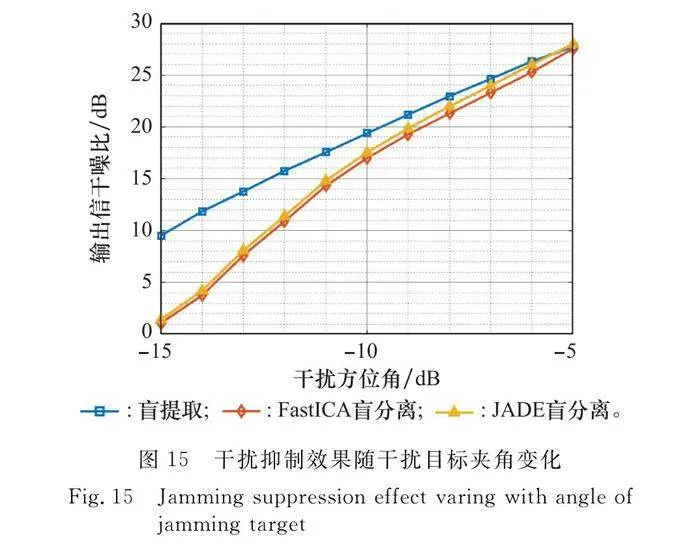
為了簡化分析干擾抑制效果隨干擾與目標方位角夾角的影響，將場景設置為只含有一個干擾和目標，脈壓前信干比、信噪比分別為-20 dB、10 dB，接收陣元數目為8。為了便于觀察，將角度取對數并乘10，類似于dB來表示，即0 dB表示1°，-10 dB表示0.1°。目標方位角恒為0°，控制干擾方位角以對數逐級遞減，每個角度分別做100次蒙特卡羅模擬，得到3種算法輸出信干噪比隨干擾方位角變化示意圖，如圖15所示。

可見，3種算法隨著干擾的方位角與目標逐漸接近，抑制效果都有所下降。而相對來說，本文提出的盲提取算法下降的速率更慢。例如，圖15中該場景下對于相同的脈壓后輸出信干噪比10 dB，傳統方法所能承受的最小方位角約為盲提取方法所能承受的最小方位角的2倍。

3.2.4 計算復雜度分析

本文提出的盲提取算法，其計算復雜度主要體現在粒子群優化求解提取矢量w的過程中。設接收信號通道個數為m，每路信號采樣點數為l，粒子群優化設定種群數目為N，迭代次數為n。每輪迭代的主要運算量為計算每個粒子的適宜度值，經計算其復雜度為O（Nml），則算法總體復雜度表示為

T1≈O（Nnml）（26）

對于傳統的盲分離算法，經計算，JADE算法的計算復雜度近似為

T2≈O（m4l）+O（m6）+O（m2g）≈O（m4l）（27）

式中：g為聯合對角化過程中Givens旋轉法迭代次數。此外，FastICA算法計算復雜度近似為

T3≈O（km2l）+O（km3）≈O（km2l）（28）

式中：k為迭代優化使負熵最小的迭代次數。

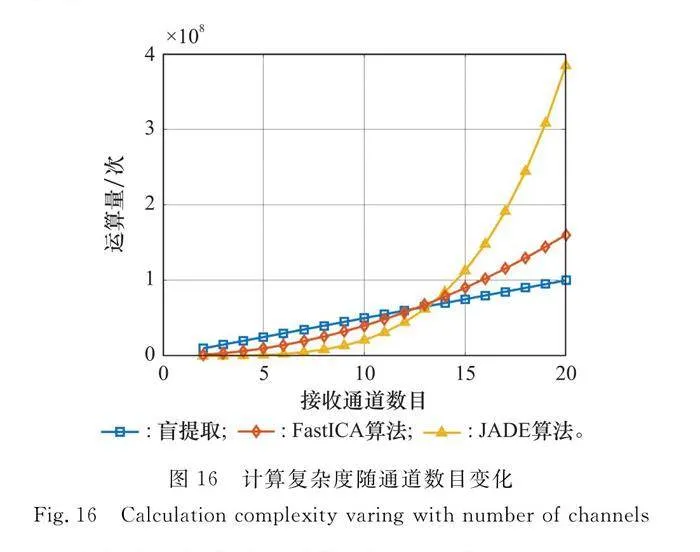
可見，盲提取的計算復雜度正比于通道數目m，而傳統盲分離算法其計算復雜度正比于m2、m4。設信號采樣點數l=2 000，繪制出3種算法的計算復雜度隨接收通道個數m的變化如圖16所示。

可見，當接收信號通道數目較小時，盲提取算法的運算量略高于盲分離算法。但隨著場景的復雜化，信源數目增多，接收信號通道數目增加，盲分離算法的運算量迅速上升并超過了盲提取算法。這表明，盲提取算法在多信源多通道時相較于盲分離需要的計算量更少，即更適用于復雜電磁環境。

4 結 論

針對戰爭中雷達面臨著主瓣干擾的威脅，本文基于盲信號提取的基本理論，結合陣列天線接收模型以及雷達回波在距離域上與干擾的差異構造最大化信干噪比的目標函數，采用粒子群優化算法進行求解，從混合接收信號中提取出目標回波信號，對主瓣干擾起到了抑制效果。相較于傳統盲分離干擾抑制方法，本文所提的盲提取干擾抑制方法效果優異，能夠應用于欠定場景，受輸入信噪比影響更低;且無需進行信源數目估計，具有更低的運算復雜度以及更廣的適用范圍。

參考文獻

［1］ CARDOSO J F， SOULOUMIAC A. Blind beamforming for non-Gaussian signals［J］. IEE Proceedings F （Radar and Signal Processing）， 1993， 140（6）： 362-370.

［2］ BINGHAM E， HYVARINEN A. A fast fixed-point algorithm for independent component analysis of complex valued signals［J］." International Journal of Neural Systems， 2000， 10（1）： 1-8.

［3］ GE M M， CUI G L， YU X X， et al. Main lobe jamming suppression via blind source separation sparse signal recovery with subarray configuration［J］. IET Radar， Sonar amp; Navigation， 2020， 14（3）： 431-438.

［4］ GAO S， YANG X P， LAN T， et al. Radar main-lobe jamming suppression and identification based on robust whitening blind source separation and convolutional neural networks［J］. IET Radar， Sonar amp; Navigation， 2022， 16（3）： 552-563.

［5］ GE M M， CUI G L， YU X X， et al. Mainlobe jamming suppression with polarimetric multi-channel radar via independent component analysis［J］. Digital Signal Processing， 2020， 106： 102806.

［6］ ZHOU B L， LI R F， LIU W J， et al. A BSS-based space-time multi-channel algorithm for complex-jamming suppression［J］. Digital Signal Processing， 2019， 87： 86-103.

［7］ HINDERER S. Blind source separation of radar signals in time domain using deep learning［C］∥Proc.of the IEEE 23rd International Radar Symposium， 2022： 486-491.

［8］ 趙英健， 田波， 王春陽， 等. 基于FDA-MIMO雷達的主瓣SMSP干擾空時域聯合抑制方法［J］. 系統工程與電子技術， 2022， 44（7）： 2157-2165.

ZHAO Y J， TIAN B， WANG C Y， et al. Space-time joint suppression method of main-beam SMSP jamming based on FDA-MIMO radar［J］. Systems Engineering and Electronics， 2022， 44（7）： 2157-2165.

［9］ 高霞， 全英匯， 李亞超， 等. 基于BSS的FDA-MIMO雷達主瓣欺騙式干擾抑制方法［J］. 系統工程與電子技術， 2020， 42（9）： 1927-1934.

GAO X， QUAN Y H， LI Y C， et al. Main-lobe deceptive jamming suppression with FDA-MIMO radar based on BSS［J］. Systems Engineering and Electronics， 2020， 42（9）： 1927-1934.

［10］ 房津輝， 宋寶軍， 朱明哲. 基于改進的盲源分離算法抗主瓣SMSP干擾［J］. 現代雷達， 2023， 45（2）： 8-15.

FANG J H， SONG B J， ZHU M Z. Anti-mainlobe SMSP interfe-rence based on improved blind source separation algorithm［J］. Modern Radar， 2023， 45（2）： 8-15.

［11］ HAN X F， HE H F， ZHANG Q， et al. Main-lobe jamming suppression method for phased array netted radar based on MSNR-BSS［J］. IEEE Sensors Journal， 2022， 22（23）： 22972-22984.

［12］ YAN Z X， GE M M， CUI G L， et al. DOA estimation with subarrays via blind source separation algorithm［C］∥Proc.of the IEEE Radar Conference， 2021.

［13］ 王川川， 汪亞， 王華兵. 時變環境對信源數估計及盲源分離的影響分析［J］. 兵工自動化， 2022， 41（3）： 1-9.

WANG C C， WANG Y， WANG H B. Influence analysis of time-varying environment on source number estimation and blind source separation［J］. Ordnance Industry Automation， 2022， 41（3）： 1-9.

［14］ LU W， RAJAPAKSE J C. ICA with reference［J］. Neurocomputing， 2006， 69（16/18）： 2244-2257.

［15］ HUANG D S， MI J X. A new constrained independent component analysis method［J］. IEEE Trans.on Neural Networks， 2007， 18（5）： 1532-1535.

［16］ LIN Q H， ZHENG Y R， YIN F L， et al. A fast algorithm for one-unit ICA-R［J］. Information Sciences， 2007， 177（5）： 1265-1275.

［17］ LIU W， MANDIC D P， CICHOCKI A. Blind source extraction based on a linear predictor［J］. IET Signal Processing， 2007， 1（1）： 29-34.

［18］ LEONG W Y， MANDIC D P， WEI L. Blind extraction of noisy events using nonlinear predictor［C］∥Proc.of the IEEE Interna-tional Conference on Acoustics， Speech and Signal Processing， 2007： 657-660.

［19］ BARROS A K， CICHOCKI A. Extraction of specific signals with temporal structure［J］. Neural Computation， 2003， 13（9）： 1995-2003.

［20］ FAN K G， HOU H N， TANG Y F， et al. Orthogonality constrained analytic CMA for blind signal extraction improvement［J］. Signal Processing， 2023， 205： 108880.

［21］ MALEK J， JANSKY J， KOUNOVSKY T， et al. Blind extraction of moving audio source in a challenging environment supported by speaker identification via X-vectors［C］∥Proc.of the IEEE International Conference on Acoustics， Speech and Signal Processing， 2021： 226-230.

［22］ OLIVEIRA P M R， GOULART J H M， FERNANDES C A R， et al. Blind source separation in persistent atrial fibrillation electrocardiograms using block-term tensor decomposition with Lowner constraints［J］. IEEE Journal of Biomedical and Health Informatics， 2022， 26（4）： 1538-1548.

［23］ TANG J L， ZHOU J， WU X， et al. Blind extraction of acoustic signals from rolling bearing composite faults based on ISCA-IMCKD［J］. Measurement Science and Technology， 2023， 34（11）： 115124.

［24］ HAN N， MHASKAR H N， CHUI C K. Theory-inspired deep network for instantaneous-frequency extraction and subsignals recovery from discrete blind-source data［J］. IEEE Trans.on Neural Networks and Learning Systems， 2022， 33（8）： 3437-3447.

［25］ MALEK J， CMEJLA J， KOLDOVSKY Z. Blind extraction of target speech source： three ways of guidance exploiting supervised speaker embeddings［C］∥Proc.of the International Workshop on Acoustic Signal Enhancement， 2022.

［26］ LI L， CHUI C K， JIANG Q T. Direct signal separation via extraction of local frequencies with adaptive time-varying parameters［J］. IEEE Trans.on Signal Processing， 2022， 70： 2321-2333.

［27］ WANG L， ZHAO C H， DONG M X， et al. Fetal ECG signal extraction from long-term abdominal recordings based on adaptive QRS removal and joint blind source separation［J］. IEEE Sensors Journal， 2022， 22（21）： 20718-20729.

［28］ 李廣明， 胡志輝. 基于人工蜂群算法的混沌信號盲提取［J］. 物理學報， 2016， 65（23）： 230501.

LI G M， HU Z H. Blind chaotic signal extraction based on artificial bee colony algorithm［J］. Acta Physica Sinica， 2016， 65（23）：

230501.

［29］ 黃錦旺， 呂善翔， 李廣明， 等. 基于增殖系數的混沌信號提取算法［J］. 電子學報， 2019， 47（4）： 855-861.

HUANG J W， LYU S X， LI G M， et al. Chaotic signal extraction algorithm based on proliferation exponent［J］. Acta Electronica Sinica， 2019， 47（4）： 855-861.

［30］ 趙仕良， 谷婧， 張婕， 等. 任意占空比數字信號位同步時鐘盲提取的數字實現［J］. 電子科技大學學報， 2021， 50（5）： 710-719.

ZHAO S L， GU J， ZHANG J， et al. Digital realization of blind extraction for bit synchronized clock of digital signal with any duty cycle［J］. Journal of University of Electronic Science and Technology of China， 2021， 50（5）： 710-719.

［31］ KUBO Y， TAKAMUNE N， KITAMURA D， et al. Blind speech extraction based on rank-constrained spatial covariance matrix estimation with multivariate generalized Gaussian distribution［J］. IEEE/ACM Trans.on Audio， Speech， and Language Processing， 2020， 28： 1948-1963.

［32］ HUANG G M， YANG L X. Radar signal sorting based on blind signal extraction［C］∥Proc.of the International Confe-rence on Signal Processing， 2004： 2120-2123.

［33］ 饒妮妮， 王祥林， 周博， 等. 線性預測盲源提取算法應用于陣列雷達的分析［J］. 電子科技大學學報， 2010， 39（1）： 1-5.

RAO N N， WANG X L， ZHOU B， et al. Application analysis of blind source extraction algorithm in array radar based on li-near prediction［J］. Journal of University of Electronic Science and Technology of China， 2010， 39（1）： 1-5.

［34］ WANG X L， RAO N， CHENG Y F， et al. An effective BSE-ST method for radar target detection in inhomogeneous clutter/interference environments［C］∥Proc.of the 9th International Conference on Signal Processing， 2008： 2322-2325.

作者簡介

于 雷（1981—），男，副教授，博士，主要研究方向為雷達信號處理、抗干擾抗雜波、波形設計。

劉一品（2001—），男，博士研究生，主要研究方向為雷達干擾抑制、盲信號分離。

位寅生（1974—），男，教授，博士，主要研究方向為對海新體制雷達系統探測技術、雷達抗干擾。