多星姿態協同中的幾何魯棒控制

摘 要：

針對多星系統的姿態協同控制問題，通過不變擴展卡爾曼濾波（invariant extended Kalman filter， InEKF）對航天器進行姿態估計，將航天器的姿態估計與傳遞矩陣獨立;結合無向通信拓撲構建多星特殊正交群（special orthogonal group， SO（3））姿態模型，推導SO（3）上姿態協同誤差。然后，基于SO（3）提出基于一致性理論的姿態協同控制算法。其中，利用徑向基函數神經網絡對虛擬擾動進行擬合補償，所提出的算法考慮空間擾動，以保證協同控制器適用于整個姿態空間，實現多星姿態協同、跟蹤期望姿態和執行器能力約束下的協同。根據LaSalle不變集理論對系統進行分析，證明系統具有全局漸近穩定性。最后，利用六星航天器系統校驗了所提姿態協同控制算法的有效性。

關鍵詞：

多航天器; 特殊正交群; 協同控制; 徑向基函數; 不變擴展卡爾曼濾波

中圖分類號：

V 448.2

文獻標志碼： A""" DOI：10.12305/j.issn.1001-506X.2024.09.24

Geometrically robust control in multi-satellite attitude coordination

HU Yang1， LIU Xuechao2， LI Huayi1，*， CAO Qian1

（1. School of Astronautics， Harbin Institute of Technology， Harbin 150001， China;

2. DongFangHong Satellite Company Limited， Beijing 100094， China）

Abstract：

Aiming at the attitude cooperative control problem of multi-spacecraft system， the attitude estimation of the spacecraft is estimated by invariant extended Kalman filter （InEKF）， and the attitude estimation of the spacecraft is made independent of the transfer matrix. Then， the multi-spacecraft special orthogonal group （SO（3）） attitude model is constructed by combining the undirected communication topology，

and the attitude coordination error on SO（3） is deduced. Among them， an attitude coordination control algorithm based on the consistency theory is proposed based on the special orthogonal group SO（3）. The radial basis function neural network is used to fit and compensate virtual disturbances. The proposed algorithm considers spatial disturbances to ensure that the collaborative controller is applicable to the entire attitude space. Multi-satellite attitude collaboration， tracking desired attitude， and" collaboration under the constraints of actuator capabilities are realized. The system is analyzed based on LaSalle invariant set theory， proving that the system has global asymptotic stability. Finally， the effectiveness of the proposed attitude collaborative control algorithm is verified by using a six-satellite spacecraft system.

Keywords：

multiple spacecraft; special orthogonal group （SO（3））; coordinated control; radial basis function （RBF）; invariant extended Kalman filter （InEKF）

0 引 言

多星系統由多個航天器組成，通過系統的信息交互和共同工作實現，有著傳統獨立航天器不可比擬的優勢，包括結構靈活、研制費用低、安全性高、生命周期長、綜合效率高、發射風險低等優點。姿態協同［1］表示利用所設計的協同控制律，對系統內成員之間的相對姿態和角速度進行調整，使各成員航天器姿態穩定在要求的姿態上，完成相應的任務要求。在航天器控制領域，姿態協同控制有良好的實際應用前景［2］和富有啟發性的理論研究意義［3］。

描述多星協同控制時，多星的系統模型由各成員衛星的姿態信息和系統的通信拓撲構成［4］，結合多星系統的通信拓撲，利用與自身通信的航天器的狀態信息設計控制律，采用分布式的控制思想［5］。基于該情況，文獻［6］研究多個歐拉-拉格朗日系統的一致性問題，解決具有互連時變延遲且不使用速度測量的無領導者和領導者-追隨者一致性問題。航天器的姿態控制具有挑戰性的原因之一在于姿態在非線性流形特殊正交群（special orthogonal group， SO（3））上的演變［7］，在現有的大部分文獻中，姿態通常采用四元數模型、修正羅格里德參數（modified Rodrigues parameters， MRPs）［8-9］和歐拉角式［10］來描述。以上3種姿態描述方式均存在有一定的局限性［11］：四元數模型可以有效地描述旋轉和方向［12］，避免了角度奇異問題，但其引入了模糊性，由于同一個姿態可以由兩個相反四元數表示，導致不期望的“卷繞”現象。歐拉角通過在局部表征姿態來解決此類問題。但不可避免地在控制器設計中引入奇異性，因此并非全局有效［13］，不能使用基于歐拉角的控制方法進行大角度機動。MRPs模型有奇異性的特點，同時是一種非全局描述。綜合所有的姿態描述方式，文獻［14］利用SO（3）描述剛體的姿態并設計控制律。文獻［15-16］研究剛體姿態動力學的跟蹤控制系統，選取姿態誤差函數，獲得理想的姿態跟蹤性能。SO（3）誤差有不同的描述方法［17］，因此基于SO（3）的多星系統控制指令和控制目標［18］需要重新推導。此外，已經提出的SO（3）控制器多數是線性的［19-20］，對于非線性適用與應用較難［21］。在姿態估計的問題上，傳統的擴展卡爾曼濾波（extended Kalman filter， EKF）在處理線性高斯系統時具有巨大的優勢［22］。本文基于矩陣李群進行姿態估計，不變EKF（invariant EKF， InEKF）更有優勢，其傳遞矩陣的計算不依賴于系統的估計值，保證了濾波器的穩定性［23］。同時，基于InEKF的姿態估計不再受限于小角度假設的限制。

對于多智能體系統一致性問題的研究，Olfati-Saber［24］利用圖論和矩陣理論知識對線性化的Vicsek模型一致性現象進行較完整的證明。目前，研究者提出了多種協同控制結構，其中包括傳統的環式結構、虛擬式結構、領航跟隨式結構以及基于行為式的結構，此外還有流行的分布式結構。文獻［25］針對具有弱通訊的高階嚴反饋非線性多智能體系統，提出一種分布式自適應反演控制方法，并研究該系統的協同跟蹤控制問題。基于一致性算法的協同控制優勢顯著，包括所需信息量少、抗干擾能力強、可靠性高、算法可重構性強等特點，然而先前文獻設計的協同控制律的姿態描述建立在四元數或者修正羅德里格參數，適用范圍存在局限。另外，李群的性質也導致姿態模型不能直接利用SO（3）導出。

針對其他姿態描述方式的不足，本文的多星系統基于李群上的SO（3），設計基于該姿態描述的協同控制律，改進一種采用旋轉矩陣形式的協同姿態確定方法。基于一致性理論和SO（3）姿態模型，設計多星姿態協同控制律，并考慮了給定期望姿態和執行器能力約束的情況。利用徑向基函數（radial basis function， RBF）神經網絡對多星系統的空間虛擬擾動進行擬合，使動力學模型更接近空間實際。文中針對包含六顆衛星的航天器系統對設計的控制律進行分析，理論分析與實驗結果相符，驗證了采用SO（3）姿態描述的協同控制律能夠實現航天器系統穩定的姿態協同。

1 多星姿態協同系統建模

1.1 航天器通信拓撲描述

圖論中圖的方向性可以直觀地展現航天器系統中的信息交互。為了使模型更加清晰，將圖論的基本概念運用到多星系統中［26］。在一個無向圖中，圖中的每一個頂點對應多星系統中成員航天器，航天器間的信息交互與通信則利用圖的邊描述。

針對文中提出的控制律，不考慮信息交互的方向。多星系統的通信拓撲利用無向圖進行表述，設有一個邊集E={e1，e2，…，en}和一個頂點集V={v1，v2，…，vn}，如果在E中的任一條邊ek，V中都有一個頂點對（vi，vj）與其對應，那么由V和E組成的集體便稱為一個圖，記為G=（V，E）。與當前頂點存在通信的頂點集合記為Θ，d（v）表示頂點v的度。

4 仿真校驗

在本節中，將定理1和說明1、2應用于6個航天器的姿態協同仿真。航天器的初始姿態、角速度和質量特性參數如表1所示。

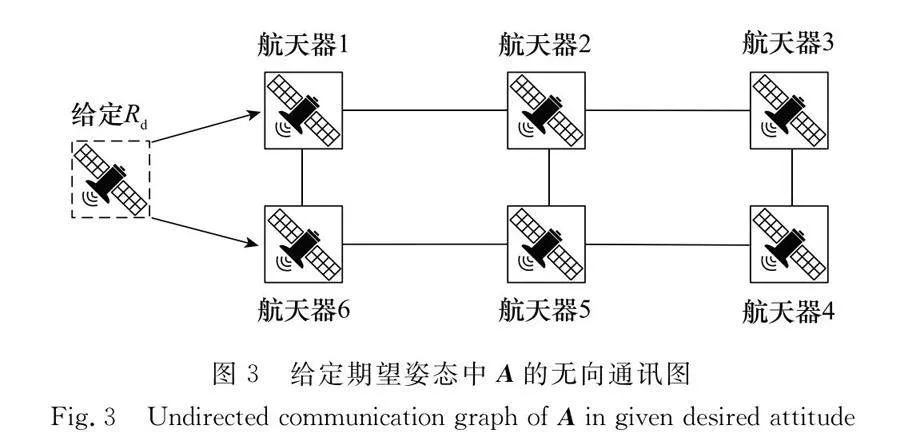
簡單起見，設A=B，A由aij定義，表示姿態參量的鄰接矩陣，B由bij定義，表示角速度的鄰接矩陣。仿真中，A的無向通信圖分別如圖2和圖3所示。i和j之間的一條邊表示第i和j個航天器可以相互通信，對于提出的控制律，若（i，j）∈ε，則有aij=bij=1（i，j=1，2，…，6），否則aij=bij=0。

在RBF神經網絡對空間擾動的估計中，選取的RBF神經網絡結構為1-100-1，其中c=（1∶1∶100），qj=0.5，神經網絡隱含層節點為100個;航天器運行高度取在600 km圓軌道。姿態估計時初始協方差矩陣取I3，噪聲選取高斯噪聲。

在仿真圖中，通過圖例區分不同的航天器。下標j表示航天器在j方向上的分量（j=x，y，z），Tx表示航天器在X方向上的控制力矩。以下，為了簡單起見，選擇航天器1、3、5來展示仿真結果。

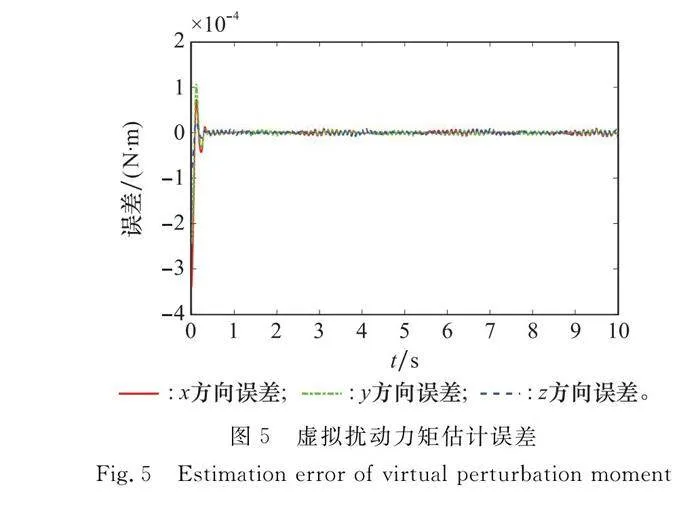
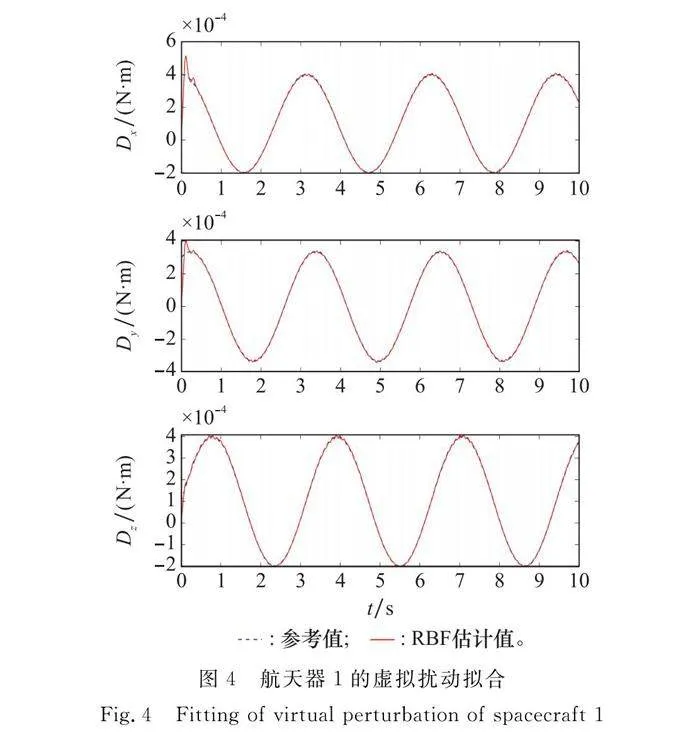
圖4展示了利用RBF神經網絡擬合航天器1所受到的空間虛擬擾動。圖5展示了航天器1空間虛擬擾動力矩估計的誤差曲線，3個方向的擾動估計誤差最后穩定在10－5 N·m附近，RBF神經網絡對虛擬擾動力矩的擬合效果良好。

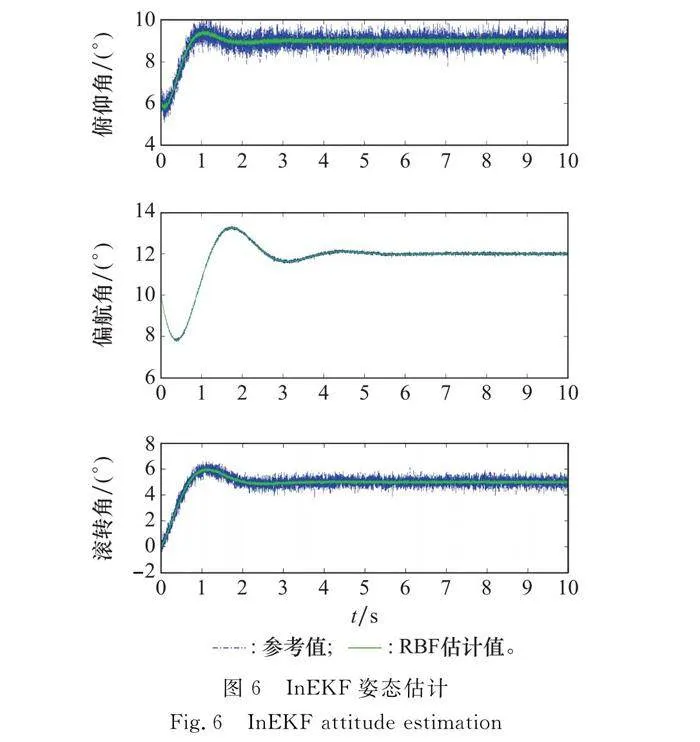
文中以航天器1為例在圖6展示在式（47）控制律下InEKF姿態估計前后姿態的變化。InEKF姿態估計較好地完成了對航天器的姿態估計。

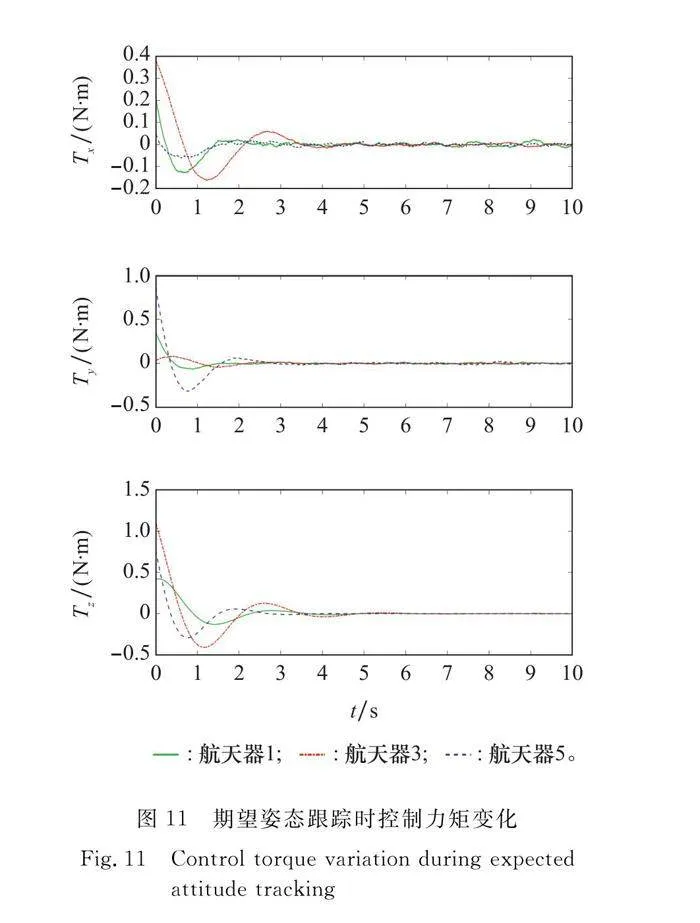
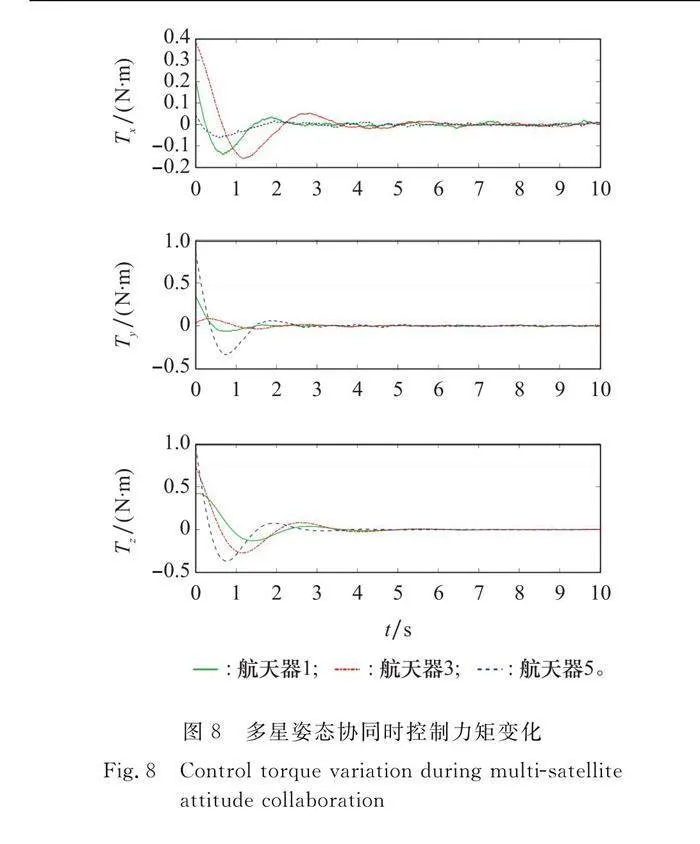
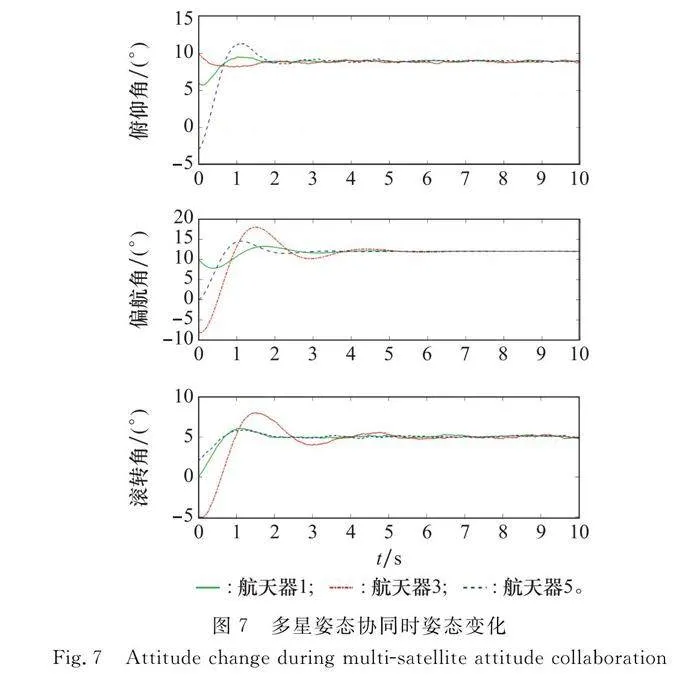
航天器姿態在控制器設計和仿真中使用R，為了清晰地展示仿真結果，本文將R轉換為姿態角度。圖7顯示了航天器1、3、5的姿態在式（42）控制律下的變化，其中p=3，d=1。而圖8顯示了航天器1、3、5的控制力矩在式（42）控制律下的變化。通過圖像，可以看出本文使用SO（3）的控制律很快地收斂，但是在姿態協同的過程中，控制力矩不平滑，這主要是引入了姿態估計的原因。注意到，每個航天器在將近6 s時以相同的姿態和相同的角速度實現姿態協同。

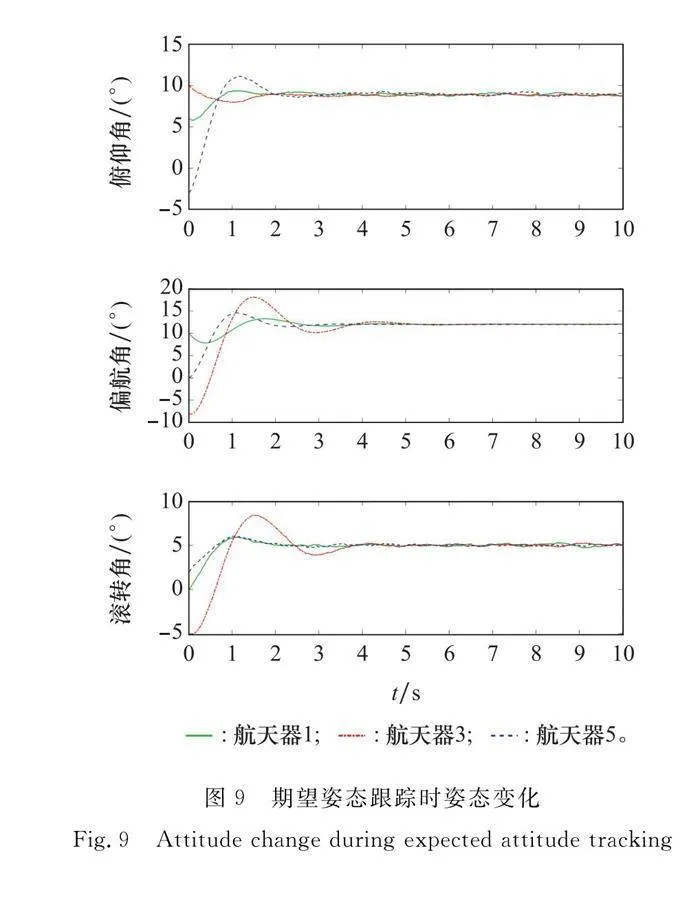
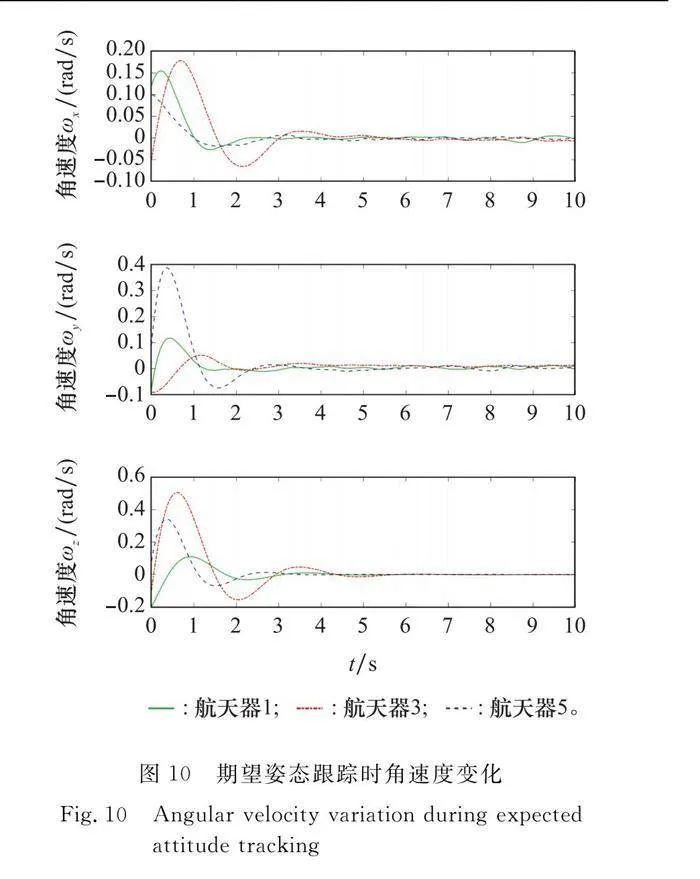
圖9～圖11分別顯示了航天器1、3、5在式（47）控制律下的姿態、角速度和控制力矩變化。其中，p=10，d=6。注意到，每個航天器都達到相同的姿態，并在將近8 s時指向所需的恒定參考姿態，其中給定的參考姿態為俯仰角9°、偏航角12°、滾轉角5°。同時，航天器的角速度最終收斂于零。

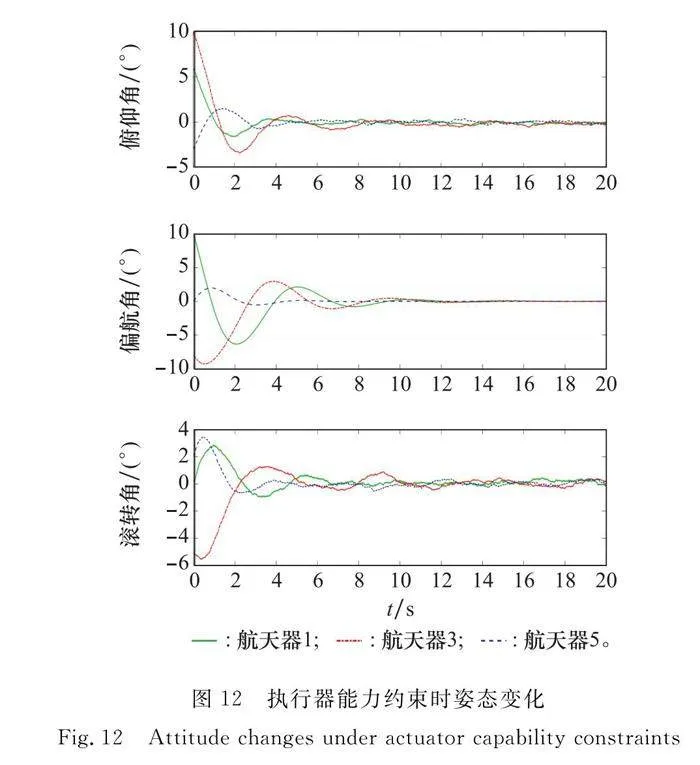
圖12和圖13分別顯示了航天器1、3、5考慮執行器能力約束時的姿態、控制力矩變化。其中，p=10，d=5。注意到，每個航天器的控制力矩有所減小，但與此同時，控制時長有所增加，在將近16 s時指向參考姿態。

為了更加準確地描述多星系統成員航天器之間姿態協同過程的整體精準度，引入姿態相對誤差量Eco來反映系統姿態協同的效果［4］。Eco的計算方式如下：

Eco=15∑5i=1errori（55）

式中：errori=ri－r6，ri=［i，θi，i］T，i，θi和i分別表示成員衛星姿態的偏航、俯仰、滾轉;Eco為姿態相對誤差量，表示系統中其他航天器與選定航天器的平均姿態誤差。為了說明本文所提控制器的優勢，文中設置與表1相同的仿真初始狀態，如圖14所示。

圖14中，文獻［3］是利用四元數姿態描述的協同控制方法;文獻［4］則是基于SO（3）模型提出的反步滑模控制器用于多星姿態協同。

從圖14得知，相對姿態誤差Eco逐漸收斂為0，表明系統實現了姿態協同。與其他兩種方法的對比，驗證了所設計的控制器的有效性和快速性。

5 結 論

本文針對SO（3）上多個航天器之間的姿態協同問題，在無向通信拓撲圖下提出了姿態協同控制律，考慮給定期望姿態和執行器能力約束的情況。利用InEKF多星系統進行了姿態估計，將航天器的姿態估計與傳遞矩陣獨立，姿態參數的更新依賴于誤差η;利用RBF神經網絡對虛擬擾動進行擬合，并在控制器中實現了擾動補償，使其具有良好的魯棒性。仿真結果表明，利用InEKF進行姿態估計和RBF神經網絡進行擾動補償的控制律具有較好的控制效果。

參考文獻

［1］ FAN L M， HUANG H， ZHOU K X. Robust fault-tolerant attitude control for satellite with multiple uncertainties and actuator faults［J］. Chinese Journal of Aeronautics， 2020， 33（12）： 3380-3394.

［2］ CAPUANO V， HARVARD A， CHUNG S J. On-board cooperative spacecraft relative navigation fusing GNSS WITH vision［J］. Progress in Aerospace Sciences， 2022， 128： 100761.

［3］ YE D， ZOU A M， SUN Z W. Predefined-time predefined-bounded attitude tracking control for rigid spacecraft［J］. IEEE Trans.on Aerospace Electronic Systems， 2022， 58（1）： 464-472.

［4］ 馬鳴宇， 董朝陽， 馬思遷， 等. 多航天器反步滑模SO（3）協同控制［J］. 宇航學報， 2018， 39（6）： 664-673.

MA M Y， DONG C Y， MA S Q， et al. Coordinated attitude CONTROL of multiple spacecraft via backstepping sliding mode method on SO（3）［J］. Journal of Astronautics， 2018， 39（6）： 664-673.

［5］ WANG W T， XIANG Z R. Distributed consensus tracking control for nonlinear multiagent systems with state delays and unknown control coefficients［J］. International Journal of Robust and Nonlinear Control， 2021， 32（4）： 2050-2068.

［6］ NUNO E， ORTEGA R. Achieving consensus of Euler-Lagrange agents with interconnecting delays and without velocity measurements via passivity-based control［J］. IEEE Trans.on Control Systems Technology， 2018， 26（1）： 222-232.

［7］ GAO H， XIA Y Q， ZHANG X P， et al. Distributed fixed-time attitude coordinated control for multiple spacecraft with actuator saturation［J］. Chinese Journal of Aeronautics， 2022， 35（4）： 292-302.

［8］ REN Y， WANG H M， XIE D， et al. New terminal sliding mode consensus algorithm for disturbed second-order multi-agent systems［J］. International Journal of Control， Automation， and Systems， 2022， 20（8）： 2534-2542.

［9］ LIANG S， WANG F Y， LIU Z X， et al. Necessary and sufficient conditions for leader-follower consensus of discrete-time multiagent systems with smart leader［J］. IEEE Trans.on Systems， Man， and Cybernetics： Systems， 2021， 52（5）： 2779-2788.

［10］ DU H B， ZHU W W， WEN G H， et al. Finite-time formation control for a group of quadrotor aircraft［J］. Aerospace Science and Technology， 2017， 69： 609-616.

［11］ XIE X， SHENG T， HE L， et al. Distributed attitude consensus tracking control for spacecraft formation flying via adaptive nonsingular fast terminal sliding mode control［J］. Journal of Aerospace Engineering， 2022， 236（8）： 1603-1616.

［12］ YEFYMENKO N， KUDERMETOV R. Quaternion models of a rigid body rotation motion and their application for spacecraft attitude control［J］. Acta Astronautica， 2022， 194： 76-82.

［13］ ZHANG L， LIU Q Z， FAN G W， et al. Parametric control for flexible spacecraft attitude maneuver based on disturbance observer［J］. Aerospace Science and Technology， 2022， 130： 107952.

［14］ CHATURVEDI N A. Global dynamics and stabilization of rigid body attitude systems［D］. Ann Arbor： University of Michigan， 2007.

［15］ POSIELEK T， JOHANN R. Attitude reconstruction of a spacecraft from temperature measurements in solar eclipse analysis and observer design for a not globally observable nonlinear system［J］. IEEE Trans.on Control Systems Technology， 2023， 31（2）： 631-645.

［16］ HU D Y， ZHAO X T， ZHANG S J. Robust image-based coordinated control for spacecraft formation flying［J］. Chinese Journal of Aeronautics， 2022， 35（9）： 268-281.

［17］ HASHEMI S H， PARIZ N， HOSSEINI S S K. Observer-based hybrid control for global attitude tracking on SO（3） with input quantisation［J］. International Journal of Control， 2022， 96（5）： 1352-1363.

［18］ MENG Q K， YANG H， JIANG B. Second-order sliding-mode on SO（3） and fault-tolerant spacecraft attitude control［J］. Automatica， 2023， 149： 110814.

［19］ SHI Z， XIE Y E， DENG C C， et al. Disturbance observer based finite-time coordinated attitude tracking control for spacecraft on SO（3）［J］. Journal of Systems Engineering and Electronics， 2020， 31（6）： 1274-1285.

［20］ ZHEN Q Z， WAN L， LI Y L， et al. Formation control of a multi-AUVs system based on virtual structure and artificial potential field on SE（3）［J］. Ocean Engineering， 2022， 253： 111148.

［21］ LEE T. Global exponential attitude tracking controls on SO（3）［J］. IEEE Trans.on Automatic Control， 2015， 60（10）： 2837-2842.

［22］ 邵海俊， 繆玲娟， 郭巖冰. 一種用于SINS行進間對準的模糊抗野值濾波算法［J］. 宇航學報， 2020， 41（4）： 447-455.

SHAO H J， MIAO L J， GUO Y B. A robust filter based on fuzzy theory for SINS in-motion alignment［J］. Journal of Astronautics， 2020， 41（4）： 447-455.

［23］ BARRAU A， BONNABEL S. Invariant Kalman filtering［J］. Annual Review of Control Robotics and Autonomous Systems， 2018， 1（1）： 237-257.

［24］ OLFATI-SABER R. Flocking for multi-agent dynamic systems： algorithms and theory［J］. IEEE Trans.on Automatic Control， 2006， 51（3）： 401-420.

［25］ 周健， 龔春林， 粟華， 等. 復雜約束下的編隊姿態有限時間協同控制方法［J］. 宇航學報， 2018， 39（12）： 1340-1347.

ZHOU J， GONG C L， SU H， et al. Finite-time distributed synchronization of spacecraft formation attitude with complex constraints［J］. Journal of Astronautics， 2018， 39（12）： 1340-1347.

［26］ ELAHI A， ALFI A， MODARES H. Distributed consensus control of vehicular platooning under delay， packet DROPOUT and noise： relative state and relative input-output control strategies［J］. Transactions on Intelligent Transportation Systems， 2022， 23（11）： 20123-20133.

［27］ HUO J H， MENG T， JIN Z H. Adaptive attitude control using neural network observer disturbance compensation technique［C］∥Proc.of the IEEE 9th International Conference on Recent Advances in Space Technologies， 2019： 697-701.

［28］ WANG Z， WU Z. Nonlinear attitude control scheme with disturbance observer for flexible spacecrafts［J］. Nonlinear Dynamics， 2015， 81（1/2）： 257-264.

［29］ YAN R D， WU Z. Nonlinear disturbance observer-based spacecraft attitude control subject to disturbances and actuator faults［C］∥Proc.of the 5th International Conference on Computer-Aided Design， Manufacturing， Modeling and Simulation， 2017.

［30］ LEE D. Nonlinear disturbance observer-based robust control for spacecraft formation flying［J］. Aerospace Science and Technology， 2018， 76： 82-90.

［31］ ALIPOUR M， FANI S F， KABGANIAN M. Inertia-free nonlinear attitude tracking with disturbance compensation using adaptive-sliding control based on quaternion algebra［J］. Simulation， 2020， 96（1）： 43-54.

［32］ AMIRKHANI A， BARSHOOI A H. Consensus in multi-agent systems： a review［J］. Artificial Intelligence Review， 2022， 55（5）： 3897-3935.

作者簡介

胡 洋（1999—），男，碩士研究生，主要研究方向為航天器協同控制與接管控制。

劉學超（1980—），男，高級工程師，主要研究方向為飛行器總體設計。

李化義（1978—），男，教授，博士，主要研究方向為動力學與控制、空間遙感。

曹 芊（1997—），男，博士研究生，主要研究方向為動力學與控制。