“基于思想方法”視角下的高中數(shù)學(xué)教學(xué)探究

數(shù)學(xué)思想方法是數(shù)學(xué)學(xué)習(xí)的核心價值，是數(shù)學(xué)知識體系架構(gòu)的靈魂，它如同引領(lǐng)學(xué)生深入數(shù)學(xué)學(xué)習(xí)的鑰匙，能夠幫助學(xué)生打開理解數(shù)學(xué)概念、公式、定理等基礎(chǔ)知識的大門，既能強(qiáng)化學(xué)生對概念、公式、定理等數(shù)學(xué)基礎(chǔ)知識的理解，又能鍛煉學(xué)生的邏輯和抽象思維，為學(xué)生更高緯度的數(shù)學(xué)學(xué)習(xí)打下基礎(chǔ)。數(shù)學(xué)思想方法蘊(yùn)含在數(shù)學(xué)知識的傳授中，具有潛移默化影響的特點，所以教師在規(guī)劃課堂教學(xué)活動時，要深入鉆研教材，善于通過對教材和課標(biāo)的研究，總結(jié)歸納出知識中蘊(yùn)含的基本思想方法，在此基礎(chǔ)上，精心地設(shè)計教學(xué)過程，在知識講授的同時滲透思想方法，提升學(xué)生的數(shù)學(xué)素養(yǎng)。

1.基本思想方法

數(shù)學(xué)基本思想源自史寧中撰寫的《數(shù)學(xué)思想方法概論》，先后通過義務(wù)教育和高中課程標(biāo)準(zhǔn)呈現(xiàn)。史寧中第一次明確了數(shù)學(xué)基本思想的判斷標(biāo)準(zhǔn)，這些思想首先是數(shù)學(xué)產(chǎn)生和發(fā)展所必須依賴的，其次是通過對數(shù)學(xué)的學(xué)習(xí)應(yīng)該具備的基本思維方式。數(shù)學(xué)方法是數(shù)學(xué)思想在實踐中的直接體現(xiàn)，它將抽象的數(shù)學(xué)思想轉(zhuǎn)化為具體、可操作的步驟和程序。數(shù)學(xué)思想蘊(yùn)含在數(shù)學(xué)知識學(xué)習(xí)中，是指向數(shù)學(xué)思維活動內(nèi)部的，是本質(zhì)性的；數(shù)學(xué)方法體現(xiàn)在數(shù)學(xué)解題過程中，是外顯的、具體的，指向數(shù)學(xué)思維活動的外部，具有可操作性。數(shù)學(xué)基本思想的核心要素（如抽象、推理、模型等）蘊(yùn)含在數(shù)學(xué)思想方法中，是抽象、概括更高層次的數(shù)學(xué)思想方法而形成的更深刻的觀點。

數(shù)學(xué)思想方法是以數(shù)學(xué)知識和技能為基礎(chǔ)，以數(shù)學(xué)思想為內(nèi)涵，以數(shù)學(xué)方法為外延，緊密聯(lián)系數(shù)學(xué)教育教學(xué)和數(shù)學(xué)學(xué)習(xí)過程，指向數(shù)學(xué)活動經(jīng)驗的積累和思維習(xí)慣的形成，二者的交融和統(tǒng)一即數(shù)學(xué)思想方法。

2.“基本思想方法”視角下的高中數(shù)學(xué)教學(xué)實施

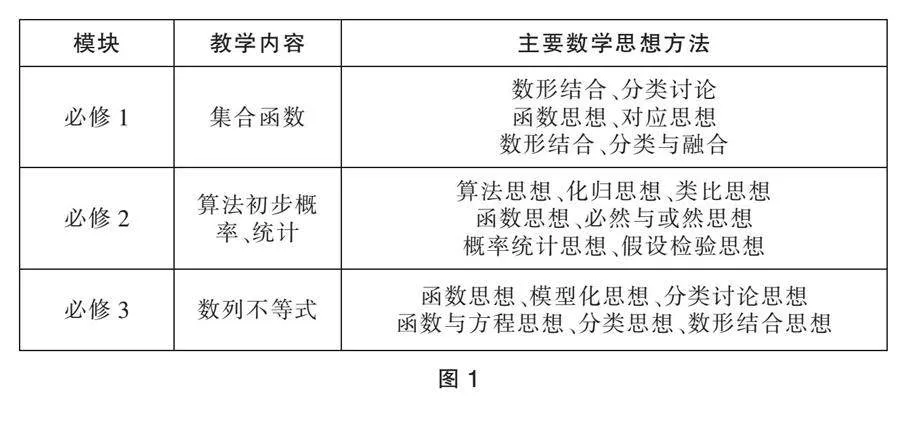
數(shù)學(xué)思想方法與知識內(nèi)容相輔相成，共同構(gòu)成了數(shù)學(xué)課程的核心，在高中數(shù)學(xué)教學(xué)中要將知識教學(xué)與思想方法的培養(yǎng)緊密結(jié)合，形成一個有機(jī)整體。在新的背景下，教師要深入研究新教材、新課標(biāo)，做到對教材每個知識點都有深入的理解和把握，同時深入探究知識點中蘊(yùn)含的思想方法，課堂教學(xué)中，在對知識講解的同時，更注重對學(xué)生思維的培養(yǎng)和啟迪，讓知識的傳授過程和思想方法的領(lǐng)悟過程有機(jī)融合。比如必修1集合和函數(shù)、必修3算法初步和概率統(tǒng)計、必修5數(shù)列和不等式，我們可以梳理和歸納如圖1。

挖掘高中數(shù)學(xué)知識中的思想方法是教學(xué)中滲透思想方法的前提，只有充分地研究教材、研究課標(biāo)，才能析出高中數(shù)學(xué)知識中的思想方法，合理設(shè)計教學(xué)，在知識的傳授中滲透數(shù)學(xué)基本思想方法，潛移默化地影響學(xué)生，下面以不等式知識為例，探究分析不等式中的數(shù)學(xué)思想方法。

人教版新教材不等式放在了高一必修1第二章，不等式安排在高一年級，銜接起初高中知識，起著承上又啟下的作用。不等式知識中包含著高中數(shù)學(xué)中很多重要的思想方法，例如數(shù)形結(jié)合、函數(shù)與方程、分類討論、化歸等。教師在不等式教學(xué)中應(yīng)注重基礎(chǔ)知識與思想方法的有機(jī)結(jié)合，通過個性化教學(xué)、深度挖掘、歸納總結(jié)和實踐應(yīng)用等策略，讓不等式的知識架構(gòu)豐盈起來，讓知識和思想同步領(lǐng)悟，為學(xué)生的數(shù)學(xué)素養(yǎng)和思維能力的提升奠定堅實的基礎(chǔ)。

2.1數(shù)形結(jié)合思想

數(shù)與形作為探究同一數(shù)學(xué)問題的雙重視角，非但不相斥，反而相輔相成，構(gòu)成了彼此轉(zhuǎn)化的橋梁與通道。在解決數(shù)學(xué)難題時，數(shù)形結(jié)合的思想方法尤為關(guān)鍵，它主要分為兩大策略：“以形助數(shù)”與“數(shù)轉(zhuǎn)形現(xiàn)”。

“以形助數(shù)”就是利用圖形的直觀性來理解和解決數(shù)學(xué)問題，這一過程要求我們將圖形的特性、屬性轉(zhuǎn)化為代數(shù)語言，換而言之就是我們利用代數(shù)式、方程或不等式等代數(shù)形式表達(dá)圖形的特征，方便我們依據(jù)數(shù)學(xué)定理、公式進(jìn)行邏輯推理與求解，使得復(fù)雜的數(shù)量問題形象化、可視化，而“數(shù)轉(zhuǎn)形現(xiàn)”則是一種逆向的思考，它將原本抽象、不太容易直接理解的代數(shù)問題，轉(zhuǎn)化為比較直觀形象的幾何圖形問題。數(shù)形結(jié)合的思想方法串聯(lián)起了數(shù)學(xué)中的幾何和代數(shù)，搭建起了數(shù)與形之間的橋梁，數(shù)形結(jié)合思想是數(shù)學(xué)中數(shù)形和諧統(tǒng)一的完美體現(xiàn)，更是一種高效的解題工具與策略。不等式中有著很多數(shù)形結(jié)合思想的應(yīng)用，在日常的課堂教學(xué)中，利用不等式的知識滲透數(shù)形結(jié)合思想方法，在加深學(xué)生對知識的理解的同時，也讓學(xué)生受到了數(shù)學(xué)之美的熏陶。

（一）基本不等式

在基本不等式章節(jié)學(xué)習(xí)中，利用了數(shù)形結(jié)合的幾何方法理解基本不等式。

如圖2，AB是圓的直徑，點C是 AB上一點， AC=a，BC=b。過點C作垂直于AB的弦DE，連接 AD，BD。你能利用這個圖形得出不等式 ≤的幾何解釋嗎？

如圖：

設(shè)半徑為R，則直徑 AB=a+b， R=。

由垂徑定理可知CD= 。

由圖2可知，CD≤R，

故≤

顯然，當(dāng)且僅當(dāng)點C與圓心重合，即a=b時，等號成立。

（二）一元二次不等式及其解法

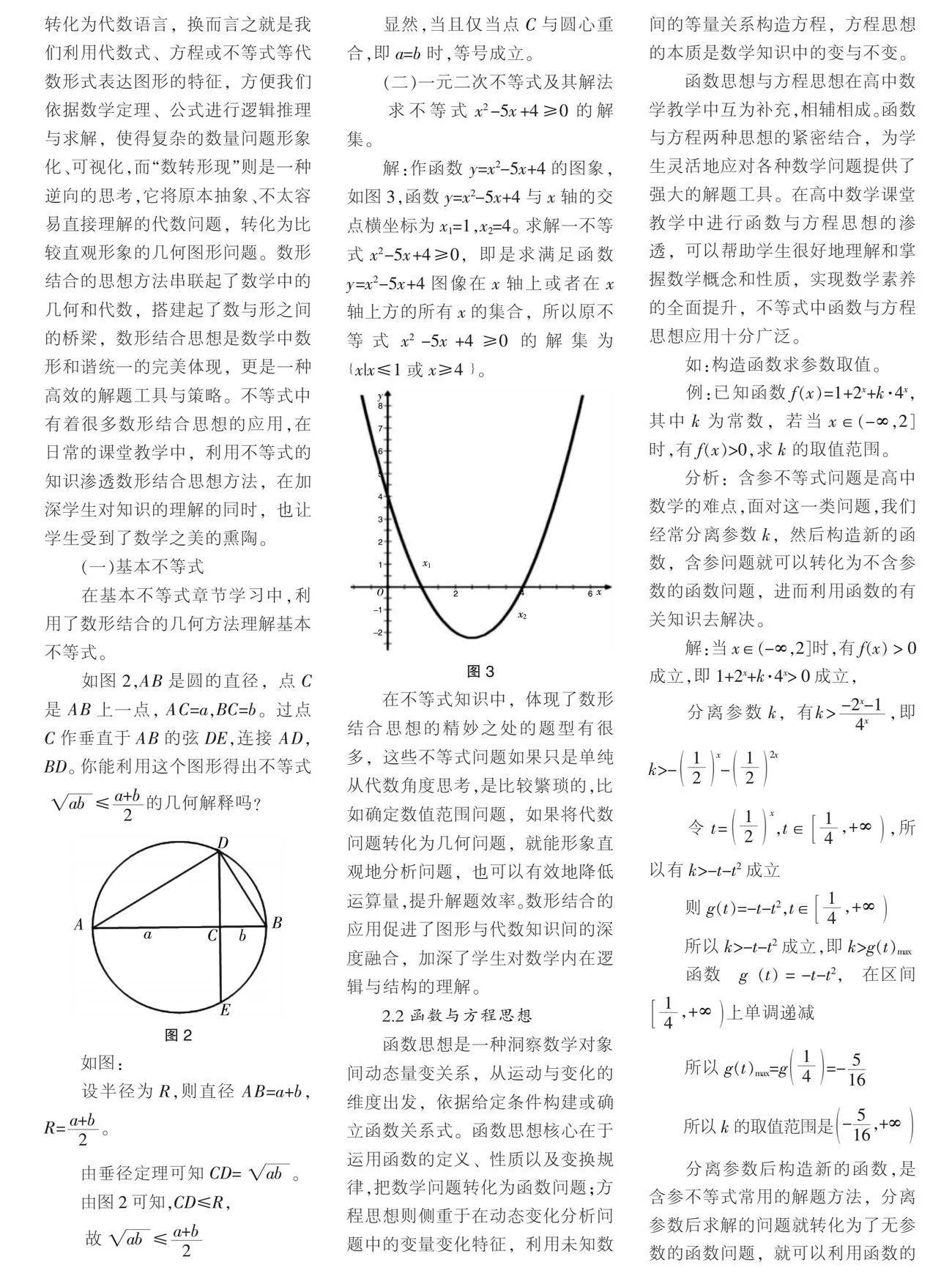
求不等式x2－5x+4≥0的解集。

解：作函數(shù) y=x2－5x+4的圖象，如圖3，函數(shù)y=x2－5x+4與x軸的交點橫坐標(biāo)為x1=1，x2=4。求解一不等式x2－5x+4≥0，即是求滿足函數(shù) y=x2－5x+4圖像在x軸上或者在x軸上方的所有x的集合，所以原不等式x2－5x+4≥0的解集為x｜x≤1或x≥4。

在不等式知識中，體現(xiàn)了數(shù)形結(jié)合思想的精妙之處的題型有很多，這些不等式問題如果只是單純從代數(shù)角度思考，是比較繁瑣的，比如確定數(shù)值范圍問題，如果將代數(shù)問題轉(zhuǎn)化為幾何問題，就能形象直觀地分析問題，也可以有效地降低運(yùn)算量，提升解題效率。數(shù)形結(jié)合的應(yīng)用促進(jìn)了圖形與代數(shù)知識間的深度融合，加深了學(xué)生對數(shù)學(xué)內(nèi)在邏輯與結(jié)構(gòu)的理解。

2.2函數(shù)與方程思想

函數(shù)思想是一種洞察數(shù)學(xué)對象間動態(tài)量變關(guān)系，從運(yùn)動與變化的維度出發(fā)，依據(jù)給定條件構(gòu)建或確立函數(shù)關(guān)系式。函數(shù)思想核心在于運(yùn)用函數(shù)的定義、性質(zhì)以及變換規(guī)律，把數(shù)學(xué)問題轉(zhuǎn)化為函數(shù)問題；方程思想則側(cè)重于在動態(tài)變化分析問題中的變量變化特征，利用未知數(shù)間的等量關(guān)系構(gòu)造方程，方程思想的本質(zhì)是數(shù)學(xué)知識中的變與不變。

函數(shù)思想與方程思想在高中數(shù)學(xué)教學(xué)中互為補(bǔ)充，相輔相成。函數(shù)與方程兩種思想的緊密結(jié)合，為學(xué)生靈活地應(yīng)對各種數(shù)學(xué)問題提供了強(qiáng)大的解題工具。在高中數(shù)學(xué)課堂教學(xué)中進(jìn)行函數(shù)與方程思想的滲透，可以幫助學(xué)生很好地理解和掌握數(shù)學(xué)概念和性質(zhì)，實現(xiàn)數(shù)學(xué)素養(yǎng)的全面提升，不等式中函數(shù)與方程思想應(yīng)用十分廣泛。

如：構(gòu)造函數(shù)求參數(shù)取值。

例：已知函數(shù)f（x）=1+2x+k·4x，其中k為常數(shù)，若當(dāng)x∈（－∞，2］時，有f（x）>0，求k的取值范圍。

分析：含參不等式問題是高中數(shù)學(xué)的難點，面對這一類問題，我們經(jīng)常分離參數(shù)k，然后構(gòu)造新的函數(shù)，含參問題就可以轉(zhuǎn)化為不含參數(shù)的函數(shù)問題，進(jìn)而利用函數(shù)的有關(guān)知識去解決。

解：當(dāng)x∈（－∞，2］時，有f（x） > 0成立，即1+2x+k·4x> 0成立，

分離參數(shù)后構(gòu)造新的函數(shù)，是含參不等式常用的解題方法，分離參數(shù)后求解的問題就轉(zhuǎn)化為了無參數(shù)的函數(shù)問題，就可以利用函數(shù)的有關(guān)性質(zhì)來求解。不等式中涉及多個變量和條件時，我們往往利用方程來建立變量之間的等量關(guān)系，將問題中的未知量轉(zhuǎn)化為已知量，從而讓復(fù)雜的多變量問題變簡單。

函數(shù)與方程思想對學(xué)生深入理解數(shù)學(xué)的本質(zhì)和規(guī)律有著很大的幫助。因此在高中數(shù)學(xué)教學(xué)中，教師應(yīng)該注重課堂教學(xué)設(shè)計，在教學(xué)實施過程中培養(yǎng)學(xué)生的函數(shù)與方程思想意識以及靈活運(yùn)用這些思想解決問題的能力。

2.3分類討論思想

分類討論思想是一種深刻而靈活的數(shù)學(xué)策略，數(shù)學(xué)中有很多錯綜復(fù)雜的難題，這類問題要使用一種系統(tǒng)化、條理化的方法，才能夠思路清晰地解決問題。分類討論思想的核心是根據(jù)問題本身的特性或內(nèi)在規(guī)律，選取合適的分類標(biāo)準(zhǔn)，然后按照分類的標(biāo)準(zhǔn)將復(fù)雜問題拆解為幾個相對簡單、方便處理的問題，最后歸納各部分的結(jié)論，總結(jié)出原問題全面的結(jié)果。

不等式中分類討論思想也隨處可見，例如在求解分式不等式時，會采用化歸的思想，把分式不等式轉(zhuǎn)化為整式不等式，而整式不等式的解決，又要運(yùn)用分類討論的思想，按照分母的正負(fù)性進(jìn)行分類討論；比如在處理含參不等式時，要根據(jù)參數(shù)的不同取值范圍進(jìn)行分類討論，分類討論思想在不等式解題中有著獨特的魅力。

如含參比較大小問題。

比較（a+1）2與a2－2a+3的大小關(guān)系。

分析：作差比較大小，

分類討論思想在不等式知識中的應(yīng)用是一種重要的解題方法，當(dāng)學(xué)生在面對復(fù)雜的不等式問題時，通過不等式的性質(zhì)、結(jié)構(gòu)或條件的不同，把問題分解為幾個相對簡單問題，然后分別進(jìn)行討論解決，最后歸納總結(jié)問題的完整解。分類討論時要做到以下幾點：一是分類應(yīng)逐級進(jìn)行，避免越級跳躍，以確保討論的條理性和邏輯性；二是在同一分類級別內(nèi)，必須采用統(tǒng)一的分類標(biāo)準(zhǔn)，以保持分類的一致性；三是分類時要力求全面，不重不漏。

2.4化歸思想

化歸是轉(zhuǎn)化和歸因的簡稱，化歸是“轉(zhuǎn)化”與“歸因”的緊密結(jié)合，轉(zhuǎn)化是手段，歸因則是目的。化歸是把一個問題從難到易、從繁到簡地轉(zhuǎn)化出來，轉(zhuǎn)化是高中數(shù)學(xué)處理問題的方法和途徑，本質(zhì)上就是尋求問題解題思路與方法，當(dāng)問題比較難或者比較復(fù)雜時我們采取的策略。化歸是實現(xiàn)新舊知識或問題動態(tài)轉(zhuǎn)換的重要數(shù)學(xué)思想方法，也是有效的思想策略和方法，正確的轉(zhuǎn)化是解題成功的關(guān)鍵。化歸思想一般按照以下模式如圖4。

如：求分式不等式解集問題。

求不等式≤0的解集

分析：對于分式不等式≤0，第一種思路是把分式不等式轉(zhuǎn)化為已知的分式知識：同號為正，異號為負(fù)，分母不為零，即轉(zhuǎn)化為f（x）≤0g（x）>0，或者f（x）≥0g（x）<0，另外一種思路是等價轉(zhuǎn)化為f（x）g（x）≤0g（x）≠0，即將分式不等式通過轉(zhuǎn)化等價于整式不等式，而整式不等式也是我們已知掌握的，化未知為已知，化舊知為新知，這就是化歸思想的應(yīng)用，化歸思想求一元二次不等式解集，解決含參不等式問題等中也有體現(xiàn)。

3.總結(jié)

數(shù)學(xué)學(xué)習(xí)顯性的是豐富的知識體系、精確的模型構(gòu)建以及嚴(yán)謹(jǐn)?shù)倪壿嬐评恚[性的是數(shù)學(xué)的基本思想，它們構(gòu)成了數(shù)學(xué)學(xué)科的核心靈魂，對學(xué)生而言，數(shù)學(xué)基本思想方法，是他們深入理解數(shù)學(xué)知識，靈活運(yùn)用數(shù)學(xué)知識解決問題的鑰匙，也是培養(yǎng)他們核心素養(yǎng)、發(fā)展高階思維能力的基石；教師是數(shù)學(xué)思想方法的傳播者和啟迪者，課堂教學(xué)直接影響著學(xué)生對數(shù)學(xué)思想方法的理解和掌握程度，因此教師在規(guī)劃課堂教學(xué)活動時，要深入鉆研教材，善于總結(jié)歸納知識中蘊(yùn)含的基本思想方法；通過對教材和課標(biāo)的研究，靈活設(shè)計課堂教學(xué)過程；在課堂教學(xué)的實施過程中，通過對教材和課標(biāo)的研究，總結(jié)歸納出思想方法并巧妙地融入課堂教學(xué)中，使學(xué)生在領(lǐng)會高中數(shù)學(xué)知識的“體”時又領(lǐng)會了其“魂”，同時又對學(xué)生的數(shù)學(xué)思維能力起到了鍛煉作用，提高學(xué)生的數(shù)學(xué)素養(yǎng)。

責(zé)任編輯 錢昭君