基于改進bi-kmeans算法的學生消費水平分析

摘 要：以高校校園內學生的移動支付消費記錄為基礎數據，利用bi-means聚類算法對其處理并進行分析，挖掘出這些學生消費水平背后的隱藏信息。通過改進歐式距離、k-means和bi-kmeans，應用于清洗過后的消費記錄，劃分出不同層次的學生消費群體，以散點圖的直觀方式呈現。實踐表明，改進后的bi-means算法結果的劃分更合理，可向學校資助部門提供參考。

關鍵詞：bi-kmeans；消費水平；聚類算法；數據挖掘；歐式距離

中圖分類號：TP 312 " " " " 文獻標志碼：A

高校學生采用現代移動支付的方法，在校內的消費行為都會留下詳細記錄。從這些詳細的記錄中分析每個學生的消費水平。本文在傳統bi-kmeans聚類算法和傳統歐式距離的基礎上，提出改進方法，應用于學生消費水平分析，得出結論，并與傳統聚類方法的結論進行比較。

1 研究現狀

1.1 k-means聚類算法

1976年，MacQueen基于前人的研究提出了k-means聚類算法。其中心思想為給定數據集劃分為k個簇，每個簇的質心由全部點的中心來決定。中心是簇中全部點的平均值，稱為k均值，k個初始值由用戶指定。k-means聚類算法的優點為原理簡單、易于實現并且接近線性的時間復雜度。缺點為對k值的設置依賴性較高，還可能限于局部最優。

1.2 bi-kmeans聚類算法

bi-kmeans的基本思想與k-means一致，區別在于k值是從1開始迭代，逐步遞增，直到達到期望值為止。在每次遞增的過程中，選擇可以最大程度地降低平方和誤差SSE的簇，將其一分為二，不斷重復。

因為不需要給定k個初始質心，所以可以避免給定初始質心的不合理性。k值是從1緩慢增長到預期值，在每次迭代的過程中，新的質心和新的簇都是從被分裂簇一分為二產生的。這樣類似細胞一分二的最簡單分裂，不會存在其他分裂方案。

1.3 國內研究

應用范圍最廣的k-means聚類算法已經廣泛適用于數據挖掘任務中。一卡通系統已經在全國高校大范圍推廣，該系統專用于收集高校學生這個特定人群的詳細消費記錄，已經有多人嘗試用k-means結合一卡通的模式進行數據挖掘。龔黎旰等[1]以校園一卡通消費記錄為數據基礎，利用大數據和數據挖掘技術對其進行分析。柴政等[2]利用數據挖掘方法中的神經網絡分析校園一卡通消費記錄，從客觀的角度評判學生的貧困程度及精準地劃分貧困群體。

2 改進算法

bi-kmeans算法來源于k-means算法，而k-means算法又基于歐式距離。傳統的3個算法不能簡單套用，須根據實際環境進行改進。

2.1 改進歐式距離

歐式距離全稱為歐幾里得距離，其中心思想為以向量為基準，衡量多維空間中任意兩點間的絕對距離，即兩點之間的最短直線距離，如公式（1）所示。

（1）

式中：x 、y 為多維空間中的任意兩點；xi和yi分別為兩點各自的各向量； d（x，y）為歐式距離。

當衡量真實的多維空間中的兩點距離時，歐式距離非常有效。當應用于抽象概念的空間中兩點距離時，歐式距離會暴露出一定的弊端。當其中某些向量顯著大于其他向量甚至差距大到數量級差異時，歐式距離的結果不再是由各向量共同決定的。其決定因素只由數量級最大的向量構成，次數量級向量和小數量級向量的影響因子大幅度縮小，幾乎不起作用。

令各向量回歸到同一個數量級別即可避免這個弊端，比較有效且簡潔的解決辦法是縮小較大向量的數量級或增加較小向量的數量級。因為這樣可以從源頭減少整個算法過程的計算量，所以縮小較大向量的數量級更有效，在歐式距離中為各向量增加權重，稱為加權歐式距離，如公式（2）所示。

（2）

式中：wi為各向量的權重，其余標識與公式（1）完全一致。

2.2 改進k-means

k-means也稱為k均值，其是最簡單的聚類算法，具有通俗易懂、易于實現的優點。其工作原理如下。

步驟一：確定k個初始點作為初始質心。這k個初始質心不必要求為數據集的真實點，可以是數據集范圍內的任意點。確定方法可以是隨機，也可以是人工。步驟二： 根據現有的質心集，將數據集中每個點分配到1個合適的簇里。其方法是計算每個點與每個質心的距離，為每個點找到距離最近的質心，即可分配到該質心對應的簇里。步驟三：分配完成后，重新確定每個簇里的質心，即該簇的質心更新為該簇里全部點的平均值。步驟四：重復步驟二、步驟三，直到質心集停止更新為止。此時，數據集中的全部點與對應的質心距離都為最近。上述流程可以滿足大多數普通場景的要求，但是當聚類結果以圖形等方式展現時，質心集會變得雜亂無章。此時，需要在運算過程中加入排序標準，使質心集依序排列，同時各簇也需要相應調整順序，稱作有序k-means。具體偽代碼如下。

隨機創建k個數據集范圍內的點并排序，作為初始質心。

While任意數據點改變簇分配結果

｛ for遍歷數據集里的每個數據點

｛ for遍歷每個質心

｛ 計算當前數據點與當前質心的加權歐式距離

｝

依據最近原則，重新分配每個點到新簇

｝

for遍歷每個簇

依據當前簇里的全部點，更新當前質心

｝

2.3 改進bi-kmeans

bi-kmeans的思想建立在傳統k-means的基礎上，每次只做二分化解，直到滿足指定簇數目為止。其步驟有以下2個。首先，將全部數據點視為一個簇，將當前簇一分為二。其次，選擇其中一個簇再一分為二，選擇的標準是劃分該簇以最大程度地減少平方和誤差SSE的值。重復這個劃分過程，直到簇的數目達到k為止。當傳統的bi-kmeans算法每次一分為二時，都是在質心序列尾部附加新質心。當輸出方式有圖形要求時，也會面臨與k-means一樣的問題。改進算法是在每次劃分的過程中根據質心的排序標準，將新質心插入質心序列中，稱作有序bi-kmeans。偽代碼如下。

全部點視作一個簇，即原始簇

while簇的數目lt;k

｛ for遍歷每個簇

｛ 調用有序k-means，計算當前簇二分后的總誤差

找到目標簇，并保留二分后的結果

｝

在目標簇對應的目標質點后插入一個位置，將目標質點及后面一個位置更新為二分后的兩個質點

目標簇劃分為兩個新簇

｝

3 分析過程

3.1 數據來源

某高校采用現階段流行的移動支付方式，校園內部遍布移動支付終端。消費者可以靈活選擇支付方式，包括現金支付和移動支付。由于移動支付具有便利性，幾乎無人選擇傳統的現金支付。就餐環境已經徹底拋棄現金支付，完全采用移動支付。

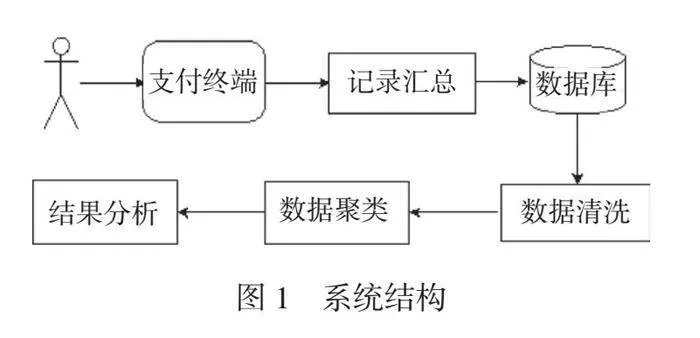
當每天學生在消費時，與支付終端的交互記錄源源不斷匯總到后臺服務器上，形成詳細的交易數據庫。在這個消費數據庫中，包括有時間、地點以及窗口等信息。通過對這些記錄進行數據挖掘，可以得到預期的聚類結果，可以分析出學生的消費習慣、消費水平等潛在信息。消費系統的結構如圖1所示。

3.2 實踐設計

全體學生消費記錄按照時間段為標準，選取該時間段內的記錄作為樣本，每個學生是一個數據點p，總共有n個學生，這些樣本全體組成數據集P，有pi∈P，i∈[1，n]。傳統的k-means算法需要給出2個初始參數：初始質心集Ce和聚類數目k。質心集Ce中有k個質心ce，即cej∈Ce，j∈[1，k]。

根據質心集Ce劃分出來的簇Cl，有CljP，j∈[1，k]。Clj的長度為nj，有nj∈[1，n]，j∈[1，k]。在迭代的過程中，Ce和Cl都處于動態的狀態。劃分簇Cl的標準為加權歐式距離，如公式（2）所示，即簇中每個數據點p到相應質心ce的距離為最近。

3.3 數據格式

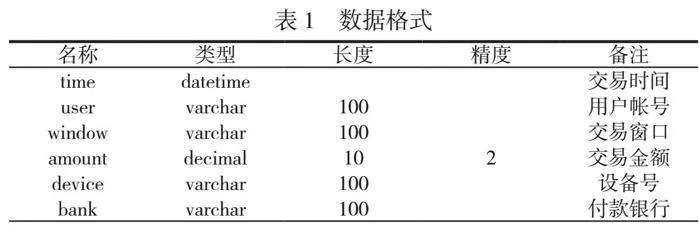
全部的消費記錄是直接進入數據庫，以最原始的格式存儲（如圖1所示）。其優點是保留了數據最初始的狀態，各項目可以根據自身的需求提取和處理原始數據。同時，缺點在于數據的原始格式不能完全滿足各項目的特定要求。因此要經歷數據的清洗階段，包括數據篩選、數據集成、類型轉換和數據歸約，然后才能進行數據的聚類。數據清洗后的格式見表1。表中為有效字段，無效字段已省略。

3.4 實踐流程

根據上述的數據來源、數據格式和實踐設計，整個實踐過程分為實踐有序k-means和實踐有序bi-kmeans。

3.4.1 實踐有序k-means

步驟一：利用質心隨機函數，在數據集P范圍內隨機生成k個質心ce，有公式（3）成立。生成后對全部質心ce排序，組成質心集Ce。

cej≤max（P） " " " " " " " " " " " " " （3）

式中：max（P）為數據集P的范圍，即數據集P各向量的最大值。

步驟二：對于每個點p來說，利用加權歐式距離公式（2），找到與之匹配的距離最近質心ce，如公式（4）所示。

min（d（pi，ce））=d（pi，cej）lt;d（pi，cel） " " " " （4）

式中：d（pi，ce）為數據點pi與質心ce間的距離；d（pi，cej）為數據點pi與質心cej間的距離；d（pi，cel）為數據點pi與質心cel間的距離，j，l∈[1，k]，并且j≠l。質心cej是距離點pi最近的質心；cel是非cej的其他任意質心。該步驟更新了每個簇的劃分，即更新每個簇里的點成員。

步驟三：每個簇更新后，更新簇里的質心，如公式（5）所示。

（5）

式中：nj為當前簇的長度，有j∈[1，k]，nj∈[1，n]。

步驟四：由于在步驟三中每個簇Clj都產生新的質心cej，為驗證當前質心集是否穩定，因此重復步驟二、步驟三，直到每個簇劃分停止更新。當前循環步驟二、步驟三的結果與上一次循環的結果一致。

3.4.2 實踐有序bi-kmeans

步驟一： 數據集P里的全部點p作為第一個簇的成員，此時Cl1=P，Clj=?，j∈[2，k]。質心集的長度為1，這個質心ce1為全部點的平均值，如公式（4）所示。此時，j=k=1，n1=n。

步驟二：對于每個不為空的簇調用有序k-means，進行二分計算，即調用時設定有序k-means的k=2。能參與二分計算的簇有Cli?P，Cli≠?，i∈[1，k]。找到二分后可以令數據集P總距離最小的簇Cla，a∈[1，k]，如公式（6）所示。

（6）

式中：d（P，Ce）為數據集P到各質心的總距離；∑d（Cl，ce）為每個簇Cl到與其匹配質心ce的距離總和；d（Cla1，cea1）和d（Cla2，cea2）為簇Cla二分后的2個簇內距離；d（Clb1，ceb1）和d（Clb2，ceb2）為簇Clb二分后的2個簇內距離，此時a≠b，Cla≠Clb，即Clb為非Cla的其他任意簇。

步驟三： 更新質心集Ce，將cea替換為cea1，并在其后插入cea2。cea1和cea2的獲取方式如公式（5）所示。此時，j=a。

步驟四： 當質心集Ce的長度小于k時，回到步驟2進行重復迭代。當質心集Ce的長度等于k時，劃分停止。此時，已經達到二分后k個質心、k個簇的要求。

4 實踐結果

每個學生每天消費3次，則總消費記錄數量應該大于學生總人數的3倍。預期的情況是學生有可能每天消費次數超過3次，同時還會有非學生的消費記錄。但是實際情況是總消費記錄數量遠小于學生總人數的3倍。因為學生可選的就餐地點眾多，不會局限于只在校內消費，所以結果是很多學生在某些時間點的消費記錄為空白。本次選取樣本的時間段為2021—2022年，即2021年9月1日—2022年8月31日。學生樣本人數超過6000人，每個學生整個學年的消費次數和消費金額進入樣本庫，記為1個點。經過初步篩選后，已經剔除極其孤立的5個點。本次實踐環境為Intel Xeon CPU E7-8880 v4 @ 2.20GHz，VMware ESXi 6.0.0，CentOS7.9.2009，Django4.1.7，mysql8.0.31，Nginx1.22.1，Plotly5.13.1。

4.1 k-means結果

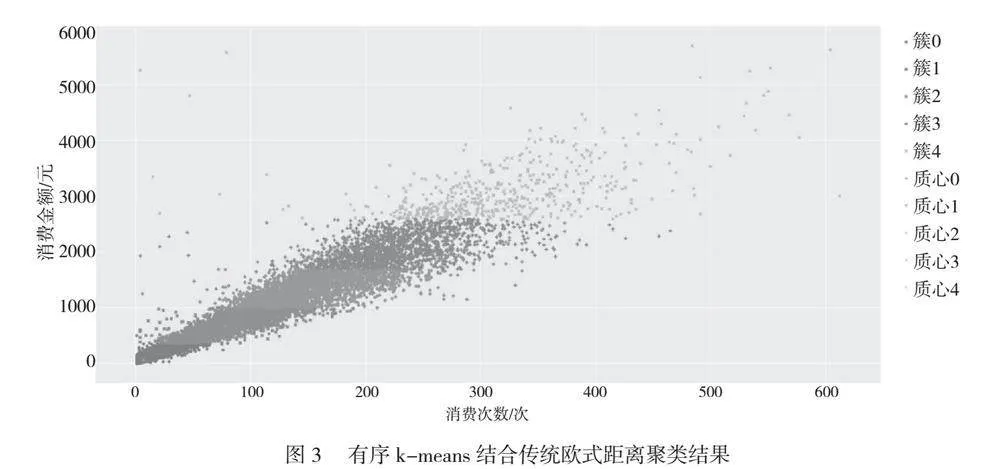
不論是傳統k-means，還是有序k-means，都需要事先提供k個初始質心。確定k個初始質心的方法可以是隨機方式，也可以是人工方式或者人工干預下的隨機方式。確定方法的選擇對分配結果的影響不大，當多次計算后會發現結果趨近一致，而對于運算的迭代次數影響很大。k值的大小是一個經驗判斷的結果，可以從1～n中任意選擇，根據項目的基本需求來確定。學生的消費能力是學生家庭生活水平的重要標準，通常校內的貧困比例為1∶5，因此，本次k值確定為k=5。傳統k-means結合傳統歐式距離聚類的結果如圖2所示。有序k-means結合傳統歐式距離聚類的結果如圖3所示。

圖2中各質心與原點的距離由近及遠依次為質心4 lt; 質心3 lt; 質心2 lt; 質心1 lt; 質心0，相應的簇順序為簇4、簇3、簇2、簇1和簇0。質心和簇這樣的亂序排列對圖片呈現結果的影響幾乎可以忽略，缺點是當需要順序分析時無法滿足要求。

有序k-means在迭代過程中，對質心成員排序。因此，在圖3中各質心到原點的距離呈現出自然數順序，各簇也相應為自然數順序。這樣的排序利于在后續研究中順暢使用。從圖2和圖3可以看出，各簇之間出現了嚴格的水平分界。其原因是各點的2個向量之間存在不同數量級別的差異。當計算傳統歐式距離時，消費金額比消費次數高1個數量級，消費金額的作用因子較大，消費次數的作用因子較小，因此各點的消費金額成為傳統歐式距離的主要影響因素，消費次數則成為可有可無的因素。

4.2 bi-kmeans結果

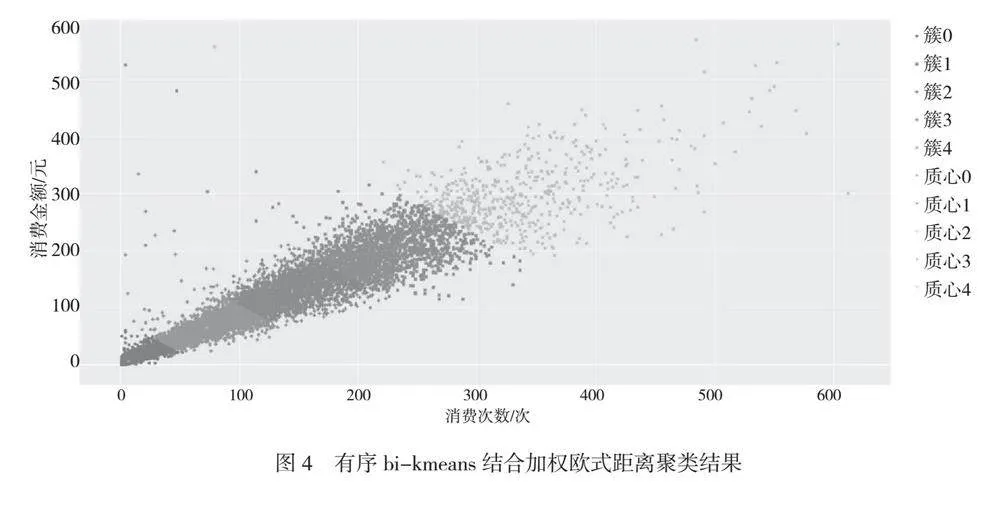
按照一致性原則，bi-kmeans的k值也確定為k=5。由于bi-kmeans的k值在迭代過程中是從1逐步增加的，并且每個質心都是由簇內點共同決定的，因此不需要在迭代之初設定初始質心。有序bi-kmeans結合加權歐式距離聚類結果如圖4所示。

由于消費金額比消費次數高1個數量級別，因此在加權歐式距離中消費金額向量的權重設定為1/10，消費次數的權重設定為1。從圖4可以看出，劃分簇邊界的決定因素不再由消費金額單獨決定，而是由消費金額和消費次數共同決定，2個決定因素的因子比例為1∶1，簇邊界的劃分由2個向量來共同決定。

簇cluster3與簇cluster4之間的邊界從圖3到圖4變化，代表有部分學生消費金額不高，因此在圖3中被劃為簇cluster3，采用加權歐式距離后這部分學生被劃入簇cluster4。顯然，這部分學生是高消費次數、低消費金額，更符合家庭貧困的要求。設定k=5的初衷在于尋找真實的貧困學生，采用有序bi-kmeans結合加權歐式距離的聚類方式是更優算法。

5 結語

高校學生在校園內部的消費行為通過移動支付，都會留下痕跡。本例采集全樣本，通過篩選、集成和轉換等系列操作后，提出有序bi-kmeans結合加權歐式距離的方式來得出聚類結果。根據聚類結果對比，得出結論為有序bi-kmeans結合加權歐式距離的算法為更優算法，可以避免傳統算法的弊端，可以找到目標學生群。優化后的聚類算法更客觀地通過學生消費行為反應出學生的消費水平，為關心學生生活的部門提供更準確的分析結果，解決人為劃分目標學生群效率低、主觀因素過重等缺點。本例中的樣本分布比較均勻，2個向量基本為正比關系且樣本量足夠大。當實踐k-means算法時，并未出現局部最優和空簇的情況。在實踐過程中，當人為縮小樣本量到足夠小時，暴露了k-means算法的缺點。改進后的bi-means算法當樣本量大和小時都表現得比較優秀。

參考文獻

[1]龔黎旰，顧坤，明心銘，等.基于校園一卡通大數據的高校學生消費行為分析[J].深圳大學學報理工版，2022，37（增刊1）：150-154.

[2]柴政，屈莉莉，彭貴賓.高校貧困生精準資助的神經網絡模型[J].數學的實踐與認識，2018，48（16）：85-91.