基于插值修正的上證50ETF期權隱含高階矩研究

摘要：期權隱含高階矩是衡量金融資產波動性和非對稱性的關鍵指標。然而，真實市場中期權的執行價格具有離散性和有界性，直接應用理論方法基于市場離散期權數據計算的隱含高階矩存在近似誤差，影響指標可靠性。本文利用上證50ETF期權數據，采用無模型方法計算隱含波動率和隱含偏度指標，并通過“內插-外推”方法進行修正。研究結果表明：①未修正的隱含高階矩通常被高估；②隱含波動率指數與上證50ETF收益之間存在顯著的負相關性，這支持了市場存在杠桿效應和波動率反饋效應的理論；③隱含偏度指數與上證50ETF收益之間存在顯著的正相關性，這可以理解為投資者更偏好右偏資產，而右偏資產價值傾向于被高估，從而導致負的收益；④在大多數時期，已實現波動率比隱含波動率低，這表明大多數投資者大部分時間傾向于規避風險，并且愿意為對沖風險支付費用。

關鍵詞：期權隱含高階矩；上證50ETF；已實現高階矩；風險溢價

一、引言

長期以來，期權價格中蘊含的信息一直是學術界和業界關注的焦點。早期研究表明，通過Black-Scholes（BS）公式可以獲得隱含波動率（Black和Scholes，1973）。隨著期權定價模型與技術手段的不斷發展，研究者發現期權面板數據中還包含了更為復雜的信息，如隱含偏度。這些期權隱含信息被廣泛認為是對真實測度下歷史信息的重要補充，因為期權價格反映了標的資產在風險中性測度下的預期走勢。本文主要探討期權的隱含信息，包括隱含波動率和隱含偏度。這兩者分別代表了風險中性測度下標的資產收益率的預期波動性和偏度。

提取期權價格中的隱含信息對學術界和業界都具有重要意義。在實際應用中，隱含信息可作為市場信號使用。例如，芝加哥期權交易所（CBOE）的市場波動率指數（VIX），通常被稱為“恐慌指數”，用于預測未來市場波動率；中國波動率指數（iVIX）用于預警市場潛在風險，并作為投資者調整倉位的重要信號。隱含偏度可以反映股票的預期未來走勢，隱含偏度值越小預示著未來資產收益分布越左偏，即資產收益出現下跌的概率會增加。除此之外，這些信息可以與真實測度下的信息結合，用于構建風險溢價指標，以反映市場預期和實際情況的偏差，從而為研究市場收益提供支持。因此，充分利用期權價格中的隱含信息可以為風險管理和金融資產定價提供有效指導。

一些重要文獻研究了期權隱含高階矩。例如，Christoffersen等（2013）總結了期權隱含信息的相關研究，介紹了兩種構建期權隱含高階矩的方法：參數方法（Heston，1993；Christoffersen等，2009）和無模型方法（Carr和Madan，1998）。相比之下，無模型方法無須依賴特定的模型設定，因此被認為更具靈活性。在實際市場中，芝加哥期權交易所就是采用無模型方法來計算VIX指數。

目前，關于期權隱含信息的研究已經取得了諸多成果。Jiang和Tian（2005）發現，無模型方法計算的隱含波動率可以更有效地預測未來實際波動率。鄭振龍等（2016）利用S&P500指數期權的方差和偏度對股票橫截面序列進行了回歸分析。叢明舒（2018）發現，中國市場和美國市場的期權隱含信息對股票收益率的影響存在顯著差異。

盡管無模型方法具有多種優勢，但仍存在一些局限性，如它依賴期權執行價格連續性的假設。然而，在實際市場中，我們只能觀察到離散的期權執行價格，因此這一假設并不成立。此外，期權執行價格的范圍是有界的，這與計算公式中的無界假設不符。為了盡可能解決這些局限性，本文在無模型方法的基礎上引入了“內插-外推”方法，以修正隱含高階矩的估算值，并將修正后的隱含高階矩信息應用于中國市場，進一步研究修正后的隱含高階矩對50ETF收益率的影響，以及隱含高階矩與已實現高階矩之間的關系。此外，本文基于風險中性測度和真實測度構建了方差風險溢價指標，并研究了該指標對50ETF收益率的影響。

本文剩余的結構安排如下：第二部分詳細介紹了隱含高階矩指標的構建方法。第三部分分析了計算隱含高階矩時近似誤差的來源。第四部分提出了近似誤差的修正方法。第五部分進行實證分析。第六部分總結本文的研究結論，并討論其在實踐中的潛在應用和意義。

二、隱含高階矩構建

從期權面板數據中計算隱含高階矩的方法主要分為有模型和無模型兩種。由于前者容易受模型不確定性的影響，故本文主要借鑒Bakshi等（2003）關于無模型方法的思想來推導期權隱含高階矩。設定R（t，τ）=lnS（t+τ）-lnS（t）為t時刻τ期的收益率，S（t）為t時刻資產的價格，則在t時刻τ期的風險中性收益率的隱含波動率和隱含偏度可以分別定義為：

Vol（t，τ）={Et［R（t，τ）-Et（R（t，τ））］2}1/2（1）

Skew（t，τ）=Et［R（t，τ）-Et（R（t，τ））］3{Et［R（t，τ）-Et（R（t，τ））］2}3/2（2）

這里，Et（·）為風險中性下的條件期望，即Et（·）=E（·|S（t））。

根據CBOE白皮書、Bakshi等（2003）以及Bali和Murray（2013）的研究，可以通過虛值期權數據推導出對應資產的隱含高階矩：

Vol（t，τ）=（erτV（t，τ）-μ（t，τ）2）1/2（3）

Skew（t，τ）=erτW（t，τ）-3μ（t，τ）erτV（t，τ）+2μ（t，τ）3［erτV（t，τ）-μ（t，τ）2］3/2（4）

其中，μ（t，τ）=erτ-1-erτ2V（t，τ）-erτ6W（t，τ）-erτ24X（t，τ），r為無風險利率，τ為期權到期期限。隱含高階矩中對應的函數V、W和X的具體形式如下：

V（t，τ）=∫∞S（t）21-lnKS（t）K2C（t，τ;K）dK+∫S（t）021+lnS（t）KK2P（t，τ;K）dK（5）

W（t，τ）=∫∞S（t）6lnKS（t）-3lnKS（t）2K2C（t，τ;K）dK-∫S（t）06lnS（t）K+3lnS（t）K2K2P（t，τ;K）dK（6）

X（t，τ）=∫∞S（t）12lnKS（t）2+4lnKS（t）3K2

C（t，τ;K）dK+∫S（t）012lnS（t）K2+4lnS（t）K3K2P（t，τ;K）dK（7）

其中，C（t，τ;K）和P（t，τ;K）分別是t時刻開始t+τ時刻到期且執行價格為K的看漲和看跌期權價格。

為了計算V、W和X，需要使用連續執行價格下的看漲和看跌期權的價格。然而，由于期權面板數據是離散的，只能利用離散的期權數據計算V、W和X。

V︿（t，τ）=∑nci=121-lnKciS（t）*Kci2C（t，τ;Kci）△Kci+∑npi=121+lnS（t）*KpiKpi2P（t，τ;Kpi）△Kpi（8）

W︿（t，τ）=∑nci=16lnKciS（t）*-3lnKciS（t）*2Kci2C（t，τ;Kci）△Kci-∑npi=16lnS（t）*Kpi+3lnS（t）*Kpi2Kpi2P（t，τ;Kpi）△Kpi（9）

X︿（t，τ）=∑nci=112lnKciS（t）*2+4lnKciS（t）*3Kci2C（t，τ;Kci）△Kci+∑npi=112lnS（t）*Kpi2+4lnS（t）*Kpi3Kpi2P（t，τ;Kpi）△Kpi（10）

這里，S（t）*=S（t）-PVDivs為除息后的股價，PVDivs為股息現值，Kci和Kpi分別為第i個虛值看漲期權和看跌期權的行權價，C（t，τ;Kci）和P（t，τ;Kpi）分別為第i個看漲和看跌期權的價格，nc和np分別為看漲和看跌期權的數量，對于2≤i≤nc，△Kci=Kci-1-Kci，△Kc1=S*t-Kc1，對于2≤i≤np，△Kpi=Kpi-1-Kpi，△Kp1=S*t-Kp1。這樣通過離散方法可以計算出隱含波動率和隱含偏度。

為了估計無模型隱含高階矩，式（8）～式（10）中給出的離散近似V︿、W︿和X︿會產生多種近似誤差，如截斷誤差和離散化誤差。這些誤差可能對估計隱含高階矩產生重要影響。接下來，將詳細介紹每種近似誤差。

三、近似誤差來源

在本節中，筆者將探討在利用離散期權數據計算隱含高階矩時產生的兩種近似誤差，即截斷誤差和離散化誤差。

（一）截斷誤差

截斷誤差是由于執行價格K范圍有界導致的。正如V、W和X的定義所示，無模型隱含高階矩的計算需要0到無窮的執行價格，然而，當使用離散化的數據進行計算時，只能利用有限范圍的執行價格數據。記KL和KU分別是給定期限的最低和最高執行價格。由于無限范圍的執行價格被有限范圍的執行價格［KL，KU］所取代，因此可以得到以下近似式（先不考慮給定范圍內的離散情況）：

V（t，τ）≈∫KUS（t）21-lnKS（t）K2C（t，τ;K）dK+∫S（t）KL21+lnS（t）KK2P（t，τ;K）dK（11）

W（t，τ）≈∫KUS（t）6lnKS（t）-3lnKS（t）2K2C（t，τ;K）dK-∫S（t）KL6lnS（t）K+3lnS（t）K2K2P（t，τ;K）dK（12）

X（t，τ）≈∫KUS（t）12lnKS（t）2+4lnKS（t）3K2C（t，τ;K）dK+∫S（t）KL12lnS（t）K2+4lnS（t）K3K2

P（t，τ;K）dK（13）

因此，V、W和X的截斷誤差由以下表達式給出：

Vtrunc=-∫∞KU21-lnKS（t）K2C（t，τ;K）dK+∫KL021+lnS（t）KK2P（t，τ;K）dK（14）

Wtrunc=-∫∞KU6lnKS（t）-3lnKS（t）2K2C（t，τ;K）dK-∫KL06lnS（t）K+3lnS（t）K2K2

P（t，τ;K）dK（15）

Xtrunc=-∫∞KU12lnKS（t）2+4lnKS（t）3K2

C（t，τ;K）dK+∫KL012lnS（t）K（t）2+4lnS（t）K3K2

P（t，τ;K）dK（16）

負號表明截斷誤差會導致計算的高階矩產生負的偏差。

（二）離散化誤差

離散化誤差是由于數值積分導致的，因為CBOE在計算中采用式（8）、式（9）、式（10）。盡管從理論上看，數值積分誤差可以通過使用足夠精細的執行價格網絡來最小化，但實際期權面板數據中可獲取的離散數據始終是有限的，且行權價之間的離散程度往往很大，因此會產生較為明顯的離散化誤差。離散化誤差可以表示為：

Vdisc=V︿（t，τ）-∫KUS（t）21-lnKS（t）K2C（t，τ;K）dK+∫S（t）KL21+lnS（t）KK2P（t，τ;K）dK（17）

Wdisc=W︿（t，τ）-∫KUS（t）6lnKS（t）-3lnKS（t）2K2C（t，τ;K）dK-∫S（t）KL6lnS（t）K+3lnS（t）K2K2

P（t，τ;K）dK（18）

Xdisc=X︿（t，τ）-∫KUS（t）12lnKS（t）2+4lnKS（t）3K2C（t，τ;K）dK+∫S（t）KL12lnS（t）K2+4lnS（t）K3K2

P（t，τ;K）dK（19）

四、近似誤差的處理

近似誤差主要由于期權數據在不同執行價格下的稀疏性引起。為了減少這種誤差，需要獲取更多執行價格對應的期權價格數據。解決這一問題的一種方法是通過“平滑”技術填補稀疏的期權數據。通常而言，“平滑”技術應用于期權合約的波動率，而非直接應用于期權價格。具體步驟如下：首先，利用BS公式計算已有期權價格對應的波動率；其次，使用“平滑”技術構建期權合約對應的波動率曲線，以獲取所需執行價格對應的波動率；最后，再次利用BS公式計算相應執行價格的看漲和看跌期權價格。本文采用了一種有效的平滑方法來提取無模型波動率，即采用“內插-外推”方法構建波動率曲面。

（一）已有執行價格間的內插法

假定對于給定的到期日T有N個執行價格，分別為Ki，i=1，2，…，N，其對應的看漲看跌期權的市場價格分別是CM（Ki，T）和PM（Ki，T）。不失一般性，有0<KL=K1<K2<…<KN=KU<∞。這里僅使用OTM期權來建立波動率函數。通過BS模型，結合N個執行價格以及對應的期權價格，可以反推出這N個執行價格對應的波動率（σ（Ki，T），i=1，2，…，N）。

構建執行價格區間［KL，KU］上的波動率函數是關鍵。已有研究中，參數法和非參數法都被廣泛應用（Bahra，2007；Bliss和Panigirtzoglou，2002；Anagnou等，2002）。然而，參數方法對模型形式的限制，無法靈活適應觀測數據。因此，本文采用非參數方法來構建波動率函數，以便更好地處理和利用不同執行價格下的期權價格數據。

采用“內插法”在N個執行價格之間建立光滑函數，可以很好地擬合這N個已知的波動率。筆者希望在執行價格區間［KL，KU］找到一個可微函數f（K），有

f（Ki）=σ（Ki，T），i=1，2，…，N（20）

這里參考Jiang和Tian（2005），使用三次樣條來擬合已知的波動率。為了使擬合結果更好，從K2到KN-1所有的內部執行價格均被用作節點來擬合三次樣條。接著，對于新的內插點便可以通過f（K）獲得其對應合約的波動率。

（二）已有執行價格外的外推法

由于在已列出的執行價格區間之外，沒有已知的期權價格，而范圍更廣的執行價格對于計算隱含高階矩有較大的好處，因此需要根據已構建的波動率函數對區間外的波動率進行外推。具體來說，考慮兩種外推方法。

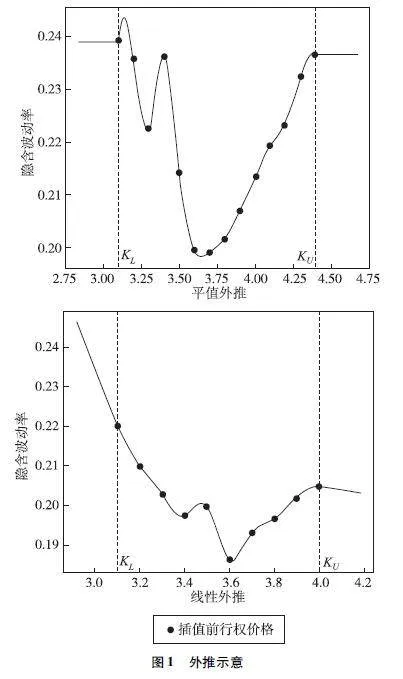
1平推法

平推法是指對于執行價格區間外的波動率，用最接近的已知波動率值來代替，即對于區間（0，KL］的波動率都用σ（KL）來代替，對于區間［KU，∞）的波動率都用σ（KU）來代替，其核心思想如圖1上圖所示，該方法常被用于波動率估計的修正。然而，“平推法”存在兩個缺點：一是為了滿足無套利條件，波動率函數需要保持連續性，但是“平推法”可能導致波動率函數在KL和KU處出現拐點，從而使風險中性概率密度函數變為負數；二是根據波動率“微笑”或者波動率“偏斜”的觀察，隨著執行價格遠離當前股價，波動率往往會上升。因此，對于執行價格區間外的波動率使用常數波動率代替，可能會導致波動率被低估。

2線性外推法

線性外推法指的是在最低KL和最高KU的執行價格點上施加平滑條件，并保持一個線性的外推結構。具體來說，通過調整處于執行價格兩邊的線性外推斜率，使其與最低KL或最高KU執行價格內部端的斜率一致，如圖1下圖所示。這種方法確保了在整個執行價格范圍內都有平滑的波動率曲線，并且能夠很好地擬合已知的波動率數據。“線性外推法”構建的波動率曲線更符合通常觀察到的波動率“微笑”或者波動率“偏斜”。

由此可見，一旦構建好波動率函數，適當范圍內任意執行價格處的期權價格都可以通過使用BS模型根據相應擬合的波動率計算得到。這樣一來，可以利用更多的期權數據對數值積分V、W和X進行離散化計算。

五、實證分析

（一）數據描述

本文選取2021年1月4日至2021年12月31日每天9：30到11：30以及13：00到15：00的50ETF指數和50ETF期權的1分鐘級數據，共計243天（交易日），每天包含241個1分鐘數據。剔除所有不滿足無套利條件的期權樣本，選擇期權到期期限為10～60天，并且每天至少存在兩支認購和認沽期權的樣本。當數據處理完后，可以使用前面章節的方法計算出風險中性高階矩，這里所計算的均為期限τ為30天的風險中性矩。

（二）修正方案間的比較分析

采用CBOE的指標構建方法，分別構建波動率指數和偏度指數：

iVIXt，τ=100*Volt，τ（21）

iSKEWt，τ=100-10*Skewt，τ（22）

本節對比分析了不同的“內插-外推”方法對50ETF波動率指數（iVIX）和偏度指數（iSKEW）的影響。鑒于截斷誤差和離散化誤差，對不同方法進行比較分析，以評估其對iVIX和iSKEW的影響。對“內插-外推”方法進行兩種不同的內插點數選擇，分別為在已有執行價格區間內選擇100個和500個等間距內插點。在內插計算完成后，還采用了線性外推和平值外推兩種方法。對于線性外推，當內插點數為100時，考慮2個、10個和20個等間距外推點；當內插點數為500時，則考慮10個、50個和100個等間距外推點，以確保外推的區間長度一致。對于平值外推，外推點個數的選擇與線性外推方法一致。

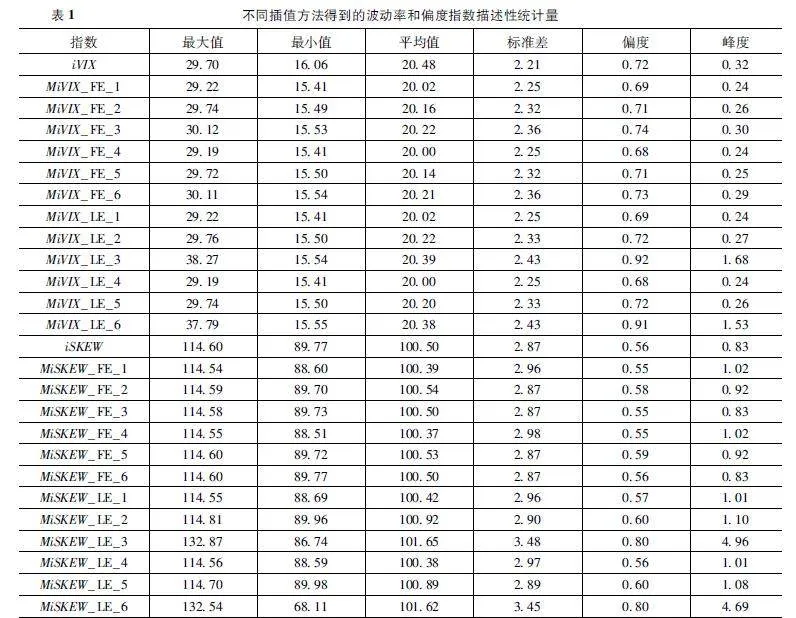
表1展示了不同插值方法計算的波動率指數和偏度指數的描述性統計。筆者觀察到修正后的iVIX指數相對于未修正的iVIX指數，在均值和最小值上幾乎都顯示出下降趨勢。具體而言，平值外推方法得到的iVIX指數相對于線性外推方法更小，且內插點數為500時的iVIX指數比內插點數為100時的iVIX指數要小。對于iSKEW的計算，平值外推對其影響不大。然而，當線性外推點數過多時會導致iSKEW值顯著增加。

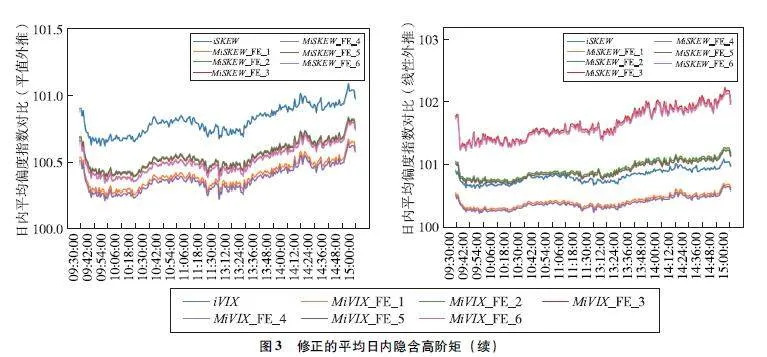
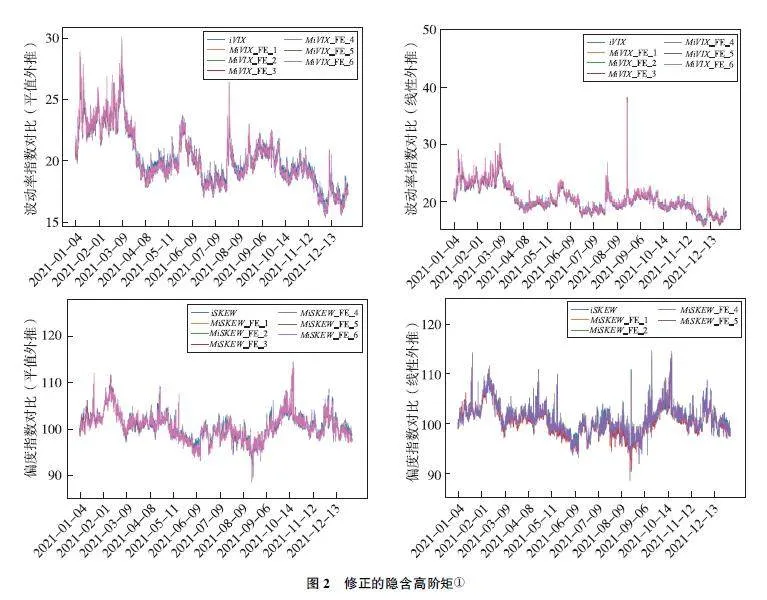
圖2呈現了不同插值方法修正后的iVIX和iSKEW指數的時間序列。可以發現，未插值情況下的波動率和偏度指數一般位于所有插值計算結果之上，顯示出插值后的指數普遍偏低。此外，線性外推點數過多可能會產生異常值。為了更好地顯示不同方法之間的差異，圖3展示了不同插值方法修正后的iVIX和iSKEW指數的平均日內走勢。可以發現，對于平均日內iVIX指數，經過平值外推和線性外推修正后的波動率指數均低于未插值計算結果，且內插點數對其影響較小，而外推點數對其影響較大。對于平均日內iSKEW指數，平值外推修正的iSKEW指數低于未插值的計算結果。然而，線性外推修正的iSKEW指數在外推點數過多時會顯著高于未插值的計算結果。因此，不建議使用過多的線性外推點數。

綜上所述，未插值的隱含高階矩往往存在高估的情況，這可能導致市場投資者在期權交易、金融資產定價、資產收益分析以及金融風險傳染度量等方面做出錯誤的決策。并且內插點數越多，適度的線性外推結果越穩健。由于理論上采用插值計算的隱含高階矩更為準確，且實證結果顯示插值和不插值結果差異比較大。基于這些考量，選擇了內插點數為500、外推點數為50的方案進行后續數據分析和實證研究。

（三）變量的描述性統計

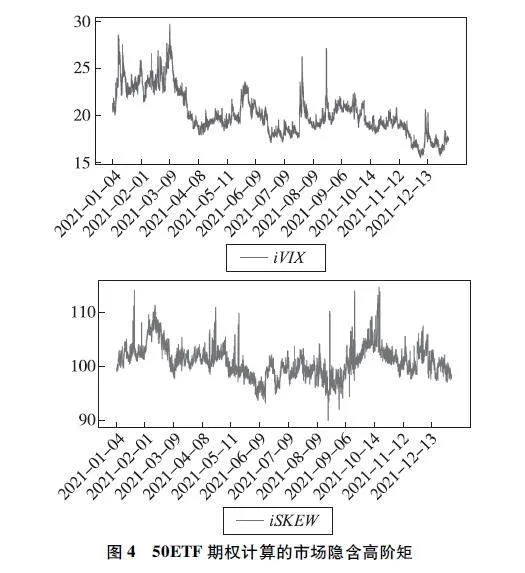
圖4分別展示了修正后的iVIX指數和iSKEW指數的時間序列。以下是對圖4結果的分析：①從iSKEW指數圖中可以觀察到，2021年中國市場的iSKEW指數有部分數值小于100，處于90～100，顯示出市場預期收益率出現右偏的現象。這與Chang等（2013）在美國市場計算的隱含偏度指數始終

大于100有所不同。②iSKEW指數通常在達到115之后會下跌，而不是持續上升，這是因為市場上存在套利機會的投資者，他們的介入會使iSKEW指數回歸其均值附近，從而避免持續的左偏現象。這些分析結果揭示了市場波動率和偏度指數在不同時間段的動態變化，對理解市場行為和制定投資策略具有重要意義。

圖5顯示了以下內容：左側為iVIX指數和iSKEW指數本身的自相關圖；右側則展示了對iVIX指數和iSKEW指數進行差分后的自相關圖。在自相關圖中，陰影部分表示95%的置信區間。觀察圖可知，iVIX指數和iSKEW指數本身具有顯著的自相關性，然而，經過一階差分處理后，大部分iVIX指數和iSKEW指數的自相關系數均落在95%的置信區間內。這表明對隱含高階矩進行差分處理后的時間序列更加平穩。

（四）回歸分析

1收益率回歸分析

Jondeau等（2019）在其研究中使用美國數據發現，偏度可以影響個股的收益率。Harvey和Siddique（2000，2000）的研究結果顯示，偏度不僅影響個股的收益率，還對整個股票市場的收益率產生影響。那么，在中國市場，隱含高階矩是否會對50ETF的收益率產生影響呢？

為了研究隱含高階矩對上證50ETF指數收益的影響，本節使用了差分后的iVIX指數、iSKEW指數及其組合對上證50ETF指數的收益率進行回歸分析。研究數據覆蓋了2021年1月4日至2021年12月31日的243個交易日的50ETF和期權數據。我們建立了以下三個模型：

Model1：Rt=α+β1△iVIXt+t（23）

Model2：Rt=α+β2△iSKEWt+t（24）

Model3：Rt=α+β1△iVIXt+β2△iSKEWt+t（25）

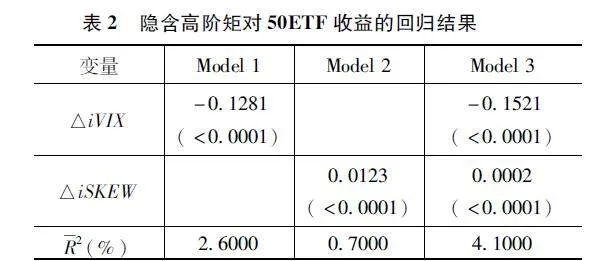
這里的Rt是第t個時刻50ETF的對數價格收益率，△iVIXt=iVIXt-iVIXt-1，△iSKEWt=iSKEWt-iSKEWt-1。表2展示了隱含高階矩與市場收益率回歸的結果。

從表2的回歸結果可以得出：①收益率與△iVIX之間表現出顯著的負相關性，這種關系主要是由于杠桿效應和波動率反饋效應所導致的。②△iSKEW對收益率具有顯著的預測能力，這可以理解為投資者更偏好右偏的資產，而右偏的資產往往被高估，從而導致負的收益。此外，當iSKEW>100時，表明資產收益存在左偏的可能性，進一步指示資產收益下跌的風險增加。由于風險厭惡的投資者會尋求更多的風險補償來規避尾部風險的影響，因此更高的△iSKEW通常伴隨著更高的資產收益。③當△iVIX和△iSKEW同時加入收益率的回歸模型后，它們對收益率的影響依然顯著。這表明，從期權數據中提取的隱含高階矩均包含了影響50ETF收益率的重要信息。

2已實現高階矩之間的回歸分析

通過期權數據計算的隱含波動率指數和隱含偏度指數間接反映了投資者對市場風險的度量，而已實現波動率（RV）和已實現偏度（RSkew）是直接通過50ETF收益率數據計算的，能夠直接反映資產的收益情況，因此它們之間存在一定的關聯。在本節中，建立已實現高階矩與隱含高階矩之間的回歸模型，并分析它們之間的關系。首先，根據Andersen和Bollerslev（1998）及后續文獻提出的方法，構建已實現高階矩：

RVt=∑N～i=0R2t-i（26）

RSkewt=N～∑N～i=1R3t-i（RVt）3/2（27）

RSKEWt=100-10×RSkewt（28）

這里，Rt-i表示第t-i時刻的對數收益率。使用滑動步長為1分鐘，窗寬大小N～為240分鐘的數據集來計算高頻RV和RSkewt。接下來，建立已實現高階矩與隱含高階矩之間的回歸關系模型：

RV2t=α+βiVIX2t+t（29）

RSKEWt=α+βiSKEWt+t（30）

使用修正后的隱含波動率指數和隱含偏度指數，得到的回歸結果如下：

RV2t=-00294+15606iVIX2t（-969840）（2187779）（31）

RSKEWt=1570276-05636iSKEWt

（595898）（-215865）（32）

其中括號內為各個系數的t-統計量。從隱含高階矩對已實現高階矩的回歸結果可以看出：①已實現波動率和iVIX指數之間存在顯著的正相關關系；②已實現偏度指數與iSKEW指數之間存在顯著的負相關關系。由此可以說明50ETF期權隱含信息對50ETF收益率的方差和偏度具有一定的解釋作用。

3方差風險溢價回歸分析

已實現波動率反映了投資者對市場真實風險的度量，而隱含波動率則反映了對未來波動率風險的預期。因此，方差風險溢價（VRP）可以定義為在風險中性測度下的方差減去真實測度下的已實現方差，即VRPt=iVIX2t-RV2t。VRP在一定程度上反映了投資者的風險規避程度。圖6展示了高頻已實現波動率（RV）和隱含波動率（iVIX）的時間序列，可以觀察到在許多時段，iVIX比RV要大。

圖7呈現了方差風險溢價。可以看出，VRP大多時候都是大于0的，這說明中國投資者更傾向于規避風險。當未來市場走向不確定增加時，投資者規避風險的意愿會增強，導致VRP處于一個較高的水平。然而，當市場出現高波動（如2021年2月以及2021年7月）時，VRP會出現很大的負值。這表明在這些時期，市場相對較為動蕩，導致真實市場中由50ETF價格直接計算的已實現波動率要高于投資者的預期波動率。

Bollerslev等（2009）使用美國數據發現VRP在對季度收益率的預測上表現最為強烈；Qiao等（2024）則利用9個新興市場的指數構建VRP，發現VRP可以預測股指收益、貨幣收益以及資本流動，并且在短期內預測效果尤其顯著。本節利用插值的隱含波動率指數計算VRP，并研究其對上證50ETF收益率的影響。建立以下回歸模型：

Rt=α+βVRPt+t（33）

其中，Rt表示第t個時刻50ETF的對數價格收益率，VRPt表示第t個時刻的方差風險溢價。得到的回歸結果如下：

Rt=-00744+57866VRPt

（-03819）（05615）（34）

括號內為參數估計的t-統計量。回歸結果顯示，截距項和斜率項在95%置信水平下均不顯著，表明VRP對上證50ETF的收益率沒有顯著的影響，這與田鳳平和楊科（2021）的研究結果一致。

六、結論

本文利用上證50ETF及其期權數據，采用“內插-外推”方法，計算了50ETF指數的風險中性隱含高階矩，并將其與基于CBOE白皮書未插值計算的隱含高階矩進行了比較。結果顯示，未插值處理的隱含波動率指數和隱含偏度指數都存在一定程度的被高估。隱含波動率的被高估通常意味著期權價格可能也被高估，這可能誤導依賴隱含波動率指數進行期權交易的投資者，從而導致損失。鑒于國內期權市場近年來的快速發展，精確構建隱含波動率和偏度指標對維護投資者信心和衍生品市場的穩定發展至關重要。因此，本文建議采用基于“內插-外推”方法修正的隱含波動率和隱含偏度作為新的研究指標。

同時，本文還研究了插值后的隱含高階矩信息對50ETF收益率以及已實現高階矩的影響，并進一步基于隱含高階矩構建了方差風險溢價，分析其對50ETF收益率的影響。研究發現，隱含高階矩與50ETF收益率之間存在顯著的相關性。一方面，隱含波動率指數和收益率之間的負相關性為中國市場可能存在杠桿效應和波動率反饋效應提供了一定的實證依據。另一方面，隱含偏度指數與收益率之間的正相關性在一定程度上說明了當市場投資者更偏好右偏資產時，由于這類資產被高估，可能導致負收益。此外，本文還發現已實現高階矩與隱含高階矩之間存在顯著的相關性，這表明50ETF期權隱含信息對50ETF收益率的方差和偏度具有一定的解釋作用。對于方差風險溢價，筆者發現市場平靜期間，隱含波動率通常高于已實現波動率，表明中國投資者大部分時間在規避風險，并且愿意為對沖風險支付費用。同時，研究發現中國市場的方差風險溢價對收益率的影響并不顯著。

綜上所述，投資者在制定投資策略時應充分考慮期權隱含的高階矩風險信息，并合理配置資產。同時，監管部門也應關注期權隱含的高階矩風險，以便更好地管理衍生品市場的風險。

參考文獻

［1］ANAGNOUI，BEDENDOM，HODGESSD，etalTherelationbetweenimpliedandrealisedprobabilitydensityfunctions［J］SSRNElectronicJournal，2002

［2］ANDERSENTG，BOLLERSLEVTAnsweringtheskeptics：Yes，standardvolatilitymodelsdoprovideaccurateforecasts［J］InternationalEconomicReview，1998，39（4）：885-905

［3］BAHRABImpliedrisk-neutralprobabilitydensityfunctionsfromoptionprices：Acentralbankperspective［J］ForecastingVolatilityintheFinancialMarkets（ThirdEdition），2007：201-226

［4］BAKSHIG，KAPADIAN，MADANDStockreturncharacteristics，skewlaws，andthedifferentialpricingofindividualequityoptions［J］TheReviewofFinancialStudies，2003，16（1）：101-143

［5］BALITG，MURRAYSDoesrisk-neutralskewnesspredictthecross-sectionofequityoptionportfolioreturns？［J］JournalofFinancialandQuantitativeAnalysis，2013，48（4）：1145-1171

［6］BLISSRR，PANIGIRTZOGLOUNTestingthestabilityofimpliedprobabilitydensityfunctions［J］JournalofBankingandFinance，2002，26（2-3）：381-422

［7］BLACKF，SCHOLESMThepricingofoptionsandcorporateliabilities［J］JournalofPoliticalEconomy，1973，81（3）：637-654

［8］BOLLERSLEVT，TAUCHENG，ZHOUHExpectedstockreturnsandvarianceriskpremia［J］TheReviewofFinancialStudies，2009，22（11）：4463-4492

［9］CHANGBY，CHRISTOFFERSENP，JACOBSKMarketskewnessriskandthecrosssectionofstockreturns［J］JournalofFinancialEconomics，2013，107（1）：46-68

［10］HARVEYCR，SIDDIQUEAConditionalskewnessinassetpricingtests［J］TheJournalofFinance，2000，55（3）：1263-1295

［11］HARVEYCR，SIDDIQUEATime-varyingconditionalskewnessandthemarketriskpremium［J］ResearchinBankingandFinance，2000，1（1）：27-60

［12］JIANGGJ，TIANYSExtractingmodel-freevolatilityfromoptionprices：AnexaminationoftheVIXindex［J］TheJournalofDerivatives，2007，14（3）：35-60

［13］JIANGGJ，TIANYSThemodel-freeimpliedvolatilityanditsinformationcontent［J］TheReviewofFinancialStudies，2005，18（4）：1305-1342

［14］JONDEAUE，ZHANGQ，ZHUXAverageskewnessmatters［J］JournalofFinancialEconomics，2019，134（1）：29-47

［15］CARRP，MADANDTowardsatheoryofvolatilitytrading［J］Volatility：Newestimationtechniquesforpricingderivatives，1998（29）：417-427

［16］CARRP，WULVarianceriskpremiums［J］TheReviewofFinancialStudies，2009，22（3）：1311-1341

［17］CHRISTOFFERSENP，JACOBSK，CHANGBYForecastingwithoptionimpliedinformation［J］HandbookofEconomicForecasting，2013，2（A）：581-656

［18］CHRISTOFFERSENP，HESTONS，JACOBSKTheshapeandtermstructureoftheindexoptionsmirk：Whymultifactorstochasticvolatilitymodelsworksowell［J］ManagementScience，2009，55（12）：1914-1932

［19］QIAOF，XUL，ZHANGX，etalVarianceriskpremiumsinemergingmarkets［J］JournalofBanking&Finance，2024（167）：107259

［20］HESTONSLAclosed-formsolutionforoptionswithstochasticvolatilitywithapplicationstobondandcurrencyoptions［J］TheReviewofFinancialStudies，1993，6（2）：327-343.

［21］叢明舒中國場內期權市場研究——基于中美關于期權隱含方差的差異［J］金融研究，2018（12）：189-206

［22］李志勇，余湄，汪壽陽方差風險溢價和收益率預測：來自上證50ETF期權市場的證據［J］系統工程理論與實踐，2022，42（2）：306-319

［23］田鳳平，楊科我國商品期貨的無模型隱含方差與方差風險溢價研究基于豆粕和白糖的分析［J］系統工程理論與實踐，2021，41（8）：2015-2029

［24］王琳玉，倪中新，郭婧上證50ETF隱含高階矩風險對股票收益的預測研究［J］統計研究，2020，37（12）：75-90

［25］鄭振龍，孫清泉，吳強方差和偏度的風險價格［J］管理科學報，2016，19（12）：110-123