感悟數學思想方法　促進數學知識建構

【摘要】在小學階段，教師需關注與該階段的數學知識密切相關的數學思想方法，以數學知識的建構為明線，以數學思想方法的感悟為暗線，讓知識建構和思想方法感悟相互促進，使學生更好地理解和掌握數學知識，更好地感受數學的思想和精髓。

【關鍵詞】小學數學；數學思想方法；“分數的意義”

【基金項目】本文系江蘇省教育學會“十三五”教育科研規劃重點課題“小學數學綜合與實踐活動中項目化學習的實踐研究”（立項編號：19A21J3ZJ8）的階段性研究成果之一。

作者簡介：季正偉（1985—），男，江蘇省鎮江市揚中市崇德小學。

數學作為一門基礎學科，其思想方法在知識建構中起著至關重要的作用。數學思想方法是現實世界的空間形式和數量關系反映到人們的意識之中，經過思維活動而產生的結果。同時，它是聯系數學知識的紐帶［1］。數學思想方法有助于培養學生的思維能力，提高學生的分析和判斷能力。而感悟數學思想方法的過程會對學生的學習和生活產生深遠影響。在數學學習中，學生需要通過對數學思想方法的運用，逐漸構建自己的數學知識體系。這樣，學生可以更深入地理解數學的本質，從而更好地掌握數學知識。

在小學數學教學中，數學思想方法的運用對于培養學生的數學思維、提高學生解決問題的能力具有重要意義。不過，單純講數學思想方法是抽象空洞的。只有將數學思想方法和具體知識相結合，讓學生在理解和運用數學知識的同時，體會和領悟數學思想，才能取得較好的效果。五年級學生學習“分數的意義”之前，在三年級已經初步認識了分數；學完“分數的意義”之后，還將學習分數的運算和實際問題的求解。“分數的意義”這一課中的相關概念比較抽象，加之學生的思維以具體形象思維為主，如果教師僅僅灌輸相關概念，而沒有留出充足的時間讓學生去操作體驗，學生往往無法做到真正理解。對此，在教學“分數的意義”這一課時，教師基于教材，創設有利于學生獲得感悟的學習情境，通過分類、抽象、數形結合、比較等數學思想方法的滲透，讓學生對相關概念由感性認識上升到理性認識，掌握分數的意義，進而促進學生學習能力的提升。

一、分類整理，建構新知

分類是根據事物間性質的相同點和不同點進行歸類的過程。單位“1”的概念是概括分數意義的關鍵，需要學生感受到生活中會被平均分的對象非常多，并在此基礎上經歷分類的過程。這有助于讓學生更好地建立認知結構。

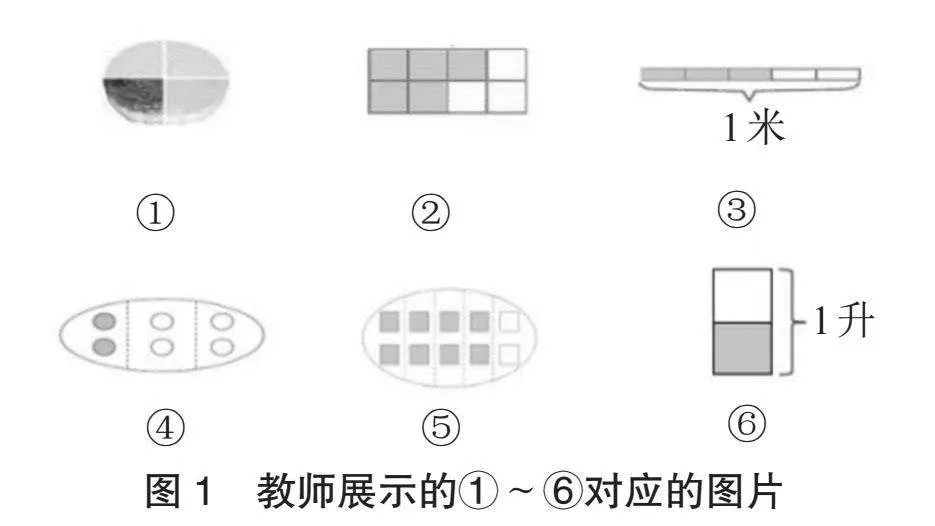
師：請用分數來表示①～⑥對應的圖片（如圖1所示）中的涂色部分，并說說每個分數的含義。

師：經過對圖片的仔細觀察，你能根據被平均分的不同對象，把它們進行分類嗎？

生1：我認為①、②、③、⑥是一類，④、⑤是一類。因為①、②、③、⑥是把圖形本身平均分，④、⑤是把一些圖形平均分。

生2：我覺得對于①、②、③、⑥，③、⑥可以單獨分為一類，因為③、⑥是基于一個單位來平均分的，而①、②是對一個物體進行平均分。

師：（板書“一個物體、一個計量單位、一個整體”）經過討論，①～⑥對應的圖片可以分成三類，而它們都可以用自然數1來表示，也就是單位“1”。

已經積累用分數表示涂色部分的經驗的學生在探究各個分數的含義的過程中，對單位“1”有了感性的認識，知道了這些分數都是把對象平均分后得到的。教師引導學生把關注點放在被平均分的對象上，進而認識到被平均分的可以是一個物體、一個計量單位、由許多物體組成的一個整體。然后，教師引導學生抽象出單位“1”的概念，并通過舉例加深對這個概念的認識。可見，學生通過分類整理，可以很好地建構單位“1”的概念；通過教師滲透的分類思想，可以為之后的學習做好鋪墊。

二、抽象概括，歸納分數的意義

抽象是舍棄非本質屬性、抽取本質屬性的過程。為了讓學生準確地認識概念，明確概念的內涵與外延，教師需要創設學習的情境，提供學習的資源，引領學生真正經歷分數意義的抽象概括過程。初步體會抽象的方法，有助于逐步提高學生的思維水平，增強學生分析問題的能力。

師：請大家觀察屏幕上的3幅圖（如圖2所示），并用涂色的方式，在每幅圖中表示出“”。這3幅圖中的單位“1”相同嗎？每幅圖中的單位“1”分別是什么？

生3：不相同。這3幅圖中的單位“1”分別是3個桃子、6個桃子、12個桃子。

師：為什么單位“1”不同，卻都能用“”表示呢？

生4：因為是把單位“1”平均分成3份、表示這樣的2份的數。

師：下面請同桌之間相互合作，一個人說分數，另一個人說它的意義，然后一起想想什么是分數。（讓學生開展活動并進行匯報）看來“把單位‘1’平均分成若干份、表示這樣的一份或幾份的數”就叫作“分數”。

一個數學概念的形成不是一蹴而就的，而是遵循學生的認知規律的。在教學分數的意義的過程中，教師讓學生異中求同，并在動手操作中發現屏幕上的3幅圖中的單位“1”不同，但“”的意義都是相同的。在此基礎上，教師讓學生舉出其他分數，進而歸納出分數的意義。這樣的學習能讓學生很好地體會知識的內涵，同時了解知識的抽象方法。

三、數形結合，理解分數單位

數形結合可以化抽象為直觀、化直觀為精確［2］。對于分數單位的概念，部分教師在教學中往往一帶而過。實際上，為了幫助學生真正理解這個概念，教師需要利用數形結合的方式，讓學生直觀感受到所有分數都是由若干個分數單位組成的。這樣能讓學生發現分數單位的本質，同時感悟數形結合的思想方法。

師：如果把屏幕上展示的這個圓形（如圖3所示）看作單位“1”，那么涂色部分就可以用“”來表示。如果把單位“1”平均分成8份，那么表示這樣的1份的數就是。從“”“”“”這幾個分數單位中，你發現了什么？并想一想什么是分數單位。

生5：我發現這幾個分數單位的分子都是“1”。

生6：我覺得“把單位‘1’平均分成若干份，表示

這樣的一份的數”就是“分數單位”。

正所謂“數缺形時少直觀，形少數時難入微”，教師在介紹分數單位時，利用直觀的圖片，讓學生深刻體會到分數單位的內涵［3］。同時，學生可以知道分數單位不像整數和小數的計數單位那樣是固定的。如此，學生能夠進一步理解分數單位的概念，在知識和自身的思維之間架起一座橋梁。

四、比較分析，分層練習

比較是對兩個或多個事物進行對比、辨析的過程，也是運用數學思維的環節，還是一種重要的數學思想方法。比較異同可以培養學生的觀察能力、分析能力和判斷能力，同時有助于增強學生思維的嚴謹性和表達的精確性。教師在布置分層練習時運用比較的方法，可以讓學生全面、準確地認識分數的意義。

師：我們知道整數、小數可以用數軸上的點來表示，那分數可以嗎？請觀察屏幕上的2條數軸（如圖4所示），試著回答為什么2條數軸上用小圓點標記的位置分別用“”和“”來表示。

生7：因為第一條數軸中“0”到“1”的距離被看作是單位“1”，將單位“1”平均分成3份，其中1份可以用“”來表示；第二條數軸中“0”到“1”的距離被看作是單位“1”，將單位“1”平均分成6份，其中2份可以用“”來表示。

師：是的，“”“”這2個分數大小相同，意義卻是不同的。

師：請你說一說“”“”“”這3個分數有什么相同點和不同點。

生8：它們的分母不同、分子相同，這說明單位“1”被平均分的份數不同，而它們都表示其中1份。

師：請你再說一說經過對“”“”“”“” “”“”“”的觀察，自己有什么發現。

生8：它們的分母相同、分子不同，這說明單位“1”被平均分成8份，而它們表示的份數不同。

師：下面我們一起走進生活，看一看生活中的分數。1.一節課的時間是小時；2.我們將一節課時間的用在研究分數的意義上。這2個例子中的“”表示的時間相同嗎？為什么？

生9：不相同，因為這2個例子中的單位“1”不同，第1個例子的單位“1”是60分鐘，第2個例子的單位“1”是40分鐘。

通過不同層次的練習，學生在比較中掌握了知識，又發展了靈活運用知識來解決問題的能力。關于2條數軸的練習，有利于學生深化對分數意義的理解，為后續學習分數的基本性質打好基礎。關于分子是“1”的分數和分母是“8”的分數的練習，有利于學生通過比較形成對分母不同的分數和分子不同的分數的感悟。關于時間的練習，有利于學生了解同一個分數在不同場景中所表示的不同意義。

在“分數的意義”這一課的回顧與反思環節，教師在屏幕上展示《莊子》中的“一尺之棰，日取其半，萬世不竭”這句話，之后利用思維導圖，帶領學生回顧這一課學習的知識，鼓勵學生提出自己關于分數的疑問。在聽了學生提出的“為什么還有分子大于分母的分數？”“分母不同的分數該怎樣相加或相減？”“有關分數乘除的題目該怎樣計算？”等疑問后，教師進行了情感教育和數學文化的滲透。回顧與反思是一堂課不可或缺的環節。教師讓學生根據思維導圖內容的變化回顧學習的過程，并讓學生帶著問題開啟接下來的學習之旅，可以在幫助學生整理課堂知識的同時，有效促進學生對知識結構的搭建。

結語

數學知識是數學思想方法的載體，數學思想方法是數學知識的靈魂。對在小學數學學習中具有重要應用價值的數學思想方法進行感悟，是促進數學知識建構的關鍵。通過對數學思想方法的感悟，學生可以理解數學的本質并形成獨特的思維方式。因此，小學數學教師在教學中應注重數學思想方法的滲透，采用多種教學手段來幫助學生掌握數學思想方法；也應注重思維訓練、實踐應用，鼓勵學生自主學習并有效鞏固基礎知識。同時，教師要優化練習內容和反饋方式，及時糾正學生的錯誤，提高學生的解題能力。學生學習數學時，在知識建構中感悟思想方法，能夠用思想方法促進知識建構，從而提升數學核心素養。

【參考文獻】

［1］仲廣群.數學基本思想的內涵、特征及其教學意蘊［J］.江西教育，2012（20/23）：26-27.

［2］林紅霞.感悟“數形結合”的數學思想方法：以《小數的認識》為例［J］.教育研究與評論（小學教育教學），2012（12）：87.

［3］帥莉.抽象概括分數意義 充分體會分數單位：“分數的意義”教學片斷與思考［J］.小學數學教育，2017（14/16）：131-132.