基于模態頻率提升耐久性的拓撲優化方法

摘要：提出一種基于模態頻率提升耐久性能的拓撲優化方法。以動力電池支架為例，依據新設計的動力電池支架的模態頻率和耐疲勞性能的初始仿真結果，以初始模態頻率為設計約束條件，以動力電池支架的尺寸或形貌為設計變量，對其進行拓撲優化，從而為支架的耐久性能提升提供新的設計方案，擺脫了以往依靠經驗進行耐久性能提升的制約。該方法不僅可以更快捷地提升支架的耐久性能，而且也縮短了耐久性能的開發驗證周期并降低了生產成本。

關鍵詞：模態頻率；輕量化；強度分析；疲勞耐久分析；拓撲優化

中圖分類號：U461 收稿日期：2024-07-17

DOI：10.19999/j.cnki.1004-0226.2024.12.007

1 前言

在零件設計初期，為驗證設計零件的耐疲勞性能，一般會采用疲勞軟件對零件的耐疲勞性能進行仿真模擬[1]。仿真模擬結果達到要求后，再對零件進行實際耐久性能測試。采用疲勞分析軟件對零件的耐久性能進行仿真模擬時，如果零件的耐久性能不達標，一般要根據工程師的實際工程經驗對零件進行重新設計，如增加零件的材料厚度、在零件的薄弱處設計加強筋或加強板等，再對設計變更后的零件重新進行耐久性能仿真。這種方式對工程師的工程經驗要求較高，而且零件設計變更后需要進行重復的仿真模擬，仿真模擬過程消耗大量時間，降低了工作效率，且獲得的設計結果也并非最優設計結果。

面對激烈的市場競爭，為縮減開發周期，相關企業迫切需要運用現代先進的設計手段，采用更簡便的方法，在滿足產品性能要求的同時，盡可能降低設計成本。

以往驗證零件的疲勞壽命時，通常先根據零件的疲勞分析結果判斷疲勞斷裂的風險點，然后針對風險點位置，依據經驗對其薄弱環節進行適當加強和改善，隨后再對加強和改善方案重新進行疲勞分析，確定新的方案是否能滿足要求［1］。這種方式通常只考慮了薄弱環節的改善，一方面無法從整個零件的設計角度對零件進行整體改善；另一方面，改善的方案也可能需要經歷多輪次的“設計→驗證→重新設計→再驗證”，設計周期長，對設計師的工程經驗要求較高，且最終得到的設計方案也可能并非最優設計方案。

對此，本文基于模態頻率采用拓撲優化的方法，從零件的整體設計角度出發，可快速為設計師提供設計方案，不僅可提升零件的耐久性能，而且也避免了設計結果需不斷驗證的困擾，縮短零件設計的開發周期，實現產品的快速迭代，并保證設計的零件設計處于最優方案。

2 基于一階模態改善耐久性的拓撲優化流程

拓撲優化是在給定的設計空間尋找最優形狀和材料布局的數據算法[2]。本文采用的優化方法包括自由尺寸優化和形貌優化等。

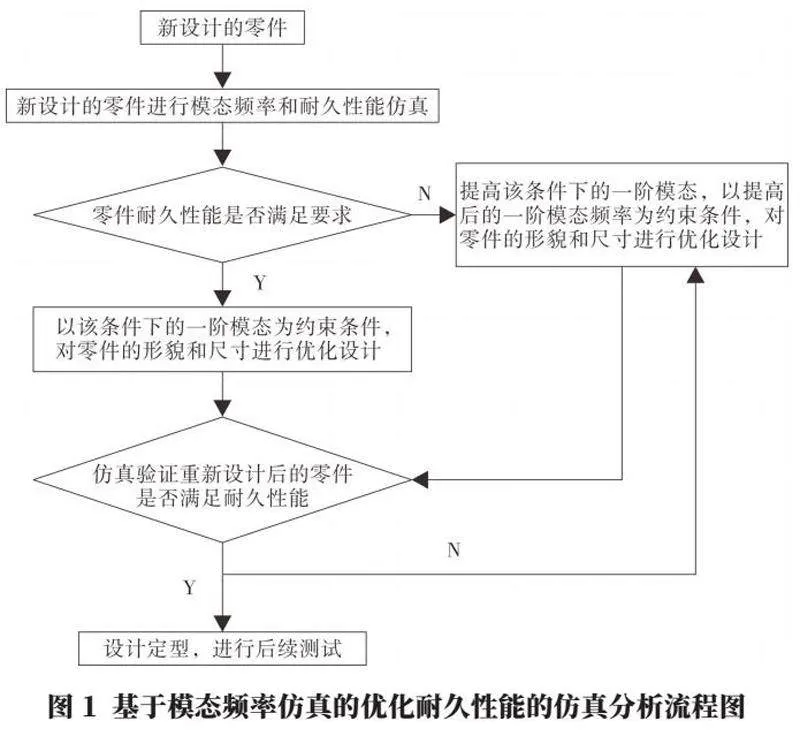
基于一階模態改善耐久性的拓撲優化流程具體如圖1所示。首先，對初始設計的零件進行模態仿真，獲得零件的整體一階模態頻率；然后對零件進行疲勞仿真分析；接著，基于隨機振動理論與頻域疲勞分析方法對新設計的零件進行隨機振動響應分析，結合功率譜密度（PSD），獲得零件的累計損傷值[3-4]。

步驟1：首先判斷初始設計的零件累計損傷值是否大于1.0。如果≥1.0，即新設計的零件耐久性能未滿足要求，則進入步驟2；如果<1.0，即初始設計的零件耐久性滿足要求，則進入步驟3。

步驟2：增加零件當前的整體一階模態頻率值作為一階模態目標值，以一階模態目標值為約束條件，零件的形貌和尺寸為設計變量，零件的質量最小為優化目標，進行拓撲優化；根據優化結果更新零件的形貌和尺寸，再次進行疲勞仿真分析；隨后進入步驟4，判斷更新后的零件是否滿足耐久性要求。

步驟3：以零件當前的整體一階模態頻率值為約束條件，零件的形貌和尺寸為設計變量，零件的質量最小為優化目標，進行拓撲優化；根據優化結果更新零件的形貌和尺寸，再次進行疲勞仿真分析；隨后進入步驟S4，判斷更新后的零件是否滿足耐久性要求。

步驟4：如果更新后的零件不滿足耐久性要求，則按照步驟2，繼續提升一階模態目標值，直至零件的耐久性滿足要求；如果更新后的零件滿足耐久性要求，但零件的耐久性存在較多富余，則按照步驟2，適當降低一階模態目標值，直至零件的耐久性滿足要求，且具有合適的富余量；如果更新后的零件滿足耐久性要求，且零件的耐久性具有合適的富余量，則零件可初步定型，進行后續測試。

3 零件的尺寸拓撲優化

3.1 有限元模型建立

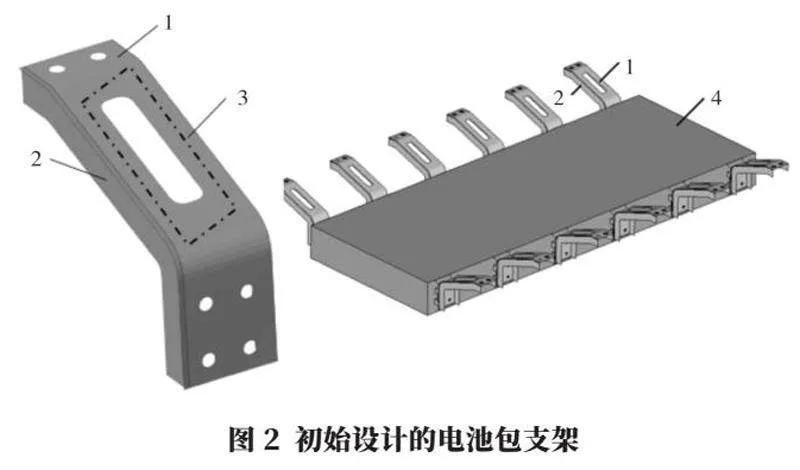
本文以電池包支架為例介紹本方法的使用流程。采用Hyperworks軟件建立電池包和支架的仿真分析模型，圖2為初始設計的電池包支架和搭建的電池包分析模型，其中電池包支架的腹板1厚度為3 mm，電池包支架的加強筋2厚度為3 mm，腹板1上的平面區域3有鏤空部分用于減重，電池包支架全部采用DL510材料，該材料的屈服強度350 MPa，抗拉強度500 MPa。電池包支架為鈑金件，采用殼（shell）單元進行網格劃分，單元尺寸為5 mm。電池包4總質量為500 kg，為提高仿真分析效率，對電池包的模型進行簡化處理，電池包本體采用實體單元模擬。電池包支架的一端與電池包通過螺栓方式進行連接，電池包支架另一端與車架通過螺栓連接［5］。因此，電池包支架與電池包采用Bolt的連接方式，電池包支架與車架連接的螺栓孔進行6個自由度的約束。

3.2 計算初始設計零件的模態和疲勞損傷值

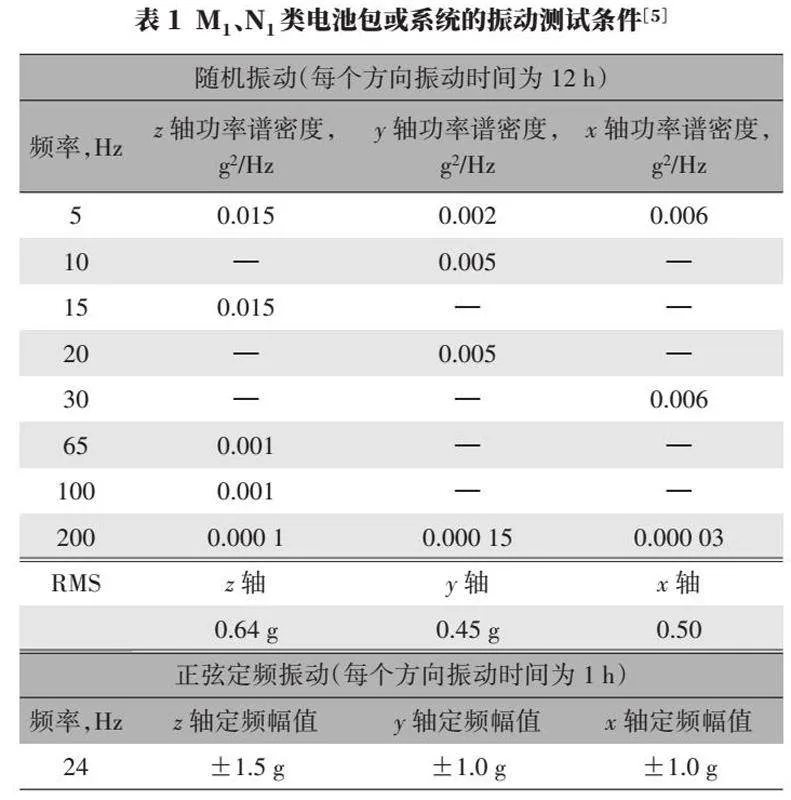
對搭建的電池包模型進行模態仿真，得到該模型的前三階模態頻率分別為38.5 Hz、49.0 Hz和51.6 Hz。然后采用國標GB/T 31467.3—2015《電動汽車用鋰離子動力蓄電池包和系統》給出的電池包振動條件（表1），對電池包支架的疲勞進行仿真分析。本文采用頻域分析方法針對零件的疲勞壽命，利用Ncode疲勞分析軟件計算零件的疲勞壽命。

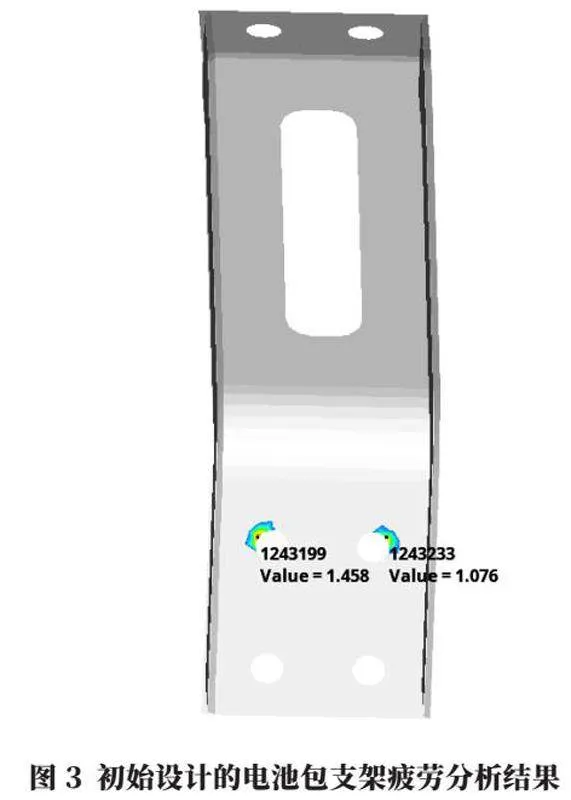
根據電池包支架的疲勞仿真分析結果見圖3，電池包支架上的累計損傷最大值為1.458。因此，需要對電池包支架做進一步設計優化。

3.3 零件的拓撲優化分析

初始設計的電池包支架一階模態為38.5 Hz，在此基礎上將電池包支架的一階模態提升5 Hz，即一階模態目標值設定為43.5 Hz。以43.5 Hz為約束條件，電池包支架的腹板1和加強筋2為設計變量，電池包支架質量最小為優化目標，對圖3搭建的電池包和電池包支架的分析模型進行尺寸拓撲優化。其中，設計變量腹板1的厚度變化范圍為2～4 mm，加強筋2的厚度變化范圍為2～4 mm。圖4所示為電池包支架尺寸拓撲優化結果，根據拓撲優化結果可知，腹板1的厚度為3.6 mm，加強筋2的厚度為2.5 mm時，電池包支架的一階模態可達43.5 Hz，且電池包支架的質量最小。

3.4 優化方案驗證

實際生產過程中，3～4 mm厚度范圍的板材尺寸厚度只有3.0 mm、3.2 mm、3.5 mm、3.8 mm和4.0 mm，為避免后續對板材厚度進行重新加工，同時優先保證耐久性能滿足要求，先將模型中腹板1和加強筋2的厚度分別設定為3.5 mm和2.5 mm，然后重新對圖3的分析模型進行模態仿真和疲勞仿真分析。

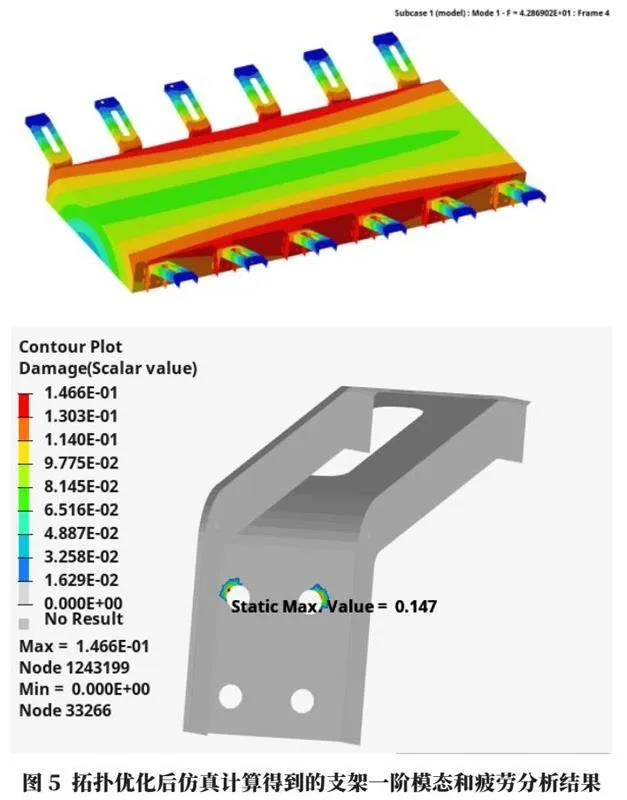
支架的厚度更新后，計算得到的前三階模態分別為42.9 Hz、52.2 Hz和54.3 Hz，符合預計提升的模態要求。隨后，針對拓撲優化后的電池包支架重新進行疲勞分析，電池包支架的最大累計損傷值為0.09，滿足目標要求。圖5所示為拓撲優化后仿真計算得到的支架一階模態和疲勞分析結果。

優化后的電池包支架，最大累計損傷值為0.147，相比初始設計的電池包支架，累計損傷值大幅降低，拓撲優化后的支架耐久性能得到較大提升，滿足使用目標要求。

3.5 優化方案進一步改進

初次結構優化后獲得的最大累計損傷值只有0.147，具備較多的設計余量，因此可進一步對支架進行結構優化。模態頻率的提升有助于改善耐久性能，相當于模態頻率與耐久性能之間是一種連續函數關系。為快速獲取模態頻率對應的期望耐久性能，本文基于連續函數的中值定理，采用二分法取值，對模態目標值的提升幅度進行調整。在本文案例中，將電池包支架的一階模態目標值提升2.5 Hz，即一階模態目標值設定為41.0 Hz。采用上述相同的優化方法，以41.0 Hz為約束條件，電池包支架的腹板1和加強筋2為設計變量，電池包支架質量最小為優化目標，進行電池包支架的尺寸優化。圖6所示為電池包支架進一步拓撲優化結果，其中腹板1的厚度為3.4 mm，加強筋2的厚度為2.6 mm。據此，根據實際生產的現有板材厚度，將腹板1的厚度設定為3.2 mm，加強筋2的厚度設定為2.5 mm。

支架的厚度做進一步更新后，計算得到的前三階模態分別為39.4 Hz、49.6 Hz和51.9 Hz。相比初始設計的支架一階模態，模態值有所提升，可采用該方案進行支架的耐久性仿真驗證。

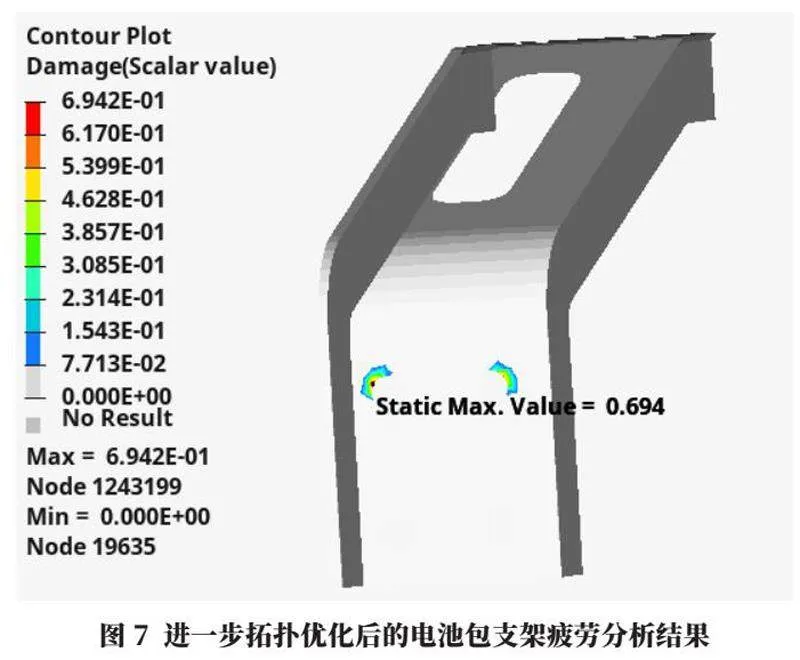
圖7所示為進一步拓撲優化后的電池包支架疲勞分析結果，最大累計損傷值為0.694，滿足目標要求。不僅滿足使用目標要求，而且預留的設計余量富余度也較合理，可作為設計階段的定型樣件。

4 零件的形貌拓撲優化

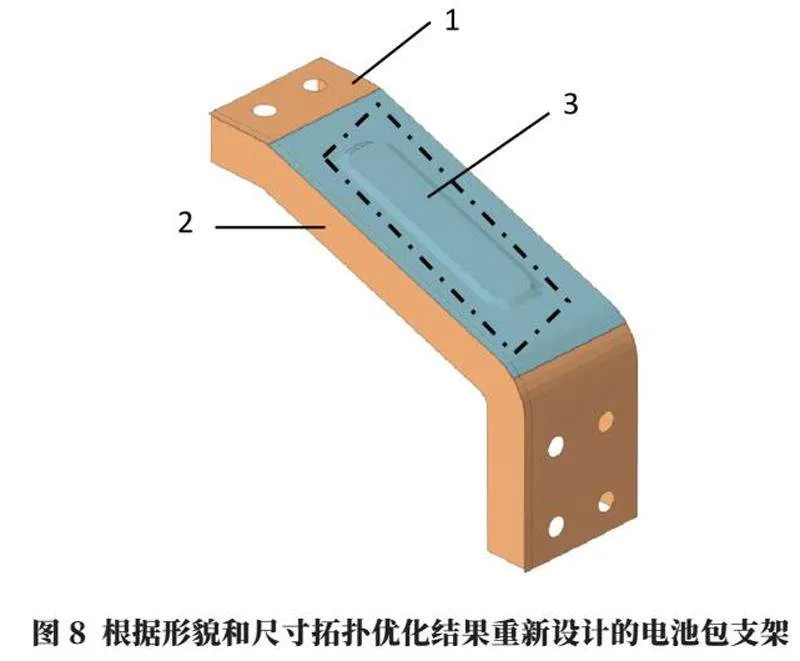
針對電池包支架的優化方法，上文采用了尺寸拓撲優化的方式，本節采用借助形貌拓撲優化方法對電池包支架進行優化設計，以進一步說明本方法的使用效果。與節3中的方法類似，根據形貌和尺寸拓撲優化的結果，電池包支架更新后的形狀如圖8所示。其中，腹板1的厚度為3.2 mm，加強筋2的厚度為3 mm，起筋區域3的起筋高度為3 mm。針對更新后的電池包支架，計算得到的前三階模態分別為40.8 Hz、52.4 Hz和55.5 Hz。針對該電池包支架，根據疲勞分析結果，最大累計損傷值為0.510，滿足目標要求，且預留的設計余量富余度也較合理，也可作為設計階段的定型樣件。

5 結語

a.基于模態頻率的提升，可有效改善零件的耐久性能。

b.以模態頻率為約束條件，以零件的形貌和尺寸為設計變量，以質量最小為優化目標，通過拓撲優化方法，不僅可快速幫助設計師獲得滿足耐久性要求的零件設計方案，減少對設計師的工程經驗依賴，而且還能節省疲勞仿真的驗證次數，節省仿真分析時間，并使最終滿足要求的零件設計方案具有更低的生產成本。

c.對車身的零件設計而言，同類型的零件所處的使用環境不會發生太大變化，因而疲勞分析所用的振動條件大體相同。采用本方法對某個零件進行疲勞壽命分析后，在獲得期望的疲勞壽命時，也相應獲得了該零件對應的模態頻率值。后續新車型的初始設計階段，可初步認為該類型零件的一階模態頻率達到此模態頻率值時，即可滿足疲勞壽命要求。因此，在新車型的初始設計階段，可采用此模態頻率值作為同類型零件的設計參考值，幫助設計師更好地完成初始階段的零件設計。通過對不同零件的模態頻率值的積累，也可為新車型的整體開發設計提供更多參考和依據。

參考文獻：

[1]劉龍濤，李傳日，程祺，等.某型機載模塊的隨機振動疲勞分析[J].機械強度，2019（41）：66-71.

[2]方獻軍，徐自立，熊春明.OptiStruct及HyperStudy優化與工程應用[M].北京：機械工業出版社，2021.

[3]戴紅梁，熊飛，劉靜，等.基于某車型動力電池包的隨機振動疲勞分析與結構設計改進[J].機械強度，2021，43（3）：1266-1270.

[4]孟彩茹，盧博友.基于PSD的隨機載荷下振動疲勞壽命估算[J].機械設計，2009，26（5）：73-75.

[5]GB/T 31467.3—2015 電動汽車用鋰離子動力蓄電池包和系統第3部分：安全性要求與測試方法[S].

作者簡介：

張曉宇，男，1989年生，工程師，研究方向為整車結構仿真分析。