“數形結合”巧解二次函數問題

【摘要】二次函數是初中數學教材中難度比較高的知識點,相對艱深晦澀,可能會給很多學生帶來學習障礙.想要解決二次函數問題不能依靠生搬硬套定義和公式,而是需要巧借“數形結合”的理念,利用函數圖象反映數學問題中的各個參數和條件,找到解題的入手點.本文將從基礎訓練、拓展提升、拔高練習的層面介紹用“數形結合”思想解決“二次函數y=ax2的圖象和性質”相關數學問題的方法,以供參考.
【關鍵詞】數形結合;二次函數問題;初中數學
1 “數形結合”巧解二次函數問題——“二次函數y=ax2的圖象和性質”
1.1 基礎訓練
(1)課前預習測試
教師要求學生提前預習教材內容,結合課內外資源完成“預習反饋”任務卡.
函數y=x2的圖象開口,對稱軸為,頂點是;在對稱軸的左側,y隨x的增大而,在對稱軸的右側,y隨x的增大而.
函數y=-x2的圖象開口,對稱軸為,頂點是;在對稱軸的左側,y隨x的增大而,在對稱軸的右側,y隨x的增大而.
教師要求學生綜合教材給出的知識點及“預習反饋”任務卡填寫內容,嘗試畫出二次函數y=x2的圖象.學生在教師的指導下按照“列表→描點→連線”完成了這一任務,見表1.
y=x2的函數圖象如下:
1.2 拓展提升——y=( k-1)x2的函數圖象
問題1 要求學生在掌握y=ax2函數圖象繪制方法的基礎上,嘗試畫出y=-ax2(a>0)的圖象,并且探究兩個函數圖象之間的關系.
根據圖2給出的函數圖象,學生可以總結出“這兩個二次函數的二次項系數互為相反數,開口方向相反,開口大小相同,關于x軸對稱”.
問題2 嘗試畫出二次函數y=-12x2,y=-x2,?偆ay=-2x2的函數圖象,觀察三個函數圖象的開口大小及其與a的大小之間的關系.
學生觀察圖象后發現:對于拋物線 y=ax2 ,當a<0時,a越小,開口越小,即|a|越大,拋物線的開口越小.
問題3 觀察函數y=( k-1)x2的圖象(如圖4),求k的取值范圍.
通過觀察函數圖象可以看出,該函數開口向上,則k-1>0,即k>1.
1.3 拔高練習
經過基礎訓練和拓展提升環節的練習,學生已經基本掌握了二次函數y=ax2函數圖象的畫法和性質,也可以解決一些相關的基礎問題.
問題1 如圖5,直線y=3x+4與拋物線y=x2交于A、B兩點,求出A、B兩點的坐標以及兩交點與原點所圍成的三角形的面積.
由題意得y=3x+4y=x2,
解得x=4y=16或x=-1y=1,
通過計算可得兩函數的交點坐標為A(4,16)和B(-1,1).
因為直線y=3x+4與y軸相交于點C(0,4),即CO=4,
所以S△ACO=12×4×4=8,S△BOC=12×4×1=2,
所以S△ABO=S△ACO+S△BOC=10.
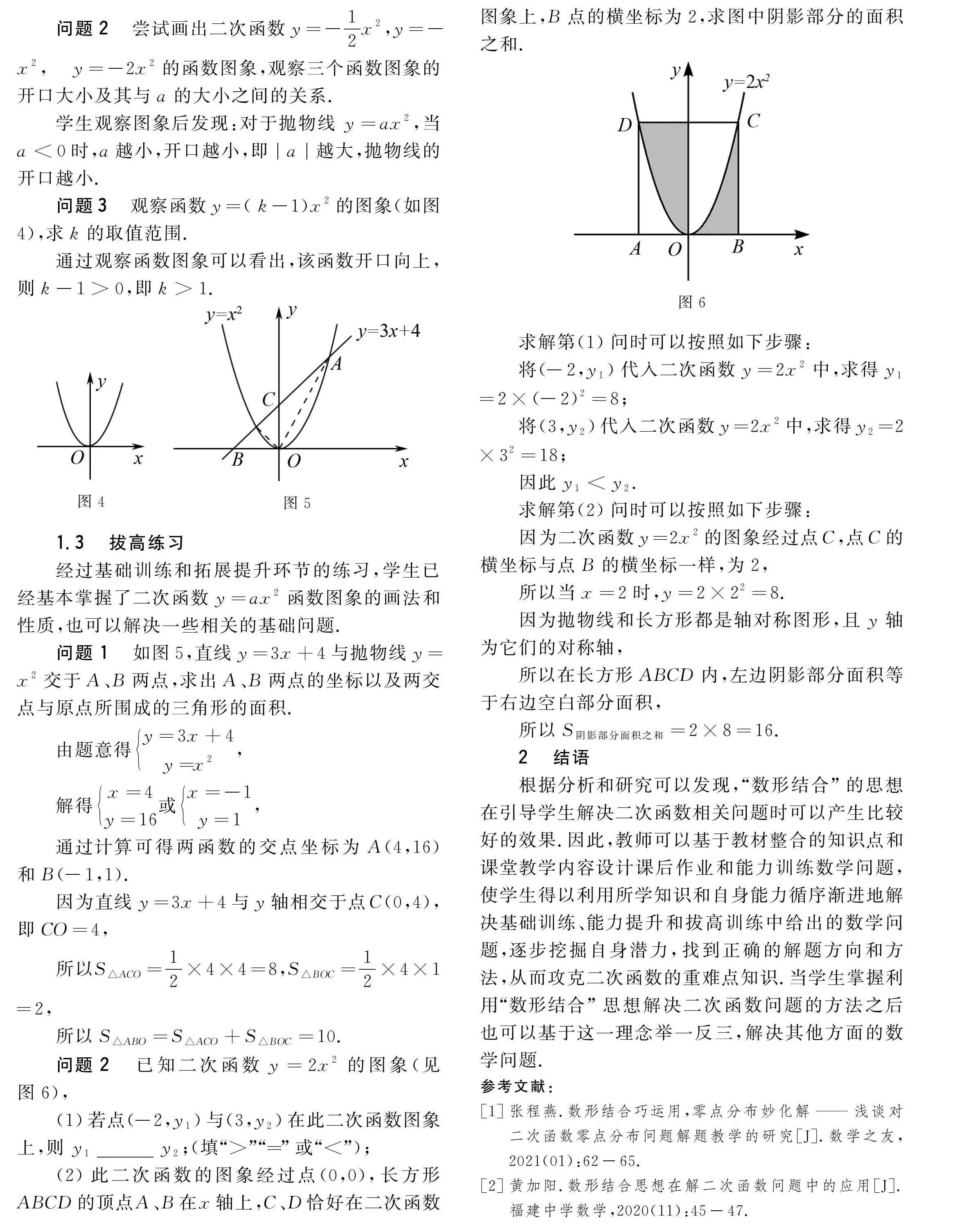
問題2 已知二次函數y=2x2的圖象(見圖6),
(1)若點(-2,y1)與(3,y2)在此二次函數圖象上,則 y1 y2;(填“>”“=”或“<”);
(2)此二次函數的圖象經過點(0,0),長方形ABCD的頂點A、B在x軸上,C、D恰好在二次函數圖象上,B點的橫坐標為2,求圖中陰影部分的面積之和.
求解第(1)問時可以按照如下步驟:
將(-2,y1)代入二次函數y=2x2中,求得y1=2×(-2)2=8;
將(3,y2)代入二次函數y=2x2中,求得y2=2×32=18;
因此y1<y2.
求解第(2)問時可以按照如下步驟:
因為二次函數y=2x2的圖象經過點C,點C的橫坐標與點B的橫坐標一樣,為2,
所以當x=2時,y=2×22=8.
因為拋物線和長方形都是軸對稱圖形,且y軸為它們的對稱軸,
所以在長方形ABCD內,左邊陰影部分面積等于右邊空白部分面積,
所以S陰影部分面積之和=2×8=16.
2 結語
根據分析和研究可以發現,“數形結合”的思想在引導學生解決二次函數相關問題時可以產生比較好的效果.因此,教師可以基于教材整合的知識點和課堂教學內容設計課后作業和能力訓練數學問題,使學生得以利用所學知識和自身能力循序漸進地解決基礎訓練、能力提升和拔高訓練中給出的數學問題,逐步挖掘自身潛力,找到正確的解題方向和方法,從而攻克二次函數的重難點知識.當學生掌握利用“數形結合”思想解決二次函數問題的方法之后也可以基于這一理念舉一反三,解決其他方面的數學問題.
參考文獻:
[1]張程燕.數形結合巧運用,零點分布妙化解——淺談對二次函數零點分布問題解題教學的研究[J].數學之友,2021(01):62-65.
[2]黃加陽.數形結合思想在解二次函數問題中的應用[J].福建中學數學,2020(11):45-47.

