基于擴展卡爾曼濾波的農機路徑跟蹤控制算法研究

摘要：智能農機的路徑跟蹤精度受田地地形、農機結構等多因素的影響，會導致壓壞滴灌帶等嚴重后果。以棉花播種機為研究對象，提出一種由Stanley跟蹤算法和線性二次最優控制（LQR）算法組成的切換式跟蹤算法，引導農機快速入線和保持直線精度；另外為消除靜態橫向誤差，加入針對航向角誤差的擴展卡爾曼濾波器（EKF）。仿真結果顯示，切換式跟蹤算法在進入目標直線后可有效消除靜態橫向誤差。實車試驗結果表明，當給定初始橫向誤差為0.5 m，速度為3.6 km/h時，入線時間為6.88 s，超調量為0.041 m；當給定初始橫向誤差為0 m，速度為3.6 km/h時，直線跟蹤精度控制在±0.025 m范圍內，滿足實際農機高精度的直線作業要求，表明該算法具有良好的跟蹤精度和抗干擾能力，有利于提升農業生產效率。

關鍵詞：智能農機；定位技術；擴展卡爾曼濾波；路徑跟蹤；自動駕駛

中圖分類號：S220

文獻標識碼：A

文章編號：20955553 （2024） 070215 07

Research on path tracking control algorithm of agricultural machinery

based on extended Kalman filter

Qian Junnan， Feng Sang， Li Hang， Zhang Yong

（School of Mechanical and Electrical Engineering， Guangdong University of Technology， Guangzhou， 510006， China）

Abstract：

The path tracking accuracy of intelligent agricultural machinery is affected by many factors such as field terrain and machinery structure， which may lead to serious consequences such as crushing the drip irrigation belt. In this paper， taking the cotton planter as the research object， a switching tracking algorithm consisting of Stanley tracking algorithm and linear quadratic optimal control （LQR） algorithm is proposed to guide the agricultural machine to enter the line quickly and maintain the straight line accuracy. In addition， in order to eliminate the static lateral error， an extended Kalman filter （EKF） for heading angle error is added. The simulation results show that the switching tracking algorithm can eliminate the static lateral error after entering the straight target line. The real vehicle test results show that when the given initial lateral error is 0.5 m and the speed is 3.6 km/h， the entry time is 6.88 s， and the overshoot is 0.041 m. When the given initial lateral error is 0 m， and the speed is 3.6 km/h， the straight-line tracking accuracy is controlled within ±0.025 m， which meets the requirements of high-precision straight-line operation of actual agricultural machinery. It shows that the algorithm studied has good tracking accuracy and anti-interference ability and it is conducive to improving agricultural production efficiency.

Keywords：

intelligent agricultural machinery; positioning technology; extended Kalman filter; path tracking; automatic driving

0 引言

隨著“智慧農業”的推行，農機自動導航技術逐漸成為智能化精準農業中的重要組成部分［13］。路徑跟蹤控制器的作用是使得農機能夠跟隨既定目標路徑［4］，其性能優劣將直接影響農機能否正確完成給定的駕駛任務。目前國內外學者都對農機自動駕駛路徑跟蹤方面展開廣泛的研究。

在國外，Alipour等［5］提出一種基于滑模控制規則的輪式移動機器人系統的軌跡追蹤控制器。Khalaji［6］提出一種基于轉矩計算的PID控制器，用于拖拉機—掛車輪式機器人的軌跡跟蹤。Han等［7］提出一種能適應不同地面附著特性的基于滑動估計的農機路徑跟蹤算法。Murillo等［8］提出了一種具有雙轉向機構的鉸接式拖拉機數學模型，能夠用與小型土地的靈活作業。Nehme等［9］提出了基于激光雷達的魯棒結構跟蹤方法，適合葡萄園等復雜場景，降低導航成本。在國內，Xu等［10］提出了基于4WS農機高效MPC控制器，兼顧了效率與精度。Zhou等［11］提出全球定位系統（GPS）受擾環境中，拖拉機—掛車系統的一般路徑跟蹤框架。武濤等［12］設計了一種快速終端滑模跟蹤控制算法，有效抑制振動帶來的干擾。張智剛等［13］開發了一套基于星基增強精密單點定位的農機自動導航系統。張培培等［14］采用滑模控制，對拖拉機和牽引式農具進行路徑跟蹤。

為提高農業生產效率，避免自動駕駛農機偏離目標路徑壓壞滴灌帶而造成損失，本文以棉花播種機為試驗平臺，提出一種切換式跟蹤控制算法，采用Stanley算法引導農機快速入線，入線后采用LQR算法保持直線精度；采用基于航向誤差的EKF濾波器消除定位系統安裝帶來的靜態橫向誤差并進行試驗驗證。

1 路徑跟蹤策略

1.1 LQR控制器

1.1.1 運動學模型

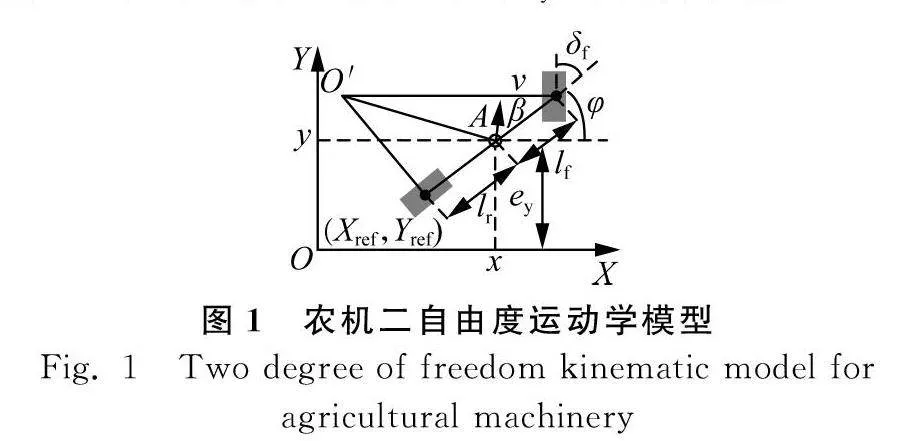
農機在農田工作時處于低速狀態，受輪胎側偏影響小，可以采用車輛二自由度運動學模型［15］來近似描述，如圖1所示。OXY為慣性坐標系；X和Y為橫縱坐標；X·為農機在橫坐標方向上的速度，m/s；Y·為農機在縱坐標方向的速度，m/s；A點是質心；O′點為車輛的瞬時轉動中心；lf和lr分別為控制點與前后軸的距離，m；δf為前輪轉角，rad；β為質心側偏角；φ為航向角，rad；v為行駛速度，m/s；ey為橫向誤差，m。

根據幾何運動關系可以得到農機運動學模型

X·=vcos（φ+β）

Y·=vsin（φ+β）

φ·=vsin βlr

（1）

其中，β=tan-1lrLtanδf，則

Y·=vφ+tan-1lrLtanδf

（2）

φ·=vLtanδf

（3）

式中：

L——農機的軸距，m。

1.1.2 軌跡跟蹤誤差模型

為計算簡便，設定Y=0為目標直線。跟蹤過程主要存在車輛質心到目標路徑的橫向偏差ey和車輛方向與路徑方向的航向偏差eφ。描述ey和eφ有

ey=-Xsinφref+Ycosφref

（4）

eφ=φ-φref

（5）

式中：

φref——參考路徑的方位角，rad。

前輪轉角通過方向盤電機控制，采用PD控制有

δf=uf·PPD·Kpτs2+（1+KpDPD）s+PPD

（6）

式中：

uf——期望車輪轉角，rad；

PPD——比例系數；

s——拉普拉斯變換域中的頻率；

DPD——微分系數；

τ——時間常數；

Kp——電機轉角與車輪轉角的比例系數。

由式（1）～式（6）推導得軌跡跟蹤誤差模型

e·y=vφ+lrLδf

e·φ=vLδf

δ·f=δ·f

δ··f=-1+KpDPDτδ·f-PPDτδf+PPD·Kpτuf

（7）

將式（7）改寫成狀態空間方程，有

x·=Ax+Buf

（8）

其中，

A=

0vvlr/L0

00vL0

0001

00-KpPPDτ（1+DPDKp）τ

，

B=

000KpPPDτ

。

1.1.3 LQR控制器設計

LQR控制器［16］是一種多目標最優控制。LQR控制的目標函數

J（x）=∑∞t=0xTQx+uTRu

（9）

式中：

J（x）——目標函數；

x——狀態量；

u——控制量；

Q——狀態量加權矩陣；

R——控制量加權矩陣。

其中，Q=

100000

01000

0010

0001

，

R=［500］。

一般全狀態反饋控制器控制律有

u=-Kx

（10）

式中：

K——控制增益系數。

將式（10）代入目標函數有

J（x）=∑∞t=0xT（Q+KTRK）x

（11）

假設存在常量矩陣P使系統趨于穩定，可得

K=（R+BTPB）-1BTPA

（12）

P為Ricatti方程正定解，即

P=-ATPB（R+BTPB）-1BTPA+ATPA+Q

（13）

1.2 Stanley控制器

采用基于幾何學的Stanley控制器［17， 18］，將車輛前軸作為控制參考點，由圖2可得

δf=eφ+arctanKeyv

（14）

1.3 基于航向誤差的擴展卡爾曼濾波器

對系統中RTK-GPS的定位、IMU的姿態信息以及農機的車速傳感器信號數使用擴展卡爾曼濾波（Extended Kalman Filter，EKF）［19， 20］可得估計位置和航向角。

在卡爾曼濾波中，系統的狀態改變和觀測服從

xk=Aexk-1+Beuk-1

ze（k+1）=Cexk

（15）

式中：

xk、xk-1——

當前k時刻和上一時刻的模型狀態變量；

Ae——系統狀態轉移矩陣；

Be——控制輸入矩陣；

Ce——系統輸出矩陣。

在基于航向誤差的擴展卡爾曼濾波器中，以X·、Y·、vb、φ、wb以及φb作為狀態變量；以v、w為控制輸入。航跡推算擴展卡爾曼濾波的連續型表達式為

x·=

X·

Y·

v·b

φ·

w·b

φ·b

=

（v-vb）sin φ

（v-vb）cos φ

vb

w+wb

wb

φb

（16）

式中：

vb——

傳感器測量速度過程產生的零點漂移；

φb、φ·b——

組合導航測量航向角和航向角速度加速過程中傳感器產生的零點漂移；

w——IMU測量的航向角速度，rad/s；

wb、w·b——

IMU測量航向角速度和航向角加速度過程中產生的漂移。

根據前向歐拉法，可得離散化模型為

x（k+1）

=

X（k+1）

Y（k+1）

vb（k+1）

φ（k+1）

wb（k+1）

φb（x+1）

=

X（k）+［v（k）-vb（k）］sin［φ（k）］dt

Y（k）+［v（k）-vb（k）］cos［φ（k）］dt

vb（k）

φ（k）+［w（k）+wb（k）］dt

wb（k）

φb（k）

（17）

根據雅可比矩陣法，Ae和Be矩陣為

Ae=

00-sinφ（v-vb）cosφ00

00-cosφ-（v-vb）sinφ00

000000

0000-10

000000

000000

（18）

Be=

sinφ0

cosφ0

00

00

（19）

系統傳感器包含GPS-RTK與IMU，在狀態觀測中以質心位置和航向角作為觀測值，故ze和Ce矩陣表示為

ze（k+1）=Cex（k）

（20）

式中：

ze——傳感器輸出的測量向量；

Ce——觀測矩陣，Ce=

100000

010000

000101

。

1.4 路徑跟蹤控制器總體設計

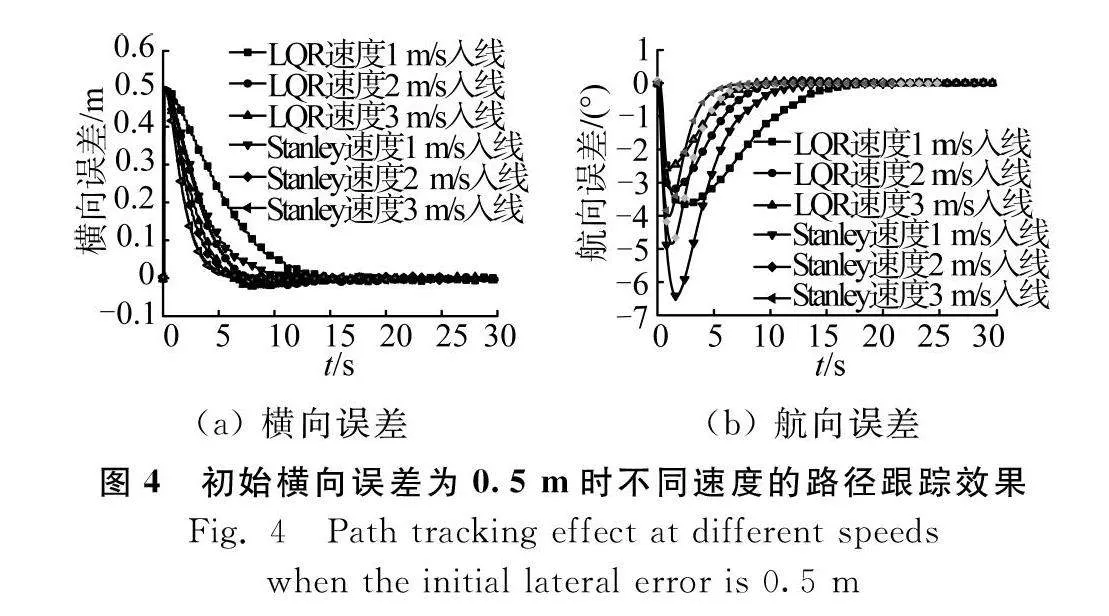
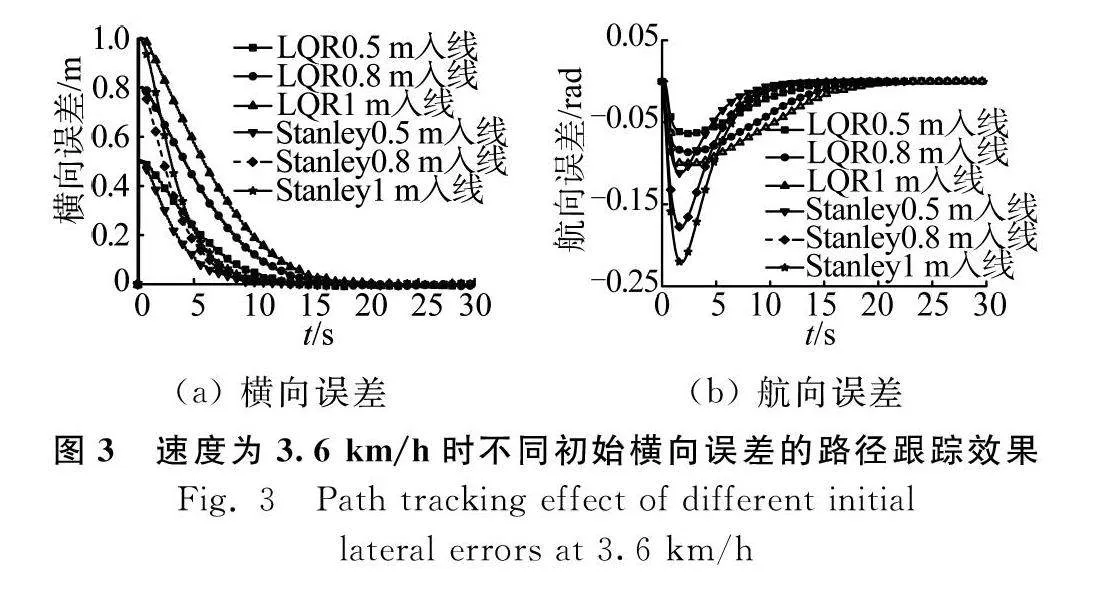
分別以不同初始橫向誤差和不同速度對LQR控制器和Stanley控制器都進行仿真試驗，如圖3和圖4所示。

由圖3可以看出，在不同初始橫向位置，相比LQR控制器，Stanley控制器入線時間減少了7.7～11.1 s，而入線距離減少了7.7～10.3 m，說明Stanley入線效率高。根據圖4可知，隨著速度提高，LQR控制器入線時會發生0.03 m的超調，但是線上精度的均值和標準差均小于0.003 m，相比Stanley控制器的線上控制效果更為出色。

因此選擇將兩種控制器結合，利用Stanley控制器進行入線；在農機入線后，切換為LQR控制器完成直線路徑跟蹤。其中入線判斷標準為橫向誤差絕對值小于0.05 m，航向誤差絕對值小于0.03 rad（1.72°）。

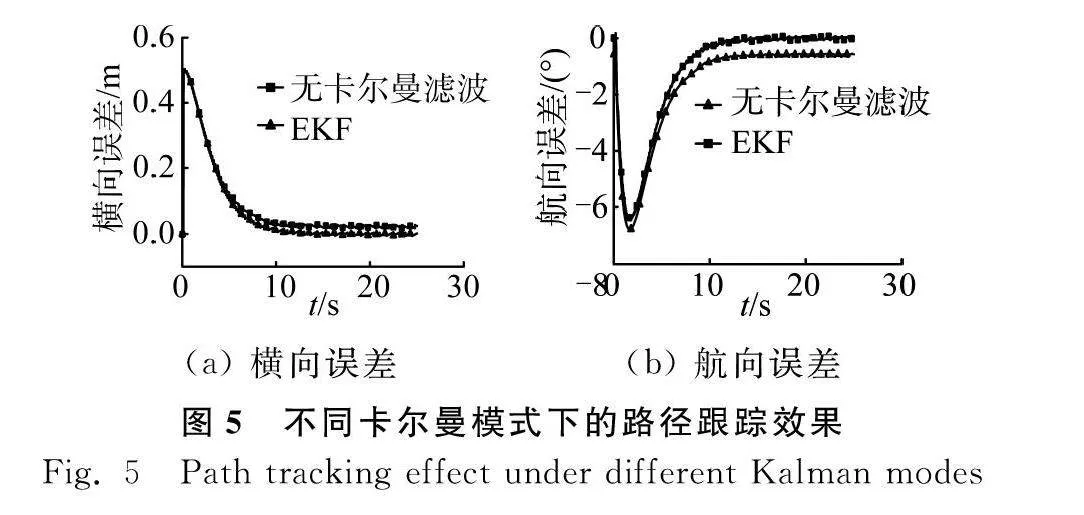
為模擬傳感器誤差的工況，設置固定航向偏移角為0.7°，對速度為3.6 km/h時進行仿真，如圖5所示。

從圖5可以看出，定位系統因存在安裝偏差（即航向誤差為0.7°），入線用時3 s，入線后會導致0.03 m的橫向誤差和0.7°的航向角誤差。引入EKF后，入線用時3.5 s，橫向誤差和航向角誤差均在0附近波動，有效消除了安裝誤差造成的靜態誤差。

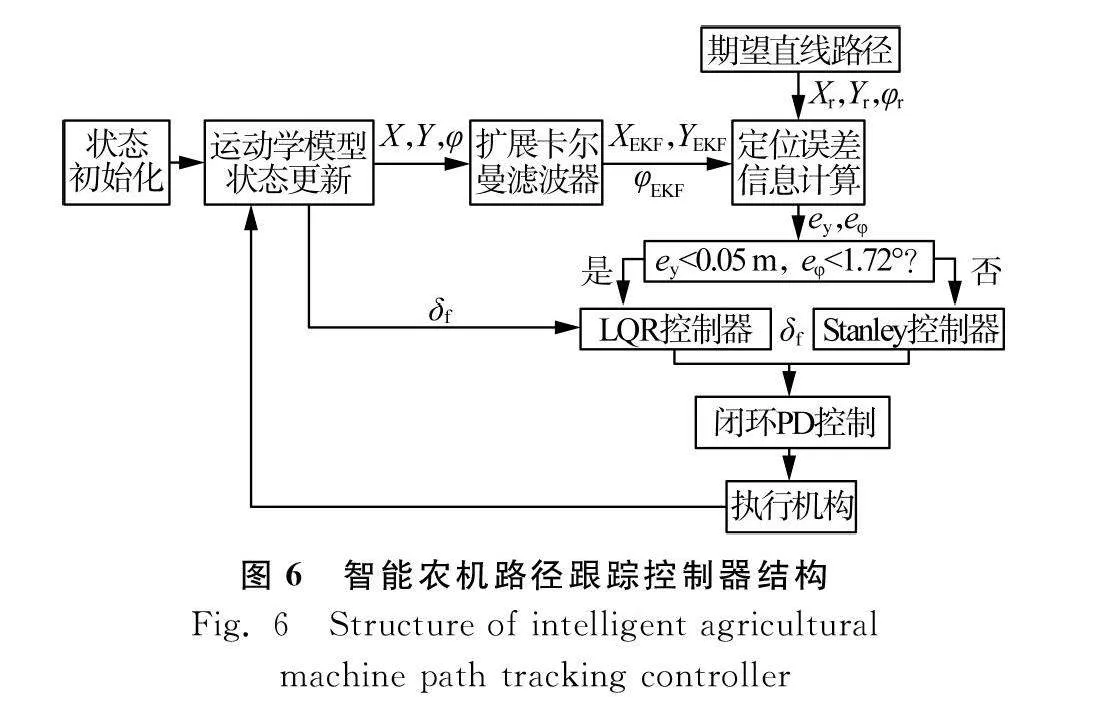
最后根據仿真結果設計如圖6所示的路徑跟蹤控制器。

2 實車試驗

2.1 農機自動駕駛系統試驗平臺及場景

為了避免GPS-RTK雙天線因遮擋而受干擾，將其與集成控制器一同水平安裝于農機頂部。其中GPS-RTK模塊用于獲取農機實時定位信息；IMU模塊中加速度計可以獲取農機實時的速度與加速度信息，陀螺儀用于獲取農機實時的姿態信息；控制器間通過CAN輸出期望電機角度至電機執行機構，實現自動轉向。本文采用的農機參數如表1所示。

農機自動駕駛系統實車試驗平臺組成如圖7所示，該系統主要由約翰迪爾903型農機、集成控制器、電動轉向系統、GPS-RTK雙天線、顯示終端等構成。

為了檢驗自動駕駛系統的可行性，在某棉花種植試驗場地進行試驗。將農機入線時的入線時間、入線距離以及超調量作為自動駕駛系統入線性能的評價指標；把農機的實際行駛路徑相對參考路徑的絕對平均橫向誤差以及其標準差，作為自動駕駛系統跟蹤直線精度的評價指標。

2.2 不同行駛速度下的直線跟蹤試驗

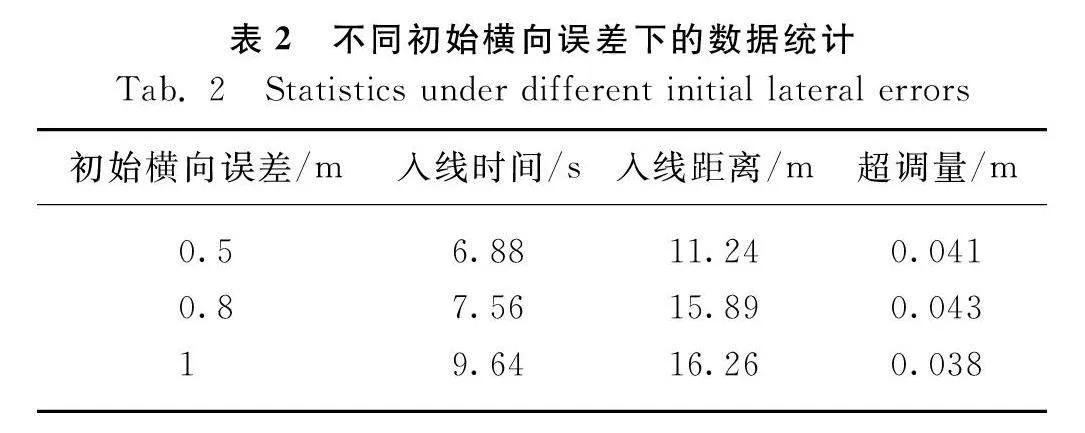
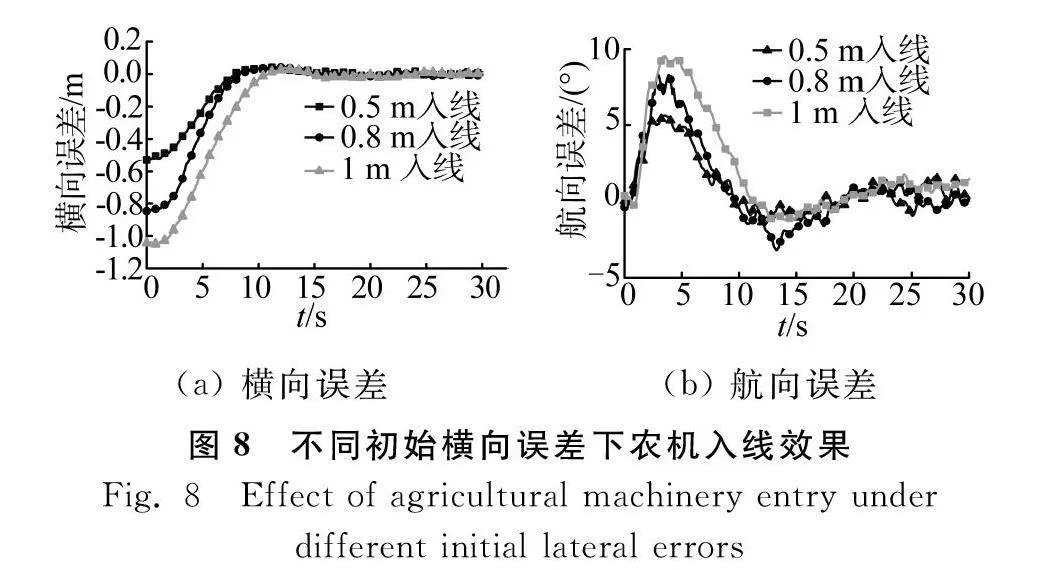
試驗時農機行駛的速度設為3.6 km/h，初始航向誤差為0°，設置農機的初始橫向誤差為0.5 m、0.8 m和1 m。農機在不同初始橫向誤差下的入線效果如圖8所示，表2為不同初始橫向誤差下的入線性能數據。

根據圖8和表2可以看出，農田試驗的結果與仿真試驗結果趨勢相似，但因為農田道路對農機自動駕駛系統的干擾性很大，以及農機轉向系統中液壓偏移的影響導致的響應滯后等各種環境因素，使試驗入線性能效果與仿真入線結果存在差異。

當初始橫向誤差絕對值為0.5 m時，在入線過程出現約0.041 m的超調，在7 s內自動駕駛系統即可控制農機入線，且入線距離為11.24 m。當初始航向誤差絕對值增加至1 m入線時，入線時間增加了約3 s，入線距離增加約5 m，超調量均保持在0.04 m左右。由此可見，隨著初始航向誤差的增加，入線時間以及入線距離逐漸增加。當橫向誤差越大時，航向誤差隨之增加，控制器會輸出較大的期望前輪轉角量，使農機的航向角增大；當接近參考路徑時，逐漸減小前輪轉角，使農機的航向誤差逐漸降低，最后農機逐步跟蹤至直線上。入線過程中有出現超調，但仍可快速收斂至0附近。

2.3 不同行駛速度下的直線跟蹤試驗

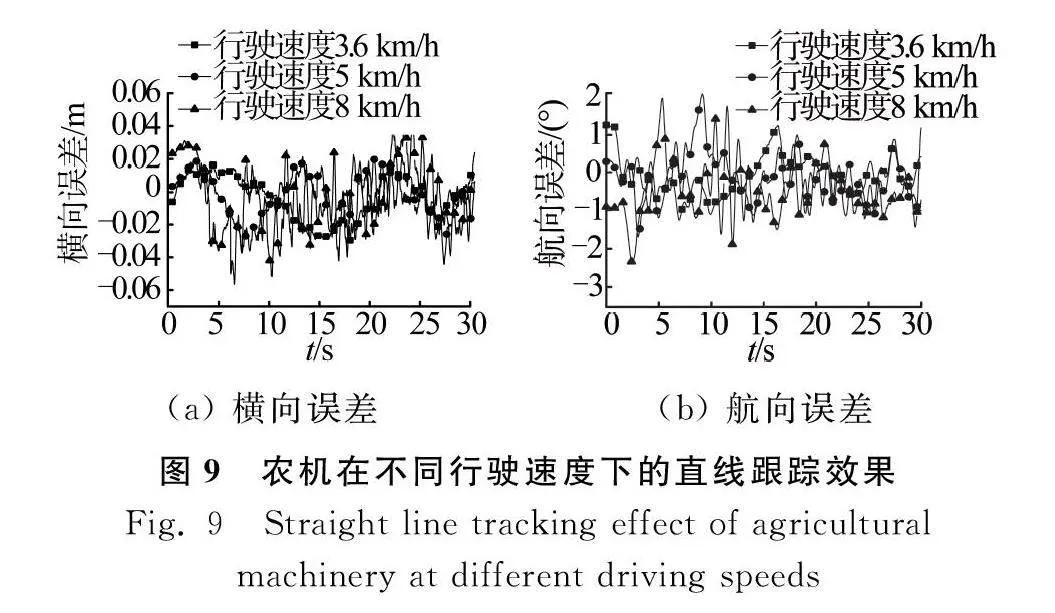
試驗時速度分別為3.6 km/h、5 km/h和8 km/h，初始橫向誤差為0 m。農機在不同行駛速度下的直線跟蹤效果如圖9所示，包括橫向誤差及航向誤差。表3為不同行駛速度下的直線跟蹤性能數據統計。

根據圖9和表3可以看出，實際農機作業環境中存在著許多的干擾因素，對農機自動駕駛系統的影響很大。當初始橫向誤差絕對值為0 m、農機以3.6 km/h速度行駛時，橫向誤差的絕對值均值為0.012 m，標準差為0.015 m，實際可以控制農機保持在橫向誤差約為±0.025 m的范圍附近波動；當以8 km/h速度行駛時，橫向誤差的絕對值均值增加了0.011 m，橫向誤差最大值增加了0.033m，農機保持在距離參考路徑±0.06 m的范圍內波動，并且航向誤差的波動范圍也有所增加。隨著速度升高時，橫向誤差的絕對值均值和標準差隨之增加，這是因為農機在顛簸路段以較高速行駛時，自身的振動也更加大，容易出現滑移。此外，當農機走過顛簸農田道路時，因行駛速度較大時，使轉向執行機構對輸出的前輪轉角響應滯后，導致地形因素對農機自動駕駛系統的干擾有放大作用。

3 結論

1）" 本文采用Stanley算法和四階LQR算法組成的切換式控制算法實現智能農機的跟蹤控制，可以保證智能農機能夠在跟蹤指定直線時能夠迅速入線和直線跟蹤保持高精度；同時加入基于EKF的航向濾波器，能夠減少定位傳感器帶來的誤差。

2）" 在仿真環境中，分別設置3組試驗，在不同初始橫向誤差中，Stanley控制器與LQR控制器相比，入線時間減少76%，而入線距離減少57%；在不同速度下直線跟蹤，LQR的橫向位置誤差仍保持在0.003 m，而Stanley的橫向誤差隨著速度增大從0.04 m增加到0.08 m，說明LQR控制器受速度變化影響較小，魯棒性較好；結合兩者優點，設計Stanley和LQR組成的切換式控制器。仿真試驗結果表明，當假設存在安裝誤差，無EKF的切換式控制器無法消除靜態橫向誤差和航向角誤差；而采用EKF則可有效消除這些靜態誤差，且橫向標準差僅為0.01 m。

3）" 以約翰迪爾903型農機為試驗平臺，并搭載集成控制器、GPS-RTK雙天線等設備，在棉花種植場地進行自動駕駛作業試驗。試驗結果表明，當初始橫向誤差為0.5 m、速度為3.6 km/h時，入線時間為6.88 s，入線距離為11.24 m，超調量為0.041 m，直線跟蹤精度控制在±0.025 m范圍內，滿足實際農機高精度的直線作業要求。

參 考 文 獻

［1］張漫， 季宇寒， 李世超， 等. 農業機械導航技術研究進展［J］. 農業機械學報， 2020， 51（4）： 1-18.

Zhang Man， Ji Yuhan， Li Shichao， et al. Research progress of agricultural machinery navigation technology ［J］. Transactions of the Chinese Society for Agricultural Machinery， 2020， 51（4）： 1-18.

［2］王輝， 王桂民， 羅錫文， 等. 基于預瞄追蹤模型的農機導航路徑跟蹤控制方法［J］. 農業工程學報， 2019， 35（4）： 11-19.

Wang Hui， Wang Guimin， Luo Xiwen， et al. Path tracking control method of agricultural machine navigation based on aiming pursuit model ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2019， 35（4）： 11-19.

［3］徐廣飛， 陳美舟， 金誠謙， 等. 拖拉機自動駕駛關鍵技術綜述［J］. 中國農機化學報， 2022， 43（6）： 126-134.

Xu Guangfei， Chen Meizhou， Jin Chengqian， et al. A review of key technology of tractor automatic driving ［J］. Journal of Chinese Agricultural Mechanization， 2022， 43（6）： 126-134.

［4］嚴國軍， 賁能軍， 顧建華， 等. 基于MPC的無人駕駛拖拉機軌跡跟蹤控制［J］. 重慶交通大學學報（自然科學版）， 2019， 38（9）： 1-6.

Yan Guojun， Ben Nengjun， Gu Jianhua， et al. Trajectory tracking control of intelligent tractor based on MPC algorithm ［J］. Journal of Chongqing Jiaotong University of Technology （Natural Science）， 2019， 38（9）： 1-6.

［5］Alipour K， Robat A B，Tarvirdizadeh B. Dynamics modeling and sliding mode control of tractor-trailer wheeled mobile robots subject to wheels slip ［J］. Mechanism and Machine Theory， 2019， 138： 16-37.

［6］Khalaji A K. Pid-based target tracking control of a tractor-trailer mobile robot ［J］. Proceedings of the Institution of Mechanical Engineers， Part C. Journal of Mechanical Engineering Science， 2019， 233（13）： 4776-4787.

［7］Han X， Kim H J， Jeon C W， et al. Application of a 3D tractor-driving simulator for slip estimation-based path-tracking control of auto-guided tillage operation ［J］. Biosystems Engineering， 2019， 178： 70-85.

［8］Murillo M， Sanchez G， Deniz N， et al. Improving path-tracking performance of an articulated tractor-trailer system using a non-linear kinematic model ［J］. Computers and Electronics in Agriculture， 2022， 196： 106826.

［9］Nehme H， Aubry C， Solatges T， et al. Lidar-based structure tracking for agricultural robots： Application to autonomous navigation in vineyards ［J］. Journal of Intelligent amp; Robotic Systems， 2021， 103（4）： 61.

［10］Xu J， Lai J， Guo R， et al. Efficiency-oriented MPC algorithm for path tracking in autonomous agricultural machinery ［J］. Agronomy， 2022， 12（7）： 1662.

［11］Zhou S， Zhao H， Chen W， et al. Robust path following of the tractor-trailers system in GPS-denied environments ［J］. IEEE Robotics and Automation Letters， 2019， 5（2）： 500-507.

［12］武濤， 李彥明， 林洪振， 等. 基于干擾觀測器的直播機路徑跟蹤快速終端滑模控制［J］. 農業機械學報， 2021， 52（12）： 24-31.

Wu Tao， Li Yanming， Lin Hongzhen， et al. Fast terminal sliding mode control for autonomous rice seeding machine based on disturbance observer ［J］. Transactions of the Chinese Society for Agricultural Machinery， 2021， 52（12）： 24-31.

［13］張智剛， 王明昌， 毛振強， 等. 基于星基增強精密單點定位的農機自動導航系統開發與測試［J］. 華南農業大學學報， 2021， 42（6）： 109-116.

Zhang Zhigang， Wang Mingchang， Mao Zhenqiang， et al. Development and test of auto-navigation system for agricultural machinery based on satellite based precision single-point positioning ［J］. Journal of South China Agricultural University， 2021， 42（6）： 109-116.

［14］張培培， 楊自棟， 趙相君. 拖拉機—牽引式農機具的運動建模與跟蹤控制［J］. 中國農機化學報， 2021， 42（4）： 128-133.

Zhang Peipei， Yang Zidong， Zhao Xiangjun. Kinematic model and tracking control for a trailed implement ［J］. Journal of Chinese Agricultural Mechanization， 2021， 42（4）： 128-133.

［15］狄桓宇， 張亞輝， 王博， 等. 自動駕駛橫向控制模型及方法研究綜述［J］. 重慶理工大學學報（自然科學）， 2021， 35（7）： 71-81.

Di Huanyu， Zhang Yahui， Wang Bo， et al. Review on the method and model of intelligent vehicle lateral control ［J］. Journal of Chongqing University of Technology （Natural Science）， 2021， 35（7）： 71-81.

［16］左帥， 劉成昊， 張笑， 等. 基于LQR的工程車輛自動駕駛路徑跟蹤技術研究［J］. 工程機械， 2022， 53（3）： 54-58， 10.

Zuo Shuai， Liu Chenghao， Zhang Xiao， et al. Research on automatic driving path tracking technology of engineering vehicles based on LQR ［J］. Construction Machinery and Equipment， 2022， 53 （03）： 54-58， 10.

［17］王鑫， 凌銘， 饒啟鵬， 等. 基于改進Stanley算法的無人車路徑跟蹤融合算法研究［J］. 汽車技術， 2022（7）： 25-31.

Wang Xin， Ling Ming， Rao Qipeng， et al. Research on fusion algorithm of unmanned vehicle path tracking based on improved Stanley algorithm ［J］. Automotive Technology， 2022（7）： 25-31.

［18］熊璐， 楊興， 卓桂榮， 等. 無人駕駛車輛的運動控制發展現狀綜述［J］. 機械工程學報， 2020， 56（10）： 127-143.

Xiong Lu， Yang Xing， Zhuo Guirong， et al. Review on motion control of autonomous vehicles ［J］. Journal of Mechanical Engineering， 2020， 56（10）： 127-143.

［19］楊菊花， 李文元， 陳光武， 等. 引入滑模觀測器的GPS/INS組合導航濾波方法［J］. 儀器儀表學報， 2019， 40（9）：78-86.

Yang Juhua， Li Wenyuan， Chen Guangwu， et al. GPS/INS integrated navigation filtering method based on sliding mode observer ［J］ Chinese Journal of Science Instrument， 2019， 40（9）： 78-86.

［20］孟秀云， 王語嫣. 一種SINS/GPS緊組合導航系統的改進自適應擴展卡爾曼濾波算法［J］. 北京理工大學學報， 2018， 38（6）： 625-630， 636.

Meng Xiuyun， Wang Yuyan. An improved adaptive extended Kalman filter algorithm of SINS/GPS tightly-coupled integrated navigation system ［J］. Transactions of Beijing Institute of Technology， 2018， 38（6）： 625-630， 636.